 М А О У С О Ш № Модуль и его приложения L/O/G/O www. themegallery. com 5
М А О У С О Ш № Модуль и его приложения L/O/G/O www. themegallery. com 5
 Содержание: Понятие модуля Свойства модуля 1°– 5° Свойства модуля 6°– 10° Геометрическая интерпретация модуля Примеры Решение уравнений вида |f(x)|= a Решение уравнений вида |f(x)|= g(x) Решение уравнений вида |f(x)| = |g(x)|
Содержание: Понятие модуля Свойства модуля 1°– 5° Свойства модуля 6°– 10° Геометрическая интерпретация модуля Примеры Решение уравнений вида |f(x)|= a Решение уравнений вида |f(x)|= g(x) Решение уравнений вида |f(x)| = |g(x)|
 Понятие модуля Абсолютной величиной (модулем) действительного числа а называется само число а, если оно неотрицательное, и число, противоположное а, если а – отрицательное. Пример:
Понятие модуля Абсолютной величиной (модулем) действительного числа а называется само число а, если оно неотрицательное, и число, противоположное а, если а – отрицательное. Пример:
 Свойства модуля
Свойства модуля
 Свойства модуля
Свойства модуля
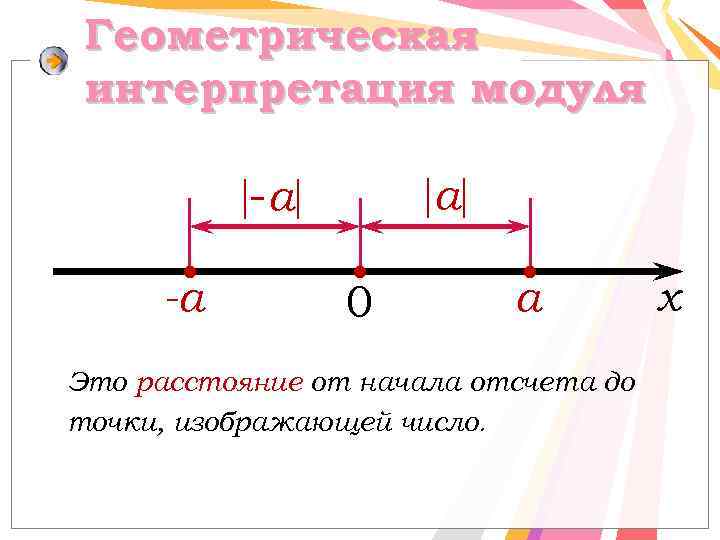 Геометрическая интерпретация модуля а -а -а 0 а Это расстояние от начала отсчета до точки, изображающей число. х
Геометрическая интерпретация модуля а -а -а 0 а Это расстояние от начала отсчета до точки, изображающей число. х
 Примеры Раскрыть модули: 1) 2) 3) 6) 7) 8) 4) 5) 9)
Примеры Раскрыть модули: 1) 2) 3) 6) 7) 8) 4) 5) 9)
 Решение уравнений вида f ( x) = a Пример: x – 8 = 5 ⇔ Ответ: 3; 13.
Решение уравнений вида f ( x) = a Пример: x – 8 = 5 ⇔ Ответ: 3; 13.
 Решение уравнений вида |f(x)|= a |2 x – 3|= 4 |5 x + 6|= 7 |9 – 3 x |= 6 |4 x + 2|= – 1 |8 – 2 x|= 0 |10 x + 3|= 16 |24 – 3 x|= 12 |2 x + 30|= 48 x 1 = 3, 5; x 1 = 0, 2; x 1 = 1; x Ø x=4 x 1 = 1, 3; x 1 = 12; x 1 = 9; x 2 = – 0, 5 x 2 = – 2, 6 x 2 = 5 x 2 = – 1, 9 x 2 = 4 x 2 = – 39
Решение уравнений вида |f(x)|= a |2 x – 3|= 4 |5 x + 6|= 7 |9 – 3 x |= 6 |4 x + 2|= – 1 |8 – 2 x|= 0 |10 x + 3|= 16 |24 – 3 x|= 12 |2 x + 30|= 48 x 1 = 3, 5; x 1 = 0, 2; x 1 = 1; x Ø x=4 x 1 = 1, 3; x 1 = 12; x 1 = 9; x 2 = – 0, 5 x 2 = – 2, 6 x 2 = 5 x 2 = – 1, 9 x 2 = 4 x 2 = – 39
 Решение уравнений вида f ( x) = g ( x) или
Решение уравнений вида f ( x) = g ( x) или
 Пример 3 х – 10 = х – 2 : ⇔ ⇔ Ответ: 3; 4. ⇔
Пример 3 х – 10 = х – 2 : ⇔ ⇔ Ответ: 3; 4. ⇔
 Решение уравнений вида f ( x) = g ( x) Пример: x – 2 = 3 – x ⇔ Ответ: 2, 5. ⇔
Решение уравнений вида f ( x) = g ( x) Пример: x – 2 = 3 – x ⇔ Ответ: 2, 5. ⇔
 Решить самостоятельно: 4 x – 1 = 2 х + 3 ⇔ ⇔ 1. Ответ: 2; – --3
Решить самостоятельно: 4 x – 1 = 2 х + 3 ⇔ ⇔ 1. Ответ: 2; – --3
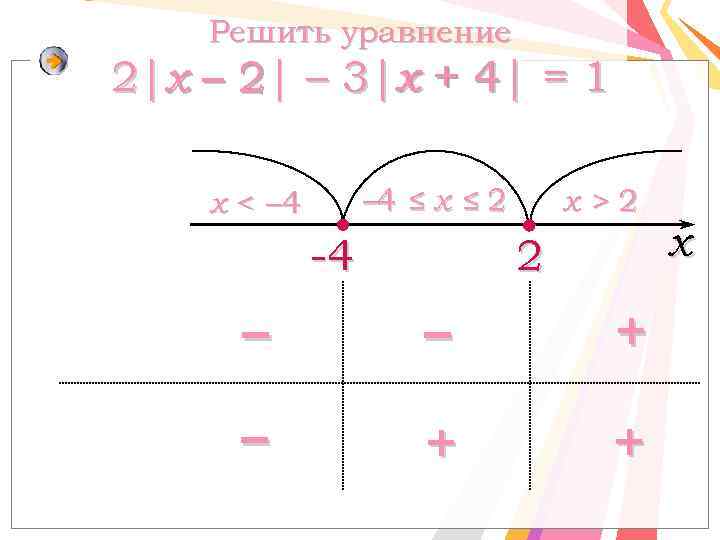 Решить уравнение 2|x – 2 – 3|x + 4 = 1 2| х 4| – 4 ≤ x ≤ 2 x < – 4 -4 x>2 2 – – + + х
Решить уравнение 2|x – 2 – 3|x + 4 = 1 2| х 4| – 4 ≤ x ≤ 2 x < – 4 -4 x>2 2 – – + + х
 Решить уравнение 2 x – 2 – 3 х + 4 = 1 ⇔ Ответ: – 15; – 1, 8.
Решить уравнение 2 x – 2 – 3 х + 4 = 1 ⇔ Ответ: – 15; – 1, 8.
 Примеры (решить самостоятельно) 1) x 2 + 3 x = 2(x + 1) 2) x – 6 = x 2 – 5 x + 9 3) 2 x + 8 – x – 5 = 12
Примеры (решить самостоятельно) 1) x 2 + 3 x = 2(x + 1) 2) x – 6 = x 2 – 5 x + 9 3) 2 x + 8 – x – 5 = 12