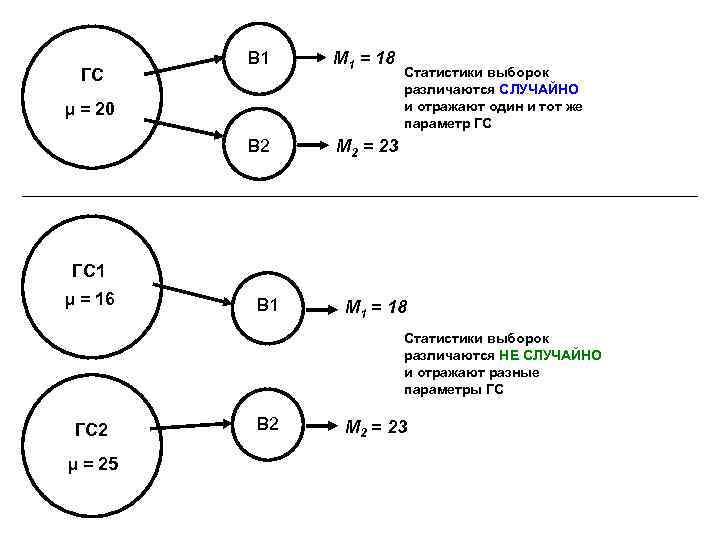
М 1 = 18 В 2 ГС В 1 М 2 = 23 μ = 20 Статистики выборок различаются СЛУЧАЙНО и отражают один и тот же параметр ГС ГС 1 μ = 16 В 1 М 1 = 18 Статистики выборок различаются НЕ СЛУЧАЙНО и отражают разные параметры ГС ГС 2 μ = 25 В 2 М 2 = 23
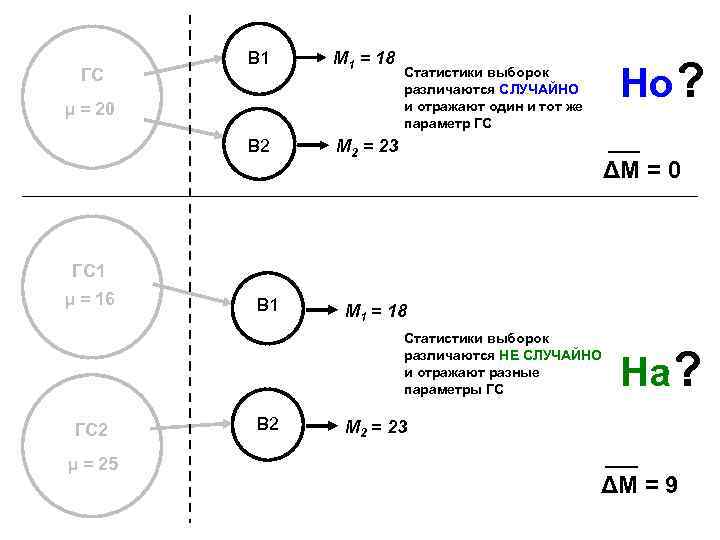М 1 = 18 В 2 ГС В 1 М 2 = 23 μ = 20 Но ? Статистики выборок различаются СЛУЧАЙНО и отражают один и тот же параметр ГС ΔM = 0 ГС 1 μ = 16 В 1 М 1 = 18 Статистики выборок различаются НЕ СЛУЧАЙНО и отражают разные параметры ГС ГС 2 μ = 25 В 2 На ? М 2 = 23 ΔM = 9
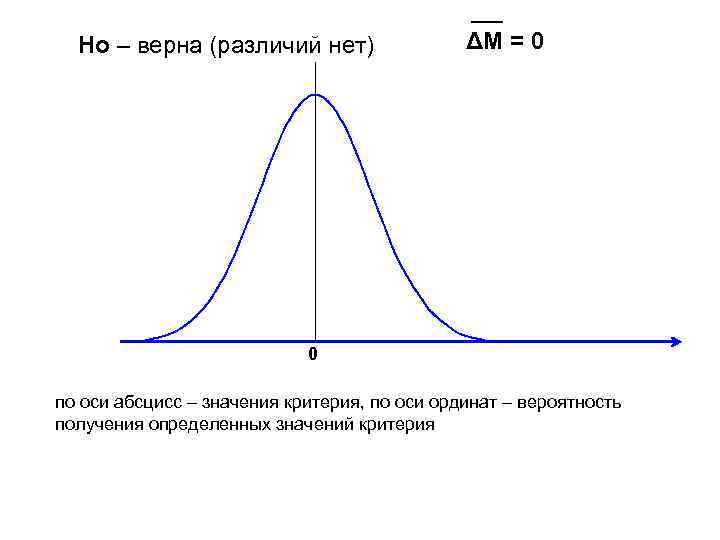Но – верна (различий нет) ΔM = 0 0 по оси абсцисс – значения критерия, по оси ординат – вероятность получения определенных значений критерия
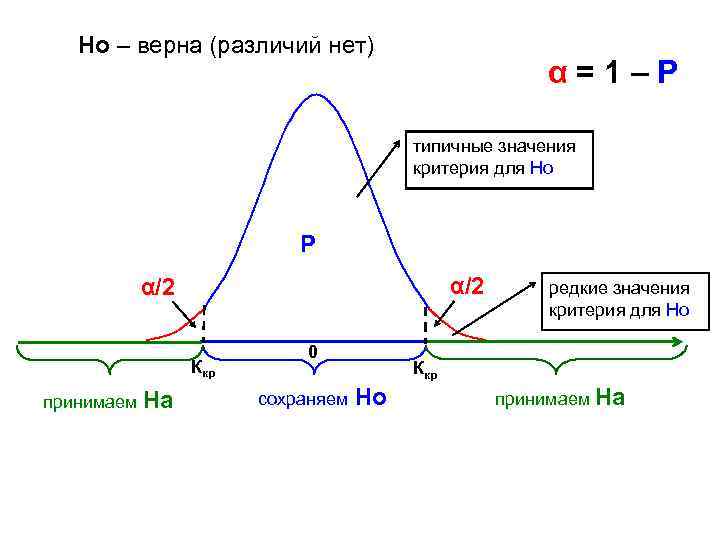Но – верна (различий нет) α=1–P типичные значения критерия для Но Р α/2 Ккр принимаем На 0 сохраняем редкие значения критерия для Но Ккр Но принимаем На
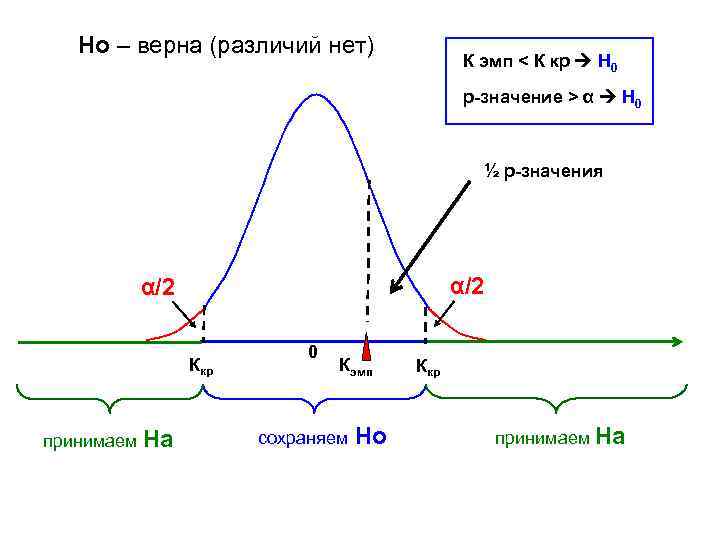Но – верна (различий нет) К эмп < К кр H 0 p-значение > α H 0 ½ p-значения α/2 Ккр принимаем На 0 Кэмп сохраняем Но Ккр принимаем На
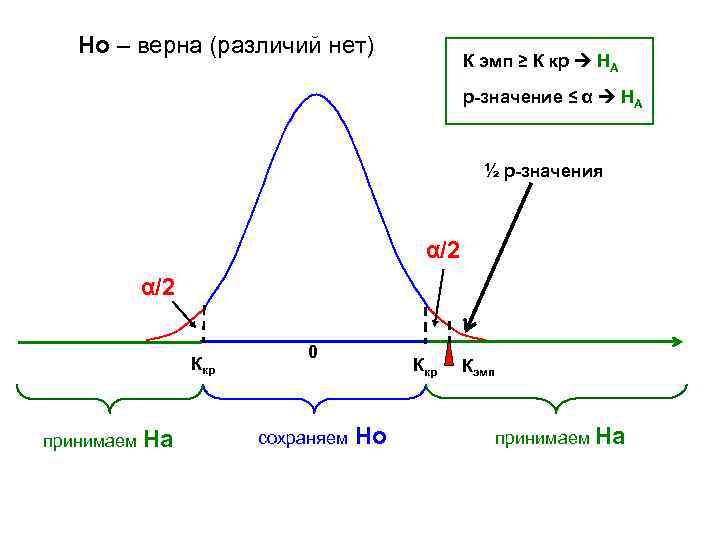Но – верна (различий нет) К эмп ≥ К кр HА p-значение ≤ α HА ½ p-значения α/2 Ккр принимаем На 0 сохраняем Ккр Но Кэмп принимаем На
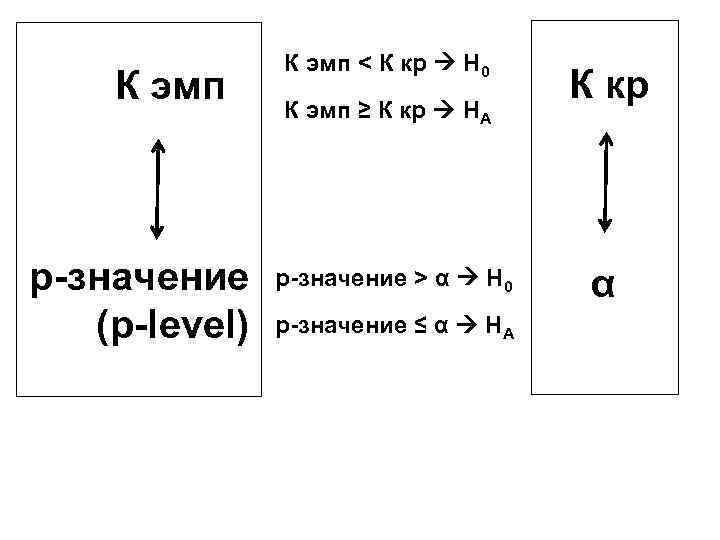К эмп p-значение (p-level) К эмп < К кр H 0 К эмп ≥ К кр HА p-значение > α H 0 p-значение ≤ α HА К кр α
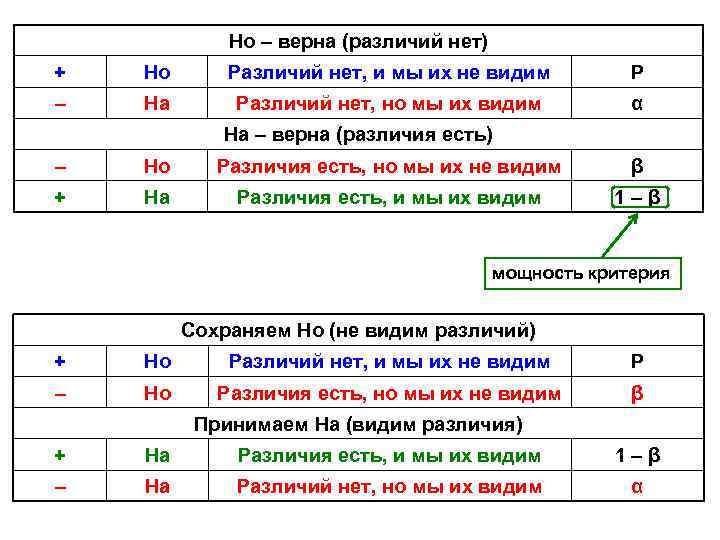Но – верна (различий нет) + Но Различий нет, и мы их не видим P – На Различий нет, но мы их видим α На – верна (различия есть) – Но Различия есть, но мы их не видим β + На Различия есть, и мы их видим 1–β мощность критерия Сохраняем Но (не видим различий) + Но Различий нет, и мы их не видим P – Но Различия есть, но мы их не видим β Принимаем На (видим различия) + На Различия есть, и мы их видим 1–β – На Различий нет, но мы их видим α
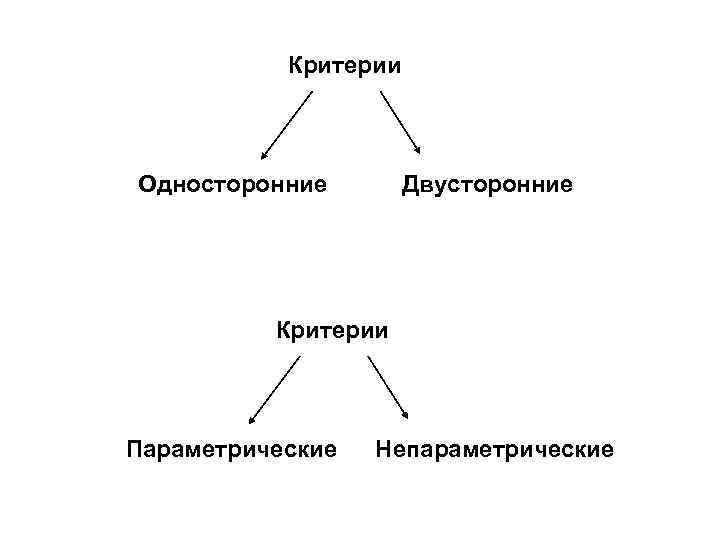Критерии Односторонние Двусторонние Критерии Параметрические Непараметрические
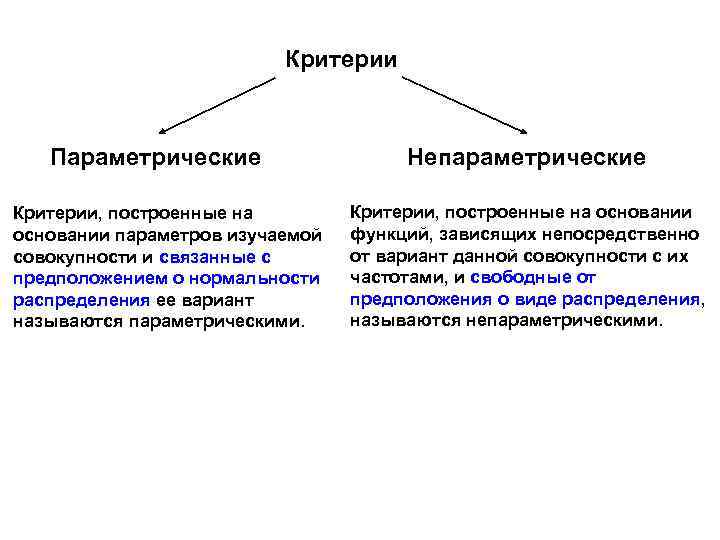Критерии Параметрические Критерии, построенные на основании параметров изучаемой совокупности и связанные с предположением о нормальности распределения ее вариант называются параметрическими. Непараметрические Критерии, построенные на основании функций, зависящих непосредственно от вариант данной совокупности с их частотами, и свободные от предположения о виде распределения, называются непараметрическими.
Сравнение долей (критерий Стьюдента) количественные и качественные признаки p 1 и p 2 – доли определенного значения в выборке 1 и 2 (в долях единицы) n 1 и n 2 – объемы выборок q 1 = 1 – p 1 q 2 = 1 – p 2 Ho: p 1 и p 2 различаются случайно (недостоверно) Hа: p 1 и p 2 различаются не случайно (достоверно) p-значение (tэмп, ν)
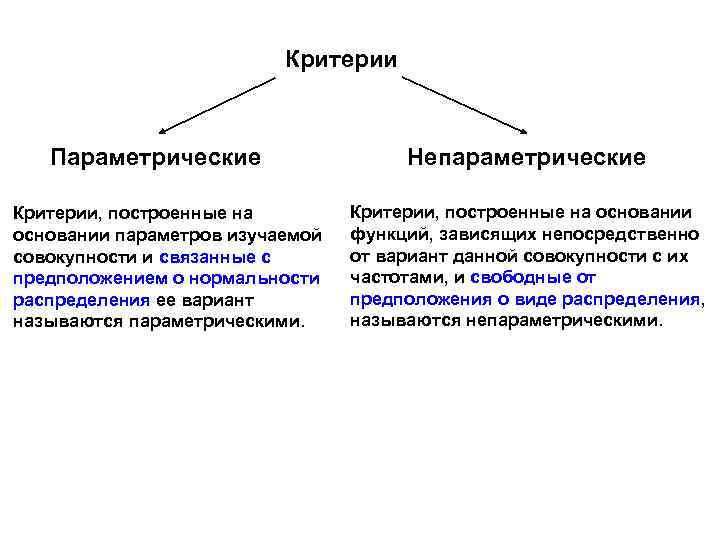Критерии Параметрические Критерии, построенные на основании параметров изучаемой совокупности и связанные с предположением о нормальности распределения ее вариант называются параметрическими. Непараметрические Критерии, построенные на основании функций, зависящих непосредственно от вариант данной совокупности с их частотами, и свободные от предположения о виде распределения, называются непараметрическими.
Анализ распределения (сравнение с нормальным распределением) Критерии: 1. Критерий χ2 Требует группировку ряда, число степеней свободы – df = k – 3) Ограничения – большая выборка (50), теоретические частоты > 5. 2. Критерий λ (Колмогорова-Смирнова) и/или Lilliefort’s тест Нет ограничений по объему выборки. Наименее чувствительный тест. 3. Тест Шапиро-Уилка Нет ограничений по объему выборки (n > 3). Наиболее мощный тест. Оптимальный способ оценки соответствия нормальному распределению для выборок любого объема.
Анализ распределений в Statistica 1. Statistics Basic statistic/Tables Descriptive statistics Normality Расчет нормальных частот, тесты Колмогоров-Смирнов, Лиллифорт, Шапиро-Уилк. Недостатки – сложно управлять группировкой ряда, не рисует иллюстрацию к тесту Шапиро-Уилка. 2. Statistics Basic statistic/Tables Frequency tables a) Options Normal expected frequencies – расчет нормальных частот b) Advansed – расширенные возможности группировки ряда c) Normality – тесты Колмогоров-Смирнов, Лиллифорт, Шапиро-Уилк d) Descr. – графики в т. ч. кумуляты нормального распределения 3. Statistics Distributions fitting Возможность сравнения эмпирического распределения с разными моделями. Тесты χ2 (Chi-Square test), Колмогоров-Смирнов Недостатки – сложно управлять группировкой ряда. 4. Graphs 2 D Graphs Normal Probability Plots… Quik График кумуляты нормального распределения и тест Шапиро-Уилка. Оптимальный способ оценки нормального распределения