 лы у рм о о Ф ог н ой та в д ен ум рг а
лы у рм о о Ф ог н ой та в д ен ум рг а
 Формула синуса двойного аргумента В формуле синуса суммы двух аргументов: sin(α + β) = sinα cosβ + cosα sinβ замените β на α: sin(α + α) = sinα cos α + sinα cosα получится формула синуса двойного аргумента.
Формула синуса двойного аргумента В формуле синуса суммы двух аргументов: sin(α + β) = sinα cosβ + cosα sinβ замените β на α: sin(α + α) = sinα cos α + sinα cosα получится формула синуса двойного аргумента.
 Формула косинуса двойного аргумента В формуле косинуса суммы двух аргументов: cos(α + β) = cosα cosβ − sinα sinβ замените β на α: cos(α + α) = cosα cos α − sinα получится формула косинуса двойного аргумента.
Формула косинуса двойного аргумента В формуле косинуса суммы двух аргументов: cos(α + β) = cosα cosβ − sinα sinβ замените β на α: cos(α + α) = cosα cos α − sinα получится формула косинуса двойного аргумента.
 Другие формулы косинуса двойного аргумента В формуле косинуса двойного аргумента заменим cos 2α: cos 2α = 1 − sin 2α получим: cos 2α = 1 − sin 2α = 1 − 2 sin 2α cos 2α = 1 − 2 sin 2α
Другие формулы косинуса двойного аргумента В формуле косинуса двойного аргумента заменим cos 2α: cos 2α = 1 − sin 2α получим: cos 2α = 1 − sin 2α = 1 − 2 sin 2α cos 2α = 1 − 2 sin 2α
 Другие формулы косинуса двойного аргумента В формуле косинуса двойного аргумента заменим sin 2α : sin 2α = 1 − cos 2α получим: cos 2α = cos 2α − 1 + cos 2α = 2 cos 2α − 1
Другие формулы косинуса двойного аргумента В формуле косинуса двойного аргумента заменим sin 2α : sin 2α = 1 − cos 2α получим: cos 2α = cos 2α − 1 + cos 2α = 2 cos 2α − 1
 Полезные равенства: cos 2α = 1 − 2 sin 2α тогда 2 sin 2α = 1 − cos 2α = 2 cos 2α − 1 2 cos 2α = 1 + cos 2α тогда
Полезные равенства: cos 2α = 1 − 2 sin 2α тогда 2 sin 2α = 1 − cos 2α = 2 cos 2α − 1 2 cos 2α = 1 + cos 2α тогда
 Формула тангенса двойного аргумента Из формулы тангенса суммы двух аргументов, заменив β на α, получить формулу тангенса двойного аргумента. получится формула тангенса двойного аргумента.
Формула тангенса двойного аргумента Из формулы тангенса суммы двух аргументов, заменив β на α, получить формулу тангенса двойного аргумента. получится формула тангенса двойного аргумента.
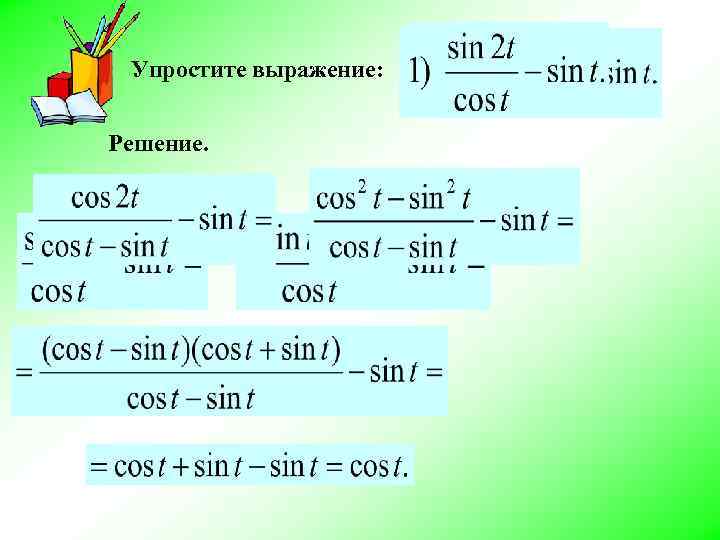 Упростите выражение: Решение.
Упростите выражение: Решение.
 Упростите выражение: Решение.
Упростите выражение: Решение.
 Вычислите: Ответ: 0, 5 Ответ: 1, 5
Вычислите: Ответ: 0, 5 Ответ: 1, 5
 Вычислите: Ответ: − 1
Вычислите: Ответ: − 1
 Вычислите самостоятельно: Ответ:
Вычислите самостоятельно: Ответ:
 Решите уравнение Решение. Ответ:
Решите уравнение Решение. Ответ:
 Формулы тригонометрии Плакат по тригонометрии (1 часть)
Формулы тригонометрии Плакат по тригонометрии (1 часть)
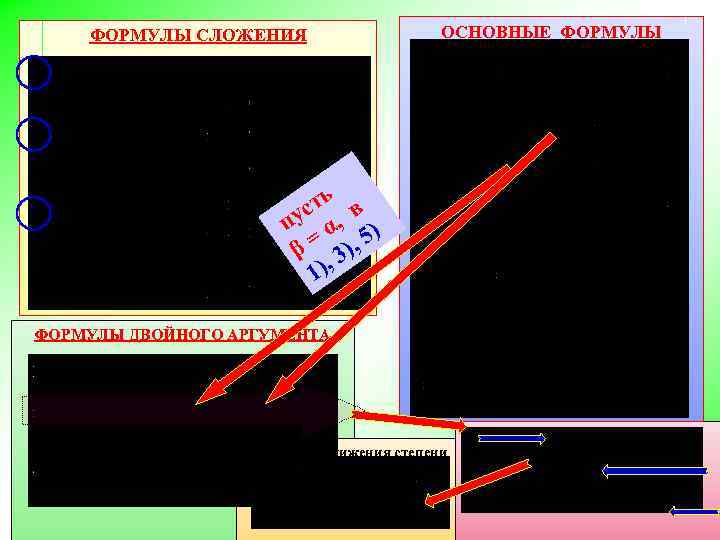 ФОРМУЛЫ СЛОЖЕНИЯ ОСНОВНЫЕ ФОРМУЛЫ ть в с пу α, ) 5 β = 3), 1), ФОРМУЛЫ ДВОЙНОГО АРГУМЕНТА Формулы понижения степени
ФОРМУЛЫ СЛОЖЕНИЯ ОСНОВНЫЕ ФОРМУЛЫ ть в с пу α, ) 5 β = 3), 1), ФОРМУЛЫ ДВОЙНОГО АРГУМЕНТА Формулы понижения степени