Лукьянова Е А Медицинская информатика Теория вероятностей Случайные

Лукьянова Е. А. Медицинская информатика Теория вероятностей Случайные величины 2011

Случайные величины Случайной называется величина, которая в результате опыта может принять то или иное возможное значение, неизвестное заранее, но обязательно одно. (с. в. X, Y, Z; знач. с. в. x, y, z) Примеры случайных величин l Число мальчиков, родившихся в течение суток в определенном городе. l Значение температуры измерении. l Число выпавших бросании монеты. “гербов” при l При однократном выпавших очков бросании кости при неоднократном пятикратном количество

Случайные величины Различают случайные величины следующих типов: Дискретные и непрерывные l Дискретной случайной величиной называют такую случайную величину, множество возможных значений которой либо конечное, либо бесконечное, но счетное. l Непрерывной случайной величиной называют такую случайную величину, которая может принять любое значение из некоторого конечного или бесконечного интервала.

Закон распределения случайной величины Законом распределения случайной величины называется правило, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может быть представлен в • Табличном • Аналитическом • Графическом виде

Дискретные случайные величины Простейшей формой задания закона дискретной случайной величины является таблица, в которой перечислены возможные значения случайных величин (упорядоченные по возрастающей) и соответствующие им вероятности. Пусть случайная величина X может принять одно из n возможных значений x 1, …, xn, с вероятностью p 1, …, pn соответственно Тогда закон распределения случайной величины X можно записать в виде таблицы X x 1 x 2 … xn P(X) p 1 p 2 … pn где х1<х2<…<хn.

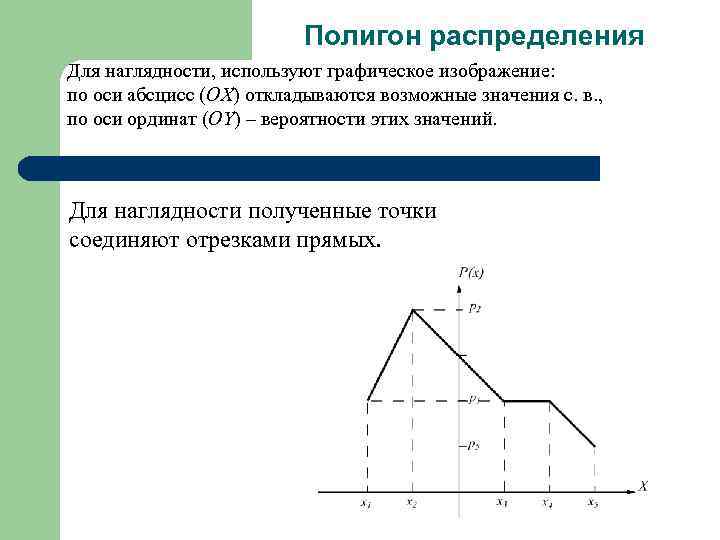Полигон распределения Для наглядности, используют графическое изображение: по оси абсцисс (ОХ) откладываются возможные значения с. в. , по оси ординат (ОY) – вероятности этих значений. Для наглядности полученные точки соединяют отрезками прямых.

Функция распределения вероятностей случайной величины Функцией распределения вероятностей случайной величины Х называется функция F(x), задающая вероятность того, что случайная величина Х принимает значения меньше х, т. е. F(x) = P(X < x). Свойства функции распределения : l Функция F(x) есть неубывающая функция своего аргумента, т. е. F(x 2) F(x 1) при х2 > x 1. l На минуc бесконечности функция F(x) = 0, F(- ) = 0 l На плюс бесконечности функция F(x) = 1, F(+ ) = 1 Для дискретных случайных величин: Р(Х<х) = Р(Х=х1)+. . . +Р(Х=хi)= (неравенство под знаком суммы означает, что суммирование касается всех тех значений хi, величина которых меньше х. )

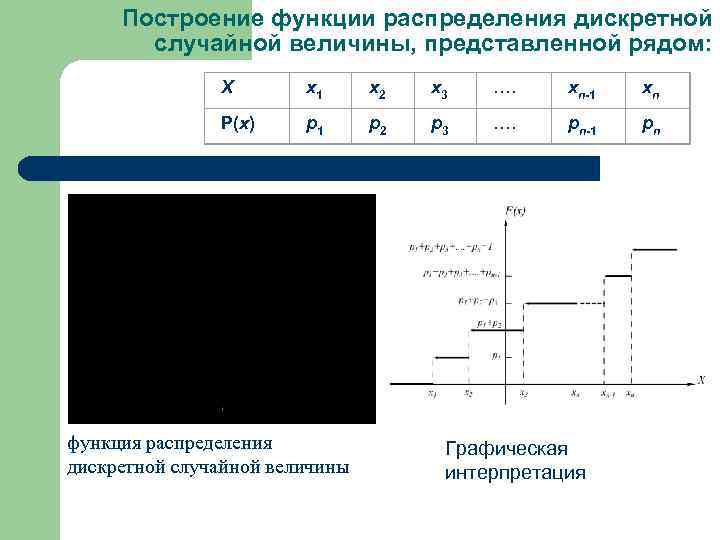Построение функции распределения дискретной случайной величины, представленной рядом: Х x 1 x 2 x 3 …. xn-1 xn P(x) p 1 p 2 p 3 …. pn-1 pn функция распределения дискретной случайной величины Графическая интерпретация

Пример Эксперимент: подбрасывают монету два раза, случайная величина X – это “число выпадения Герба при двух бросках монеты”. Надо построить вариационный ряд, полигон и функцию распределения X x 1 x 2 x 3 P p 1 p 2 p 3 X 0 1 2 P 0, 25

Плотность распределения непрерывной случайной величины Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения: f(x) = F (x). Свойства плотности распределения вероятностей: • Плотность распределения – неотрицательная функция, т. е. f(x) 0 x R. • Интеграл от плотности распределения в пределах от - до + = 1 • Плотность и функция распределения связаны между собой соотношением

Расчет вероятности Вероятность того, что случайная величина примет значение, принадлежащее заданному интервалу (а, b), зная либо плотность f(x), либо функцию F(x). Если известна функция распределения F(x), то вероятность равна Р(a

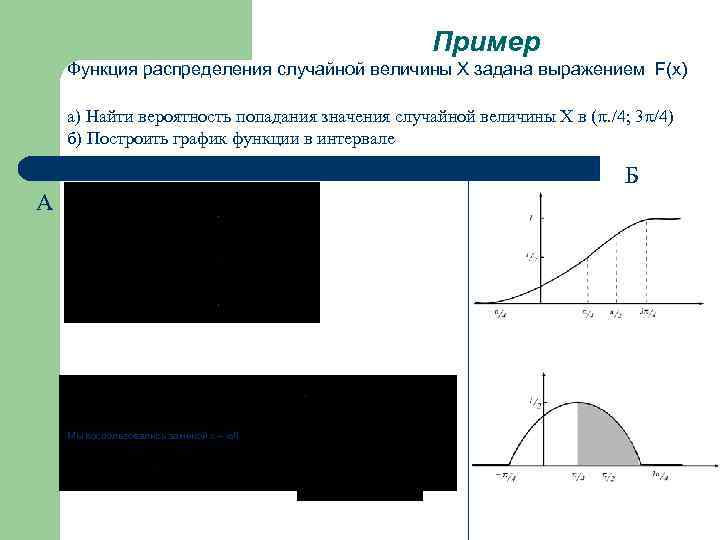Пример Функция распределения случайной величины Х задана выражением F(x) а) Найти вероятность попадания значения случайной величины Х в (. /4; 3 /4) б) Построить график функции в интервале Б А Мы воспользовались заменой x /4