LSP 120 Exponential Modeling What Makes It

LSP 120 Exponential Modeling

What Makes It Exponential? Linear relationship – where a fixed change in x increases or decreases y by a fixed amount n Exponential relationship – for a fixed change in x, there is a fixed percent change in y n

Exponential, Linear, or Neither? x 0 1 2 3 y 192 96 48 24 Percent change no formula here =(B 3 -B 2)/B 2 Apply =(B 3 -B 2)/B 2. If the column is constant, then the relationship is exponential. x 0 1 2 3 y 192 96 48 24 Percent change -50% Note: Answer was -. 5 but we converted these cells to % by clicking on the % icon on the toolbar

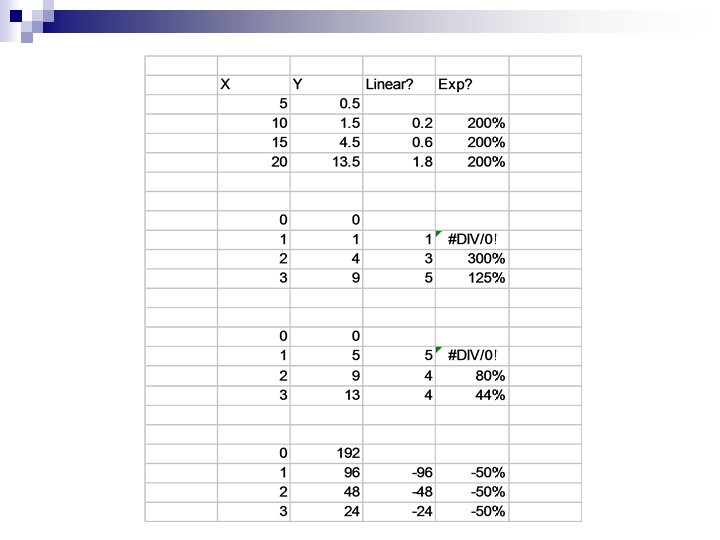
Linear, Exponential or Neither? Is each of these linear, exponential, or neither? x 5 10 15 20 y 0. 5 1. 5 4. 5 13. 5 x 0 1 2 3 y 0 1 4 9 x 0 1 2 3 y 0 5 9 13 Recall: to determine if it is linear: =(B 3 -B 2)/(A 3 -A 2) To determine if it is exponential: =(B 3 -B 2)/B 2 x 0 1 2 3 y 192 96 48 24

General Equation n As with linear, there is a general equation for an exponential function y = A * (1 + p)x where A is the initial value of y when x = 0 p is the percent change (written as a decimal) x is the input variable (very often time) n The equation for the previous example is y = 192 * (1 + (-0. 5))x, or y = 192 *. 5 x

Exponential Growth If the percentage change p is greater than 0, then we call the relationship exponential growth n If the percentage change p is less than 0, we call the relationship exponential decay n Many exponentials grow (or decrease) very rapidly eventually, but they also can be very, very flat, sometimes deceptively so. n

Exponential Growth If a quantity grows by a fixed percentage change, it grows exponentially n Say a quantity grows by p% each year. After one year, A will become A + Ap, or A*(1+p) n After the second year, you multiply again by 1+p, or A*(1+p)2 n After n years, it is A*(1+p)n (look familiar? ) n

Exponential Relationships n For example, the US population is growing by about 0. 8% each year. In 2000, the population was 282 million. A Year B Population by adding percent C Population by multiplying by growth factor (preferred form) 2000 2001 2002 2003 282 =B 2+B 2*0. 008 282 =C 2*(1+. 008)

Exponential Relationships n What if a country’s population was decreasing by 0. 2% per year? A Year B Population by adding percent C Population by multiplying by growth factor (preferred form) 2000 2001 2002 2003 344 =B 2 -B 2*0. 002 344 =C 2*(1+(-. 002))

A Very Common Exponential Growth Every time you buy something you pay sales tax (let’s say its 8. 5%) n The item you purchase is $39. 00 n Total price = 39 * (1+0. 085)1 n Total price = 42. 315, or $42. 32 n

Another Example A bacteria population is at 100 and is growing by 5% per minute n How many bacteria cells are present after one hour (60 minutes)? n You could solve it using a spreadsheet… n

X minutes Y population 0 100 1 =B 2 * (1 +. 05) 2 3 =A 5+1 Let’s make this chart in Excel.

Another Example n Or you could skip the spreadsheet and solve it mathematically Population = 100 * (1+. 05)60 Note: 60 is an exponent in the above equation (but not in the spreadsheet)

What If? What if you knew the final population and wanted to figure out how long it would take to arrive at this answer? For example, when will the Y population be = 1000? n You could look at the spreadsheet, but… n You might have to make a guess n Let’s not guess, let’s use math n

What If? n Let’s use logarithms 1000 = 100(1+. 05)X 10 = 1. 05 X log(10) = log(1. 05)X log(10) = x * log(1. 05) 1 = x * 0. 021 x = 1/0. 021 x = 47. 61

Is Exponential Modeling Useful? Populations tend to grow exponentially n When an object cools, the temperature decreases exponentially towards the ambient temp n Radioactive substances (both good and bad) decay exponentially n Money accumulating in a bank at a fixed rate of interest increases exponentially n Viruses and even rumors spread exponentially n

Radioisotope Dating What is radioactivity? n What is it good for? n What is the connection with exponential growth / decay? n

Radioisotope Dating n So what is radioisotope dating? ¨ The radioisotope age of a specimen is obtained from a calculation of the time that would be required for unstable parent atoms [P] to spontaneously convert to daughter atoms [D] in sufficient amount to account for the present D/P ratio in the specimen. n Unstable Carbon, Uranium, Potassium often used (Carbon 14 (12), Uranium 238, Potassium 40(39))

Example The Dead Sea Scrolls have about 78% of the normally occurring amount of Carbon 14 in them n Carbon 14 decays at a rate of about 1. 202% every 100 years n Let’s create a spreadsheet which calculates this exponential delay n

Example Years after Death 0 100 200 ? Let’s go to the lab. % Carbon Remaining 100 =B 2 * (1 - 0. 01202) Stop when % Carbon Remaining = 78%