Loop Shaping SISO case 0 db António Pascoal

Loop Shaping (SISO case) 0 db António Pascoal 2011 Instituto Superior Tecnico antonio@isr. ist. utl. pt

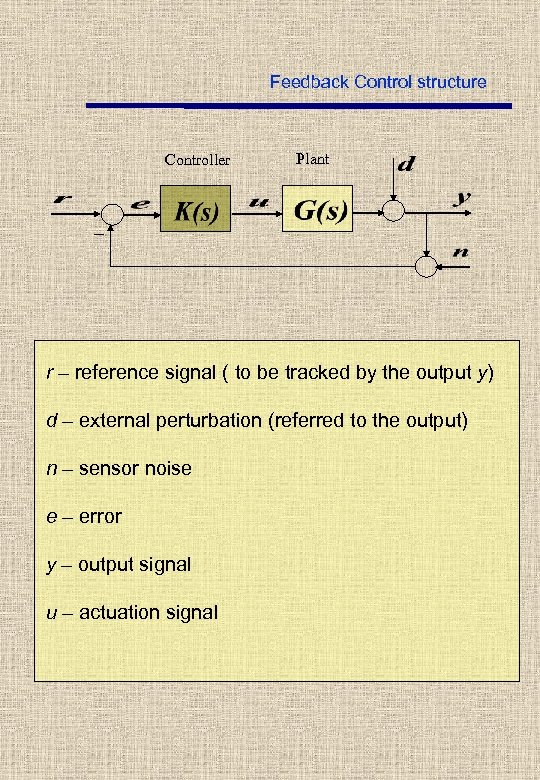
Feedback Control structure Controller Plant _ r – reference signal ( to be tracked by the output y) d – external perturbation (referred to the output) n – sensor noise e – error y – output signal u – actuation signal

Key objectives Design the controller K(s) such that i) K(s) stabilizes G(s) ii) The output y follows the reference signals r. iii) The system reduces the effect of external disturbance d and noise n on the output y. iv) The actuation signal u is not driven beyond limits imposed by saturation values and bandwith of the plant´s actuator. v) The system meets stability and performance requirements in the face of plant parameter uncertainty and unmodeled dynamics (robust stability and robust performance).

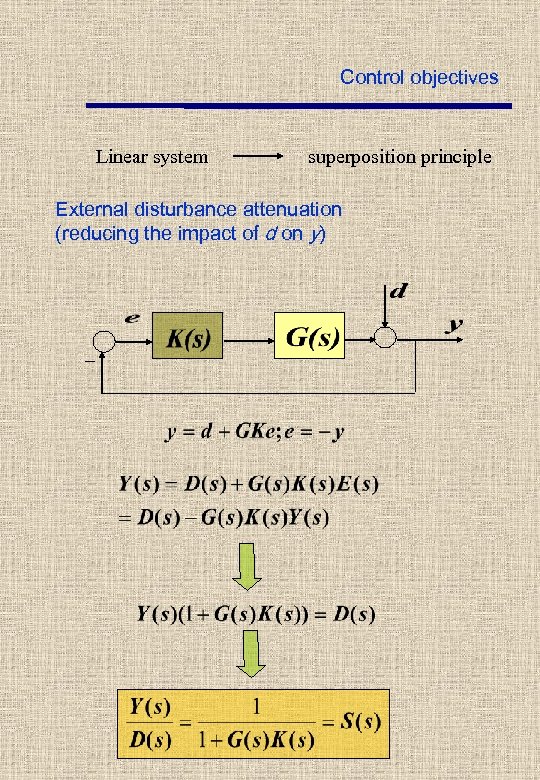
Control objectives Linear system superposition principle External disturbance attenuation (reducing the impact of d on y) _

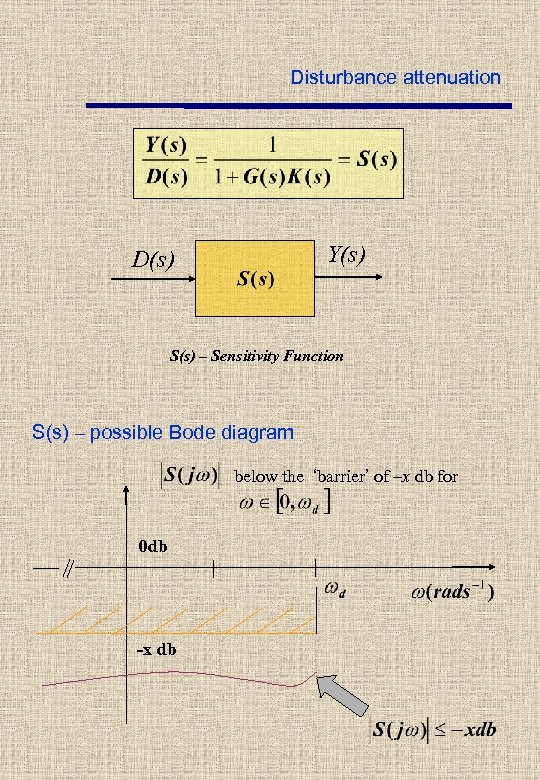
Disturbance attenuation Y(s) D(s) S(s) – Sensitivity Function S(s) – possible Bode diagram below the ‘barrier’ of –x db for 0 db -x db

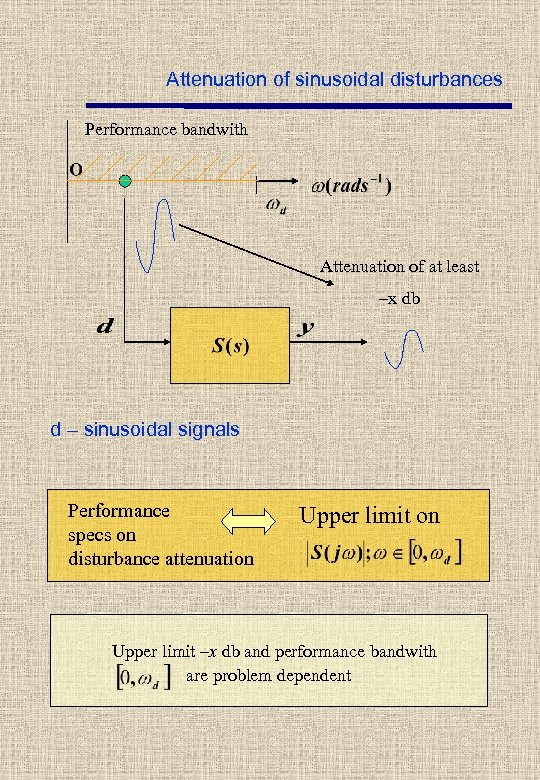
Attenuation of sinusoidal disturbances Performance bandwith Attenuation of at least –x db d – sinusoidal signals Performance specs on disturbance attenuation Upper limit –x db and performance bandwith are problem dependent

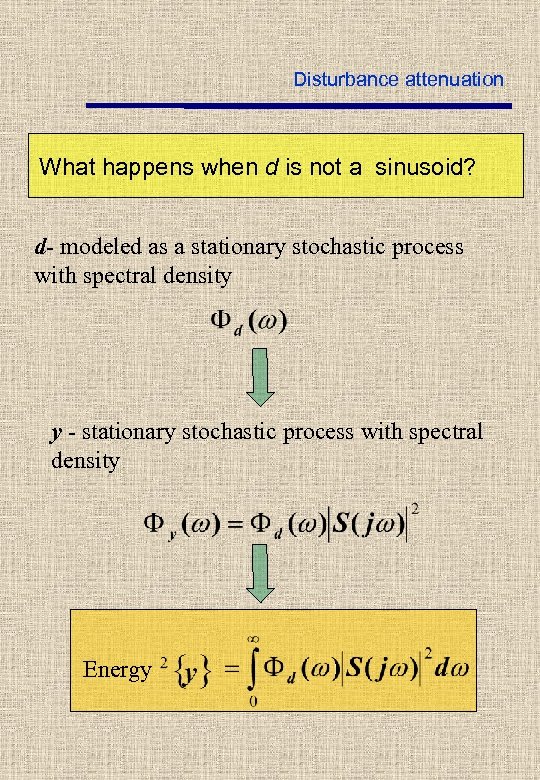
Disturbance attenuation What happens when d is not a sinusoid? d- modeled as a stationary stochastic process with spectral density y - stationary stochastic process with spectral density Energy

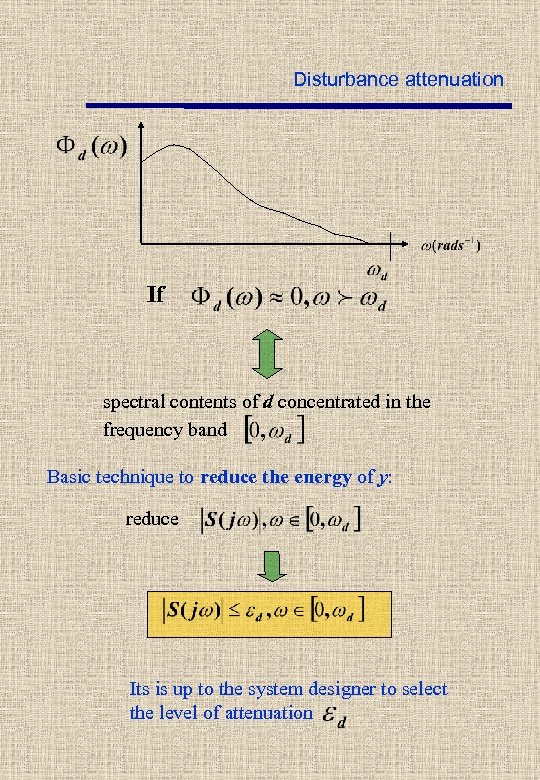
Disturbance attenuation If spectral contents of d concentrated in the frequency band Basic technique to reduce the energy of y: reduce Its is up to the system designer to select the level of attenuation

Disturbance attenuation: constraints on the Loop Gain GK If Disturbace attenuation

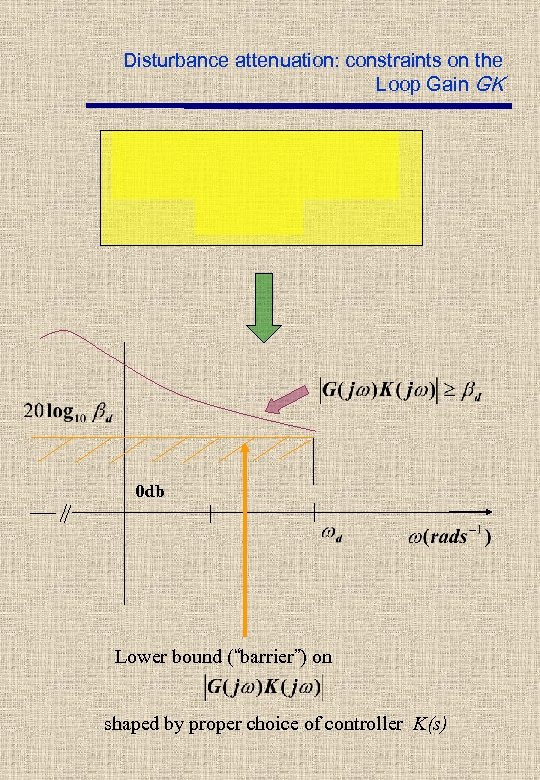
Disturbance attenuation: constraints on the Loop Gain GK 0 db Lower bound (“barrier”) on shaped by proper choice of controller K(s)

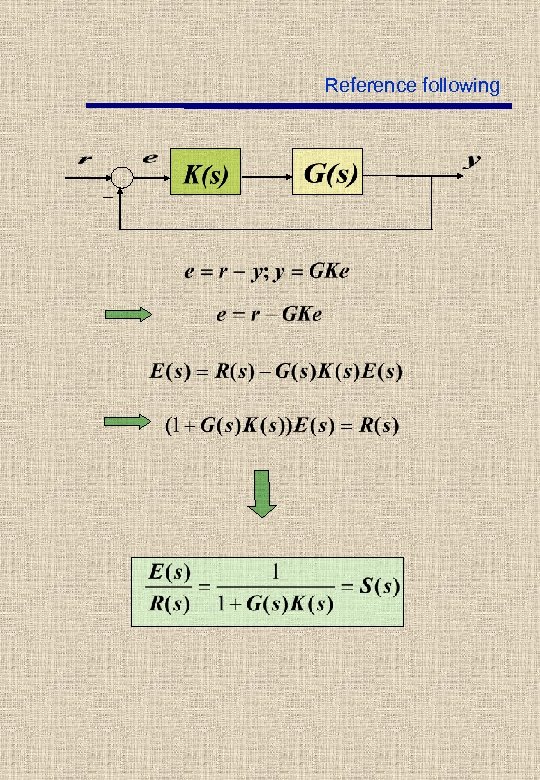
Reference following _

Reference following r- modeled as a stationary stochastic process with spectral density e - stationary stochastic process with spectral density Energia

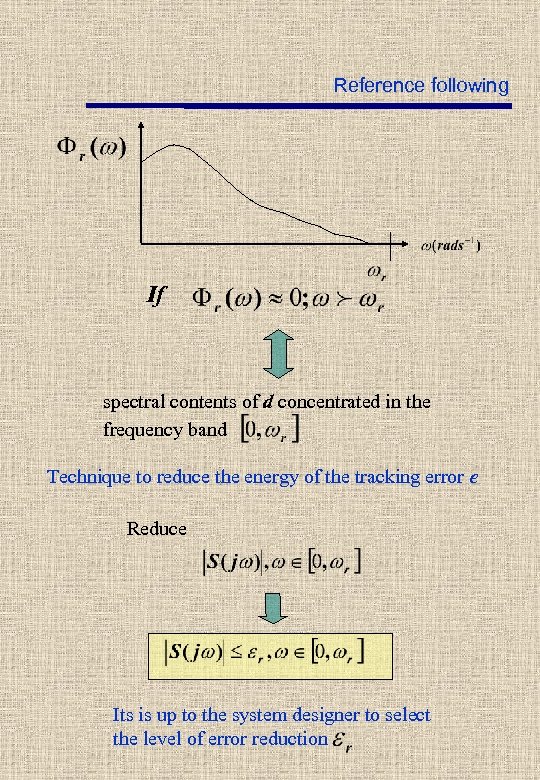
Reference following If spectral contents of d concentrated in the frequency band Technique to reduce the energy of the tracking error e Reduce Its is up to the system designer to select the level of error reduction

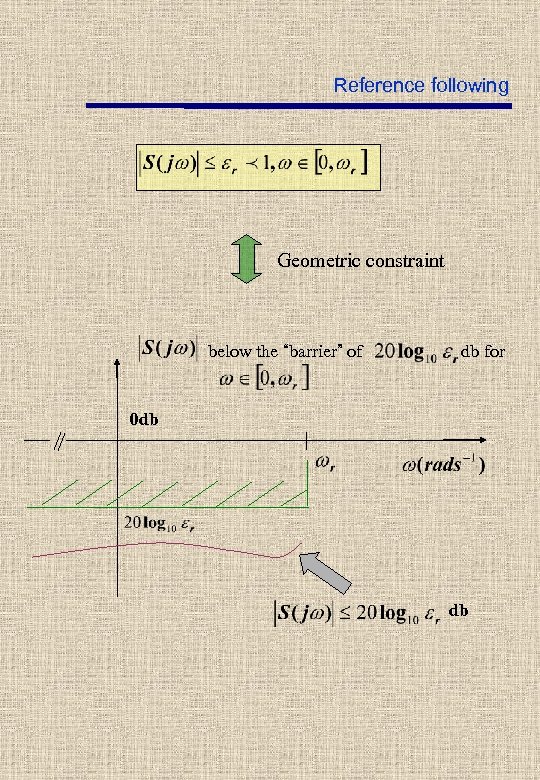
Reference following Geometric constraint below the “barrier” of db for 0 db db

Reference following: constraints on the Loop Gain GK If reference following:

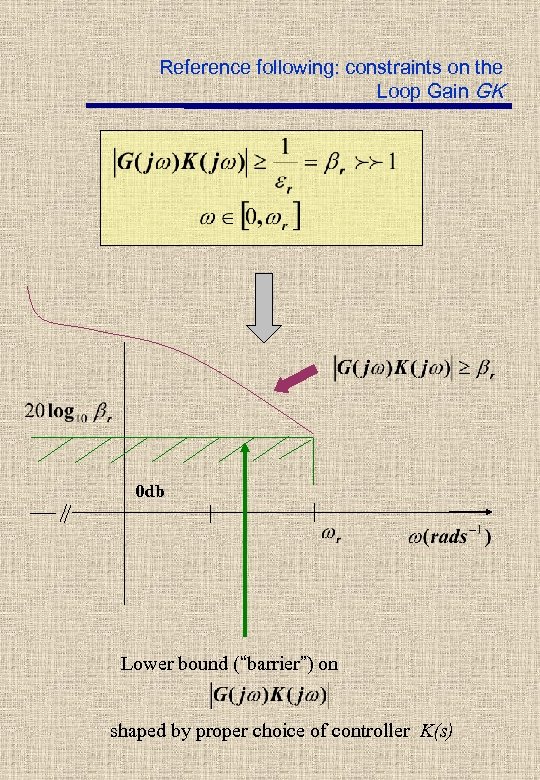
Reference following: constraints on the Loop Gain GK 0 db Lower bound (“barrier”) on shaped by proper choice of controller K(s)

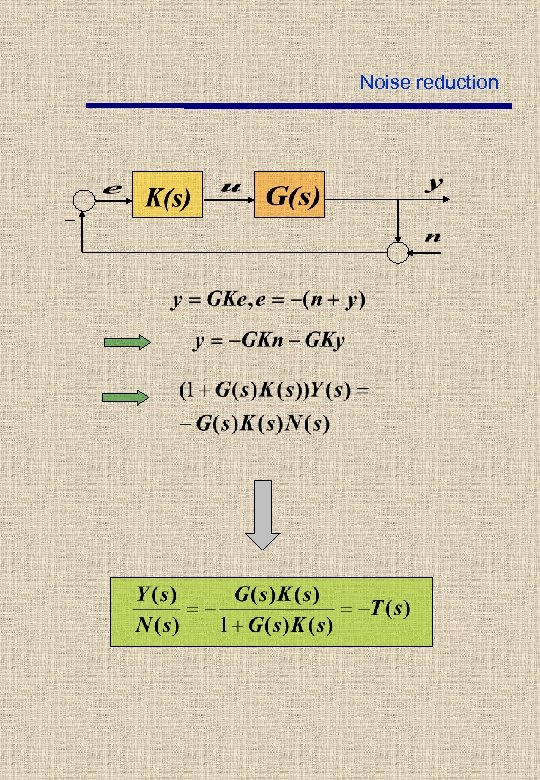
Noise reduction _

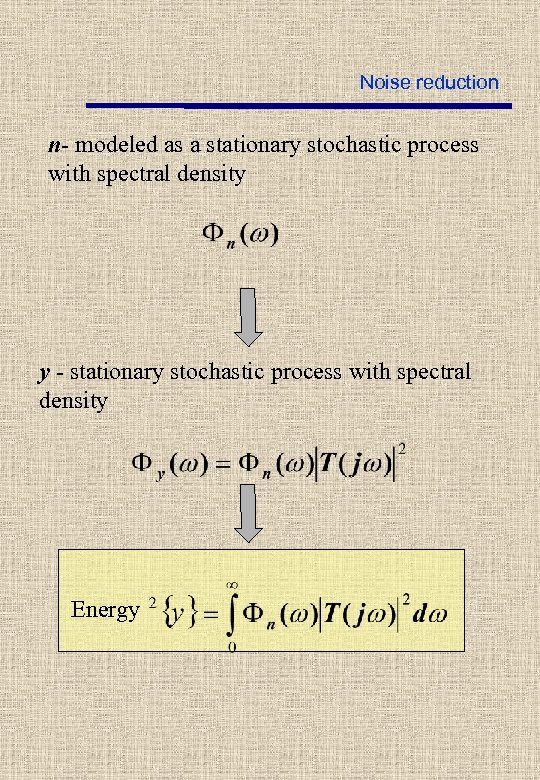
Noise reduction n- modeled as a stationary stochastic process with spectral density y - stationary stochastic process with spectral density Energy

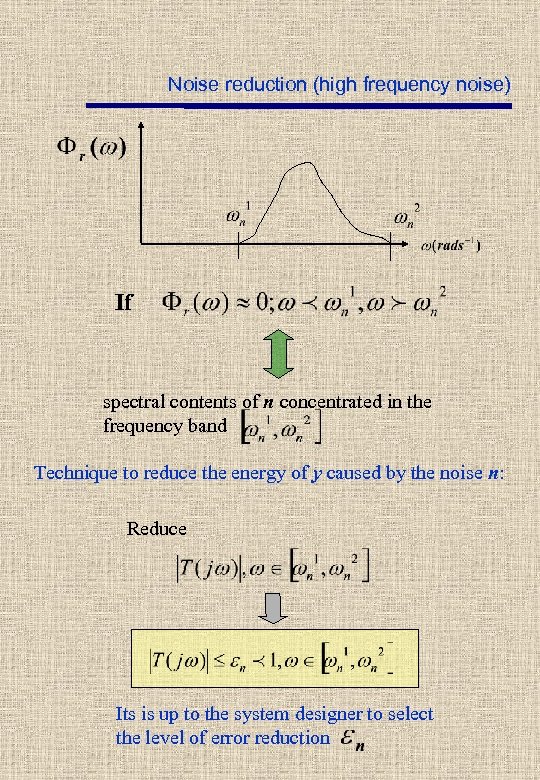
Noise reduction (high frequency noise) If spectral contents of n concentrated in the frequency band Technique to reduce the energy of y caused by the noise n: Reduce Its is up to the system designer to select the level of error reduction

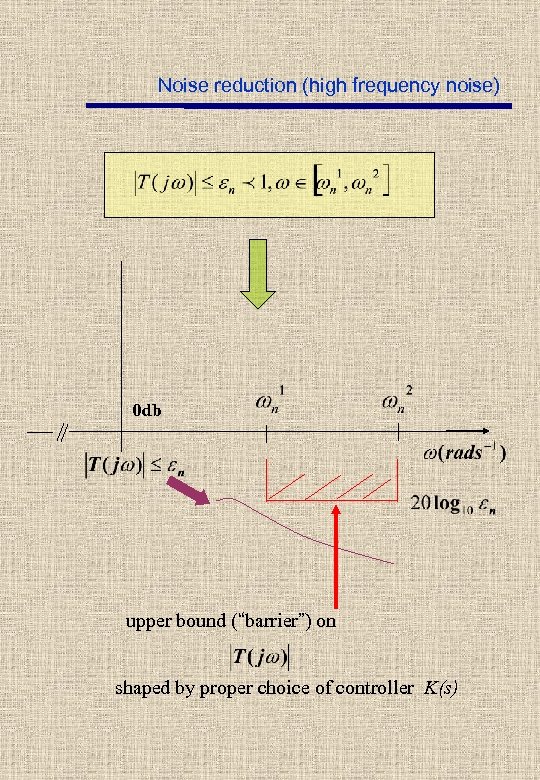
Noise reduction (high frequency noise) 0 db upper bound (“barrier”) on shaped by proper choice of controller K(s)

Noise reduction: constraints on the Loop Gain GK If noise reduction

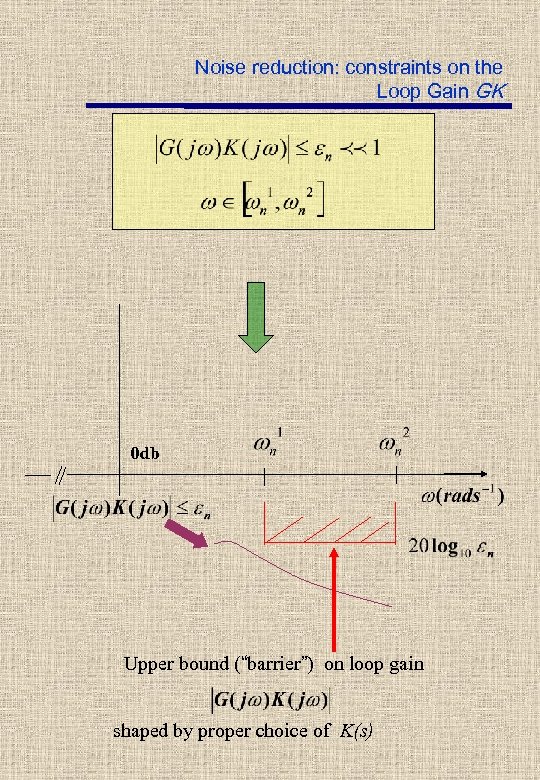
Noise reduction: constraints on the Loop Gain GK 0 db Upper bound (“barrier”) on loop gain shaped by proper choice of K(s)

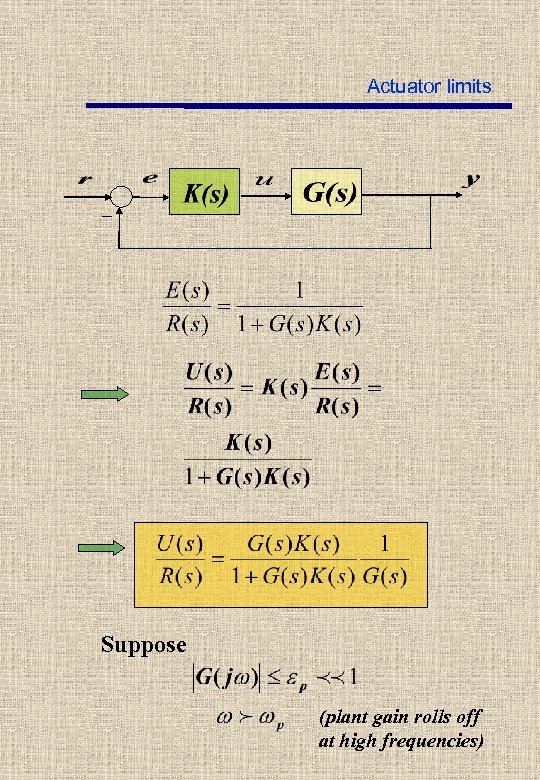
Actuator limits _ Suppose (plant gain rolls off at high frequencies)

Actuator limits Suppose Actuation signals too high unless the loop gain starts rolling off at frequencies below Golden rule: never try to make the closed loop bandwidth extend well above the region where the plant gain starts to roll off below 0 db.

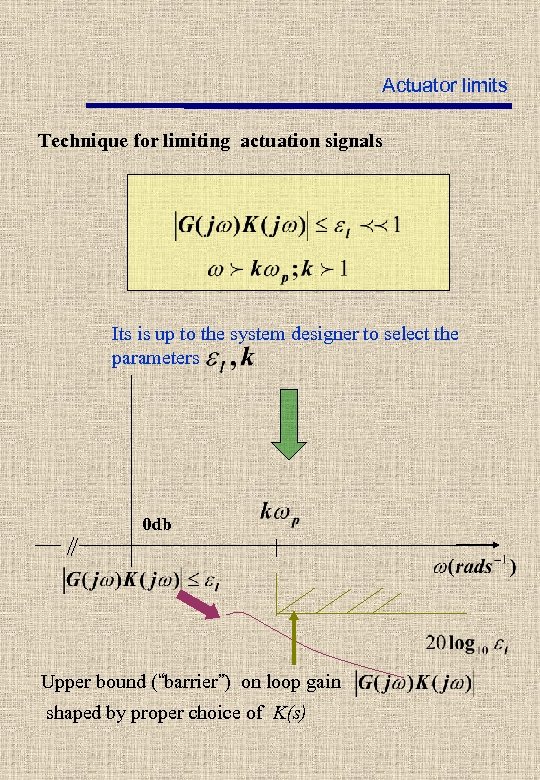
Actuator limits Technique for limiting actuation signals Its is up to the system designer to select the parameters 0 db Upper bound (“barrier”) on loop gain shaped by proper choice of K(s)

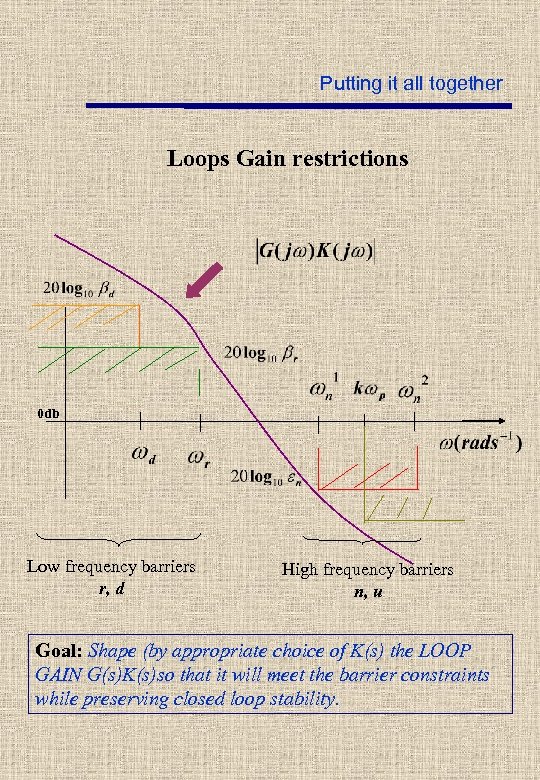
Putting it all together Loops Gain restrictions 0 db Low frequency barriers r, d High frequency barriers n, u Goal: Shape (by appropriate choice of K(s) the LOOP GAIN G(s)K(s)so that it will meet the barrier constraints while preserving closed loop stability.

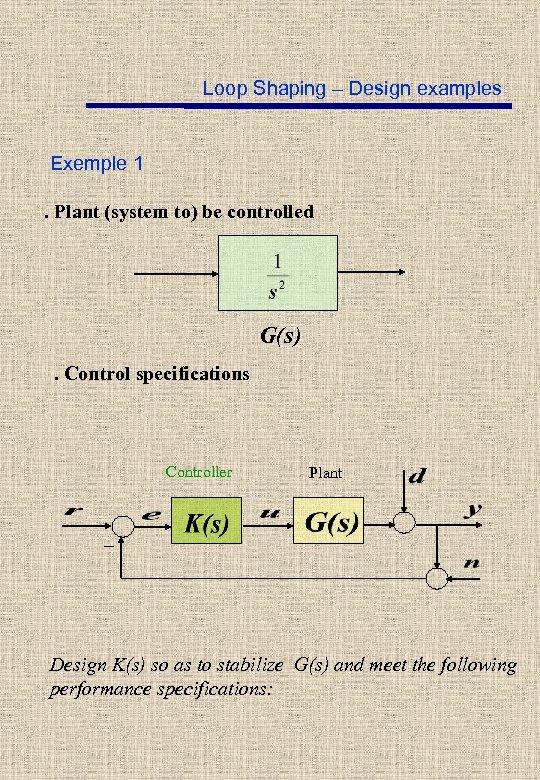
Loop Shaping – Design examples Exemple 1. Plant (system to) be controlled G(s). Control specifications Controller Plant _ Design K(s) so as to stabilize G(s) and meet the following performance specifications:

Loop Shaping – Design examples Specifications i) Reduce by at least – 80 db the influence of d on y in the frequency band ii) Follow with error less than or equal to -40 db the reference signals r in the frequency band iii) Attenuate by at least – 20 db the noise n in the frequency band iv) Static error in response to a unit parabola reference v) Phase Margin vi) Gain Margin

Loop Shaping – Design examples Geometrical constraints; conditions i), iii) i) iii

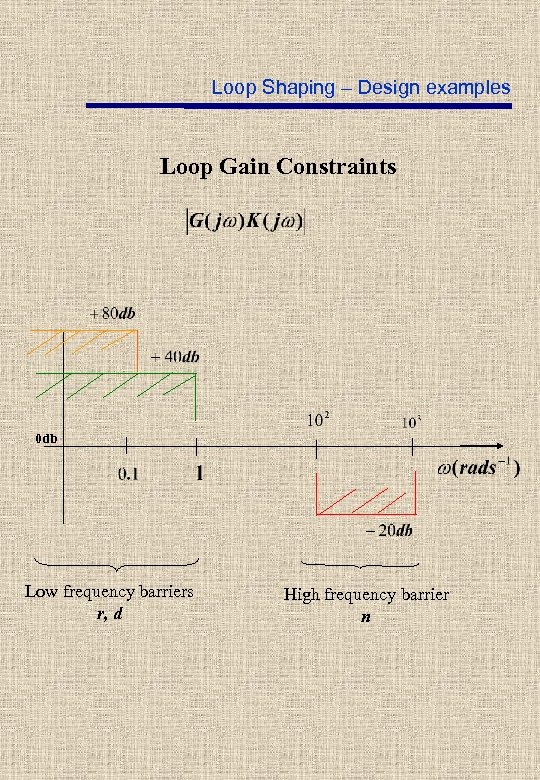
Loop Shaping – Design examples Loop Gain Constraints 0 db Low frequency barriers r, d High frequency barrier n

Loop Shaping – Design examples Condition iv) Static error in response to a unit parabola reference (possible to achieve, because G(s) has two poles at the origin) Let

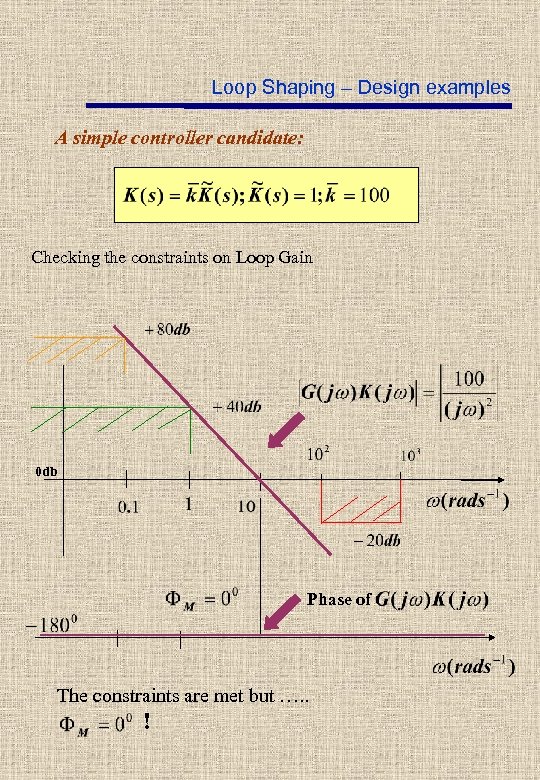
Loop Shaping – Design examples A simple controller candidate: Checking the constraints on Loop Gain 0 db Phase of The constraints are met but …. . !

Loop Shaping – Design examples It is necessary to introduce some phase lead Minimum phase margin (specs): Additional phase required : real phase margin = 0 graus security factor (start by trying security factor = 0). Additional phase required: 450 Pure “PHASE LEAD” network Phase of Phase lead odb z z

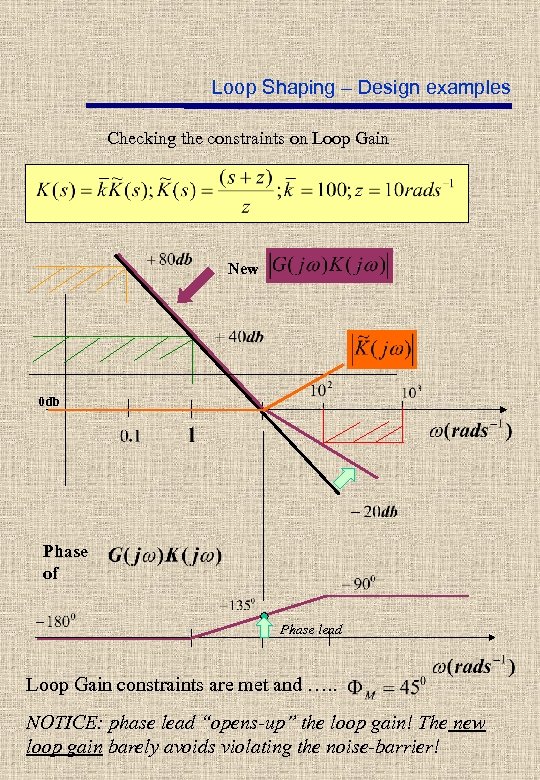
Loop Shaping – Design examples Checking the constraints on Loop Gain New 0 db Phase of Phase lead Loop Gain constraints are met and …. . NOTICE: phase lead “opens-up” the loop gain! The new loop gain barely avoids violating the noise-barrier!

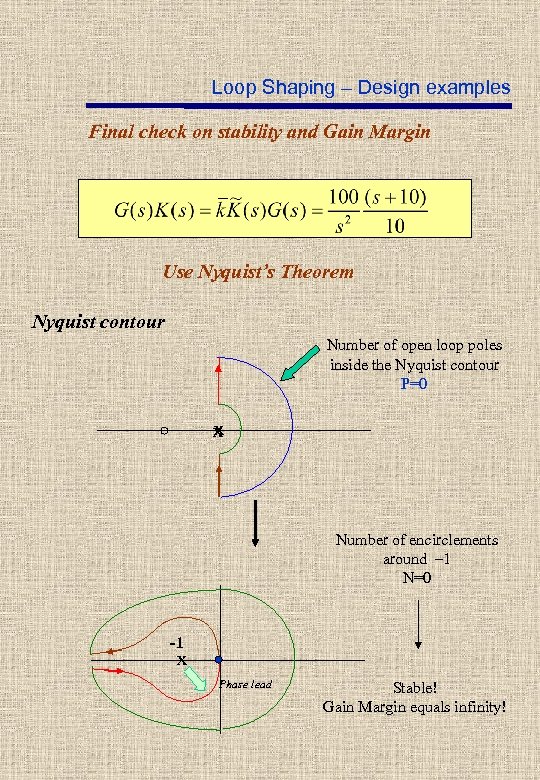
Loop Shaping – Design examples Final check on stability and Gain Margin Use Nyquist’s Theorem Nyquist contour Number of open loop poles inside the Nyquist contour P=0 x Number of encirclements around – 1 N=0 -1 x Phase lead Stable! Gain Margin equals infinity!

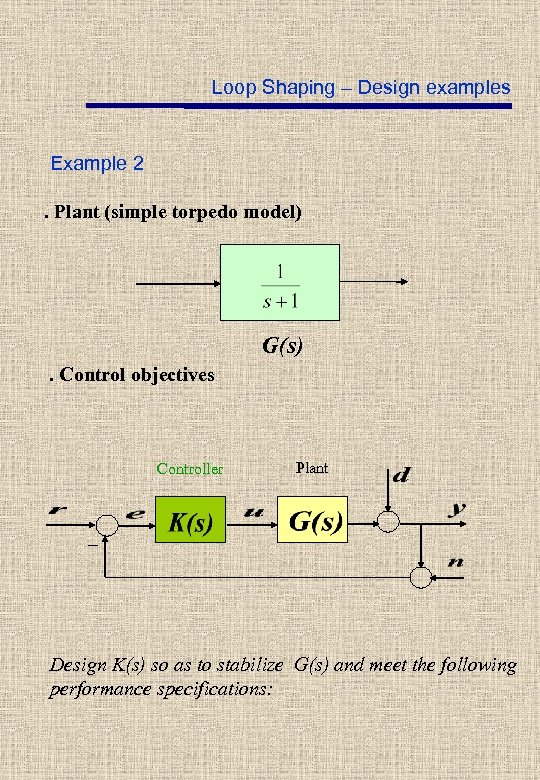
Loop Shaping – Design examples Example 2. Plant (simple torpedo model) G(s). Control objectives Controller Plant _ Design K(s) so as to stabilize G(s) and meet the following performance specifications:

Loop Shaping – Design examples Specifications i) Static position error = 0. ii) Attenuate by at least – 40 db the signals d in the frequency band iii) Follow with error smaller than or equal to -100 db the signals r in the frequency band iv) Attenuate by at least – 40 db the noise n in the frequency band v) Phase Margin vi) Gain Margin

Loop Shaping – Design examples Geometrical constraints; conditions i), iii) iv)

Loop Shaping – Design examples Condition i) Static position error (1 pure integrator in the direct path) A simple controller candidate: Loop Gain

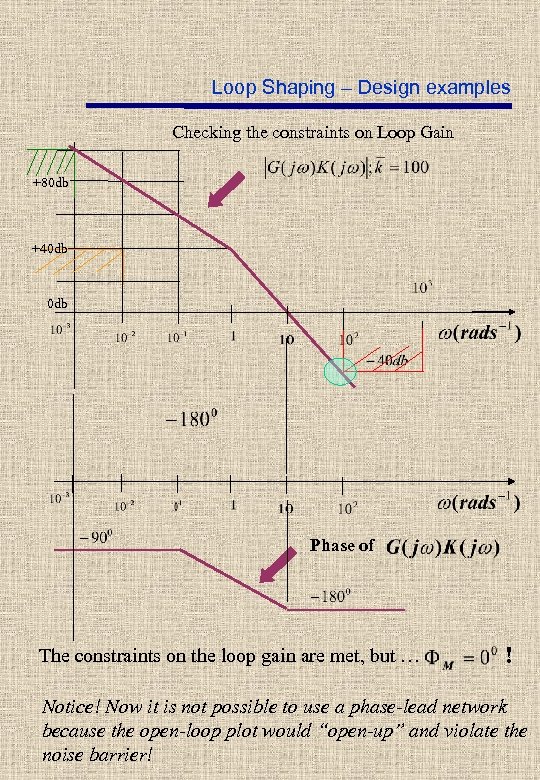
Loop Shaping – Design examples Checking the constraints on Loop Gain +80 db +40 db Phase of The constraints on the loop gain are met, but … ! Notice! Now it is not possible to use a phase-lead network because the open-loop plot would “open-up” and violate the noise barrier!

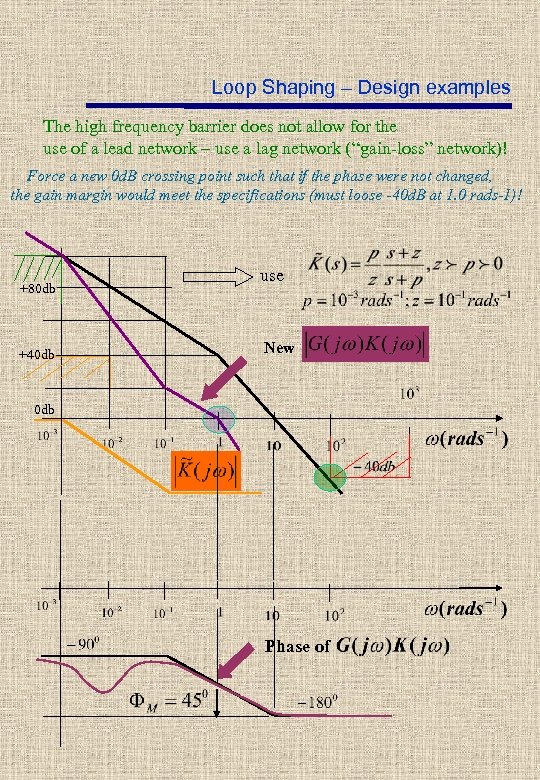
Loop Shaping – Design examples The high frequency barrier does not allow for the use of a lead network – use a lag network (“gain-loss” network)! Force a new 0 d. B crossing point such that if the phase were not changed, the gain margin would meet the specifications (must loose -40 d. B at 1. 0 rads-1)! +80 db +40 db use New 0 db Phase of

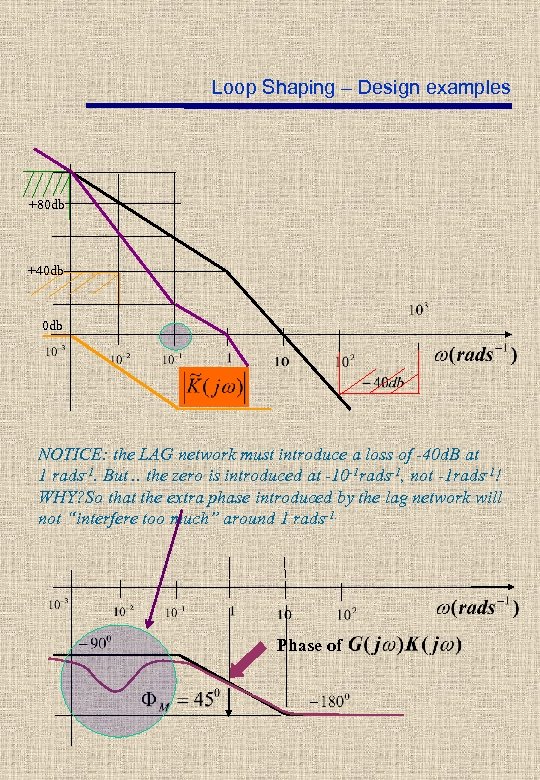
Loop Shaping – Design examples +80 db +40 db NOTICE: the LAG network must introduce a loss of -40 d. B at 1 rads-1. But. . the zero is introduced at -10 -1 rads-1, not -1 rads-1! WHY? So that the extra phase introduced by the lag network will not “interfere too much” around 1 rads-1. Phase of

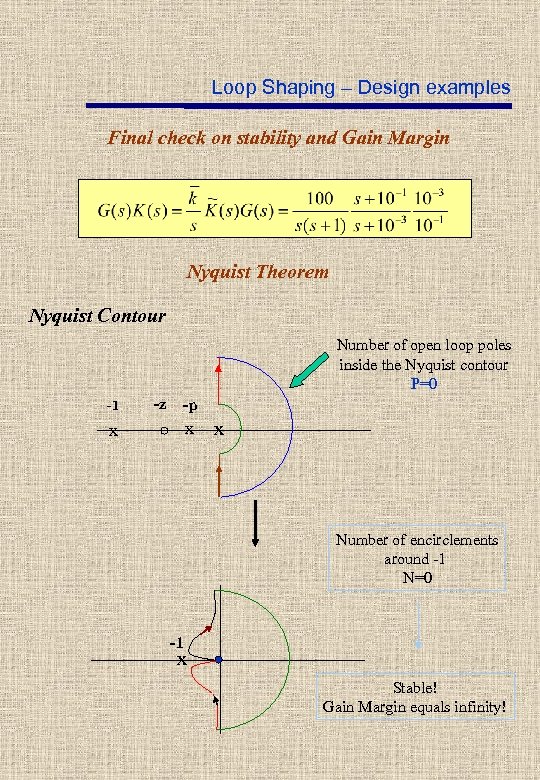
Loop Shaping – Design examples Final check on stability and Gain Margin Nyquist Theorem Nyquist Contour Number of open loop poles inside the Nyquist contour P=0 -1 -z -p x x x Number of encirclements around -1 N=0 -1 x Stable! Gain Margin equals infinity!

Loop Shaping – Design examples Example 3 (Lunar Excursion Module – LEM)

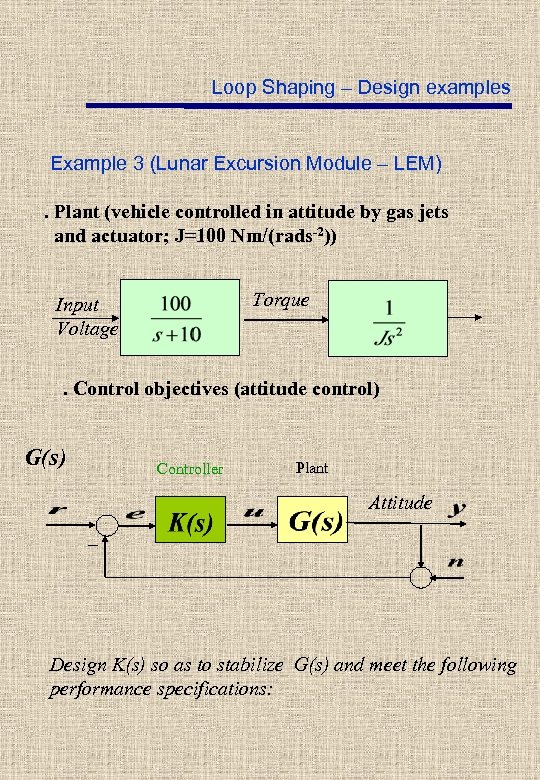
Loop Shaping – Design examples Example 3 (Lunar Excursion Module – LEM). Plant (vehicle controlled in attitude by gas jets and actuator; J=100 Nm/(rads-2)) Torque Input Voltage . Control objectives (attitude control) G(s) Controller Plant Attitude _ Design K(s) so as to stabilize G(s) and meet the following performance specifications:

Loop Shaping – Design examples Specifications i) Static position error = 0. ii) Follow with error smaller than or equal to -40 db the signals r in the frequency band iii) Attenuate by at least – 40 db the noise n in the frequency band iv) Gain Margin v) Phase Margin v) Robustness of stability with respect to a total delay in the control channel of up to 0. 5 sec

Loop Shaping – Design examples Geometrical constraints; conditions ii), iii)

Loop Shaping – Design examples Condition i) Static position error (there already two integrators in the direct path) A simple controller candidate: Loop Gain

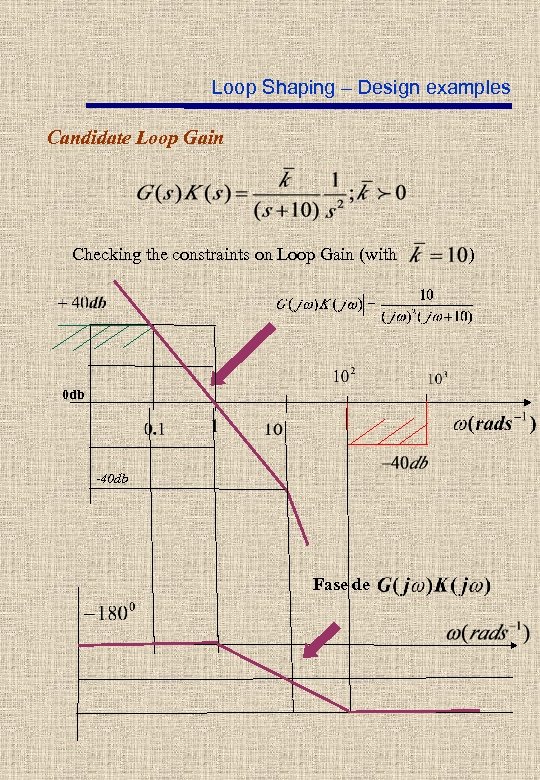
Loop Shaping – Design examples Candidate Loop Gain Checking the constraints on Loop Gain (with 0 db -40 db Fase de )

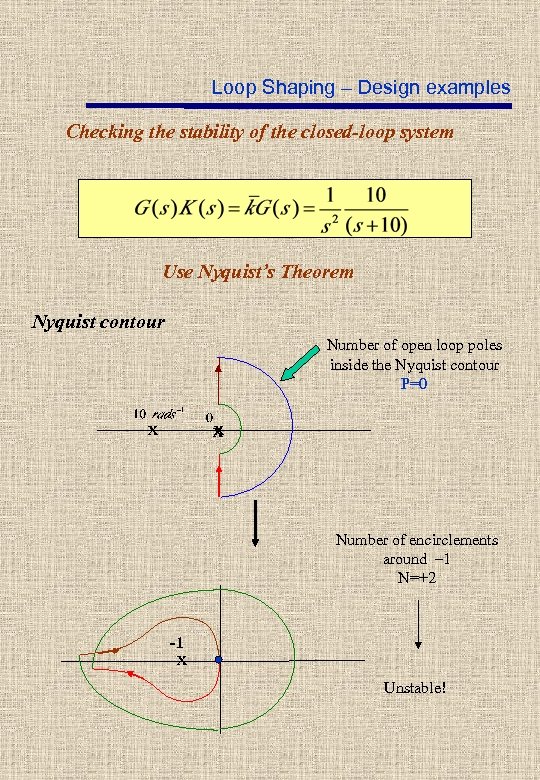
Loop Shaping – Design examples Checking the stability of the closed-loop system Use Nyquist’s Theorem Nyquist contour Number of open loop poles inside the Nyquist contour P=0 x x Number of encirclements around – 1 N=+2 -1 x Unstable!

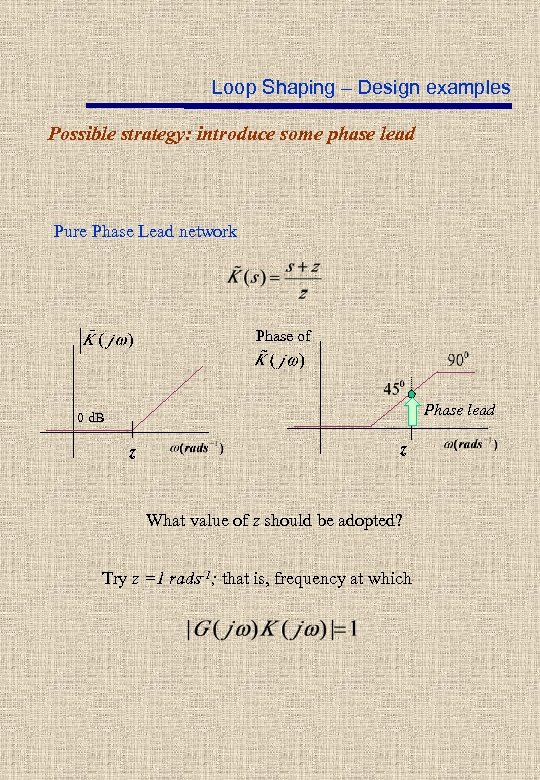
Loop Shaping – Design examples Possible strategy: introduce some phase lead Pure Phase Lead network Phase of Phase lead 0 d. B z z What value of z should be adopted? Try z =1 rads-1; that is, frequency at which

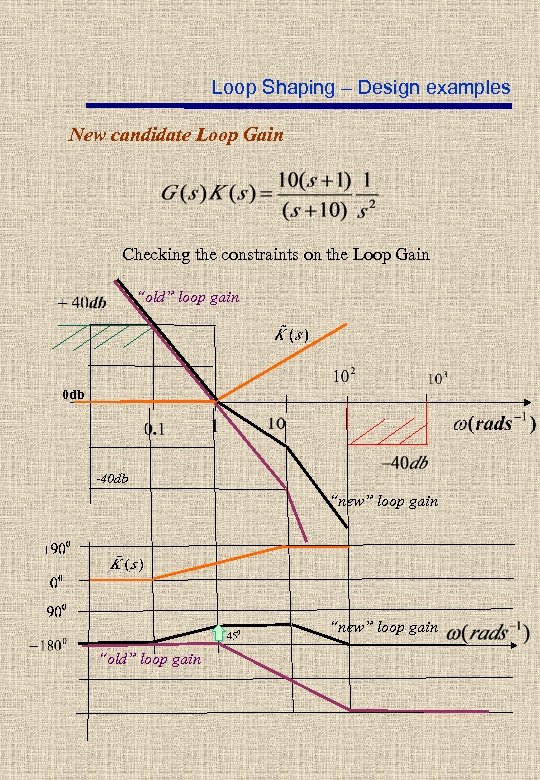
Loop Shaping – Design examples New candidate Loop Gain Checking the constraints on the Loop Gain “old” loop gain 0 db -40 db “new” loop gain “old” loop gain

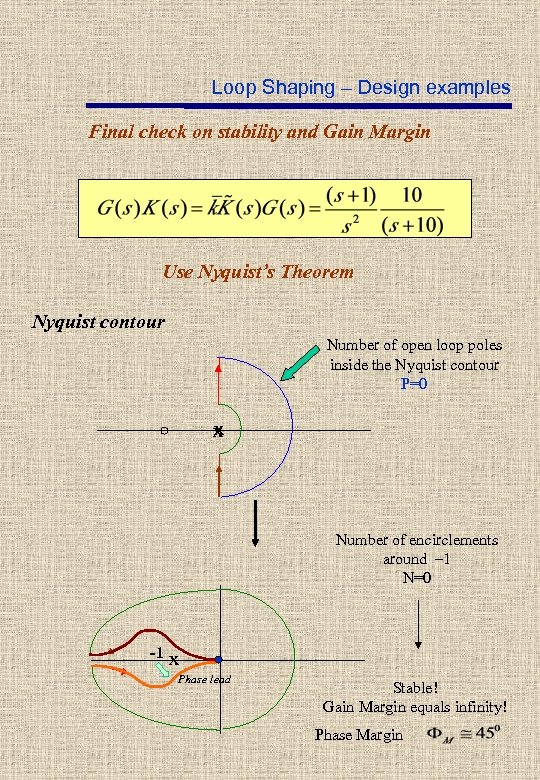
Loop Shaping – Design examples Final check on stability and Gain Margin Use Nyquist’s Theorem Nyquist contour Number of open loop poles inside the Nyquist contour P=0 x Number of encirclements around – 1 N=0 -1 x Phase lead Stable! Gain Margin equals infinity! Phase Margin

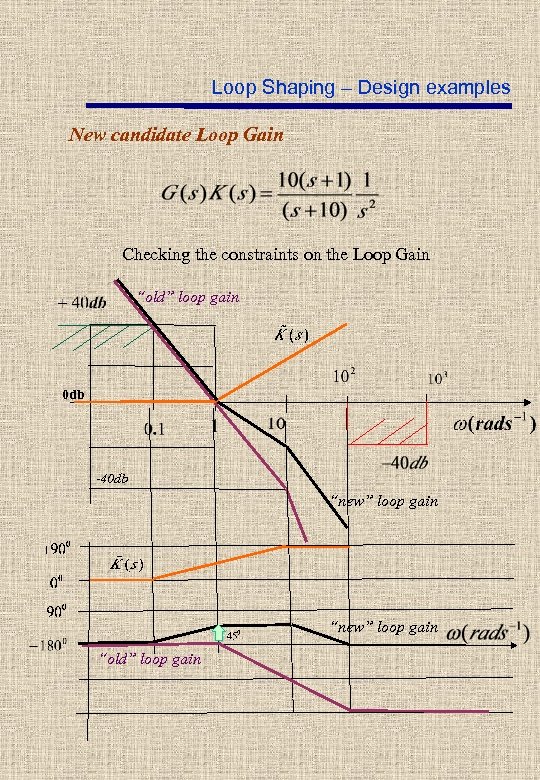
Loop Shaping – Design examples New candidate Loop Gain Checking the constraints on the Loop Gain “old” loop gain 0 db -40 db “new” loop gain “old” loop gain

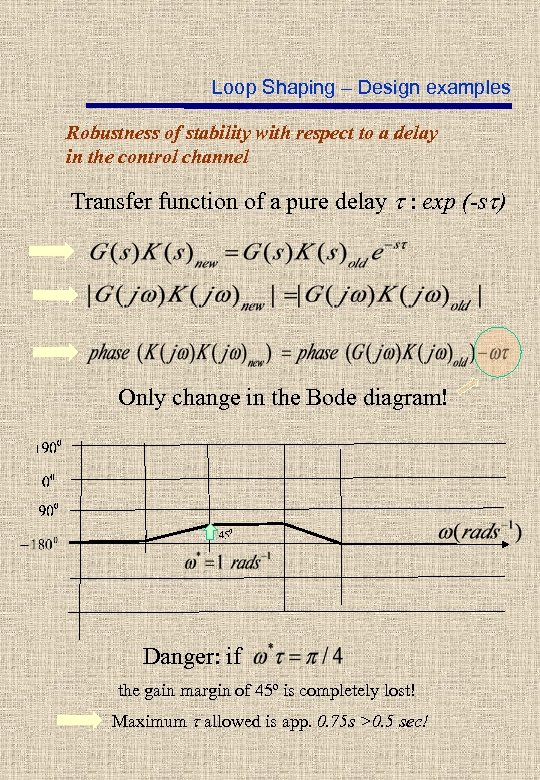
Loop Shaping – Design examples Robustness of stability with respect to a delay in the control channel Transfer function of a pure delay t : exp (-st) Only change in the Bode diagram! Danger: if the gain margin of 45º is completely lost! Maximum t allowed is app. 0. 75 s >0. 5 sec!

Intrinsic Limitations on Achievable Performance Controller Plant _ Simple algebraic limitation Find (if at all possible) a controller K(s) that will stabilize G(s) and such that (reference following spec) (noise attenuation spec) Notice:

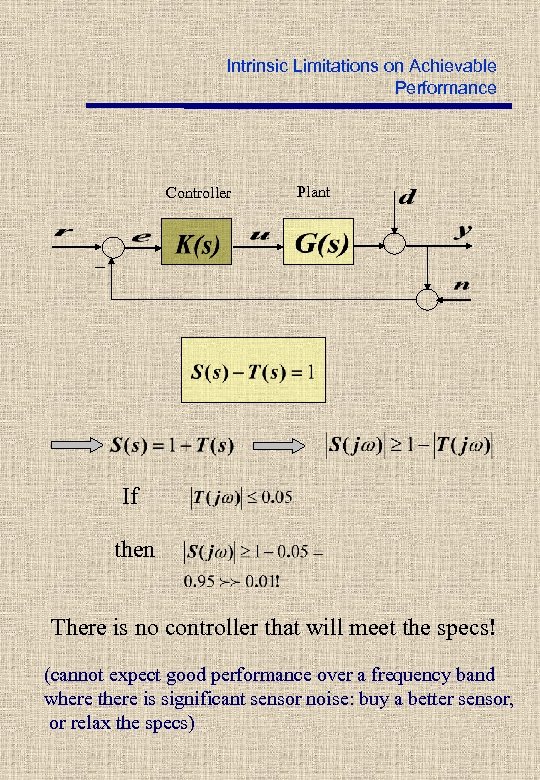
Intrinsic Limitations on Achievable Performance Controller Plant _ If then There is no controller that will meet the specs! (cannot expect good performance over a frequency band where there is significant sensor noise: buy a better sensor, or relax the specs)

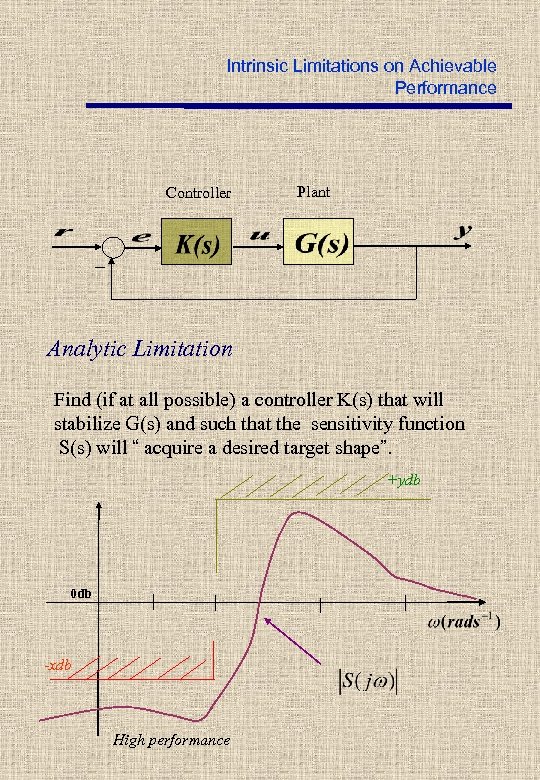
Intrinsic Limitations on Achievable Performance Controller Plant _ Analytic Limitation Find (if at all possible) a controller K(s) that will stabilize G(s) and such that the sensitivity function S(s) will “ acquire a desired target shape”. +ydb 0 db -xdb High performance

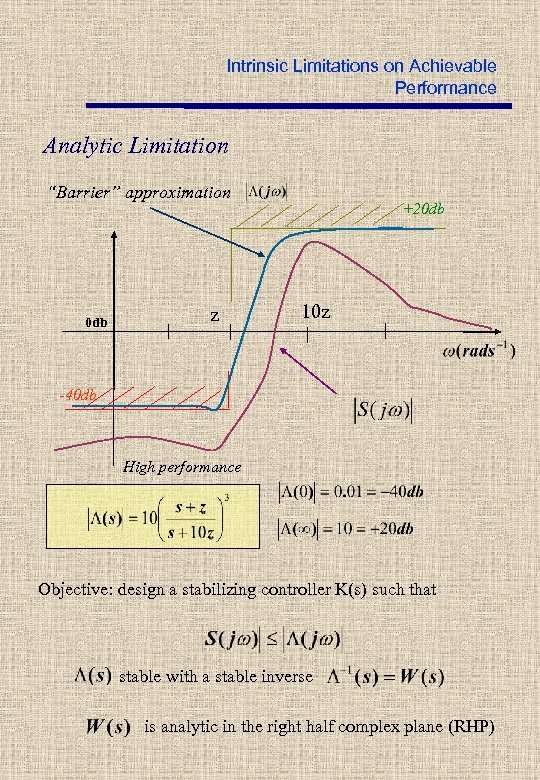
Intrinsic Limitations on Achievable Performance Analytic Limitation “Barrier” approximation 0 db z +20 db 10 z -40 db High performance Objective: design a stabilizing controller K(s) such that stable with a stable inverse is analytic in the right half complex plane (RHP)

Intrinsic Limitations on Achievable Performance If K(s) stabilizes G(s), then S(s) is analytic in the RHP (maximum modulus principle) Suppose the plant G(s) has an “unstable” zero (no unstable pole-zero cancellations) condition to be satisfied!

Intrinsic Limitations on Achievable Performance Case 1. Z=2 rad/s (plant zero “inside” the high performance bandwidth region) Impossible to meet the specifications! Case 1. Z=0. 05 rad/s (plant zero “outside” the high performance bandwidth region) The specs are met.

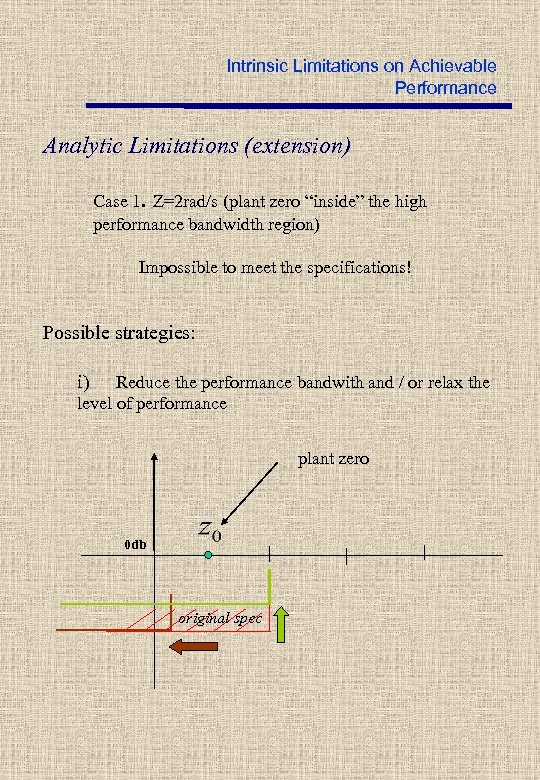
Intrinsic Limitations on Achievable Performance Analytic Limitations (extension) Case 1. Z=2 rad/s (plant zero “inside” the high performance bandwidth region) Impossible to meet the specifications! Possible strategies: i) Reduce the performance bandwith and / or relax the level of performance plant zero 0 db original spec

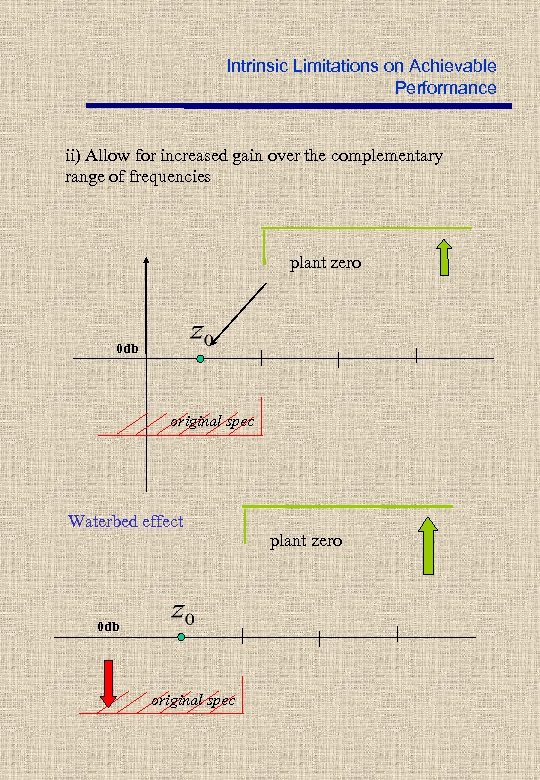
Intrinsic Limitations on Achievable Performance ii) Allow for increased gain over the complementary range of frequencies plant zero 0 db original spec Waterbed effect 0 db original spec plant zero

Intrinsic Limitations on Achievable Performance Open loop (unstable) zeros and poles place fundamental restrictions on what can be done with feedback! (not “textbook” examples) Open loop unstable system Must maintain a given closed loop bandwith (dangerous!) Before designing a controller, take a step back. . examine the system physics. Freudenberg and Looze, “Right half plane poles and zeros and design tradeoffs in feedback systems, ” IEEE Trans. Automatic Control, Vol. 39(6), pp. 55 -565, 1985.

Loop Shaping (SISO case) 0 db António Pascoal 2011 antonio@isr. ist. utl. pt