Тема4Статистические ряды распределения.ppt
- Количество слайдов: 65
 LOGO Статистические ряды распределения
LOGO Статистические ряды распределения
 Статистический ряд распределения – это групповая таблица, имеющая две графы: v группы по выделенному признаку (графа вариант) ; v численность групп (графа частот). www. themegallery. com Company Logo
Статистический ряд распределения – это групповая таблица, имеющая две графы: v группы по выделенному признаку (графа вариант) ; v численность групп (графа частот). www. themegallery. com Company Logo
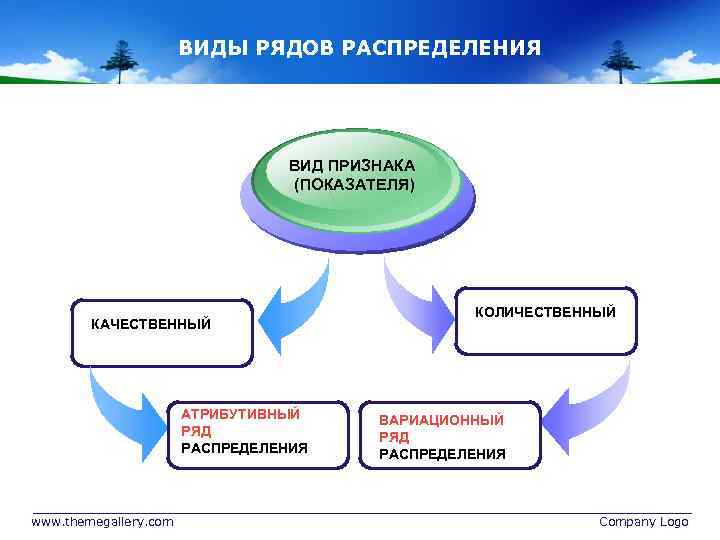 ВИДЫ РЯДОВ РАСПРЕДЕЛЕНИЯ ВИД ПРИЗНАКА (ПОКАЗАТЕЛЯ) КАЧЕСТВЕННЫЙ АТРИБУТИВНЫЙ РЯД РАСПРЕДЕЛЕНИЯ www. themegallery. com КОЛИЧЕСТВЕННЫЙ ВАРИАЦИОННЫЙ РЯД РАСПРЕДЕЛЕНИЯ Company Logo
ВИДЫ РЯДОВ РАСПРЕДЕЛЕНИЯ ВИД ПРИЗНАКА (ПОКАЗАТЕЛЯ) КАЧЕСТВЕННЫЙ АТРИБУТИВНЫЙ РЯД РАСПРЕДЕЛЕНИЯ www. themegallery. com КОЛИЧЕСТВЕННЫЙ ВАРИАЦИОННЫЙ РЯД РАСПРЕДЕЛЕНИЯ Company Logo
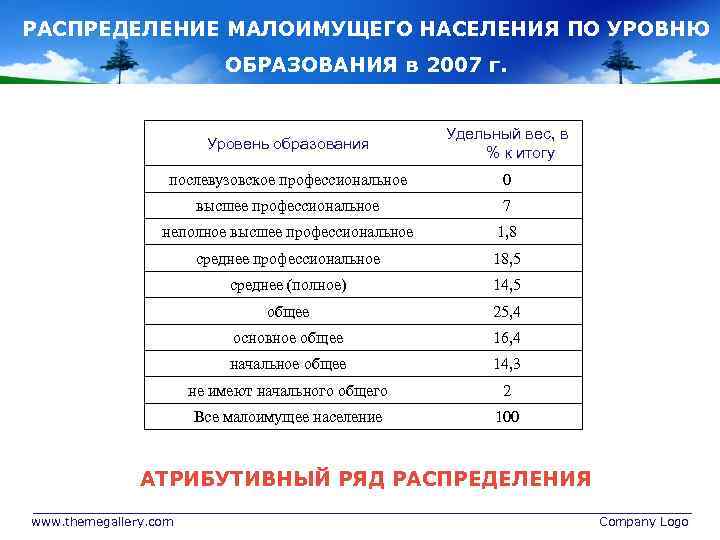 РАСПРЕДЕЛЕНИЕ МАЛОИМУЩЕГО НАСЕЛЕНИЯ ПО УРОВНЮ ОБРАЗОВАНИЯ в 2007 г. Уровень образования Удельный вес, в % к итогу послевузовское профессиональное 0 высшее профессиональное 7 неполное высшее профессиональное 1, 8 среднее профессиональное 18, 5 среднее (полное) 14, 5 общее 25, 4 основное общее 16, 4 начальное общее 14, 3 не имеют начального общего 2 Все малоимущее население 100 АТРИБУТИВНЫЙ РЯД РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
РАСПРЕДЕЛЕНИЕ МАЛОИМУЩЕГО НАСЕЛЕНИЯ ПО УРОВНЮ ОБРАЗОВАНИЯ в 2007 г. Уровень образования Удельный вес, в % к итогу послевузовское профессиональное 0 высшее профессиональное 7 неполное высшее профессиональное 1, 8 среднее профессиональное 18, 5 среднее (полное) 14, 5 общее 25, 4 основное общее 16, 4 начальное общее 14, 3 не имеют начального общего 2 Все малоимущее население 100 АТРИБУТИВНЫЙ РЯД РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
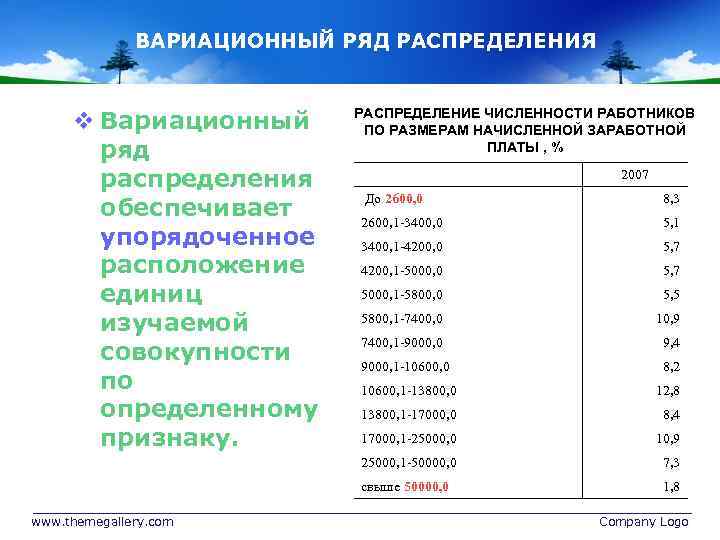 ВАРИАЦИОННЫЙ РЯД РАСПРЕДЕЛЕНИЯ v Вариационный ряд распределения обеспечивает упорядоченное расположение единиц изучаемой совокупности по определенному признаку. РАСПРЕДЕЛЕНИЕ ЧИСЛЕННОСТИ РАБОТНИКОВ ПО РАЗМЕРАМ НАЧИСЛЕННОЙ ЗАРАБОТНОЙ ПЛАТЫ , % 2007 8, 3 2600, 1 -3400, 0 5, 1 3400, 1 -4200, 0 5, 7 4200, 1 -5000, 0 5, 7 5000, 1 -5800, 0 5, 5 5800, 1 -7400, 0 10, 9 7400, 1 -9000, 0 9, 4 9000, 1 -10600, 0 8, 2 10600, 1 -13800, 0 12, 8 13800, 1 -17000, 0 8, 4 17000, 1 -25000, 0 10, 9 25000, 1 -50000, 0 7, 3 свыше 50000, 0 www. themegallery. com До 2600, 0 1, 8 Company Logo
ВАРИАЦИОННЫЙ РЯД РАСПРЕДЕЛЕНИЯ v Вариационный ряд распределения обеспечивает упорядоченное расположение единиц изучаемой совокупности по определенному признаку. РАСПРЕДЕЛЕНИЕ ЧИСЛЕННОСТИ РАБОТНИКОВ ПО РАЗМЕРАМ НАЧИСЛЕННОЙ ЗАРАБОТНОЙ ПЛАТЫ , % 2007 8, 3 2600, 1 -3400, 0 5, 1 3400, 1 -4200, 0 5, 7 4200, 1 -5000, 0 5, 7 5000, 1 -5800, 0 5, 5 5800, 1 -7400, 0 10, 9 7400, 1 -9000, 0 9, 4 9000, 1 -10600, 0 8, 2 10600, 1 -13800, 0 12, 8 13800, 1 -17000, 0 8, 4 17000, 1 -25000, 0 10, 9 25000, 1 -50000, 0 7, 3 свыше 50000, 0 www. themegallery. com До 2600, 0 1, 8 Company Logo
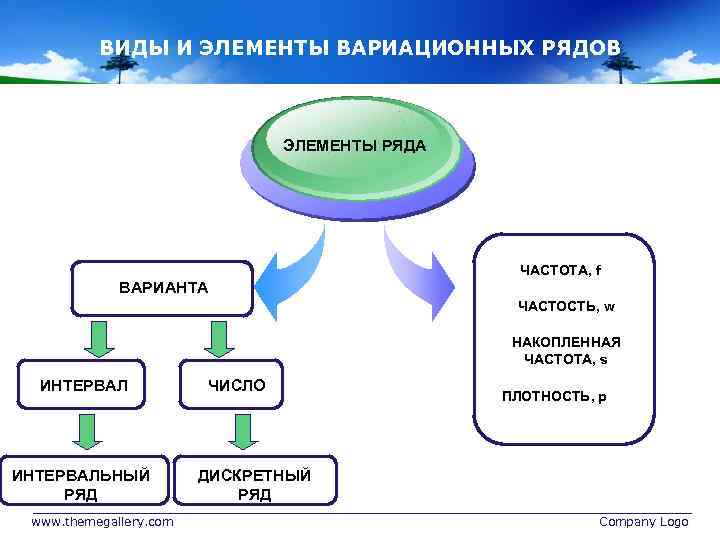 ВИДЫ И ЭЛЕМЕНТЫ ВАРИАЦИОННЫХ РЯДОВ ЭЛЕМЕНТЫ РЯДА ЧАСТОТА, f ВАРИАНТА ЧАСТОСТЬ, w НАКОПЛЕННАЯ ЧАСТОТА, s ИНТЕРВАЛЬНЫЙ РЯД www. themegallery. com ЧИСЛО ПЛОТНОСТЬ, р ДИСКРЕТНЫЙ РЯД Company Logo
ВИДЫ И ЭЛЕМЕНТЫ ВАРИАЦИОННЫХ РЯДОВ ЭЛЕМЕНТЫ РЯДА ЧАСТОТА, f ВАРИАНТА ЧАСТОСТЬ, w НАКОПЛЕННАЯ ЧАСТОТА, s ИНТЕРВАЛЬНЫЙ РЯД www. themegallery. com ЧИСЛО ПЛОТНОСТЬ, р ДИСКРЕТНЫЙ РЯД Company Logo
 Варианта - это отдельное значение или интервал изменения признака, которое он принимает в ряду распределения, обозначается буквой хi или х’i. Частота - это численность вариант в i-ой группе (интервале) вариационного ряда, обозначается fi. Сумма частот называется объем совокупности (N или n). www. themegallery. com Company Logo
Варианта - это отдельное значение или интервал изменения признака, которое он принимает в ряду распределения, обозначается буквой хi или х’i. Частота - это численность вариант в i-ой группе (интервале) вариационного ряда, обозначается fi. Сумма частот называется объем совокупности (N или n). www. themegallery. com Company Logo
 ЧАСТОСТЬ или ОТНОСИТЕЛЬНАЯ ЧАСТОТА Частоты, выраженные в долях единицы, называются частостями Частости позволяют сравнивать ряды с различным числом наблюдений, они являются оценкой вероятности появления хi в совокупности наблюдений www. themegallery. com Company Logo
ЧАСТОСТЬ или ОТНОСИТЕЛЬНАЯ ЧАСТОТА Частоты, выраженные в долях единицы, называются частостями Частости позволяют сравнивать ряды с различным числом наблюдений, они являются оценкой вероятности появления хi в совокупности наблюдений www. themegallery. com Company Logo
 НАКОПЛЕННАЯ ЧАСТОТА Накопленная частота (Si) – число единиц совокупности, имеющих значение признака меньше или равных Xi www. themegallery. com Company Logo
НАКОПЛЕННАЯ ЧАСТОТА Накопленная частота (Si) – число единиц совокупности, имеющих значение признака меньше или равных Xi www. themegallery. com Company Logo
 ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ Абсолютная плотность распределения (p) – величина частоты, приходящаяся на единицу величины интервала: Pi=fi/hi Относительная плотность распределения : р’ = Wi/hi Показатели используются вместо частоты и частости, когда в интервальном ряду распределения интервалы неравные www. themegallery. com Company Logo
ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ Абсолютная плотность распределения (p) – величина частоты, приходящаяся на единицу величины интервала: Pi=fi/hi Относительная плотность распределения : р’ = Wi/hi Показатели используются вместо частоты и частости, когда в интервальном ряду распределения интервалы неравные www. themegallery. com Company Logo
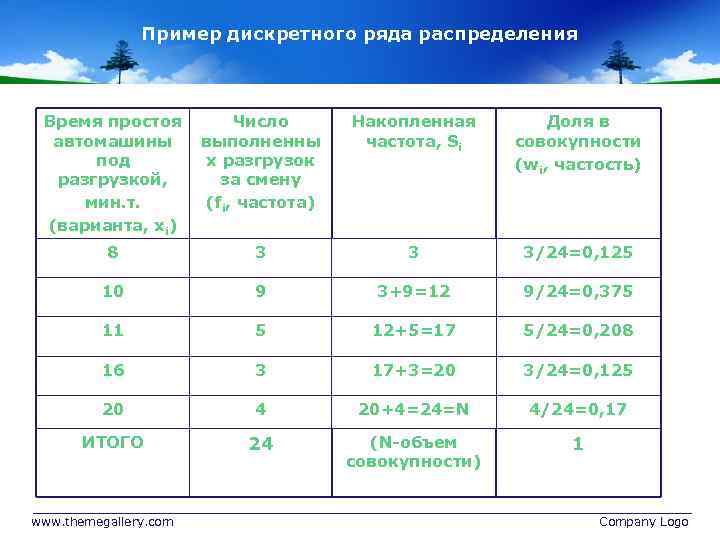 Пример дискретного ряда распределения Время простоя автомашины под разгрузкой, мин. т. (варианта, хi) Число выполненны х разгрузок за смену (fi, частота) Накопленная частота, Si Доля в совокупности (wi, частость) 8 3 3 3/24=0, 125 10 9 3+9=12 9/24=0, 375 11 5 12+5=17 5/24=0, 208 16 3 17+3=20 3/24=0, 125 20 4 20+4=24=N 4/24=0, 17 ИТОГО 24 (N-объем совокупности) 1 www. themegallery. com Company Logo
Пример дискретного ряда распределения Время простоя автомашины под разгрузкой, мин. т. (варианта, хi) Число выполненны х разгрузок за смену (fi, частота) Накопленная частота, Si Доля в совокупности (wi, частость) 8 3 3 3/24=0, 125 10 9 3+9=12 9/24=0, 375 11 5 12+5=17 5/24=0, 208 16 3 17+3=20 3/24=0, 125 20 4 20+4=24=N 4/24=0, 17 ИТОГО 24 (N-объем совокупности) 1 www. themegallery. com Company Logo
 Пример интервального ряда распределения Основные фонды, млн. руб. (варианта, хi) Число организаций (fi, частота) Плотность (рi=fi/hi) Относительная плотность Pi’=wi/hi 1, 0 – 2, 0 3 3/1=3 0, 18/1=0, 18 2, 0 – 5, 0 9 9/3=3 0, 53/3=0, 18 5, 0 -10, 0 5 5/5=1 0, 29/5=0, 06 ИТОГО 17 www. themegallery. com Company Logo
Пример интервального ряда распределения Основные фонды, млн. руб. (варианта, хi) Число организаций (fi, частота) Плотность (рi=fi/hi) Относительная плотность Pi’=wi/hi 1, 0 – 2, 0 3 3/1=3 0, 18/1=0, 18 2, 0 – 5, 0 9 9/3=3 0, 53/3=0, 18 5, 0 -10, 0 5 5/5=1 0, 29/5=0, 06 ИТОГО 17 www. themegallery. com Company Logo
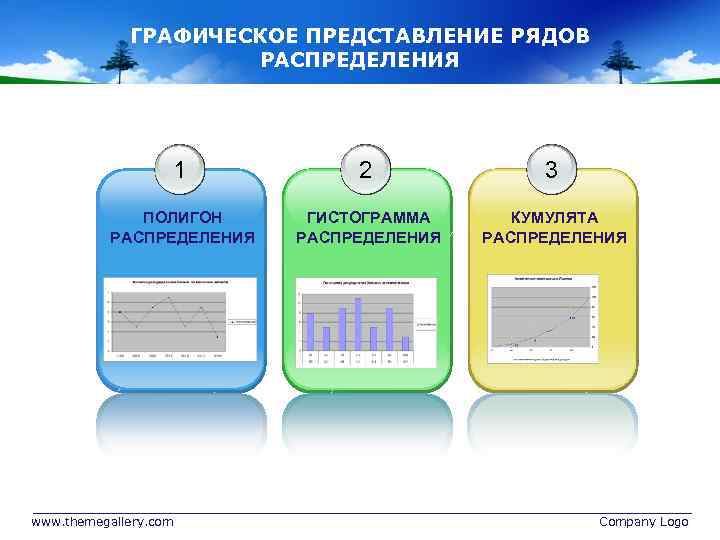 ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЯДОВ РАСПРЕДЕЛЕНИЯ 1 2 3 ПОЛИГОН РАСПРЕДЕЛЕНИЯ ГИСТОГРАММА РАСПРЕДЕЛЕНИЯ КУМУЛЯТА РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЯДОВ РАСПРЕДЕЛЕНИЯ 1 2 3 ПОЛИГОН РАСПРЕДЕЛЕНИЯ ГИСТОГРАММА РАСПРЕДЕЛЕНИЯ КУМУЛЯТА РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
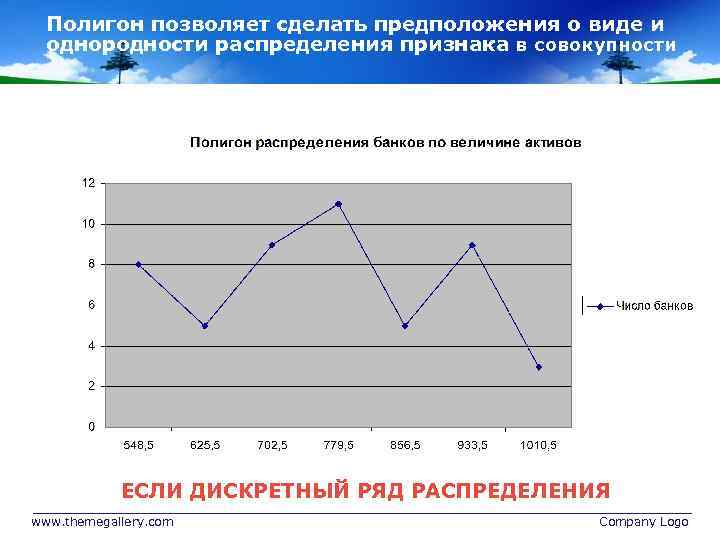 Полигон позволяет сделать предположения о виде и однородности распределения признака в совокупности ЕСЛИ ДИСКРЕТНЫЙ РЯД РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
Полигон позволяет сделать предположения о виде и однородности распределения признака в совокупности ЕСЛИ ДИСКРЕТНЫЙ РЯД РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
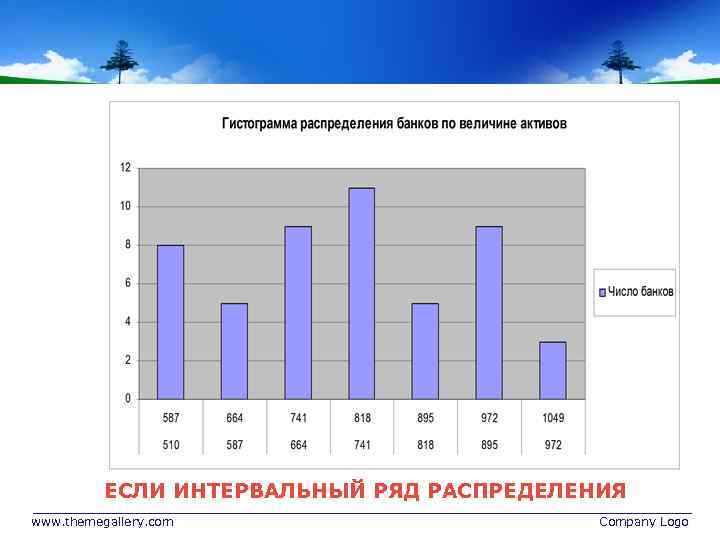 ЕСЛИ ИНТЕРВАЛЬНЫЙ РЯД РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
ЕСЛИ ИНТЕРВАЛЬНЫЙ РЯД РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
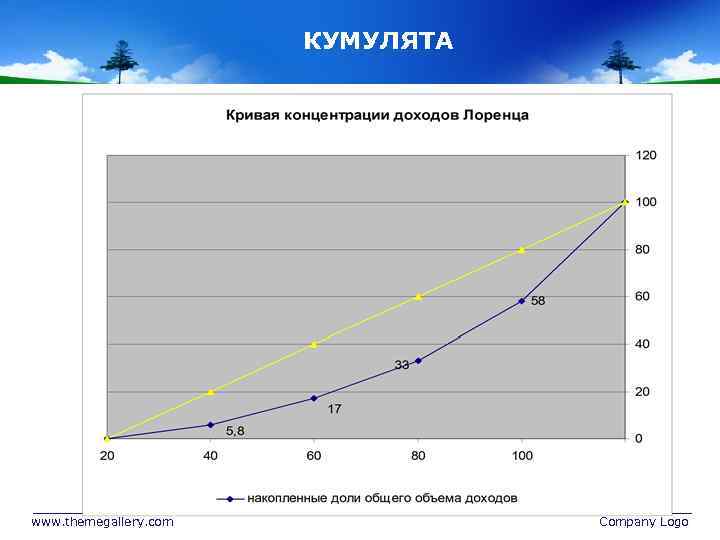 КУМУЛЯТА www. themegallery. com Company Logo
КУМУЛЯТА www. themegallery. com Company Logo
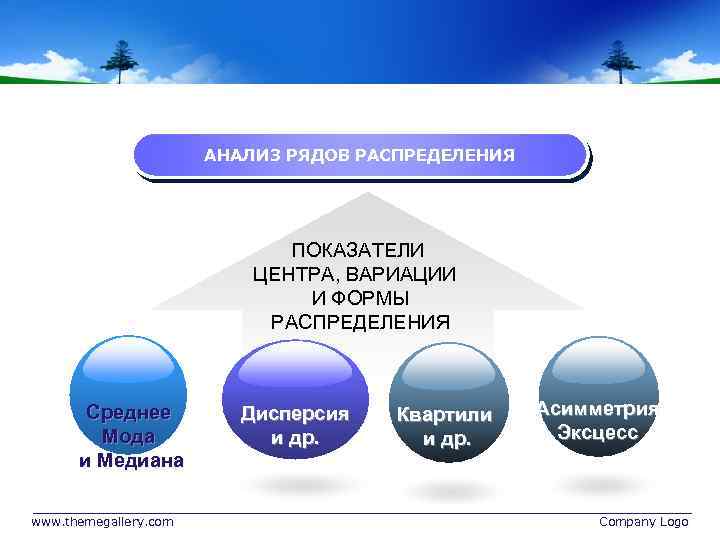 АНАЛИЗ РЯДОВ РАСПРЕДЕЛЕНИЯ ПОКАЗАТЕЛИ ЦЕНТРА, ВАРИАЦИИ И ФОРМЫ РАСПРЕДЕЛЕНИЯ Среднее Мода и Медиана www. themegallery. com Дисперсия и др. Квартили и др. Асимметрия Эксцесс Company Logo
АНАЛИЗ РЯДОВ РАСПРЕДЕЛЕНИЯ ПОКАЗАТЕЛИ ЦЕНТРА, ВАРИАЦИИ И ФОРМЫ РАСПРЕДЕЛЕНИЯ Среднее Мода и Медиана www. themegallery. com Дисперсия и др. Квартили и др. Асимметрия Эксцесс Company Logo
 ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ www. themegallery. com Company Logo
 Среднее значение в дискретном ряду распределения www. themegallery. com Company Logo
Среднее значение в дискретном ряду распределения www. themegallery. com Company Logo
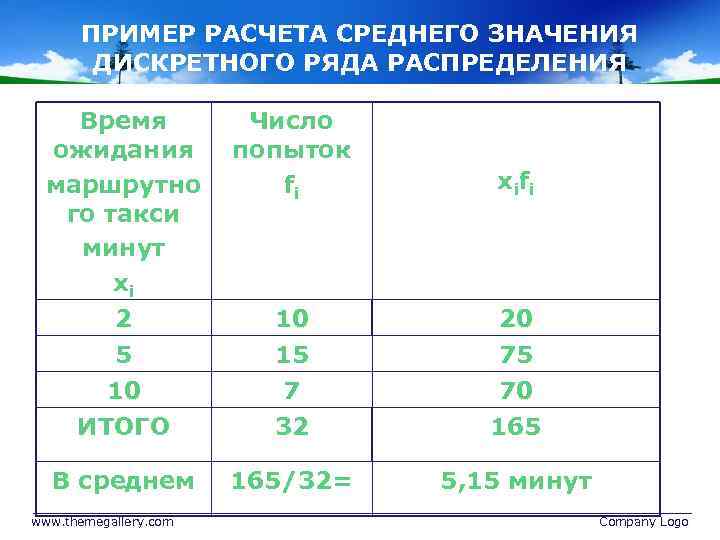 ПРИМЕР РАСЧЕТА СРЕДНЕГО ЗНАЧЕНИЯ ДИСКРЕТНОГО РЯДА РАСПРЕДЕЛЕНИЯ Время ожидания маршрутно го такси минут хi 2 5 10 ИТОГО Число попыток fi х i fi 10 15 7 32 20 75 70 165 В среднем 165/32= 5, 15 минут www. themegallery. com Company Logo
ПРИМЕР РАСЧЕТА СРЕДНЕГО ЗНАЧЕНИЯ ДИСКРЕТНОГО РЯДА РАСПРЕДЕЛЕНИЯ Время ожидания маршрутно го такси минут хi 2 5 10 ИТОГО Число попыток fi х i fi 10 15 7 32 20 75 70 165 В среднем 165/32= 5, 15 минут www. themegallery. com Company Logo
 Среднее значение в интервальном ряду распределения www. themegallery. com Company Logo
Среднее значение в интервальном ряду распределения www. themegallery. com Company Logo
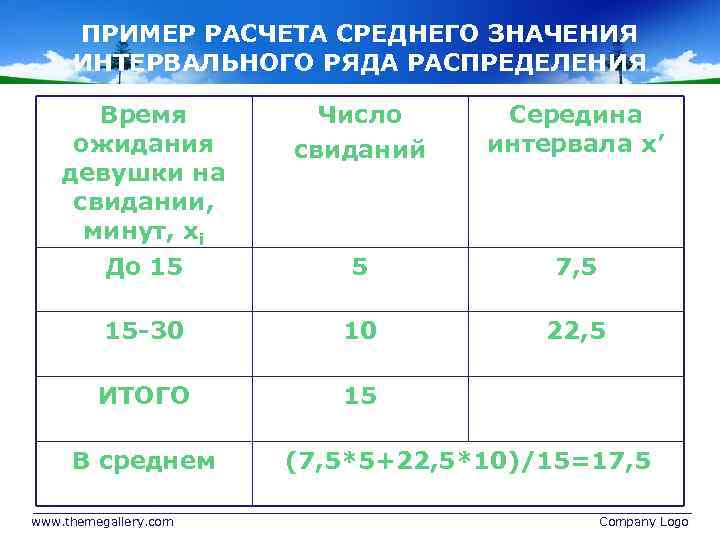 ПРИМЕР РАСЧЕТА СРЕДНЕГО ЗНАЧЕНИЯ ИНТЕРВАЛЬНОГО РЯДА РАСПРЕДЕЛЕНИЯ Время ожидания девушки на свидании, минут, хi Число свиданий Середина интервала х’ До 15 5 7, 5 15 -30 10 22, 5 ИТОГО 15 В среднем www. themegallery. com (7, 5*5+22, 5*10)/15=17, 5 Company Logo
ПРИМЕР РАСЧЕТА СРЕДНЕГО ЗНАЧЕНИЯ ИНТЕРВАЛЬНОГО РЯДА РАСПРЕДЕЛЕНИЯ Время ожидания девушки на свидании, минут, хi Число свиданий Середина интервала х’ До 15 5 7, 5 15 -30 10 22, 5 ИТОГО 15 В среднем www. themegallery. com (7, 5*5+22, 5*10)/15=17, 5 Company Logo
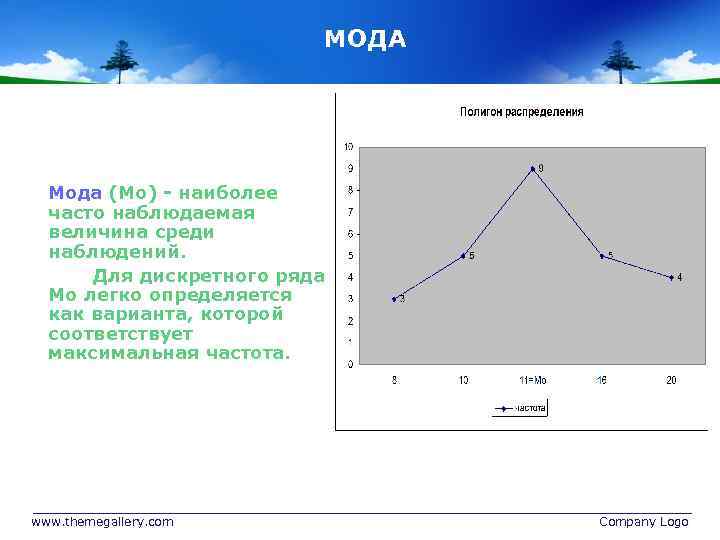 МОДА Мода (Мо) - наиболее часто наблюдаемая величина среди наблюдений. Для дискретного ряда Мо легко определяется как варианта, которой соответствует максимальная частота. www. themegallery. com Company Logo
МОДА Мода (Мо) - наиболее часто наблюдаемая величина среди наблюдений. Для дискретного ряда Мо легко определяется как варианта, которой соответствует максимальная частота. www. themegallery. com Company Logo
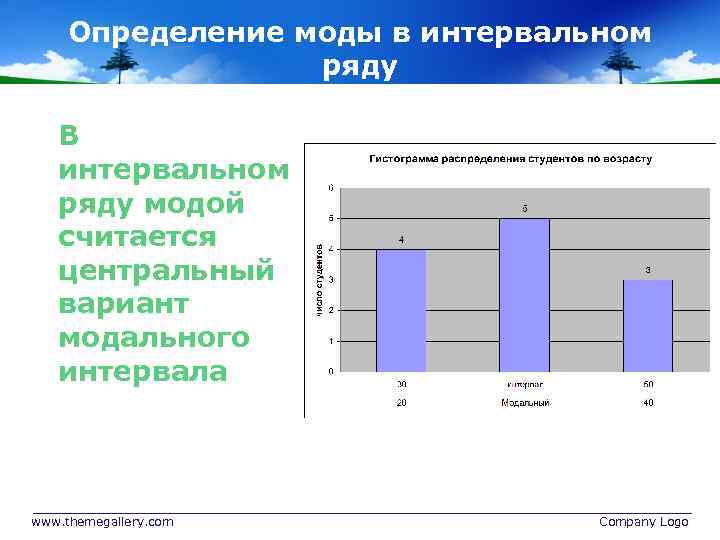 Определение моды в интервальном ряду В интервальном ряду модой считается центральный вариант модального интервала www. themegallery. com Company Logo
Определение моды в интервальном ряду В интервальном ряду модой считается центральный вариант модального интервала www. themegallery. com Company Logo
 Формула оценки Мо для интервального ряда где х0 - нижняя граница модального интервала; h - величина модального интервала; ƒМо - частота модального интервала; ƒМо+1 - частота интервала следующего за модальным интервалом. ƒМо-1 - частота интервала предшествующего модальному интервалу. www. themegallery. com Company Logo
Формула оценки Мо для интервального ряда где х0 - нижняя граница модального интервала; h - величина модального интервала; ƒМо - частота модального интервала; ƒМо+1 - частота интервала следующего за модальным интервалом. ƒМо-1 - частота интервала предшествующего модальному интервалу. www. themegallery. com Company Logo
 МЕДИАНА Me - это величина, которая делит численность упорядоченного вариационного ряда на две равные части 50%: 50% www. themegallery. com Company Logo
МЕДИАНА Me - это величина, которая делит численность упорядоченного вариационного ряда на две равные части 50%: 50% www. themegallery. com Company Logo
 МЕДИАНА для ранжированного ряда с нечетным числом членов Ме - варианта, расположенная в центре ряда Например, прогнозируемый экспертами период окончания строительства электростанции: 2 года 2 года 3 года 5 лет В качестве экспертной оценки всегда выбирается медианное значение, то есть 3 года. www. themegallery. com Company Logo
МЕДИАНА для ранжированного ряда с нечетным числом членов Ме - варианта, расположенная в центре ряда Например, прогнозируемый экспертами период окончания строительства электростанции: 2 года 2 года 3 года 5 лет В качестве экспертной оценки всегда выбирается медианное значение, то есть 3 года. www. themegallery. com Company Logo
 МЕДИАНА для ранжированного ряда с четным числом членов Ме является средняя арифметическая из двух смежных вариант, стоящих на середине ряда. Например, прогнозируемый экспертами период окончания строительства электростанции: 2 года 2 года 3 года 5 лет Экспертная оценка (Ме) = (2+3)/2=2, 5 года www. themegallery. com Company Logo
МЕДИАНА для ранжированного ряда с четным числом членов Ме является средняя арифметическая из двух смежных вариант, стоящих на середине ряда. Например, прогнозируемый экспертами период окончания строительства электростанции: 2 года 2 года 3 года 5 лет Экспертная оценка (Ме) = (2+3)/2=2, 5 года www. themegallery. com Company Logo
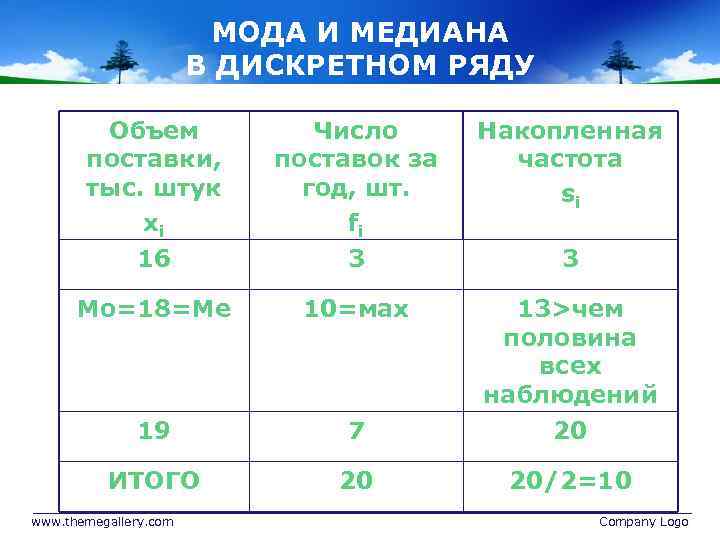 МОДА И МЕДИАНА В ДИСКРЕТНОМ РЯДУ Объем поставки, тыс. штук хi Число поставок за год, шт. fi Накопленная частота si 16 3 3 Мо=18=Ме 10=мах 19 7 13>чем половина всех наблюдений 20 ИТОГО 20 20/2=10 www. themegallery. com Company Logo
МОДА И МЕДИАНА В ДИСКРЕТНОМ РЯДУ Объем поставки, тыс. штук хi Число поставок за год, шт. fi Накопленная частота si 16 3 3 Мо=18=Ме 10=мах 19 7 13>чем половина всех наблюдений 20 ИТОГО 20 20/2=10 www. themegallery. com Company Logo
 Формула для оценки медианы в равно интервальном ряду где х0 - нижняя граница медианного интервала; h- величина медианного интервала; ∑ƒ -сумма частот ряда; SМе-1 - сумма частот в интервалах, предшествующих медианному; ƒМе - частота медианного интервала. www. themegallery. com Company Logo
Формула для оценки медианы в равно интервальном ряду где х0 - нижняя граница медианного интервала; h- величина медианного интервала; ∑ƒ -сумма частот ряда; SМе-1 - сумма частот в интервалах, предшествующих медианному; ƒМе - частота медианного интервала. www. themegallery. com Company Logo
 Мо и Ме в интервальном ряду Объем продаж, млн. руб. , хi До 18 Число человек fi 5 Si 5 18 -20 Модальный и медианный интервалы ИТОГО 10=max 15>7, 5 Мо=18+2((10 -5)/((105)+(10 -0)))=18, 7 Ме=18+2((7, 55)/10)=18, 5 www. themegallery. com 15 - Company Logo
Мо и Ме в интервальном ряду Объем продаж, млн. руб. , хi До 18 Число человек fi 5 Si 5 18 -20 Модальный и медианный интервалы ИТОГО 10=max 15>7, 5 Мо=18+2((10 -5)/((105)+(10 -0)))=18, 7 Ме=18+2((7, 55)/10)=18, 5 www. themegallery. com 15 - Company Logo
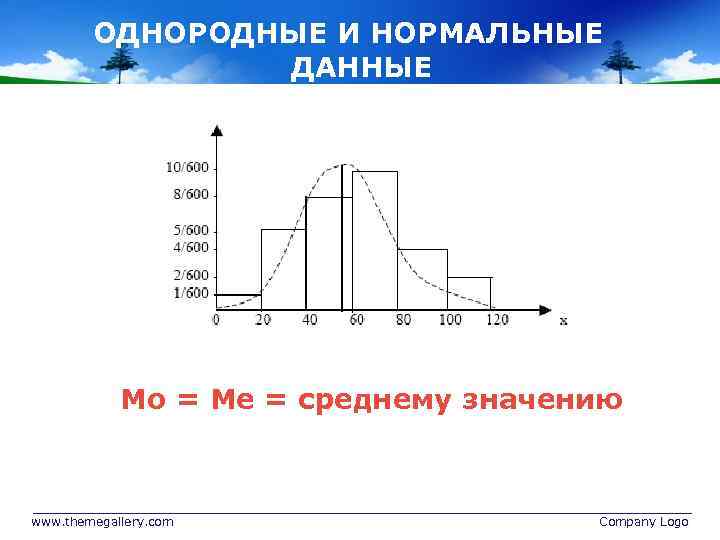 ОДНОРОДНЫЕ И НОРМАЛЬНЫЕ ДАННЫЕ Мо = Ме = среднему значению www. themegallery. com Company Logo
ОДНОРОДНЫЕ И НОРМАЛЬНЫЕ ДАННЫЕ Мо = Ме = среднему значению www. themegallery. com Company Logo
 ПОКАЗАТЕЛИ ВАРИАЦИИ РАСПРЕДЕЛЕНИЯ ПРИЗНАКА www. themegallery. com Company Logo
ПОКАЗАТЕЛИ ВАРИАЦИИ РАСПРЕДЕЛЕНИЯ ПРИЗНАКА www. themegallery. com Company Logo
 ВАРИАЦИЯ Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. www. themegallery. com Company Logo
ВАРИАЦИЯ Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. www. themegallery. com Company Logo
 ОТКУДА БЕРЕТСЯ? Вариация возникает в результате того, что индивидуальные значения признака формируются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. www. themegallery. com Company Logo
ОТКУДА БЕРЕТСЯ? Вариация возникает в результате того, что индивидуальные значения признака формируются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. www. themegallery. com Company Logo
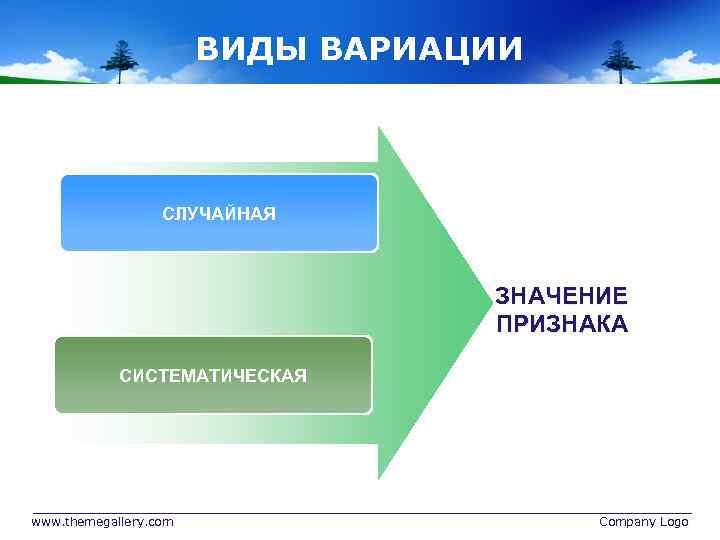 ВИДЫ ВАРИАЦИИ СЛУЧАЙНАЯ ЗНАЧЕНИЕ ПРИЗНАКА СИСТЕМАТИЧЕСКАЯ www. themegallery. com Company Logo
ВИДЫ ВАРИАЦИИ СЛУЧАЙНАЯ ЗНАЧЕНИЕ ПРИЗНАКА СИСТЕМАТИЧЕСКАЯ www. themegallery. com Company Logo
 Зачем изучать вариацию признака? 1. ЧТОБЫ ОЦЕНИТЬ степень зависимости признаков 2. ЧТОБЫ ОЦЕНИТЬ однородность совокупности по изучаемому признаку и доказать достоверность средней величины www. themegallery. com Company Logo
Зачем изучать вариацию признака? 1. ЧТОБЫ ОЦЕНИТЬ степень зависимости признаков 2. ЧТОБЫ ОЦЕНИТЬ однородность совокупности по изучаемому признаку и доказать достоверность средней величины www. themegallery. com Company Logo
 ПОКАЗАТЕЛИ ВАРИАЦИИ Для того чтобы измерить вариацию признака используют показатели (меры) вариации. www. themegallery. com Company Logo
ПОКАЗАТЕЛИ ВАРИАЦИИ Для того чтобы измерить вариацию признака используют показатели (меры) вариации. www. themegallery. com Company Logo
 АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ v Размах вариации (R) - абсолютная мера вариации признака, определяется как разность между наибольшим и наименьшим индивидуальными значениями признаков в совокупности: v Другим абсолютным показателем вариации является сумма квадратов отклонений (S): www. themegallery. com Company Logo
АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ v Размах вариации (R) - абсолютная мера вариации признака, определяется как разность между наибольшим и наименьшим индивидуальными значениями признаков в совокупности: v Другим абсолютным показателем вариации является сумма квадратов отклонений (S): www. themegallery. com Company Logo
 СРЕДНЕЕ ЛИНЕЙНОЕ ОТКЛОНЕНИЕ Среднее линейное отклонение характеризует среднюю ошибку (погрешность) в абсолютном выражении : www. themegallery. com Company Logo
СРЕДНЕЕ ЛИНЕЙНОЕ ОТКЛОНЕНИЕ Среднее линейное отклонение характеризует среднюю ошибку (погрешность) в абсолютном выражении : www. themegallery. com Company Logo
 ДИСПЕРСИЯ Для сравнения вариации совокупностей данных, имеющих разные единицы измерения, используют относительную меру вариации безразмерную величину дисперсию: www. themegallery. com Company Logo
ДИСПЕРСИЯ Для сравнения вариации совокупностей данных, имеющих разные единицы измерения, используют относительную меру вариации безразмерную величину дисперсию: www. themegallery. com Company Logo
 СВОЙСТВА ДИСПЕРСИИ 1. Если из всех значений вариант отнять какое-то постоянное число А, то дисперсия от этого не изменится. 2. Если все значения вариант разделить на какоето постоянное число А, то дисперсия уменьшится от этого в А 2 раз , а среднеквадратическое отклонение - в А раз. 3. Дисперсия от средней имеет свойство минимальности, т. е. она всегда меньше дисперсий, исчисленных от любых других величин. 4. Дисперсия равна разности среднего из квадратов и квадрата среднего: www. themegallery. com Company Logo
СВОЙСТВА ДИСПЕРСИИ 1. Если из всех значений вариант отнять какое-то постоянное число А, то дисперсия от этого не изменится. 2. Если все значения вариант разделить на какоето постоянное число А, то дисперсия уменьшится от этого в А 2 раз , а среднеквадратическое отклонение - в А раз. 3. Дисперсия от средней имеет свойство минимальности, т. е. она всегда меньше дисперсий, исчисленных от любых других величин. 4. Дисперсия равна разности среднего из квадратов и квадрата среднего: www. themegallery. com Company Logo
 Среднее квадратическое отклонение (σ) – стандартная ошибка среднего v равно корню квадратному из дисперсии v всегда больше среднего линейного отклонения v чем меньше среднее квадратическое отклонение, тем однороднее совокупность www. themegallery. com Company Logo
Среднее квадратическое отклонение (σ) – стандартная ошибка среднего v равно корню квадратному из дисперсии v всегда больше среднего линейного отклонения v чем меньше среднее квадратическое отклонение, тем однороднее совокупность www. themegallery. com Company Logo
 ОТНОСИТЕЛЬНЫЙ ПОКАЗАТЕЛЬ ВАРИАЦИИ Коэффициент вариации (V) : Если коэффициент вариации меньше 33%, то изучаемая совокупность однородна по исследуемому признаку и среднее значение может считаться состоятельной оценкой наиболее вероятного значения показателя. www. themegallery. com Company Logo
ОТНОСИТЕЛЬНЫЙ ПОКАЗАТЕЛЬ ВАРИАЦИИ Коэффициент вариации (V) : Если коэффициент вариации меньше 33%, то изучаемая совокупность однородна по исследуемому признаку и среднее значение может считаться состоятельной оценкой наиболее вероятного значения показателя. www. themegallery. com Company Logo
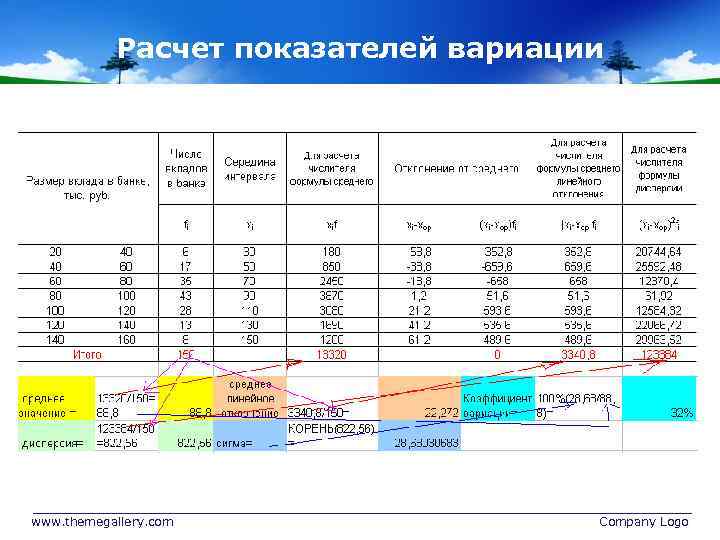 Расчет показателей вариации www. themegallery. com Company Logo
Расчет показателей вариации www. themegallery. com Company Logo
 ПРИМЕР ПРИМЕНЕНИЯ V В цеху в течение последнего месяца осуществлялись организационнотехнические мероприятия, которые должны привести к увеличению производительности труда. Необходимо оценить их эффективность. Для этого используем данные о средней выработке рабочих цеха : Номер декады Средняя выработка 1 рабочего за день, шт. www. themegallery. com 1 2 3 4 5 6 7 8 9 10 11 12 8 12 12 13 13 15 Company Logo
ПРИМЕР ПРИМЕНЕНИЯ V В цеху в течение последнего месяца осуществлялись организационнотехнические мероприятия, которые должны привести к увеличению производительности труда. Необходимо оценить их эффективность. Для этого используем данные о средней выработке рабочих цеха : Номер декады Средняя выработка 1 рабочего за день, шт. www. themegallery. com 1 2 3 4 5 6 7 8 9 10 11 12 8 12 12 13 13 15 Company Logo
 ПРИМЕР ПРИМЕНЕНИЯ V Сформулируем гипотезу Н 0 : проводимые мероприятия не ведут к увеличению производительности труда и изменения показателя средней выработки произошли в следствии действия случайных причин, то есть совокупность однородна по изучаемому признаку; Сформулируем гипотезу Н 1: проводимые мероприятия ведут к увеличению производительности труда, то есть совокупность неоднородна. Критическое значение критерия равно 33%. Рассчитаем эмпирическое значение критерия: хср = 11, 78 шт. ; = 1, 87; V=(1, 87 / 11, 78) 100%=15, 89% < 33% гипотеза Н 0 принимается, так как совокупность однородна. Таким образом, можно считать, что изменение показателей средней выработки лежит в пределах случайных колебаний, и не зависимо от проводимых мероприятий. www. themegallery. com Company Logo
ПРИМЕР ПРИМЕНЕНИЯ V Сформулируем гипотезу Н 0 : проводимые мероприятия не ведут к увеличению производительности труда и изменения показателя средней выработки произошли в следствии действия случайных причин, то есть совокупность однородна по изучаемому признаку; Сформулируем гипотезу Н 1: проводимые мероприятия ведут к увеличению производительности труда, то есть совокупность неоднородна. Критическое значение критерия равно 33%. Рассчитаем эмпирическое значение критерия: хср = 11, 78 шт. ; = 1, 87; V=(1, 87 / 11, 78) 100%=15, 89% < 33% гипотеза Н 0 принимается, так как совокупность однородна. Таким образом, можно считать, что изменение показателей средней выработки лежит в пределах случайных колебаний, и не зависимо от проводимых мероприятий. www. themegallery. com Company Logo
 ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ (РАЗЛИЧИЯ НАБЛЮДЕНИЙ) www. themegallery. com Company Logo
ПОКАЗАТЕЛИ ДИФФЕРЕНЦИАЦИИ (РАЗЛИЧИЯ НАБЛЮДЕНИЙ) www. themegallery. com Company Logo
 КВАНТИЛИ РАСПРЕДЕЛЕНИЯ Величины, характеризующие разбиение частотного распределения признака на ряд равных частей, обычно называют квантилями, которые являются ранговыми характеристиками распределения. www. themegallery. com Company Logo
КВАНТИЛИ РАСПРЕДЕЛЕНИЯ Величины, характеризующие разбиение частотного распределения признака на ряд равных частей, обычно называют квантилями, которые являются ранговыми характеристиками распределения. www. themegallery. com Company Logo
 ВИДЫ КВАНТИЛЕЙ квартили (Q), разбивающие распределение частот на четыре равные части, децили (D)(на 10 равных частей) процентили (P) (на 100 частей). www. themegallery. com Company Logo
ВИДЫ КВАНТИЛЕЙ квартили (Q), разбивающие распределение частот на четыре равные части, децили (D)(на 10 равных частей) процентили (P) (на 100 частей). www. themegallery. com Company Logo
 КВАРТИЛИ Квартилей всего три и Ме является вторым квартилем Q 2, так как делит совокупность данных 50% на 50% Первый квартиль Q 1 делит совокупность данных в соотношении 25% к 75% Третий квартиль Q 3 делит совокупность данных в соотношении 75% к 25% www. themegallery. com Company Logo
КВАРТИЛИ Квартилей всего три и Ме является вторым квартилем Q 2, так как делит совокупность данных 50% на 50% Первый квартиль Q 1 делит совокупность данных в соотношении 25% к 75% Третий квартиль Q 3 делит совокупность данных в соотношении 75% к 25% www. themegallery. com Company Logo
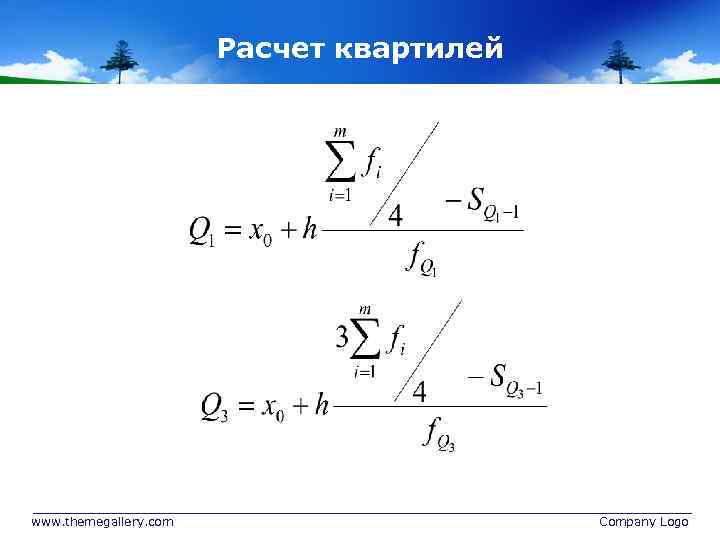 Расчет квартилей www. themegallery. com Company Logo
Расчет квартилей www. themegallery. com Company Logo
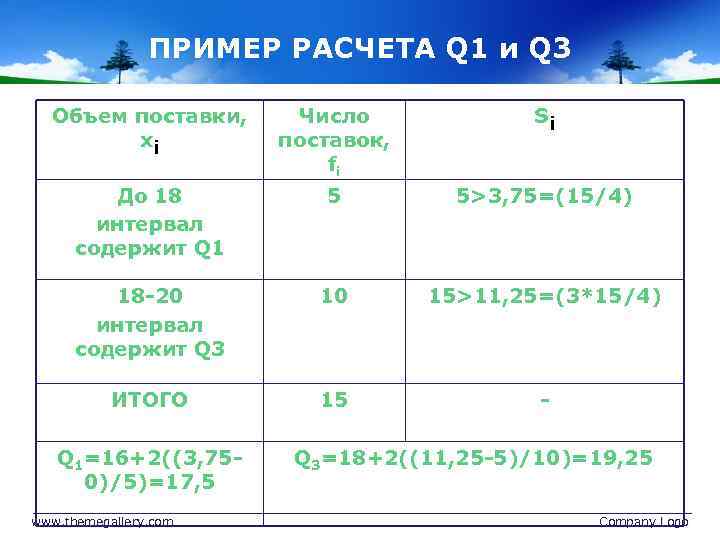 ПРИМЕР РАСЧЕТА Q 1 и Q 3 Объем поставки, хi Число поставок, fi Si До 18 интервал содержит Q 1 5 5>3, 75=(15/4) 18 -20 интервал содержит Q 3 10 15>11, 25=(3*15/4) ИТОГО 15 - Q 1=16+2((3, 750)/5)=17, 5 www. themegallery. com Q 3=18+2((11, 25 -5)/10)=19, 25 Company Logo
ПРИМЕР РАСЧЕТА Q 1 и Q 3 Объем поставки, хi Число поставок, fi Si До 18 интервал содержит Q 1 5 5>3, 75=(15/4) 18 -20 интервал содержит Q 3 10 15>11, 25=(3*15/4) ИТОГО 15 - Q 1=16+2((3, 750)/5)=17, 5 www. themegallery. com Q 3=18+2((11, 25 -5)/10)=19, 25 Company Logo
 Расчет децилей и персентилей www. themegallery. com Company Logo
Расчет децилей и персентилей www. themegallery. com Company Logo
 ПОКАЗАТЕЛИ (КОЭФФИЦИЕНТЫ) ДИФФЕРЕНЦИАЦИИ v Квартильная дифференциация KQ=Q 3/Q 1 v Децильная дифференциация КD=D 9/D 1 v Фондовая дифференциация Кф=(среднее из 10% наибольших величин)/(среднее из 10% наименьших величин) www. themegallery. com Company Logo
ПОКАЗАТЕЛИ (КОЭФФИЦИЕНТЫ) ДИФФЕРЕНЦИАЦИИ v Квартильная дифференциация KQ=Q 3/Q 1 v Децильная дифференциация КD=D 9/D 1 v Фондовая дифференциация Кф=(среднее из 10% наибольших величин)/(среднее из 10% наименьших величин) www. themegallery. com Company Logo
 АССИМЕТРИЯ Симметричность распределения признака характеризует коэффициент ассиметрии: As=μ 3/σ³, где μ 3 = центральный момент распределения 3 -го порядка σ³ - среднее квадратическое отклонение в кубе ЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, ТО ЕСТЬ ПОДЧИНЯЮТСЯ РАСПРЕДЕЛЕНИЮ Гаусса, то они имеют симметричное распределение признака, когда As=0 или |As|/σAS<3, где σAS= www. themegallery. com Company Logo
АССИМЕТРИЯ Симметричность распределения признака характеризует коэффициент ассиметрии: As=μ 3/σ³, где μ 3 = центральный момент распределения 3 -го порядка σ³ - среднее квадратическое отклонение в кубе ЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, ТО ЕСТЬ ПОДЧИНЯЮТСЯ РАСПРЕДЕЛЕНИЮ Гаусса, то они имеют симметричное распределение признака, когда As=0 или |As|/σAS<3, где σAS= www. themegallery. com Company Logo
 ЭКСЦЕСС ( «горб» ) Высоту «горба» распределения, его крутизну характеризует показатель эксцесса: Ех = (µ 4/σ4)-3, где центральный момент распределения 4 -го порядка μ 4 = , σ4 - дисперсия в квадрате ЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, ТО ЕСТЬ ПОДЧИНЯЮТСЯ РАСПРЕДЕЛЕНИЮ Гаусса, то они имеют такой «горб» , когда Ех=0 ( µ 4/σ =3) или |Ех|/σЕх<3, где σЕх= www. themegallery. com Company Logo
ЭКСЦЕСС ( «горб» ) Высоту «горба» распределения, его крутизну характеризует показатель эксцесса: Ех = (µ 4/σ4)-3, где центральный момент распределения 4 -го порядка μ 4 = , σ4 - дисперсия в квадрате ЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, ТО ЕСТЬ ПОДЧИНЯЮТСЯ РАСПРЕДЕЛЕНИЮ Гаусса, то они имеют такой «горб» , когда Ех=0 ( µ 4/σ =3) или |Ех|/σЕх<3, где σЕх= www. themegallery. com Company Logo
 НОРМАЛЬНЫЕ ДАННЫЕ правило трех сигм ЕСЛИ В СОВОКУПНОСТИ ВСЕ ВАРИАНТЫ НАХОДЯТСЯ В ИНТЕРВАЛЕ , ТО ОНИ НОРМАЛЬНЫЕ www. themegallery. com Company Logo
НОРМАЛЬНЫЕ ДАННЫЕ правило трех сигм ЕСЛИ В СОВОКУПНОСТИ ВСЕ ВАРИАНТЫ НАХОДЯТСЯ В ИНТЕРВАЛЕ , ТО ОНИ НОРМАЛЬНЫЕ www. themegallery. com Company Logo
 АНОМАЛЬНЫЕ ДАННЫЕ ВЫБРОСЫ ЕСЛИ В СОВОКУПНОСТИ ЕСТЬ ВАРИАНТЫ, КОТОРЫЕ НАХОДЯТСЯ ЗА ПРЕДЕЛАМИ ИНТЕРВАЛА , ТО ОНИ АНОМАЛЬНЫЕ www. themegallery. com Company Logo
АНОМАЛЬНЫЕ ДАННЫЕ ВЫБРОСЫ ЕСЛИ В СОВОКУПНОСТИ ЕСТЬ ВАРИАНТЫ, КОТОРЫЕ НАХОДЯТСЯ ЗА ПРЕДЕЛАМИ ИНТЕРВАЛА , ТО ОНИ АНОМАЛЬНЫЕ www. themegallery. com Company Logo
 РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
 РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
 РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
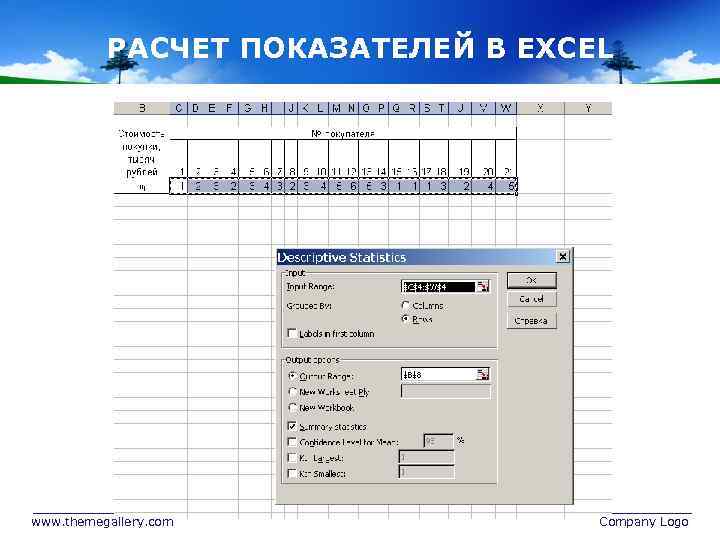 РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
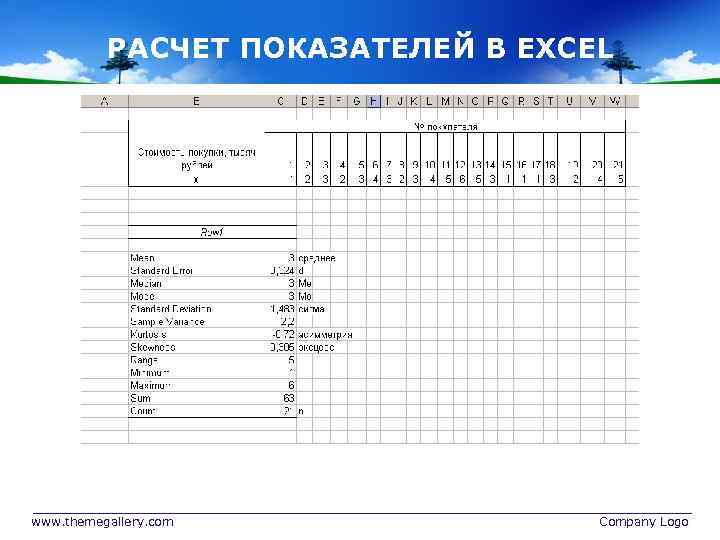 РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL www. themegallery. com Company Logo
 LOGO www. themegallery. com
LOGO www. themegallery. com


