LOGIT PROBIT.pptx
- Количество слайдов: 36

Logit и Probit МУП 151, 152 ВЛАДИМИР ГЛАЗУНОВ ГРИГОРИЙ САВИЦКИЙ ДМИТРИЙ КИБАНОВ

Logit

Применение логистической регрессии §Есть много важных исследовательских тем, для которых зависимая переменная является "ограниченной". §Например: голосования, учет заболеваемости или смертности не могут быть описаны непрерывным или нормальным распределением. §Бинарная логистическая регрессия- это тип регрессионного анализа, где зависимой переменной является фиктивная переменная, кодированная нулем (событие не произошло) или единицей (произошло) 3

Линейная вероятностная модель В регрессии МНК: Y = β 0 + β 1 X + e ; где Y = (0, 1) §Значения ошибок - гетероскедастичные §е не подчиняется нормальному распределению, т. к. Y принимает только два значения §Предсказанные вероятности могут быть больше единицы или меньше нуля 4
![Логистическая регрессионная модель Модель «логит» решает эти проблемы: ln[p/(1 -p)] = 0 + 1 Логистическая регрессионная модель Модель «логит» решает эти проблемы: ln[p/(1 -p)] = 0 + 1](https://present5.com/presentation/-100577472_437014721/image-5.jpg)
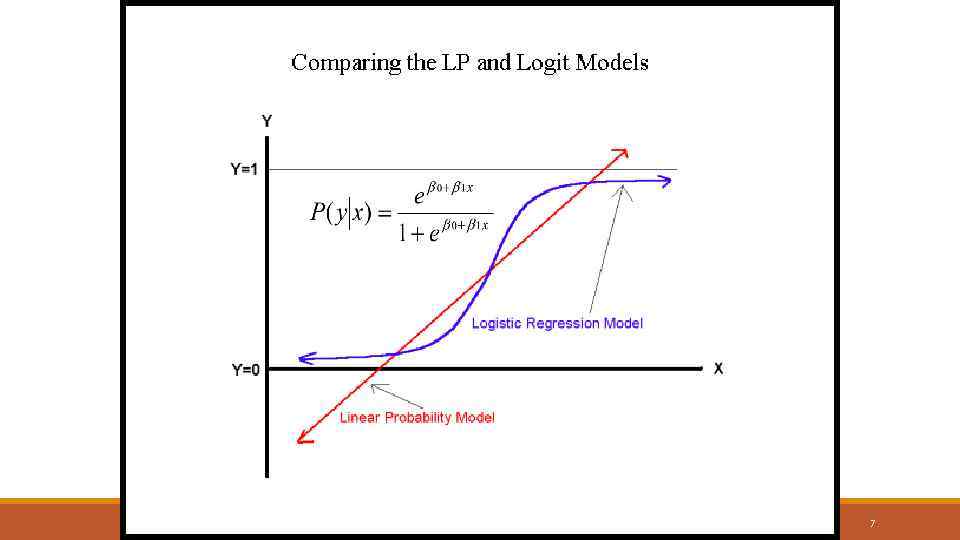
Логистическая регрессионная модель Модель «логит» решает эти проблемы: ln[p/(1 -p)] = 0 + 1 X §p –вероятность, что событие Y произойдет, p(Y=1) § [диапазон=0 to 1] §p/(1 -p) - это «отношение вероятностей» § [диапазон =0 to ∞] §ln[p/(1 -p)]- «логит» § [диапазон=-∞ to +∞] 5
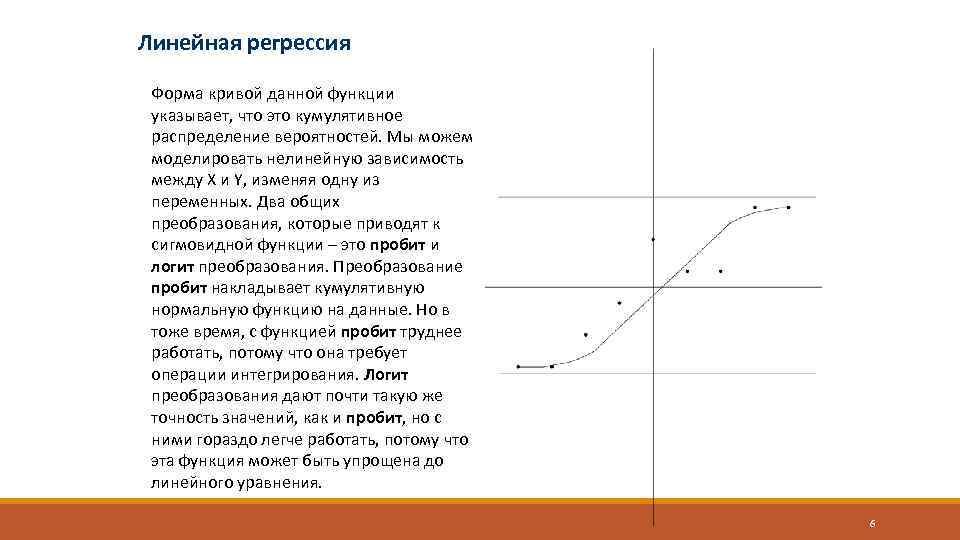
Линейная регрессия Форма кривой данной функции указывает, что это кумулятивное распределение вероятностей. Мы можем моделировать нелинейную зависимость между X и Y, изменяя одну из переменных. Два общих преобразования, которые приводят к сигмовидной функции – это пробит и логит преобразования. Преобразование пробит накладывает кумулятивную нормальную функцию на данные. Но в тоже время, с функцией пробит труднее работать, потому что она требует операции интегрирования. Логит преобразования дают почти такую же точность значений, как и пробит, но с ними гораздо легче работать, потому что эта функция может быть упрощена до линейного уравнения. 6
7

Отношение вероятностей Логистическая функция определяется как логарифм отношения вероятностей: Это преобразование является полезным, поскольку он создает переменную с диапазоном от - до +. Тем самым, оно решает проблему ограниченного диапазона вероятности (зависимой переменной) – от 0 до 1 -, поскольку диапазон логит-функции не ограничен. К тому же значения легко интерпретировать - достаточно посчитать экспоненту. 8
![Тестирование гипотезы §Тест Вальда для коэффициента : Wald = [ /s. e. B]2 описывается Тестирование гипотезы §Тест Вальда для коэффициента : Wald = [ /s. e. B]2 описывается](https://present5.com/presentation/-100577472_437014721/image-9.jpg)
Тестирование гипотезы §Тест Вальда для коэффициента : Wald = [ /s. e. B]2 описывается распределением хи-квадрат с 1 степенью свободы. 9

Probit

Введение в пробит Линейная оценка параметров (базовая эконометрика): В большинстве случаев, в подобных уравнениях Y, т. е. наша зависимая переменная, является непрерывной Суть методов, основанных на логит и пробит-регрессиях, заключается в наличии дихотомичного Y (делящегося на две части) Они возникают во многих реальных жизненных ситуациях: ◦ Подсчет голосов – да/нет ◦ Участие в военных конфликтах – участвовал/не участвовал

Связующие функции служат для связи между фактическим Y и рассчитываемым в эконометрической модели Пример c логарифмами: ◦ Анализируем связующую функцию по методу МНК (метод наименьших квадратов) ◦ Для справки: МНК - математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.

Графическое изображений дихотомичного Y Пример с выбором меньшинств в законодательные органы одного из штатов США (0 – не из числа меньшинств; 1 – из числа меньшинств)
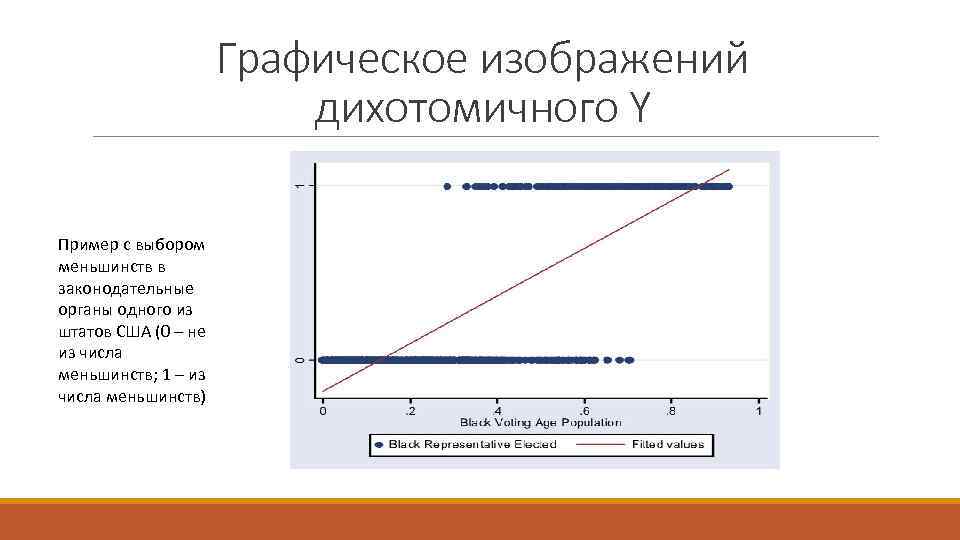
Графическое изображений дихотомичного Y Пример с выбором меньшинств в законодательные органы одного из штатов США (0 – не из числа меньшинств; 1 – из числа меньшинств)

Решение проблемы Необходимо превратить дихотомичный Y в непрерывную переменную, с помощью связующей функции Y’
![Вопрос Какая функция F(Y) может находится в интервале от [0; 1] и отвечать требуемым Вопрос Какая функция F(Y) может находится в интервале от [0; 1] и отвечать требуемым](https://present5.com/presentation/-100577472_437014721/image-16.jpg)
Вопрос Какая функция F(Y) может находится в интервале от [0; 1] и отвечать требуемым критериям? ◦ Результаты вычислений по этим функциям (т. е. наша вероятность) должны находиться в интервале от 0 до 1 Подсказка: функция должна быть взята наоборот, т. е. в степени ^(-1)

Нормальное распределение, как связующая функция при Это и есть пробит-функция
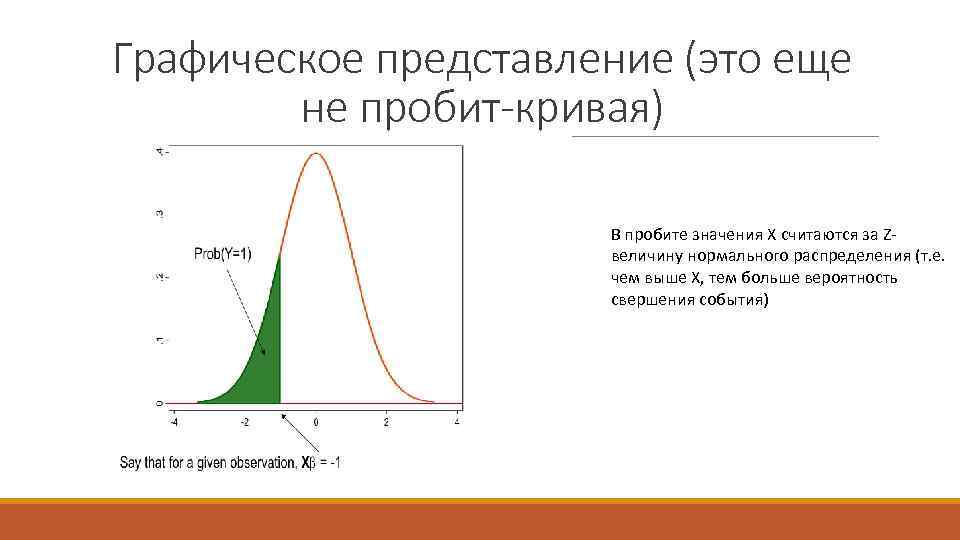
Графическое представление (это еще не пробит-кривая) В пробите значения X считаются за Zвеличину нормального распределения (т. е. чем выше X, тем больше вероятность свершения события)
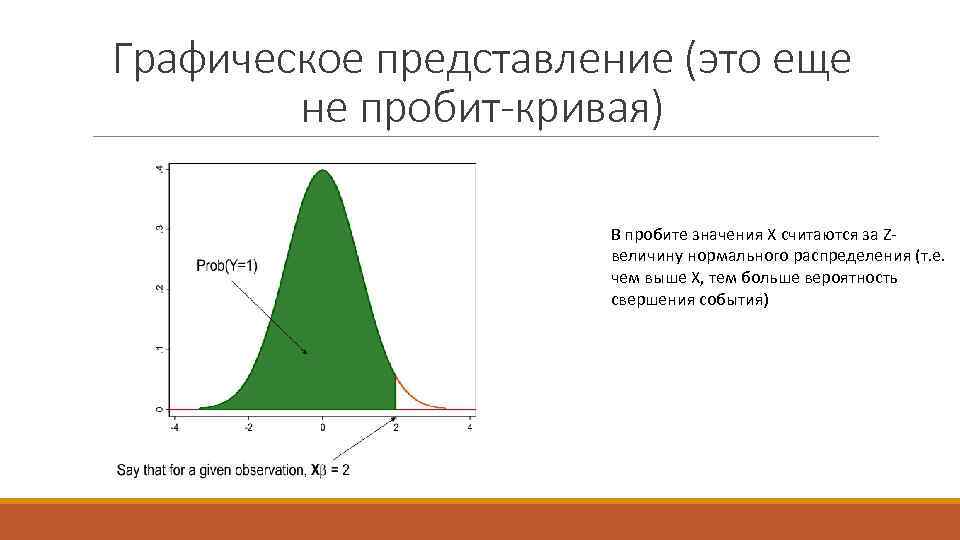
Графическое представление (это еще не пробит-кривая) В пробите значения X считаются за Zвеличину нормального распределения (т. е. чем выше X, тем больше вероятность свершения события)
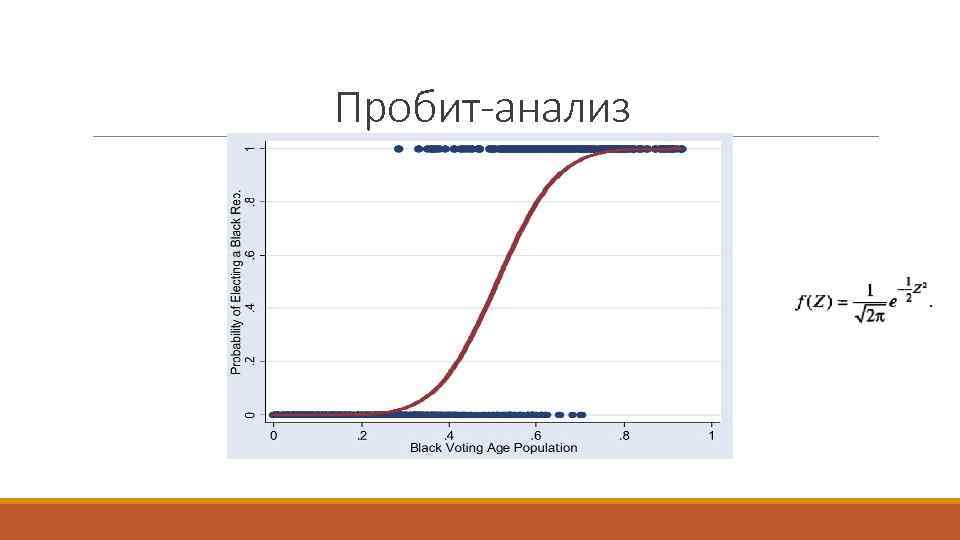
Пробит-анализ
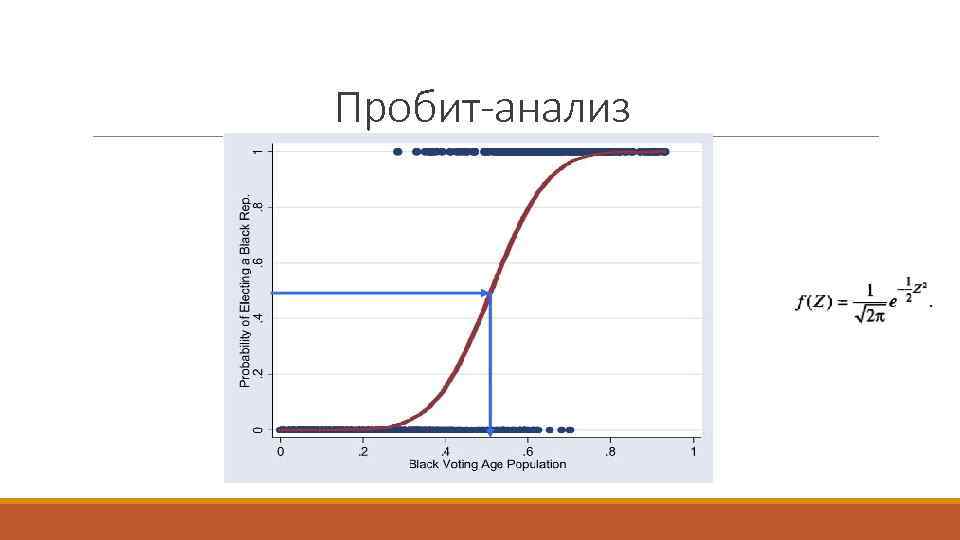
Пробит-анализ

Метод максимального правдоподобия Допустим, мы оцениваем с помощью пробит-анализа и у нас есть некие тестовые коэффициенты Тогда для каждого наблюдаемого yi, у нас есть xi и свое , тогда имеем Таким образом мы можем сказать, для примера, , что , тогда имеем правдоподобие свершения данного события равное 0, 8.
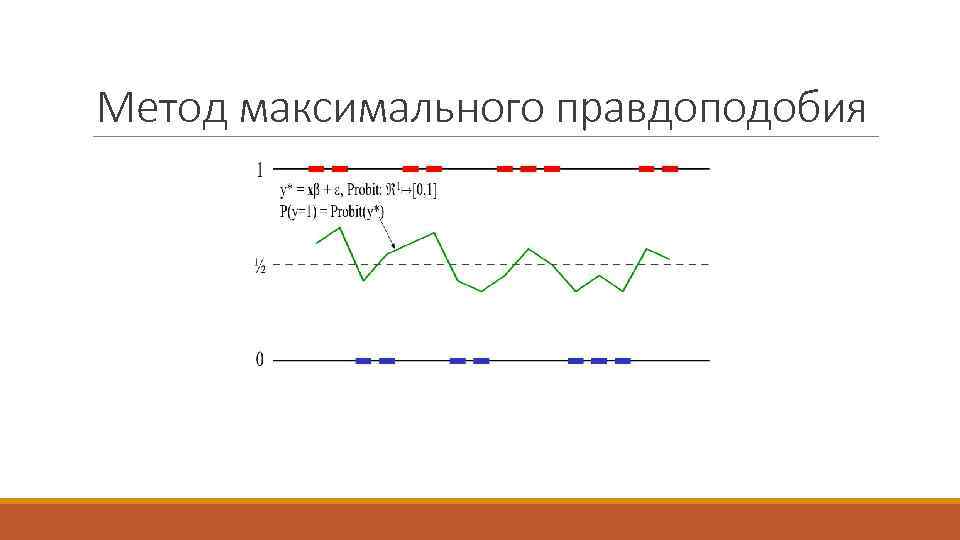
Метод максимального правдоподобия

Пример

Убить 50% нематодов Задача – найти LC 50 - % раствора убивающий 50% нематодов

Корректировка доли необходима, чтобы избавиться от нематод, умерших не из-за раствора Рассматриваются только 3 эксперимента с наиболее приближенным результатом из-за высокой неопределенности и нелинейности

Logit необходим, чтобы линеаризировать информацию - привести модели с нелинейной спецификацией к линейной, чтобы можно было применять статистические методы
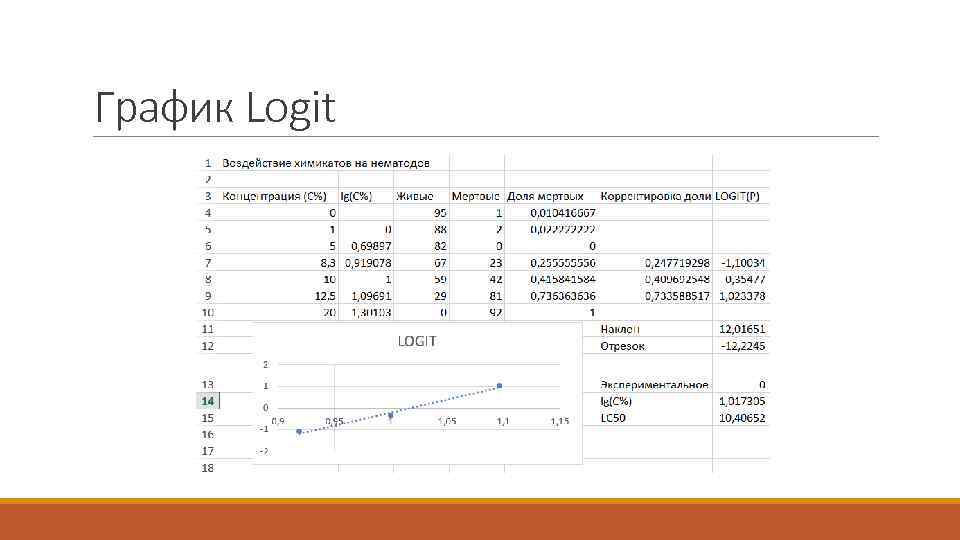
График Logit
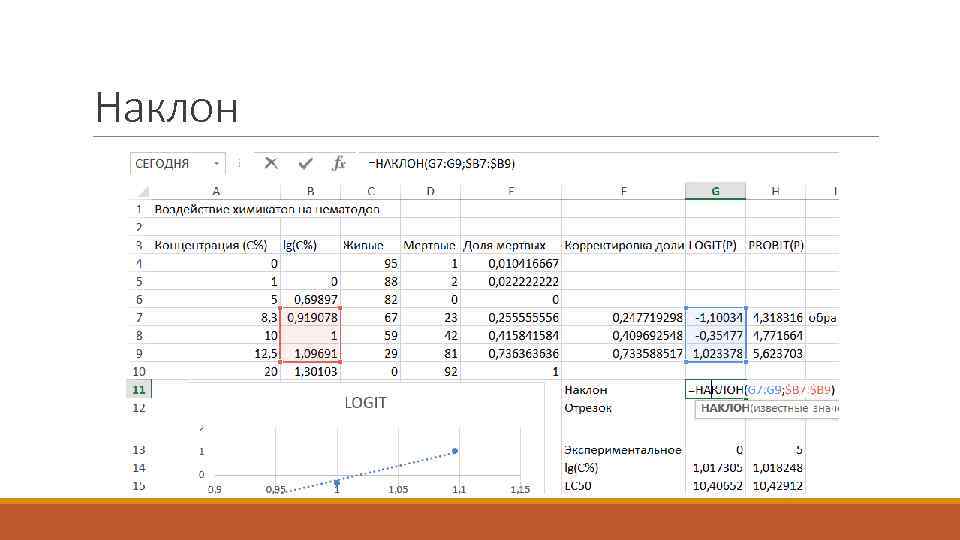
Наклон
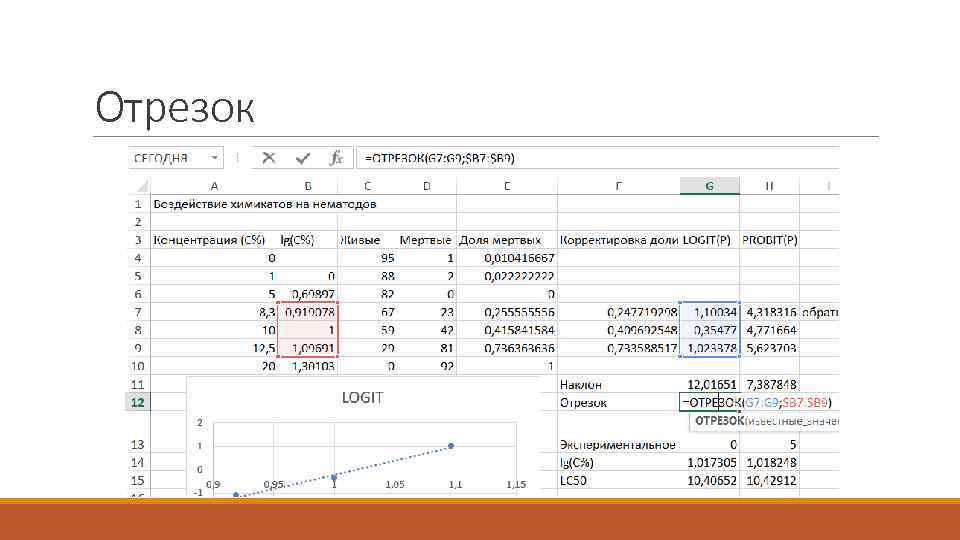
Отрезок
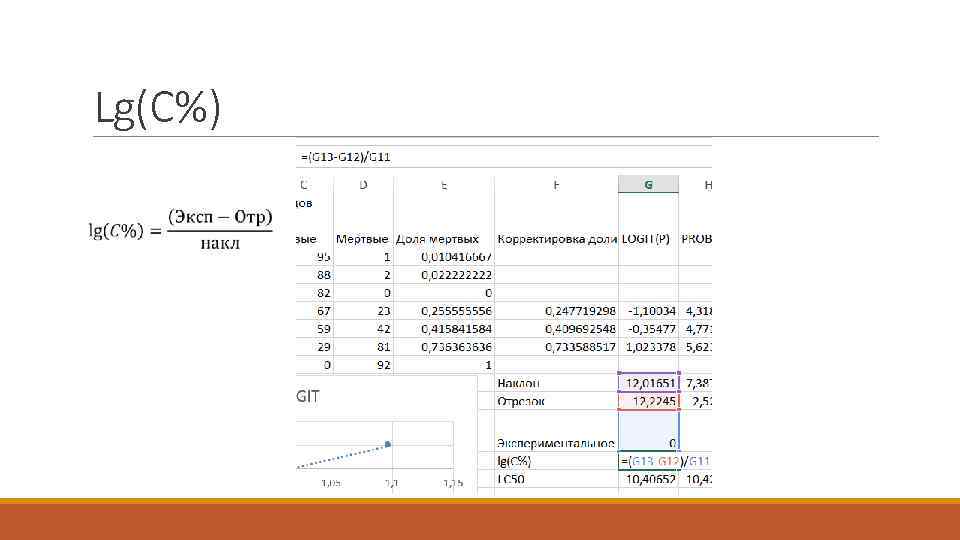
Lg(C%)

LC 50
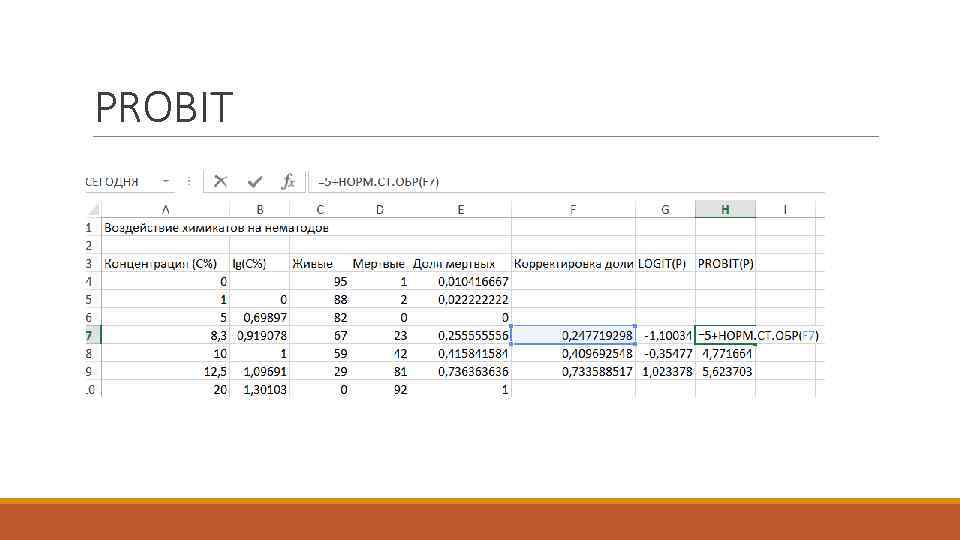
PROBIT
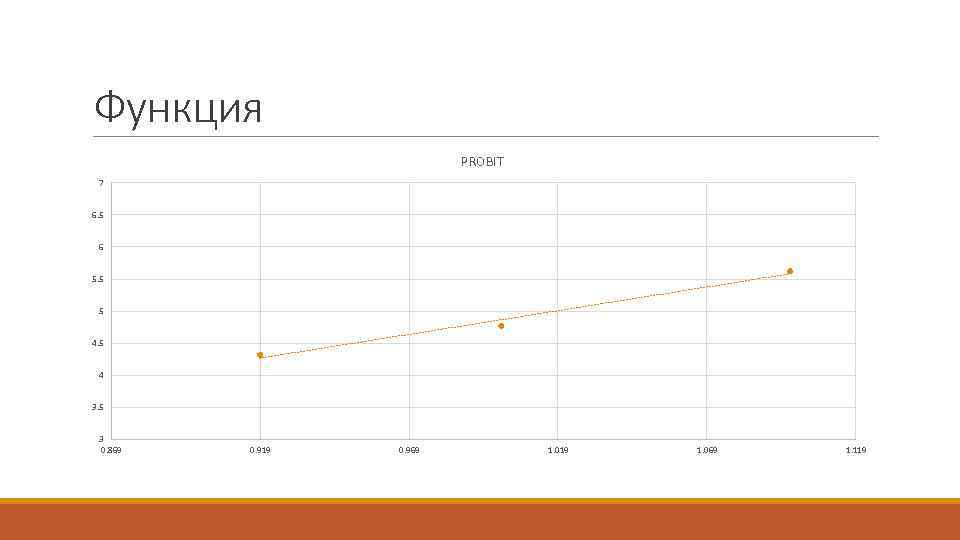
Функция PROBIT 7 6. 5 6 5. 5 5 4 3. 5 3 0. 869 0. 919 0. 969 1. 019 1. 069 1. 119
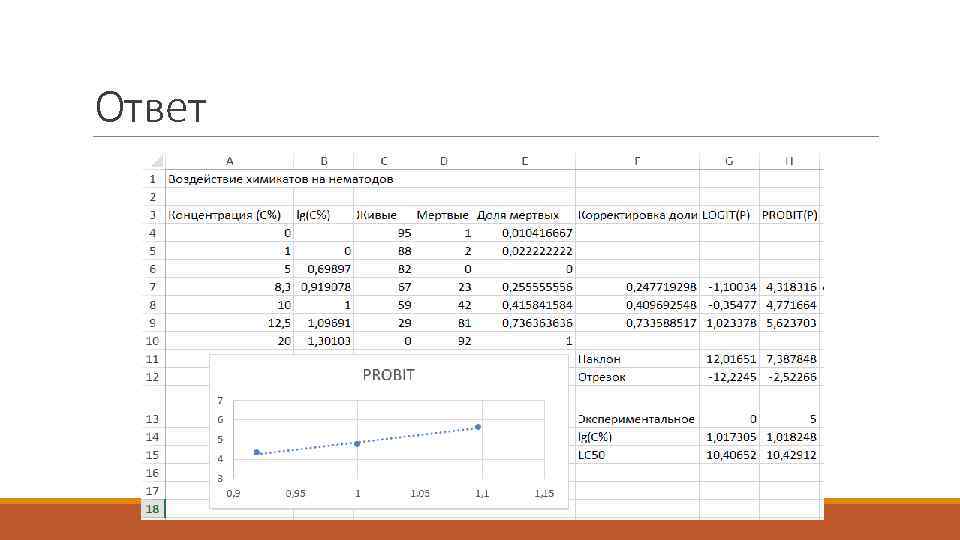
Ответ

Ссылки http: //personal. ecu. edu/whiteheadj/data/logit/ ◦ http: //www. math. yorku. ca/SCS/Courses/grcat/grc 6. html ◦ http: //www. ats. ucla. edu/stat/sas/seminars/sas_logistic/logistic 1. htm ◦ http: //www. pauldickman. com/teaching/sas_logistic_seminar 8. pdf
LOGIT PROBIT.pptx