ЛОГИКА Соснин Пётр Иванович Лекции Практические занятия Экзамен

ЛОГИКА Соснин Пётр Иванович Лекции Практические занятия Экзамен

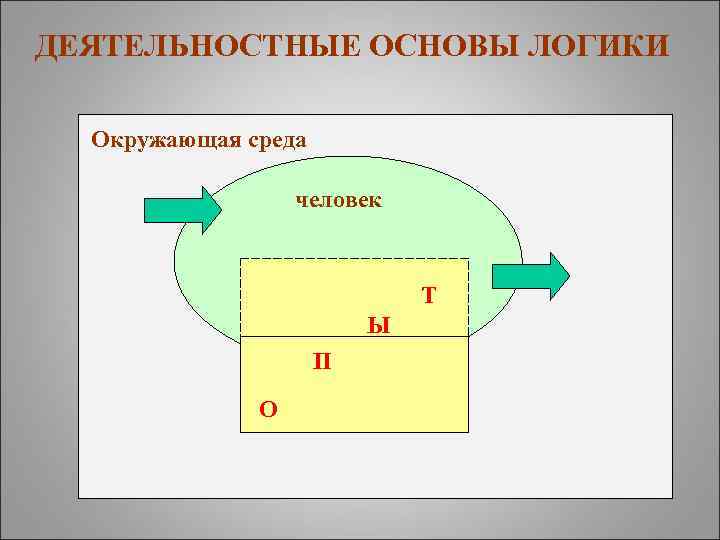ДЕЯТЕЛЬНОСТНЫЕ ОСНОВЫ ЛОГИКИ Окружающая среда человек Т Ы П О

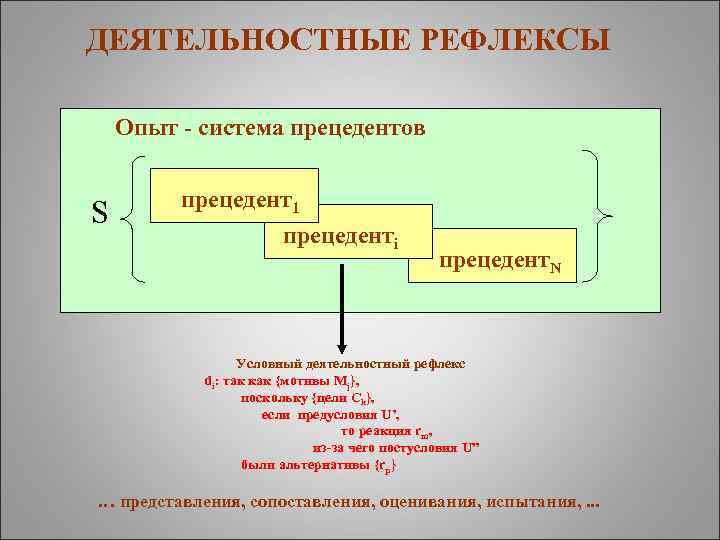ДЕЯТЕЛЬНОСТНЫЕ РЕФЛЕКСЫ Опыт - система прецедентов S прецедент1 прецедентi прецедент. N Условный деятельностный рефлекс di: так как {мотивы Mj}, поскольку {цели Ck}, если предусловия U’, то реакция rm, из-за чего постусловия U” были альтернативы {rp} … представления, сопоставления, оценивания, испытания, . . .

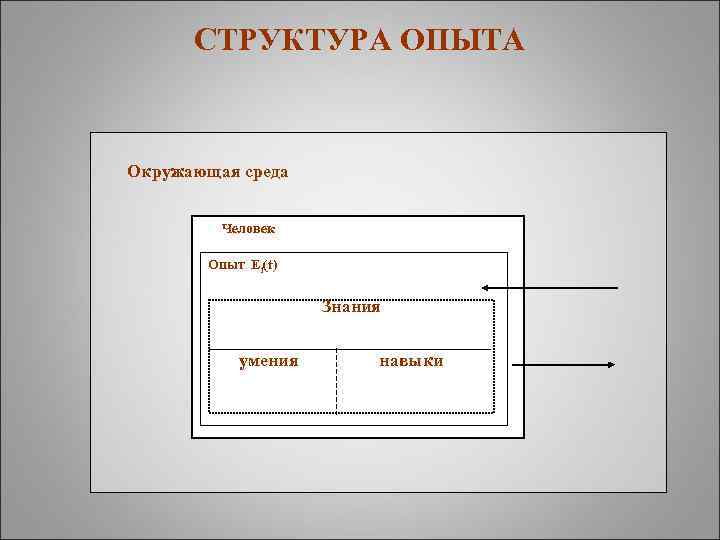СТРУКТУРА ОПЫТА Окружающая среда Человек Опыт Ei(t) Знания умения навыки

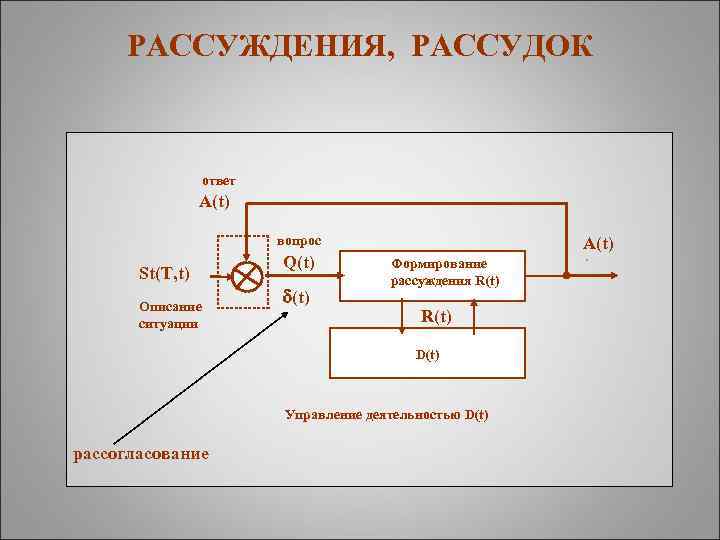РАССУЖДЕНИЯ, РАССУДОК ответ A(t) вопрос St(T, t) Описание ситуации Q(t) A(t) Формирование рассуждения R(t) D(t) Управление деятельностью D(t) рассогласование

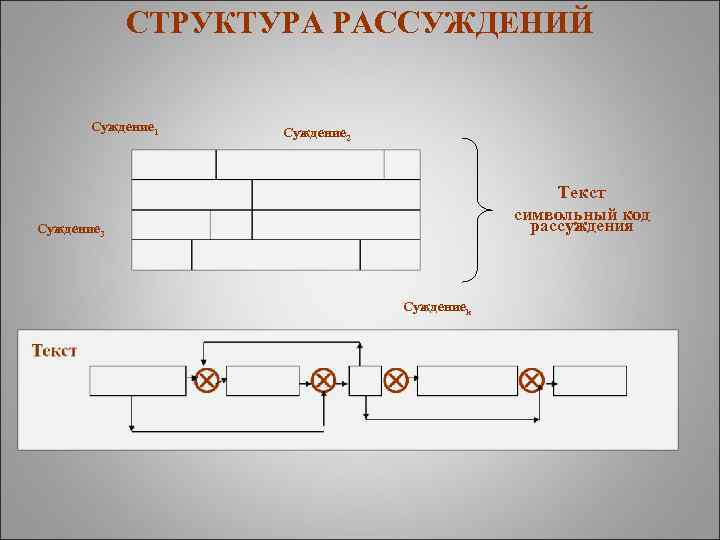СТРУКТУРА РАССУЖДЕНИЙ Суждение 1 Суждение 2 Текст символьный код рассуждения Суждение 3 Суждениеk

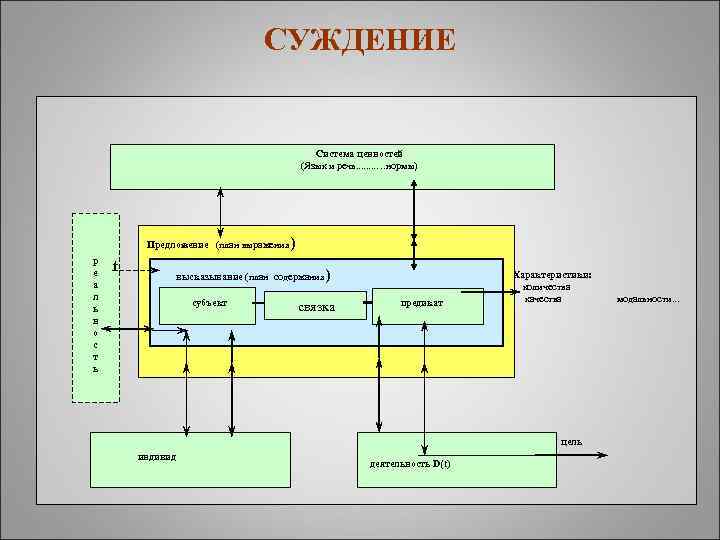СУЖДЕНИЕ Система ценностей (Язык и речь. . . . …нормы) Предложение (план выражения р е а л ь н о с т ь t ) высказывание (план содержания субъект ) связка предикат Характеристики: количества качества цель индивид деятельность D(t) модальности. . .

ТРИ ТЕОРИИ ИСТИНЫ В СОВРЕМЕННОЙ ЛОГИКЕ • Теория соответствия: истинность есть соответствие фактам: w m. • Теория согласованности (когерентности): высказывание считается истинным, если оно согласуется с остальной частью нашего знания: m m* • Теория полезности: истинность есть прагматическая пригодность или полезность. Правдоподобность – это приближение к истине. Уверенность – достижение требуемого уровня истинности

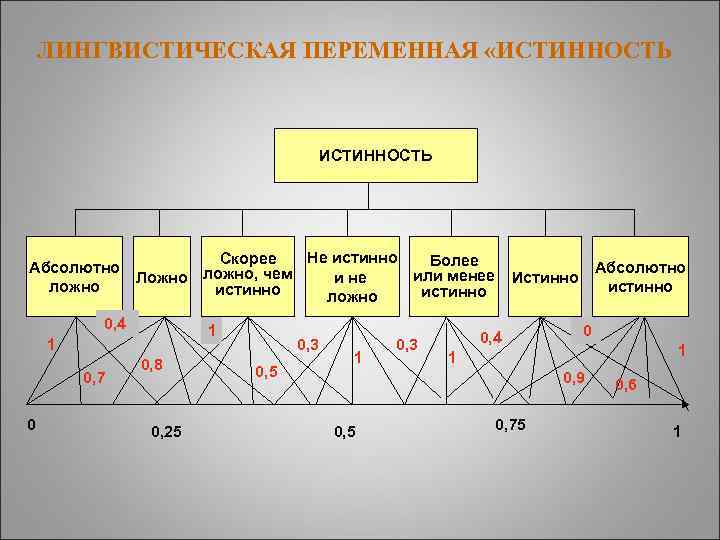ЛИНГВИСТИЧЕСКАЯ ПЕРЕМЕННАЯ «ИСТИННОСТЬ Не истинно Скорее Более Абсолютно ложно, чем или менее и не Ложно ложно истинно ложно 0, 4 1 1 0, 7 0 0, 8 0, 25 0, 3 0, 5 1 0, 3 Абсолютно истинно Истинно 0, 4 0 1 1 0, 9 0, 5 0, 75 0, 6 1

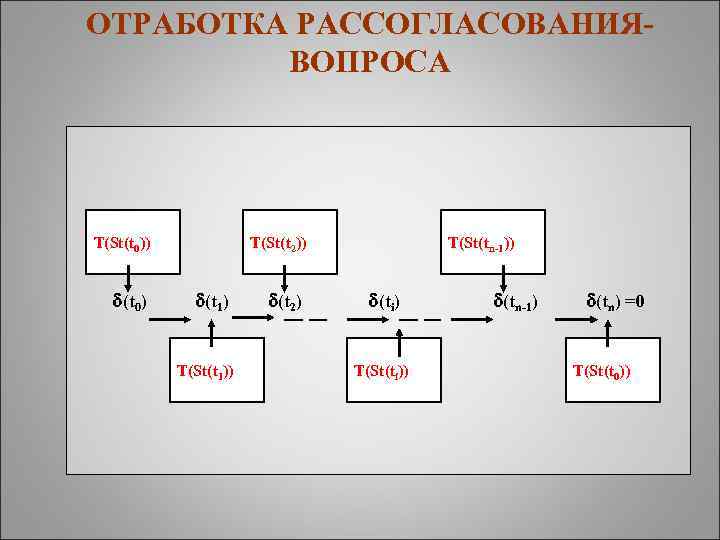ОТРАБОТКА РАССОГЛАСОВАНИЯВОПРОСА T(St(t 0)) (t 0) T(St(t 2)) (t 1) T(St(t 1)) (t 2) T(St(tn-1)) (ti) T(St(ti)) (tn-1) (tn) =0 T(St(t 0))

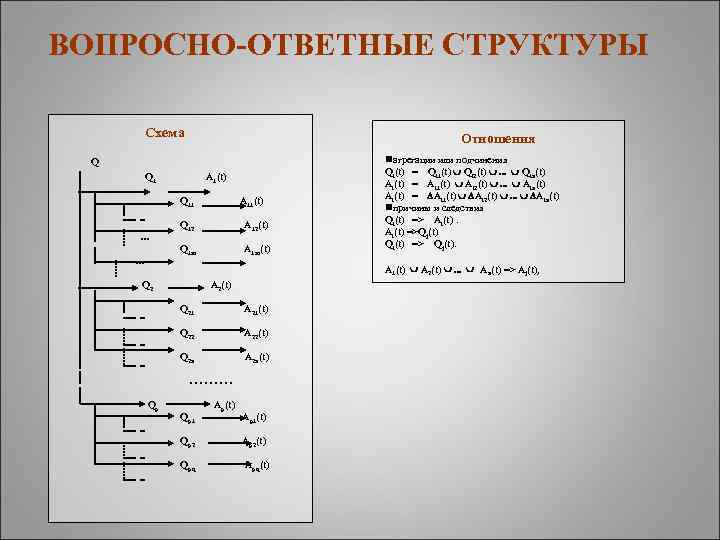ВОПРОСНО-ОТВЕТНЫЕ СТРУКТУРЫ Схема Отношения Q Q 1 A 1(t) Q 11 A 11(t) … Q 12 A 12(t) Q 1 m … A 1 m(t) nагрегации или подчинения Qi(t) = Qi 1(t) Qi 2(t) . . . Qin(t) Ai(t) = Ai 1(t) Ai 2(t) . . . Ain(t) Ai(t) = Ai 1(t) Ai 2(t) . . . Ain(t) nпричины и следствия Qi(t) => Ai(t) =>Qj(t) Qi(t) => Qj(t). A 1(t) A 2(t) . . . An(t) => Aj(t), Q 2 A 2(t) Q 21 A 21(t) Q 22 A 22(t) Q 2 n A 2 n(t) . . Qp Qp 1 Qp 2 Qpq Ap(t) Ap 1(t) Ap 2(t) Apq(t)

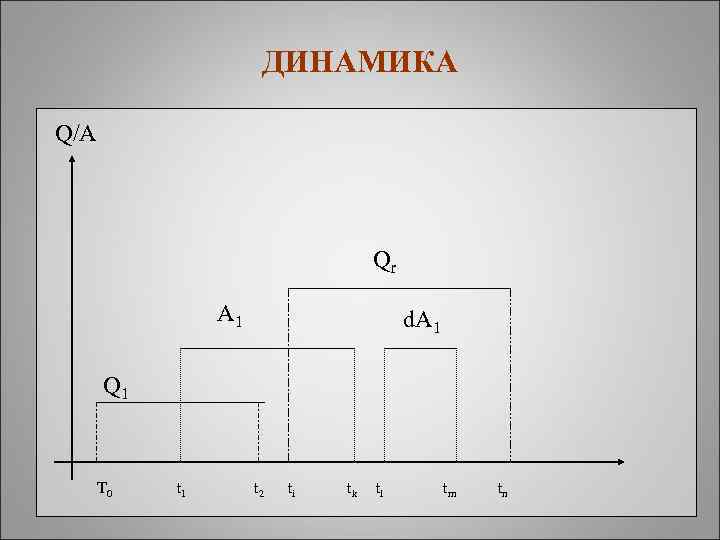ДИНАМИКА Q/A Qr A 1 d. A 1 Q 1 T 0 t 1 t 2 ti tk tl tm tn

ЧТО ЕСТЬ ЛОГИКА? 1. Логика – это наука о человеческом мышлении, его законах и формах 2. Логика – это наука о правильных рассуждениях (законах, правилах и нормах корректных рассуждений) 3. Логика – это наука об искусственных средствах оперирования языком (А. А. Зиновьев), специальная теория искусственных языковых систем 4. Логика – это наука о наиболее общих законах существования истины (Г. Фреге)

ЧТО ЕСТЬ ЛОГИКА? (продолжение) По Я. Лукасевичу, логика есть наука об истинностных значениях. «Все истинные высказывания обозначают один и тот же объект, а именно, истину, и все ложные высказывания обозначают один и тот же объект, а именно, ложь. Я рассматриваю истину и ложь как единичные (сингулярные) объекты. Онтологическим аналогом истины является бытие, а лжи – небытие. Объекты, обозначаемые высказываниями, называются логическими значениями. Логика есть наука об особого рода объектах, а именно, наука о логических значениях» .

ФУНКЦИИ ЛОГИКИ В ТЕОРИИ И ПРИЛОЖЕНИЯХ ИСКУССТВЕННОГОИНТЕЛЛЕКТА 1. ЛОГИКА КАК ОСНОВА ПРЕДСТАВЛЕНИЯ ЗНАНИЙ И ФОРМАЛИЗАЦИИ РАССУЖДЕНИЙ 2. ЛОГИКА КАК ИНСТРУМЕНТ ИССЛЕДОВАНИЯ ЕСТЕСТВЕННОГО ЯЗЫКА 3. ЛОГИКА КАК ЯЗЫК ПРОГРАММИРОВАНИЯ

НОВЫЕ ФУНКЦИИ ЛОГИКИ В ИСКУССТВЕННОМ ИНТЕЛЛЕКТЕ I. Логика как «формальная философия» (А. С. Карпенко) для изучения интеллекта на всех уровнях (индивидуальный, коллективный, организационный интеллект) Например, многозначные и нечеткие логики выступают как средства описания неопределенности, неполноты, противоречивости, неточности, нечеткости имеющейся информации II. Логики как средства поддержки разработки прикладных интеллектуальных систем (в особенности, многоагентных систем)

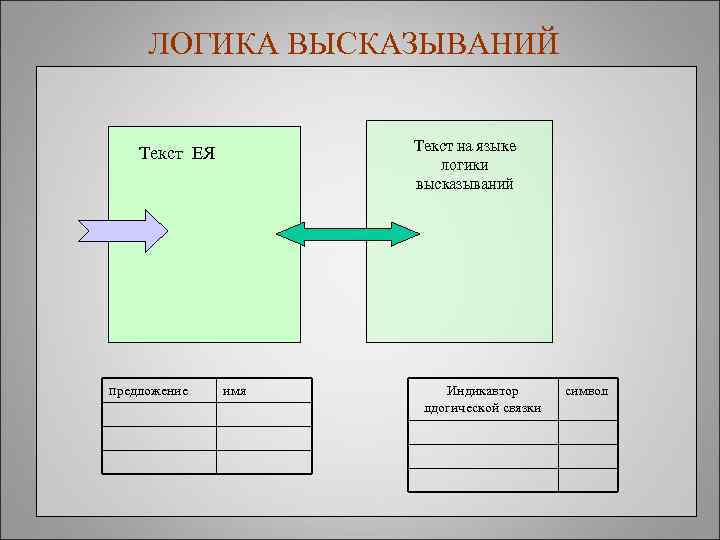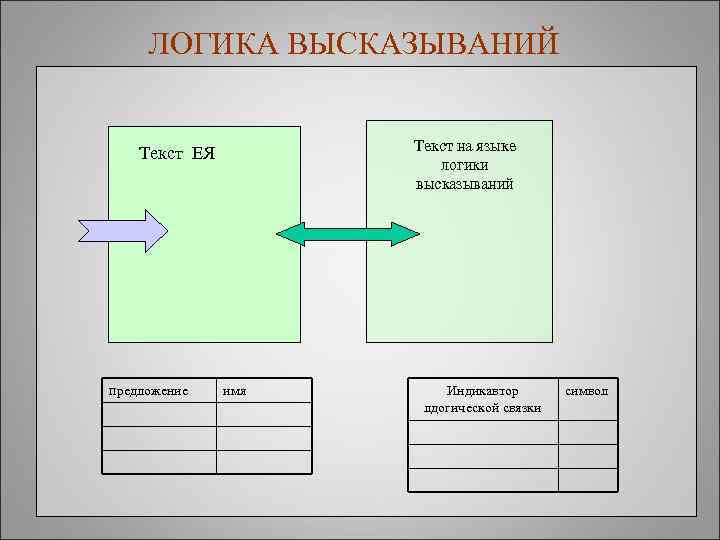ЛОГИКА ВЫСКАЗЫВАНИЙ Текст на языке логики высказываний Текст ЕЯ предложение имя Индикавтор лдогической связки символ

ЛОГИКА ВЫСКАЗЫВАНИЙ Текст на языке логики высказываний Текст ЕЯ предложение имя Индикавтор лдогической связки символ

ЛОГИКА ВЫСКАЗЫВАНИЙ Текст на языке логики высказываний Текст ЕЯ предложение имя Индикавтор лдогической связки символ

ЗАКОНЫ Закон тождества Закон непротиворечия Закон исключённого третьего Закон достаточного основания А есть А Неверно, что А и не А А ест ь либо В либо не В Если есть В, то есть и его основание А А –> A - (A ->-A) -(-A-> A) (A+ -A) A->(B->A)

ЗАКОНЫ тождества A<->A = (A ->A)&(A->A) = A->A = -A+A = 1 противоречия - (A&-A) = -A+A = 1; -(A->-A) = -(-A+(-A)) = -A ? ? исключённого третьего A+(-A) = 1 достаточного основания A->(B->A) где А? ? и насколько оно убеждает A 1/A 2/… /An/ - если присоединить к аргументам ещё и An, то степень убедительности окажется достаточной An A 2 A 1 t 2 tn t убеждённость = убедительность (определённой степени) + вера

ЗАКОНЫ двойного отрицания --A = A коммутативности A&B = B&A, A+B = B+A ассоциативности (A&B) &C = A&(B&C) , (A+B)+C = A+(B+C) дистрибутивности A+ B&C = (A+B)&(A+C), де Моргана -(A+B) = -A & (-B) , -(A&B) = -A+(-B) контрапозиции (A->B) -> (-A ->(-B)), модус поненс (A->B)&A -> приведения к абсурду другие……. A&(B+C) = A&B + A&C (-A ->(-B)) -> (A->B) , (A ->(-B)) -> (B->(-A)) B (A->B) & (A-> (-B)) -> -A

ВЫВОД И ДОКАЗАТЕЛЬСТВО АКСИОМЫ + ЗАКОНЫ ТЕОРЕМЫ СИНТАКСИЧЕСКИ ПРАВИЛЬНЫЕ ФОРМУЛЫ СИМВОЛИЧЕСКИ ПОСТРОЕННЫЕ ФОРМЫ