Логика предикатов Логика предикатов n Логика предикатов

Логика предикатов

Логика предикатов n Логика предикатов представляет собой развитие логики высказываний. n С помощью логики высказываний можно описать и исследовать структуру сложных высказываний. Установить их истинность или ложность в зависимости от истинностных значений входящих в нее простых высказываний n Предикат используется для описания внутренней логической структуры простых высказываний (т. е. высказываний не содержащих связок)

Определение предиката n Предикат – повествовательное предложение, содержащее предметные переменные, определенные на соответствующих множествах n Например: P(x, y)= «Студент x на экзамене получил отметку y» . Переменные x, y являются предметными и принадлежат следующим множествам x={Иванов, Петров, Сидоров}, y={2, 3, 4, 5}. n При замене переменных конкретными значениями (элементами множеств) предикат обращается в высказывание т. е. принимает значение «истинно» или «ложно» . Например: «Студент Иванов на экзамене получил отметку 5» n Предикатом P(x 1, …, xn) зависящим от n переменных называется функция P: M 1 M 2 … Mn B, где Mi — произвольные множества, а B — двоичное множество. При этом предполагается, что xi Mi. n M 1, M 2, …, Mn – предметные области предиката, x 1, …, xn – предметные переменные предиката.

Предикатные формулы n Так как при подстановке различных значений вместо переменных предикат может принимать значения 0 или 1, то выражение P(x 1, …, xn) является переменным высказыванием n !!! P(x 1, …, xn) — это логическая переменная, а x 1, …, xn — нелогические переменные. n Поскольку предикаты принимают два значения и интерпретируются как высказывания, из них можно образовывать выражения логики высказываний, т. е. формулы вида n От скольких предметных переменных зависит данный предикат? n От скольких логических переменных зависит данное высказывание?

Примеры предикатов n Предикат тождества E(x 1, x 2): N 2 B: E(a 1, a 2) = 1 тогда и только тогда, когда a 1 = a 2, xi N n Предикат порядка Q (x 1, x 2) : N 2 B: Q(a 1, a 2) = 1 тогда и только тогда, когда a 1 a 2, xi N n Предикат делимости D (x 1, x 2) : N 2 B: D(a 1, a 2) = 1 тогда и только тогда, когда a 1 делится на a 2, xi N n Предикат суммы S (x 1, x 2, x 3) : N 3 B: S(a 1, a 2, a 3) = 1 тогда и только тогда, когда a 1 + a 2 = a 3, xi N n Предикат произведения P (x 1, x 2, x 3) : N 3 B: P(a 1, a 2, a 3) = 1 тогда и только тогда, когда a 1 * a 2 = a 3, xi N

Задания n Упр 14. Сформулировать свойство транзитивности делимости. Составить предикатную формулы, используя предикат делимости. n Упр 15. Дать словестную формулировку предикату ((S(a, b, c)&D(a, d)&D(b, d)) D(c, d). Здесь Sпредикат суммы, D-предикат делимости

Кванторы n Пусть P(x) — предикат, определенный на M n Высказывание «для всех x из M предикат P(x) истинен» обозначается x. P(x). Знак x называется квантором общности; n Высказывание «существует такой x из M, что предикат P(x) истинен» обозначается x. P(x). Знак x называется квантором существования. n Переход от P(x) к x P(x) или x P(x) называется связыванием переменной x, а также навешиванием квантора на переменную x (или на предикат P), иногда — квантификацией переменной x. n Переменная, на которую навешен квантор, называется связанной; несвязанная переменная называется свободной.

Область действия квантора n Выражения x. P(x), x. P(x) не зависят от х и при фиксированных Р и М имеют вполне определенные значения, представляя вполне конкретное высказывание относительно всех х предметной области М. n Выражение, на которое навешивается квантор x или x называется областью действия квантора; n Все вхождения переменной x в это выражение являются связанными. n Навешивание предиката на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных.

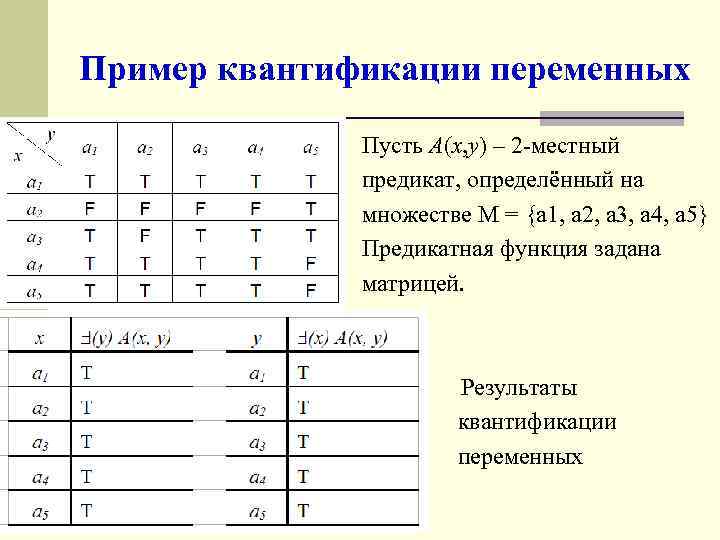
Пример квантификации переменных Пусть A(x, y) – 2 -местный предикат, определённый на множестве M = {a 1, a 2, a 3, a 4, a 5} Предикатная функция задана матрицей. n Результаты квантификации переменных

Пример квантификации переменных Пусть A(x, y) – 2 -местный предикат, определённый на множестве M = {a 1, a 2, a 3, a 4, a 5} Предикатная функция задана матрицей. n Результаты квантификации переменных

Примеры квантификации переменных n Если к оставшейся свободной переменной применить квантор, то одноместные предикаты превратятся в высказывания: n (x) (y) A(x, y)= T n (y) (x) A(x, y)= F n (x) (y) A(x, y)= n (y) (x) A(x, y)= T T

Порядок применения разноименных кванторов n Порядок применения разноимённых кванторов существенен и может привести к различным высказываниям n Определим предикат Р(x, y) = «Человек x любит у» , определенный на множестве людей. n Упр 16: x y P(x, y), y x P(x, y) 1)Сколько свободных переменных в предикатах? Сколько связанных? От скольких переменных зависят предикаты? 2)Дать словесную интерпретацию предикатов

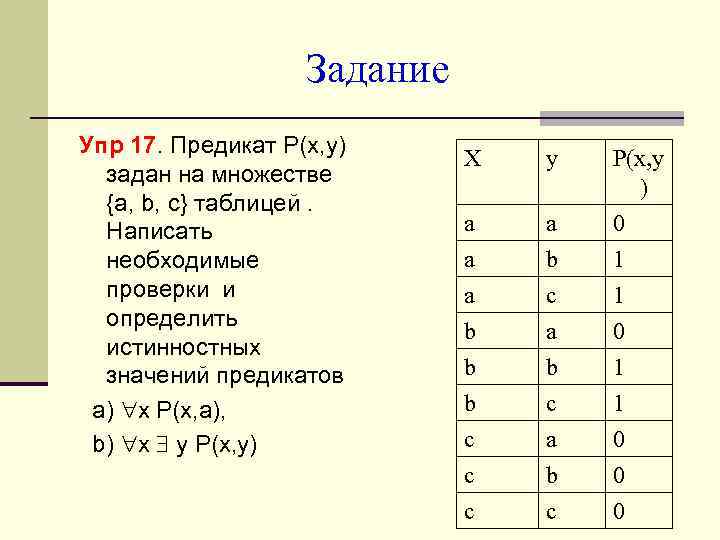Задание Упр 17. Предикат P(x, y) задан на множестве {a, b, c} таблицей. Написать необходимые проверки и определить истинностных значений предикатов a) x P(x, a), b) x y P(x, y) X y P(x, y ) a a a b 0 1 a b b b c c a b c 1 0 1 1 0 0 0

Истинностные значения формул Логики Предикатов n Если в множестве М для формулы F существует такая подстановка констант вместо всех переменных, что F становится истинным высказыванием, то формула F называется выполнимой в области М. Если существует область М, где F выполнима, то F называется просто выполнимой. n Если формула F выполнима в М при любых подстановках констант, то она называется тождественно истинной в М. Формула, тождественно истинная в любых М называется тождественно истинной или общезначимой. n Если формула F невыполнима в М, она называется тождественно ложной в М. Если F невыполнима ни в каких М, она называется тождественно ложной, или противоречивой.

Определений истинностных значений n Существуют несколько методов установления истинностных значений предикатов: 1) подстановкой 2) прямое доказательство 3) метод от противного 4) построением предикатной матрицы

Подстановка n Оценить истинностное значение предиката (x) S(x, y, x), где S(x, y, x) – предикат суммы на множествах N 0, N. n На множестве N 0 существует единственная подстановка константы вместо переменной y, такая что для любого х выражение x+y=x истинно. Очевидно, что y=0. Т. е. данный предикат выполним на множестве N 0. n Очевидно, что на множестве N такой подстановки не существует, т. е. данный предикат тождественно ложный на множестве N. n Так как существует множество на котором он выполним, то рассматриваемый предикат просто выполним.

Прямое доказательство n Пример1: Оценить истинностное значение предиката (x)(P(x)& P(x)), где P(x) – любой предикат. При подстановке любого значения а из любого множества М вместо переменной х возможны две ситуации Р(а)=1 и Р(а)=0. Рассмотрим каждую из них. Если Р(а)=1, тогда P(а)=0 и формула P(а)& P(а)=1&0=0. Если Р(а)=0, тогда P(а)=1 и формула P(а)& P(а)=0&1=0. Таким образом, предикат является тождественно ложным.

Определений истинностных значений метод от противного n Пример: Оценить истинностное значение предиката x((P(x)&Q(x))→P(x)), где P(x), Q(x) – любые предикаты. Предположим противное. Пусть формула ложна, т. е. не для всех х формула (P(x)&Q(x))→P(x) истина. Тогда существует значение а, подстановка которой в формулу делает ее ложной (P(а)&Q(а))→P(а) =0. Такая ситуация возможна если P(а)&Q(а) = 1 (1) P(а) = 0 (2) Из (1) следует, что P(а)=1, что противоречит (2) Принятое предположение относительно ложности формулы привело к противоречию, поэтому оно не верно и, следовательно, формула x((P(x)&Q(x))→P(x)) тождественно истинна

Построение предикатной матрицы n Упр 18. Определить истинностное значение предиката x S(x, y, y) на множестве M={0, 1, 2}. Где S()- предикат суммы

Эквивалентные формулы n Формулы называются эквивалентными, если при любых подстановках констант они принимают одинаковые значения. n В частности, все тождественно истинные формулы (и все ложные формулы) эквивалентны.

Тождественно Истинные формулы n Множество тождественно истинных формул логики предикатов входит в любую теорию, исследование этого множества – важная задача логики предикатов. n При этом выделяются две проблемы! 1) получение истинных формул (порождающая процедура) 2) проверка формулы на истинность (разрешающая процедура). n Для решения этих проблем используются различные косвенные приемы, в том числе эквивалентные соотношения, позволяющие выполнить корректные преобразования формул

Эквивалентные соотношения булевой алгебре n n n n n ассоциативностей a (b c)=(a b) c, a(bc)=(ab)c; коммутативностей a b=b a, ab=ba; дистрибутивностей a(b c)=(ab) (ac); a (bc)=(a b)(a c); идемпотентностей a a=a, aa=a; двойного отрицания a=a; законы 0 a 0=a, a 0=0, a a=0; законы 1 a 1=1, a 1=a, a a=1. де-Моргана a b= (a b), a b= (a b); противоречия a а=0; исключенного третьего a а=1

Эквивалентные соотношения 1) Эквивалентные соотношения алгебры предикатов включающие кванторы х, х ( x P(x)) ~ x P(x) 2) ( x P(x)) ~ x P(x) 3) x ( P 1(x) & P 2(x) ) ~ ( x P 1(x) & x P 2(x) ) дистрибутивность квантора относительно & 4) x ( P 1(x) v P 2(x) ) ~ ( x P 1(x) v x P 2(x) ) дистрибутивность квантора относительно v 5) 6) x y P(x, y) ~ y x P(x, y) коммутативность квантора 7) 8) 9) 10) x ( P(x) & & v v Y) Y) ~ ~ ( x P(x) & Y) , v Y) , где где Y не зависит от х

Префиксная нормальная форма (ПНФ) n Префиксной нормальной формой (ПНФ) называется формула, имеющая вид Q 1 x 1, Q 2 x 2, …, Qnxn. F — кванторы; F — формула, не имеющая кванторов, с операциями { , , }. n В логике предикатов для любой формулы существует эквивалентная ей префиксная нормальная форма.

Процедура получения ПНФ: 1) Заменить операции → , ~ на булевы A → B = A v B A ~ B = ( A v B) & ( A v B ) 2) При помощи эквивалентных соотношений спустить символы отрицания на предикаты 3) Если к формуле, не имеющей вид ПНФ, не применимы эквивалентные соотношения, то следует использовать правила переименования переменных 4) С помощью эквивалентных соотношений получить ПНФ

Правила переименования переменных 1) В случае не применимости эквивалентных соотношений, свободную переменную можно переименовывать. Пример: P(y) v y Q(x, y) = P(z) v y Q(x, y) 2) В случае не применимости эквивалентных соотношений, связанную переменную можно переименовывать. Примеры: а) x P(x) v x Q(x, y) = z P(z) v x Q(x, y) б) x P 1(x) v x P 2(x) = x P 1(x) v y P 2(y) в) x P 1(x) & x P 2(x) = x P 1(x) & y P 2(y)

Сколемовская форма n Сколемовская форма (СФ) – это ПНФ, в которой исключены кванторы существования. n Правила исключения квантора существования для предиката в ПНФ Q 1 x 1…Qi-1 xi Qi+1 xi+1…Qnxn F: n Пусть никакой квантор всеобщности не встречается левее xi , тогда а) выбираем новую (не встречающуюся в формуле) константу с б) в формуле F заменим все xi на с в) вычеркнем xi из префикса n Пусть есть непустой список x 1… xi-1 кванторов всеобщности, встречающихся в префиксе левее xi , тогда а) выберем новый ( не встречавшийся в формуле) функциональный символ f б) в формуле F заменим все xi на f(x 1…xi-1 ) в) вычеркнем xi из префикса n Выполнить эту процедуру для всех кванторов существования

Примеры Упр 21 Найти сколемовскую форму для ПФ : u v w x y z M(u, v, w, x, y, z). Упр 22 Найти сколемовскую форму для ПФ x y z w t ( S(x, y, y) (S(z, v, x)&P(w, t, t))),

Клаузальная форма n Клаузальной формой называется такая сколемовская форма, матрица которой является КНФ. Любая сколемовская форма допускает эквивалентную клаузальную форму. Упр 23 Найти сколемовскую форму для ПФ x y z w t( S(x, y, y) (S(z, v, x)&P(w, t, t)))

Доказательство выводимости S из системы гипотез G n Составляем предикатные формулы для n n n утверждения S и системы гипотез G. Доказательство будем проводить методом от противного, т. е. составляем формулу F=G& S Приводим F в ПНФ Приводим F в ССФ Приводим F в КФ Формуле F, представленной в виде КФ ставим в соответствие множество дизъюнктов Применяем правило резолюций. Если получена пустая резольвента, то S выводимо из G. В противном случае доказать выводимость невозможно.