 Логика и язык Тема 2
Логика и язык Тема 2
 1. ЯЗЫК КАК ЗНАКОВАЯ СИСТЕМА Язык – это система знаков, предназначенная для фиксации, хранения, переработки и передачи информации. Знак – это объект, используемый интерпретатором в процессе познания или общения в качестве представителя какого-либо другого объекта.
1. ЯЗЫК КАК ЗНАКОВАЯ СИСТЕМА Язык – это система знаков, предназначенная для фиксации, хранения, переработки и передачи информации. Знак – это объект, используемый интерпретатором в процессе познания или общения в качестве представителя какого-либо другого объекта.
 Наука о знаках – семиотика. Предметом этой науки является знаковая ситуация (семиозис) состоящая из трех элементов: семиозис Знак (это может быть произнесенное вслух или написанные слова и словосочетания, графические символы, жесты, сигналы, и т. п. ) Обозначаемое (конкретные материальные индивиды, абстрактные объекты, свойства, отношения, функции, множества, процессы, явления, события, состояния и т. п. ) Интерпретатор (это может быть отдельное лицо, группа людей или общество в целом, животные, роботы и т. п. )
Наука о знаках – семиотика. Предметом этой науки является знаковая ситуация (семиозис) состоящая из трех элементов: семиозис Знак (это может быть произнесенное вслух или написанные слова и словосочетания, графические символы, жесты, сигналы, и т. п. ) Обозначаемое (конкретные материальные индивиды, абстрактные объекты, свойства, отношения, функции, множества, процессы, явления, события, состояния и т. п. ) Интерпретатор (это может быть отдельное лицо, группа людей или общество в целом, животные, роботы и т. п. )
 Язык как знаковую систему можно рассматривать в трех аспектах: 1) Синтаксис изучает отношения между самими знаками (правила построения и преобразования выражения языка и т. д. ) 2) Семантика исследует отношения знаков к представляемым ими объектам (правила придания смысла и значения правильно построенным выражениям языка) 3) Прагматика изучает отношение интерпретатора к знакам, а также отношения между интерпретаторами в процессе языкового общения (правила и приемы практического использования знаков людьми).
Язык как знаковую систему можно рассматривать в трех аспектах: 1) Синтаксис изучает отношения между самими знаками (правила построения и преобразования выражения языка и т. д. ) 2) Семантика исследует отношения знаков к представляемым ими объектам (правила придания смысла и значения правильно построенным выражениям языка) 3) Прагматика изучает отношение интерпретатора к знакам, а также отношения между интерпретаторами в процессе языкового общения (правила и приемы практического использования знаков людьми).
 2. СМЫСЛ И ЗНАЧЕНИЕ ЗНАКА. ВИДЫ ЗНАКОВ Значение знака – это предмет, репрезентируемый данным знаком. Экстенсионал - множество всех предметов, которые знак репрезентирует. Смысл знака (интенсионал) – это информация о репрезентируемом предмете, которая позволяет интерпретатору распознать этот предмет среди остальных. Принято считать, что все знаки имеют смысл: Описательный (уже содержащийся в самом знаке) Неописательный ( придаваемый знаку как бы внешним образом, с помощью определения)
2. СМЫСЛ И ЗНАЧЕНИЕ ЗНАКА. ВИДЫ ЗНАКОВ Значение знака – это предмет, репрезентируемый данным знаком. Экстенсионал - множество всех предметов, которые знак репрезентирует. Смысл знака (интенсионал) – это информация о репрезентируемом предмете, которая позволяет интерпретатору распознать этот предмет среди остальных. Принято считать, что все знаки имеют смысл: Описательный (уже содержащийся в самом знаке) Неописательный ( придаваемый знаку как бы внешним образом, с помощью определения)
 Базисными семантическими категориями являются: Имя (n) - выражение, обозначающее какой-либо предмет или множество предметов. Предложение (s) – выражение, обозначающее истину или ложь. Все остальные семантические категории представляют собой функции, преобразующие некоторое количество выражений одной базисной категории и выражение другой базисной категории.
Базисными семантическими категориями являются: Имя (n) - выражение, обозначающее какой-либо предмет или множество предметов. Предложение (s) – выражение, обозначающее истину или ложь. Все остальные семантические категории представляют собой функции, преобразующие некоторое количество выражений одной базисной категории и выражение другой базисной категории.
 3. ЕСТЕСТВЕННЫЕ И ИСКУССТВЕННЫЕ ЯЗЫКИ Естественные языки возникли как средство общения между людьми. Их формирование и развитие представляет собой длительный исторический процесс и происходит в основном стихийно. В качестве знаков здесь используются произнесенные вслух или написанные слова и словосочетания. Искусственные языки сознательно создаются человеком для решения определенных задач. Здесь в качестве знаков используются специальные символы.
3. ЕСТЕСТВЕННЫЕ И ИСКУССТВЕННЫЕ ЯЗЫКИ Естественные языки возникли как средство общения между людьми. Их формирование и развитие представляет собой длительный исторический процесс и происходит в основном стихийно. В качестве знаков здесь используются произнесенные вслух или написанные слова и словосочетания. Искусственные языки сознательно создаются человеком для решения определенных задач. Здесь в качестве знаков используются специальные символы.
 Естественный язык обладает рядом негативных свойств: 1. Многозначность – значение некоторых выражений можно понять только из контекста. 2. Некомпозиционность – в естественном языке отсутствуют четкие правила, позволяющие определить значение сложного выражения, когда известны значения всех входящих в него слов. 3. Семантическая замкнутость – семантические атрибуты выражений естественного языка (смысл, значение, истинность и пр. ) определяются в рамках самого этого языка.
Естественный язык обладает рядом негативных свойств: 1. Многозначность – значение некоторых выражений можно понять только из контекста. 2. Некомпозиционность – в естественном языке отсутствуют четкие правила, позволяющие определить значение сложного выражения, когда известны значения всех входящих в него слов. 3. Семантическая замкнутость – семантические атрибуты выражений естественного языка (смысл, значение, истинность и пр. ) определяются в рамках самого этого языка.
 Характеристики искусственных языков Особенностью искусственных языков является то, что они позволяют фиксировать информацию о мире в максимально четкой и эффективной форме Основные характеристики искусственных знаков:
Характеристики искусственных языков Особенностью искусственных языков является то, что они позволяют фиксировать информацию о мире в максимально четкой и эффективной форме Основные характеристики искусственных знаков:
 4. СЕМАНТИЧЕСКИЕ ПРИНЦИПЫ Принцип однозначности: каждое имя должно иметь только одно значение (экстенсионал). С нарушением этого принципа связана ошибка, которую называют «подмена значения» . Принцип предметности: предложение должно говорить о предметах, обозначаемых входящими в него именами ( а не о самих этих именах). С нарушением этого принципа связана ошибка, которую называют «автономное употребление имен» .
4. СЕМАНТИЧЕСКИЕ ПРИНЦИПЫ Принцип однозначности: каждое имя должно иметь только одно значение (экстенсионал). С нарушением этого принципа связана ошибка, которую называют «подмена значения» . Принцип предметности: предложение должно говорить о предметах, обозначаемых входящими в него именами ( а не о самих этих именах). С нарушением этого принципа связана ошибка, которую называют «автономное употребление имен» .
 Принцип взаимозаменимости: при замене имен с одинаковым значением, предложение, в котором эта замена осуществляется, не должно изменять свое истинное значение (истинное предложение должно оставаться истинным, а ложное – ложным). Принцип взаимозаменяемости кажется самоочевидным, однако существует языковые контексты, в которых замена равного равным приводит к противоречию. В логике подобные ситуации известны как «антиномии отношения именования» – они возникают, когда некий объект известен субъекту в одном аспекте, и неизвестен в другом.
Принцип взаимозаменимости: при замене имен с одинаковым значением, предложение, в котором эта замена осуществляется, не должно изменять свое истинное значение (истинное предложение должно оставаться истинным, а ложное – ложным). Принцип взаимозаменяемости кажется самоочевидным, однако существует языковые контексты, в которых замена равного равным приводит к противоречию. В логике подобные ситуации известны как «антиномии отношения именования» – они возникают, когда некий объект известен субъекту в одном аспекте, и неизвестен в другом.
 5. ЯЗЫК ЛОГИКИ ВЫСКАЗЫВАНИЙ Логика высказываний (пропозициональная логика) – это раздел логики, изучающий способы построения и логическую структуру высказываний, отношения между ними и выводы, полученные с помощью логических операций конъюнкции, дизъюнкции, импликации, эквиваленции, отрицания и т. д. Алфавит логики высказываний включает в себя четыре вида символов: 1) 2) 3) 4) Пропозициональные переменные – p, q, r, s, . . . Пропозициональные связи - , &, , Скобки - ( … ) Запятая - ,
5. ЯЗЫК ЛОГИКИ ВЫСКАЗЫВАНИЙ Логика высказываний (пропозициональная логика) – это раздел логики, изучающий способы построения и логическую структуру высказываний, отношения между ними и выводы, полученные с помощью логических операций конъюнкции, дизъюнкции, импликации, эквиваленции, отрицания и т. д. Алфавит логики высказываний включает в себя четыре вида символов: 1) 2) 3) 4) Пропозициональные переменные – p, q, r, s, . . . Пропозициональные связи - , &, , Скобки - ( … ) Запятая - ,
 Пропозициональные переменные замещают собой простые высказывания. Пропозициональные связки предназначены для того, чтобы объединять простые высказывания в более сложные. К ним относятся: – ОТРИЦАНИЕ ( «НЕ» ; «НЕВЕРНО, ЧТО» , «НЕПРАВДА, ЧТО» И Т. П. ) & – КОНЪЮНКЦИЯ ( «И» , «А» , «НО» , «ХОТЯ» , И Т. П. ) – ДИЗЪЮНКЦИЯ ( «ИЛИ» , «ПО КРАЙНЕЙ МЕРЕ ОДНО ИЗ ДВУХ» И Т. П. ) – СТРОГАЯ ДИЗЪЮНКЦИЯ ( «ЛИБО-ЛИБО» , «ТОЛЬКО ОДНО ИЗ ДВУХ» И Т. П. ) – ИМПЛИКАЦИЯ ( «ЕСЛИ, ТО» , «ЗНАЧИТ» , «ВЫТЕКАЕТ» И Т. П. ) – ЭКВИВАЛЕНЦИЯ ( «ЕСЛИ И ТОЛЬКО ЕСЛИ» , «РАВНОЗНАЧНО»
Пропозициональные переменные замещают собой простые высказывания. Пропозициональные связки предназначены для того, чтобы объединять простые высказывания в более сложные. К ним относятся: – ОТРИЦАНИЕ ( «НЕ» ; «НЕВЕРНО, ЧТО» , «НЕПРАВДА, ЧТО» И Т. П. ) & – КОНЪЮНКЦИЯ ( «И» , «А» , «НО» , «ХОТЯ» , И Т. П. ) – ДИЗЪЮНКЦИЯ ( «ИЛИ» , «ПО КРАЙНЕЙ МЕРЕ ОДНО ИЗ ДВУХ» И Т. П. ) – СТРОГАЯ ДИЗЪЮНКЦИЯ ( «ЛИБО-ЛИБО» , «ТОЛЬКО ОДНО ИЗ ДВУХ» И Т. П. ) – ИМПЛИКАЦИЯ ( «ЕСЛИ, ТО» , «ЗНАЧИТ» , «ВЫТЕКАЕТ» И Т. П. ) – ЭКВИВАЛЕНЦИЯ ( «ЕСЛИ И ТОЛЬКО ЕСЛИ» , «РАВНОЗНАЧНО»
 Семантика языка КЛВ основана на двух принципах: Принцип бивалентности. Каждая пропозициональная переменная, замещающая собой простое предложение, может быть либо истинной (1), либо ложной (0). Принцип композициональности. Истинностное значение сложной формулы есть функция от истинностных значений входящих в нее переменных. Каждая пропозициональная связка трактуется как истинностно-истинностная функция.
Семантика языка КЛВ основана на двух принципах: Принцип бивалентности. Каждая пропозициональная переменная, замещающая собой простое предложение, может быть либо истинной (1), либо ложной (0). Принцип композициональности. Истинностное значение сложной формулы есть функция от истинностных значений входящих в нее переменных. Каждая пропозициональная связка трактуется как истинностно-истинностная функция.
 Алгоритм построения таблицы истинности 1. Определить число переменных 2. Определить число строк в таблице истинности 3. Записать все возможные значения переменных 4. Определить количество логических операций и их порядок 5. Записать логические операции в таблицу истинности и определить для каждой значение
Алгоритм построения таблицы истинности 1. Определить число переменных 2. Определить число строк в таблице истинности 3. Записать все возможные значения переменных 4. Определить количество логических операций и их порядок 5. Записать логические операции в таблицу истинности и определить для каждой значение
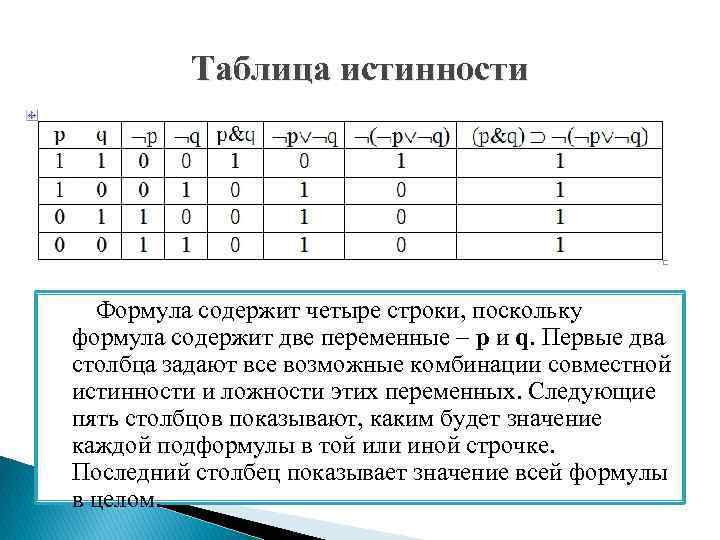 Таблица истинности Формула содержит четыре строки, поскольку формула содержит две переменные – p и q. Первые два столбца задают все возможные комбинации совместной истинности и ложности этих переменных. Следующие пять столбцов показывают, каким будет значение каждой подформулы в той или иной строчке. Последний столбец показывает значение всей формулы в целом.
Таблица истинности Формула содержит четыре строки, поскольку формула содержит две переменные – p и q. Первые два столбца задают все возможные комбинации совместной истинности и ложности этих переменных. Следующие пять столбцов показывают, каким будет значение каждой подформулы в той или иной строчке. Последний столбец показывает значение всей формулы в целом.
 В зависимости от того, каким является результирующий столбец таблицы, выделяют три вида формул: Тождественно-истинные (общезначимые) – формулы, принимающие значение « 1» во всех строках таблицы. Тождественно-ложные (невыполнимые) – формулы, принимающие значение « 0» во всех строках таблицы. Логически случайные (особенно выполнимые) – формулы, принимающие в некоторых строках таблицы значение « 1» , а в некоторый – « 0» .
В зависимости от того, каким является результирующий столбец таблицы, выделяют три вида формул: Тождественно-истинные (общезначимые) – формулы, принимающие значение « 1» во всех строках таблицы. Тождественно-ложные (невыполнимые) – формулы, принимающие значение « 0» во всех строках таблицы. Логически случайные (особенно выполнимые) – формулы, принимающие в некоторых строках таблицы значение « 1» , а в некоторый – « 0» .
 6. ОСНОВНЫЕ ЗАКОНЫ ЛОГИКИ Законом логики называется сложное логическое высказывание, истинность которого не зависит от составляющих его логических отношений. Они составляют основу мыслительного процесса и обусловливают правильность рассуждений. Правильно размышлять означает рассуждать в соответствии с законами логики.
6. ОСНОВНЫЕ ЗАКОНЫ ЛОГИКИ Законом логики называется сложное логическое высказывание, истинность которого не зависит от составляющих его логических отношений. Они составляют основу мыслительного процесса и обусловливают правильность рассуждений. Правильно размышлять означает рассуждать в соответствии с законами логики.
 Наиболее часто в практике рассуждений используются следующие законы логики: 1) Закон тождества А А Если высказывание истинно, то оно истинно. Например, «Все профессора есть профессора» . 2) Закон непротиворечия (А А) Два противоречащих другу высказывания не могут быть одновременно истинными. Например, “Это яблоко спелое” и “Это яблоко не спелое”. 3) Закон исключенного третьего А А Из двух противоречащих другу высказываний по крайней мере одно истинно. Например, “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание.
Наиболее часто в практике рассуждений используются следующие законы логики: 1) Закон тождества А А Если высказывание истинно, то оно истинно. Например, «Все профессора есть профессора» . 2) Закон непротиворечия (А А) Два противоречащих другу высказывания не могут быть одновременно истинными. Например, “Это яблоко спелое” и “Это яблоко не спелое”. 3) Закон исключенного третьего А А Из двух противоречащих другу высказываний по крайней мере одно истинно. Например, “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание.
 4) Закон двойного отрицания А А Двойное отрицание высказывания равнозначно его утверждению. Например, «Он не может не знать логику» . Значит – он знает логику. 5) Закон достаточного основания А есть потому, что есть В Всякая мысль может быть признана истинной только тогда, когда она имеет достаточное основание. Например, «Это вещество является электропроводным, потому что оно – металл» . 6) Закон утверждения консеквента А (В А) Заведомо истинное высказывание вытекает из чего угодно. Например, «Солнце всходит на востоке, а заходит на западе – так говорила мне бабушка» .
4) Закон двойного отрицания А А Двойное отрицание высказывания равнозначно его утверждению. Например, «Он не может не знать логику» . Значит – он знает логику. 5) Закон достаточного основания А есть потому, что есть В Всякая мысль может быть признана истинной только тогда, когда она имеет достаточное основание. Например, «Это вещество является электропроводным, потому что оно – металл» . 6) Закон утверждения консеквента А (В А) Заведомо истинное высказывание вытекает из чего угодно. Например, «Солнце всходит на востоке, а заходит на западе – так говорила мне бабушка» .
 7) Закон отрицания антецедента (или Закон Дунса Скота) А (А В) Из заведомо ложного высказывания вытекает что угодно. Например, «Если он миллиардер, тогда я арабский шейх» . 8) Законы Де Моргана (А В) А В Отрицание конъюнкции равнозначно дизъюнкции двух отрицаний. Например, «Неверно, что сегодня не холодно и не сыро» означает «Сегодня холодно или сыро» . (А В) А В Отрицание дизъюнкции равнозначно конъюнкции двух отрицаний. Например, «Неверно, что идет дождь или идет снег» означает «Сегодня нет дождя и нет снега» .
7) Закон отрицания антецедента (или Закон Дунса Скота) А (А В) Из заведомо ложного высказывания вытекает что угодно. Например, «Если он миллиардер, тогда я арабский шейх» . 8) Законы Де Моргана (А В) А В Отрицание конъюнкции равнозначно дизъюнкции двух отрицаний. Например, «Неверно, что сегодня не холодно и не сыро» означает «Сегодня холодно или сыро» . (А В) А В Отрицание дизъюнкции равнозначно конъюнкции двух отрицаний. Например, «Неверно, что идет дождь или идет снег» означает «Сегодня нет дождя и нет снега» .
 9) Закон контрапозиции (A В) ( В А) Если из одного высказывания вытекает второе, то из отрицания второго вытекает отрицание первого. Например, «Если вода замерзла, то на улице – морозно» и «Если на улице не морозно, то и вода не замерзла» . 10) Закон транзитивности импликации ((A В) (В С)) (А С) Если из одного высказывания вытекает второе, а из него – третье, то и из первого высказывания вытекает третье. Например, «С наступлением весны днем становится солнечнее и теплей. Когда днем становится солнечнее и теплей тает снег. Следовательно, можно сказать, что с наступлением весны тает снег» .
9) Закон контрапозиции (A В) ( В А) Если из одного высказывания вытекает второе, то из отрицания второго вытекает отрицание первого. Например, «Если вода замерзла, то на улице – морозно» и «Если на улице не морозно, то и вода не замерзла» . 10) Закон транзитивности импликации ((A В) (В С)) (А С) Если из одного высказывания вытекает второе, а из него – третье, то и из первого высказывания вытекает третье. Например, «С наступлением весны днем становится солнечнее и теплей. Когда днем становится солнечнее и теплей тает снег. Следовательно, можно сказать, что с наступлением весны тает снег» .
 11) Законы дистрибутивности дизъюнкции относительно конъюнкции и наоборот А (В С) (А В) (А C) А & (В С) (А & В) (А & C) Они позволяют пронести дизъюнкцию внутрь конъюнктивной формулы, а конъюнкцию – внутрь дизъюнктивной формулы, т. е. одну логическую связь относительно другой. Пример: распределение дизъюнкции относительно конъюнкции: «Завтра тепло или послезавтра будет холодно и дождь, тогда и только тогда, когда завтра будет тепло или послезавтра будет холодно и завтра будет тепло или послезавтра будет дождь» . При распределении конъюнкции относительно дизъюнкции: «Сегодня идет дождь и завтра тепло и послезавтра тепло в том и только в том случае, когда сегодня идет дождь и завтра тепло или сегодня идет дождь и послезавтра тепло» .
11) Законы дистрибутивности дизъюнкции относительно конъюнкции и наоборот А (В С) (А В) (А C) А & (В С) (А & В) (А & C) Они позволяют пронести дизъюнкцию внутрь конъюнктивной формулы, а конъюнкцию – внутрь дизъюнктивной формулы, т. е. одну логическую связь относительно другой. Пример: распределение дизъюнкции относительно конъюнкции: «Завтра тепло или послезавтра будет холодно и дождь, тогда и только тогда, когда завтра будет тепло или послезавтра будет холодно и завтра будет тепло или послезавтра будет дождь» . При распределении конъюнкции относительно дизъюнкции: «Сегодня идет дождь и завтра тепло и послезавтра тепло в том и только в том случае, когда сегодня идет дождь и завтра тепло или сегодня идет дождь и послезавтра тепло» .
 12) Закон Клавия ( А A) A Если из отрицания некоторого высказывания вытекает само это высказывание, то оно является истинным. Пример: необходимо доказать утверждение «Квадрат – это правильный четырехугольник, у которого все углы прямые» . Отрицание этого утверждения: «Неверно, что квадрат – это правильный четырехугольник, у которого все углы прямые» . Если из этого отрицания следует само утверждение, то это будет означать, что оно истинно.
12) Закон Клавия ( А A) A Если из отрицания некоторого высказывания вытекает само это высказывание, то оно является истинным. Пример: необходимо доказать утверждение «Квадрат – это правильный четырехугольник, у которого все углы прямые» . Отрицание этого утверждения: «Неверно, что квадрат – это правильный четырехугольник, у которого все углы прямые» . Если из этого отрицания следует само утверждение, то это будет означать, что оно истинно.
 7. Логико-семантические парадоксы В языке встречаются неустранимые противоречия, называемые парадоксами или антиномиями.
7. Логико-семантические парадоксы В языке встречаются неустранимые противоречия, называемые парадоксами или антиномиями.
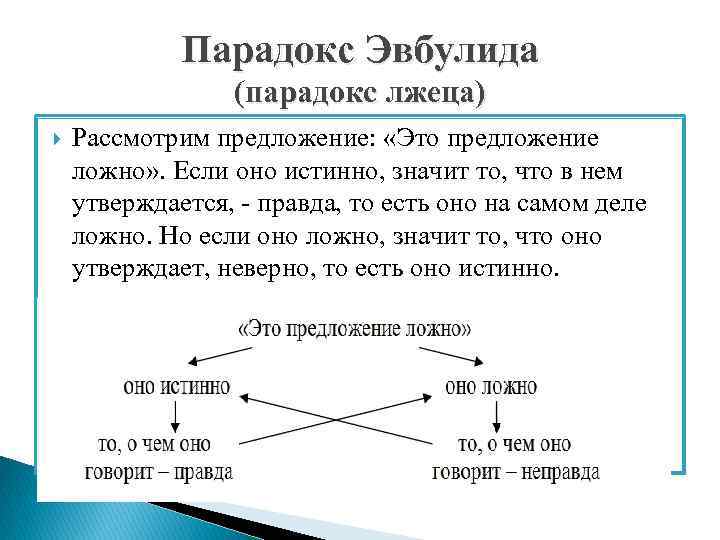 Парадокс Эвбулида (парадокс лжеца) Рассмотрим предложение: «Это предложение ложно» . Если оно истинно, значит то, что в нем утверждается, - правда, то есть оно на самом деле ложно. Но если оно ложно, значит то, что оно утверждает, неверно, то есть оно истинно.
Парадокс Эвбулида (парадокс лжеца) Рассмотрим предложение: «Это предложение ложно» . Если оно истинно, значит то, что в нем утверждается, - правда, то есть оно на самом деле ложно. Но если оно ложно, значит то, что оно утверждает, неверно, то есть оно истинно.
 Парадокс Греллинга-Нельсона (парадокс гетерологичности) Пусть все прилагательные деляться на две категории: Автологические – обладающие свойством, про которое говорят; (Слово «понятный» само является понятным, слово «русский» само является русским. ) Гетерологические – не обладающие свойством, про которое говорят. (Слово «усатый» само не носит усов, слово «длинный» само не является длинным).
Парадокс Греллинга-Нельсона (парадокс гетерологичности) Пусть все прилагательные деляться на две категории: Автологические – обладающие свойством, про которое говорят; (Слово «понятный» само является понятным, слово «русский» само является русским. ) Гетерологические – не обладающие свойством, про которое говорят. (Слово «усатый» само не носит усов, слово «длинный» само не является длинным).
 Парадокс Греллинга-Нельсона (парадокс гетерологичности) К какому типу относится прилагательное «гетерологический» ? Если оно автологическое, то должно обладать свойством, про которое говорит, то есть быть гетерологическим. Но если это слово гетерологическое, то оно не должно обадать свойством, про которое говорит, то есть должно быть автологическим.
Парадокс Греллинга-Нельсона (парадокс гетерологичности) К какому типу относится прилагательное «гетерологический» ? Если оно автологическое, то должно обладать свойством, про которое говорит, то есть быть гетерологическим. Но если это слово гетерологическое, то оно не должно обадать свойством, про которое говорит, то есть должно быть автологическим.
 Парадокс Ришара-Берри (парадокс определимости) В русском языке числа можно выражать с помощью слов и словосочетаний. Пусть k – минимальное число, которое нельзя выразить словосочетанием, состоящим менее чем из ста букв. Но сама фраза, выделенная курсивом, состоит менее чем из ста букв (точнее – из 78). И все-таки, она вполне однозначно определяет число k. Значит, число k можно выразить словосочетанием, состоящим менее чем из ста букв
Парадокс Ришара-Берри (парадокс определимости) В русском языке числа можно выражать с помощью слов и словосочетаний. Пусть k – минимальное число, которое нельзя выразить словосочетанием, состоящим менее чем из ста букв. Но сама фраза, выделенная курсивом, состоит менее чем из ста букв (точнее – из 78). И все-таки, она вполне однозначно определяет число k. Значит, число k можно выразить словосочетанием, состоящим менее чем из ста букв
 Два пути избежания логикосемантических парадоксов: 1) Семантический подход. Чтобы устранить языковые парадоксы, надо разорвать семантическую замкнутость естественного языка, то есть четко разграничить объектный язык – тот язык, который является объектом исследования, и мета-язык – тот, с помощью которого исследуется объектный язык. Тогда парадоксы исчезнут сами собой, потому что их невозможно будет сформулировать.
Два пути избежания логикосемантических парадоксов: 1) Семантический подход. Чтобы устранить языковые парадоксы, надо разорвать семантическую замкнутость естественного языка, то есть четко разграничить объектный язык – тот язык, который является объектом исследования, и мета-язык – тот, с помощью которого исследуется объектный язык. Тогда парадоксы исчезнут сами собой, потому что их невозможно будет сформулировать.
 2) Логический подход. Что бы устранить языковые парадоксы придется отказаться от классического принципа бивалентности (т. е. двузначности) для суждений. Наличие в парадоксальных рассуждениях какого-то третьего варианта устранит парадокс.
2) Логический подход. Что бы устранить языковые парадоксы придется отказаться от классического принципа бивалентности (т. е. двузначности) для суждений. Наличие в парадоксальных рассуждениях какого-то третьего варианта устранит парадокс.


