ЛОГИКА A∩B (p → q) → r

Тема I. Предмет и значение логики. • I. 1. Абстрактное мышление как ступень процесса познания. • I. 2. Язык как знаковая система. • I. 3. Логическая структура (форма) мысли. • I. 4. Законы логики и принципы правильного мышления. • I. 5. Логика как наука.
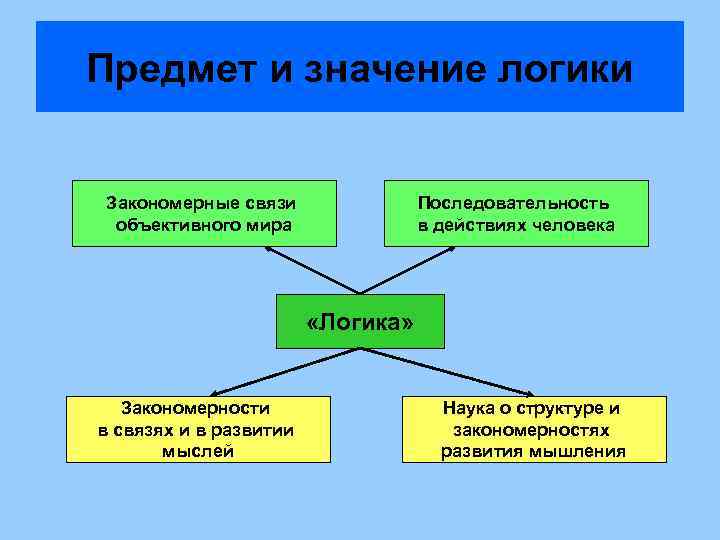
Предмет и значение логики Закономерные связи объективного мира Последовательность в действиях человека «Логика» Закономерности в связях и в развитии мыслей Наука о структуре и закономерностях развития мышления
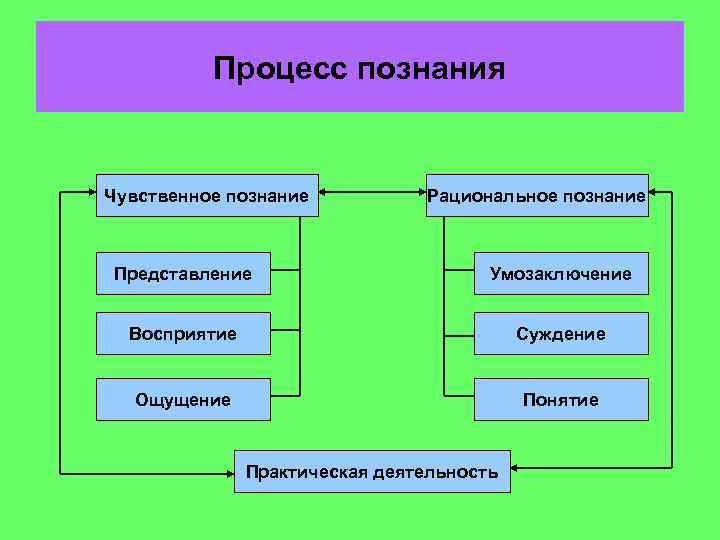
Процесс познания Чувственное познание Рациональное познание Представление Умозаключение Восприятие Суждение Ощущение Понятие Практическая деятельность
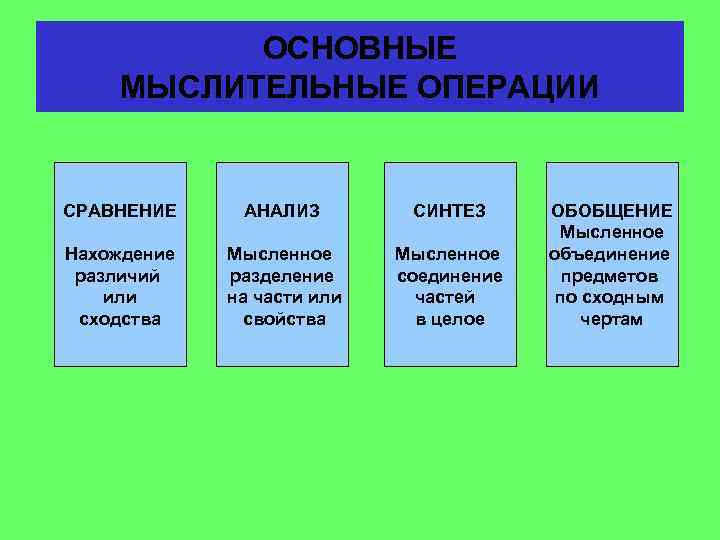
ОСНОВНЫЕ МЫСЛИТЕЛЬНЫЕ ОПЕРАЦИИ СРАВНЕНИЕ АНАЛИЗ СИНТЕЗ Нахождение различий или сходства Мысленное разделение на части или свойства Мысленное соединение частей в целое ОБОБЩЕНИЕ Мысленное объединение предметов по сходным чертам
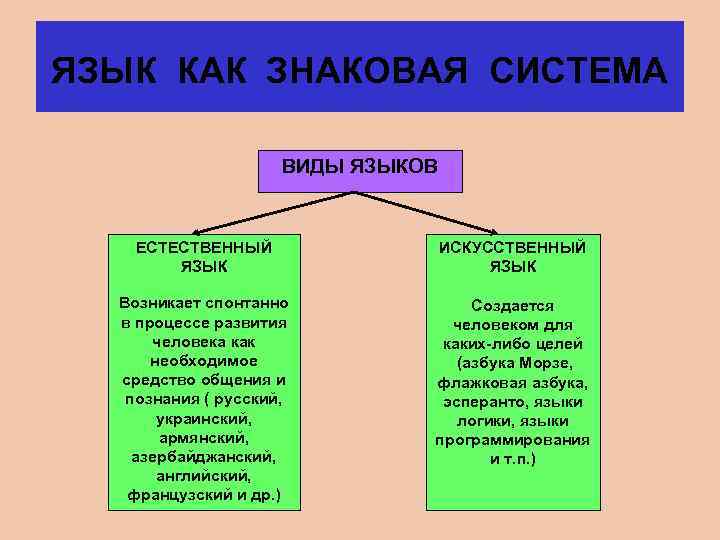
ЯЗЫК КАК ЗНАКОВАЯ СИСТЕМА ВИДЫ ЯЗЫКОВ ЕСТЕСТВЕННЫЙ ЯЗЫК ИСКУССТВЕННЫЙ ЯЗЫК Возникает спонтанно в процессе развития человека как необходимое средство общения и познания ( русский, украинский, армянский, азербайджанский, английский, французский и др. ) Создается человеком для каких-либо целей (азбука Морзе, флажковая азбука, эсперанто, языки логики, языки программирования и т. п. )
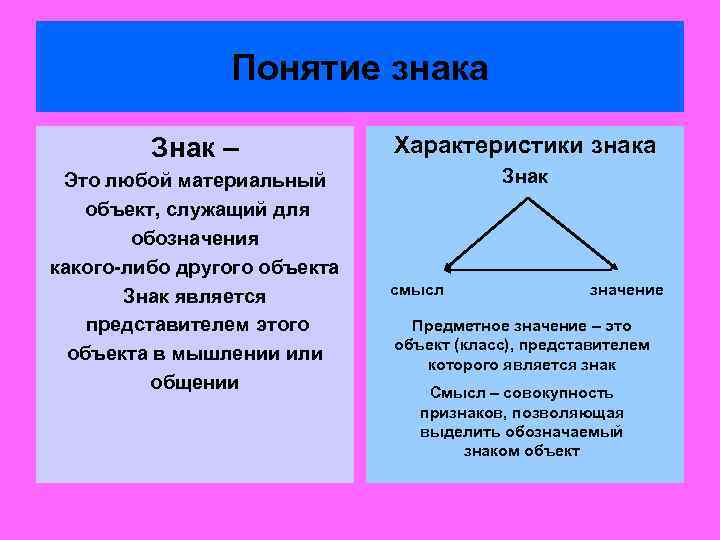
Понятие знака Знак – Характеристики знака Это любой материальный объект, служащий для обозначения какого-либо другого объекта Знак является представителем этого объекта в мышлении или общении Знак смысл значение Предметное значение – это объект (класс), представителем которого является знак Смысл – совокупность признаков, позволяющая выделить обозначаемый знаком объект
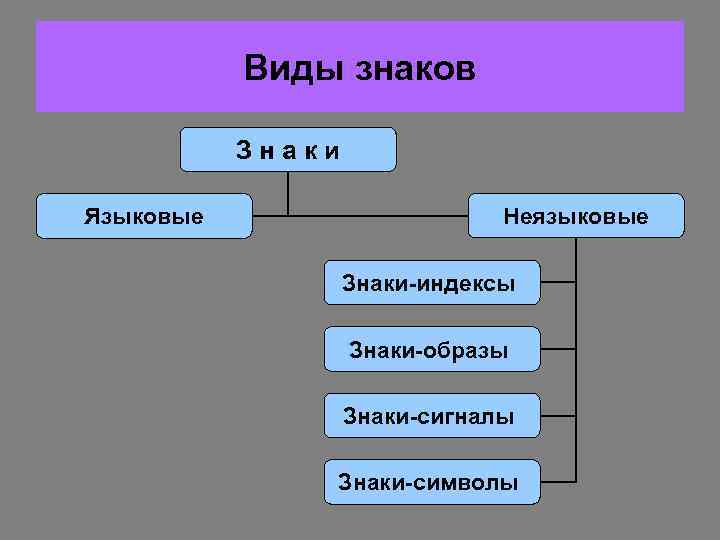
Виды знаков Знаки Языковые Неязыковые Знаки-индексы Знаки-образы Знаки-сигналы Знаки-символы

Виды знаков Знаки- индексы Знаки- образы Связаны с представляемыми ими предметами причинным образом (следы на земле, дым костра, положение стрелки спидометра) Представляют собой изображение обозначаемых предметов (иконы, картины, фотографии, схемы)

Виды знаков Знаки-символы Знаки-сигналы Никак не связаны с изображаемыми ими предметами Указывают на наступающее событие, предупреждают о чем-либо и т. п.

Уровни изучения языка Семиотика выделяет три уровня изучения языка: • С и н т а к т и к у (синтаксис) - изучает формальную структуру знаков и их сочетаний, правила их образования и преобразования • С е м а н т и к у – уделяет внимание изучению значения и смысла языковых выражений • П р а г м а т и к у – исследует отношения между знаковыми системами и теми, кто их воспринимает, интерпретирует и применяет
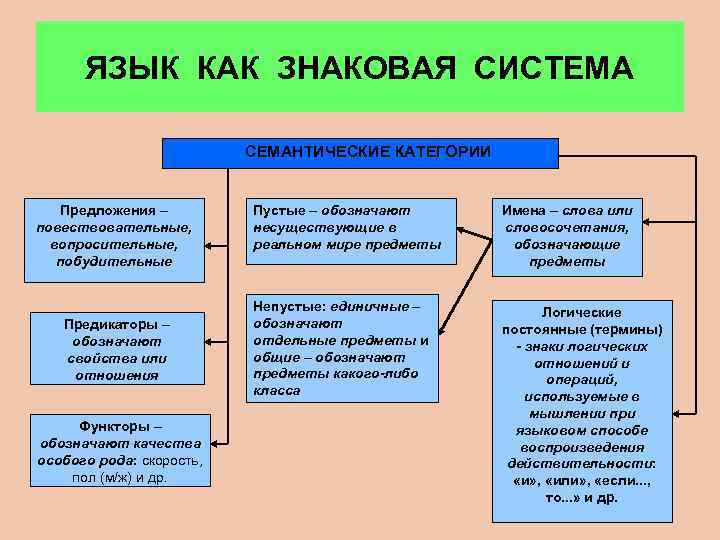
ЯЗЫК КАК ЗНАКОВАЯ СИСТЕМА СЕМАНТИЧЕСКИЕ КАТЕГОРИИ Предложения – повествовательные, вопросительные, побудительные Предикаторы – обозначают свойства или отношения Функторы – обозначают качества особого рода: скорость, пол (м/ж) и др. Пустые – обозначают несуществующие в реальном мире предметы Имена – слова или словосочетания, обозначающие предметы Непустые: единичные – обозначают отдельные предметы и общие – обозначают предметы какого-либо класса Логические постоянные (термины) - знаки логических отношений и операций, используемые в мышлении при языковом способе воспроизведения действительности: «и» , «или» , «если. . . , то. . . » и др.
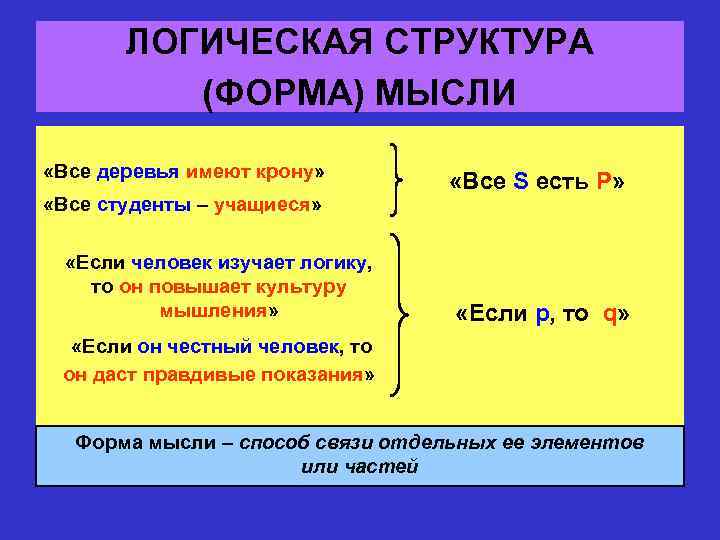
ЛОГИЧЕСКАЯ СТРУКТУРА (ФОРМА) МЫСЛИ «Все деревья имеют крону» «Все студенты – учащиеся» «Если человек изучает логику, то он повышает культуру мышления» «Все S есть P» «Если p, то q» «Если он честный человек, то он даст правдивые показания» Форма мысли – способ связи отдельных ее элементов или частей
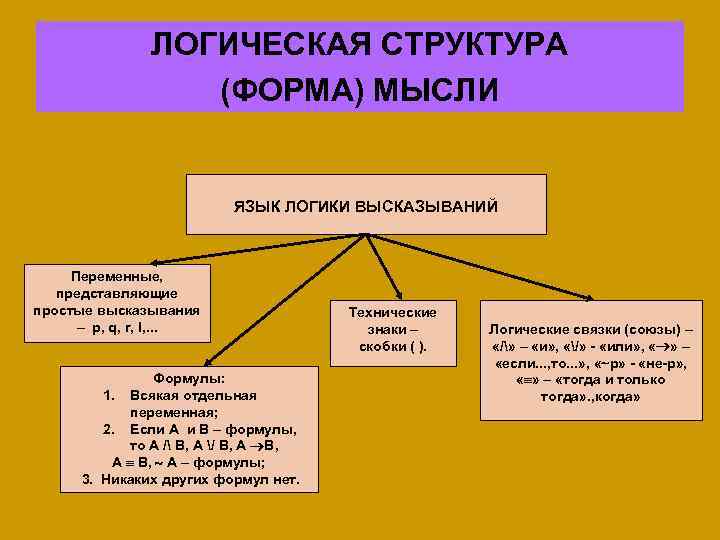
ЛОГИЧЕСКАЯ СТРУКТУРА (ФОРМА) МЫСЛИ ЯЗЫК ЛОГИКИ ВЫСКАЗЫВАНИЙ Переменные, представляющие простые высказывания – p, q, r, l, . . . Формулы: 1. Всякая отдельная переменная; 2. Если A и B – формулы, то A / B, A / B, A B, A – формулы; 3. Никаких других формул нет. Технические знаки – скобки ( ). Логические связки (союзы) – «/» – «и» , «/» - «или» , « » – «если. . . , то. . . » , «~p» - «не-p» , « » – «тогда и только тогда» . , когда»

Формализация процесс выявления структуры мысли, иначе говоря - это процесс записи с помощью символов логики некоторого выражения естественного языка Выражение «Если ты направился к цели (p), и станешь дорогою останавливаться, чтобы швырять камни во всякую лающую на тебя собаку (q), то никогда не дойдешь до цели (r)» (Ф. М. Достоевский) в языке логики высказываний имеет следующий вид: (p / q) r
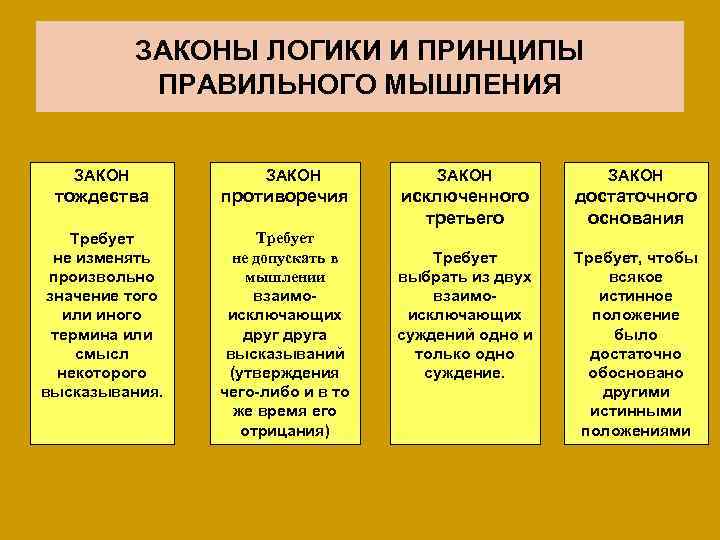
ЗАКОНЫ ЛОГИКИ И ПРИНЦИПЫ ПРАВИЛЬНОГО МЫШЛЕНИЯ ЗАКОН тождества противоречия Требует не изменять произвольно значение того или иного термина или смысл некоторого высказывания. Требует не допускать в мышлении взаимоисключающих друга высказываний (утверждения чего-либо и в то же время его отрицания) ЗАКОН исключенного третьего достаточного основания Требует выбрать из двух взаимоисключающих суждений одно и только одно суждение. Требует, чтобы всякое истинное положение было достаточно обосновано другими истинными положениями
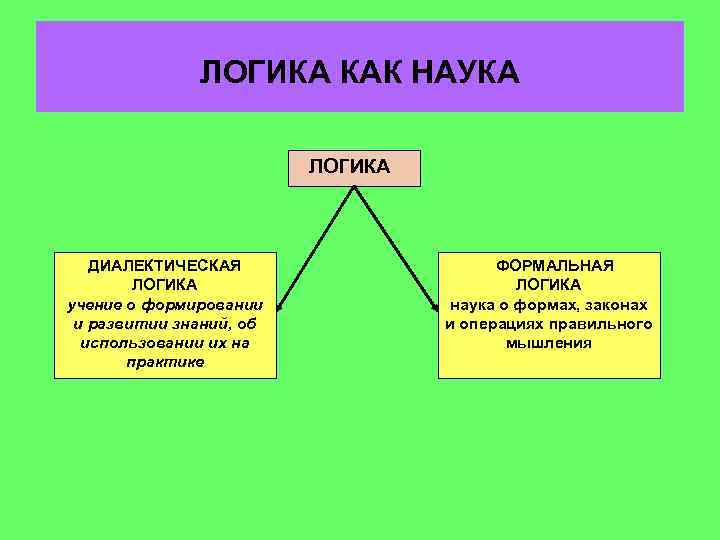
ЛОГИКА КАК НАУКА ЛОГИКА ДИАЛЕКТИЧЕСКАЯ ЛОГИКА учение о формировании и развитии знаний, об использовании их на практике ФОРМАЛЬНАЯ ЛОГИКА наука о формах, законах и операциях правильного мышления
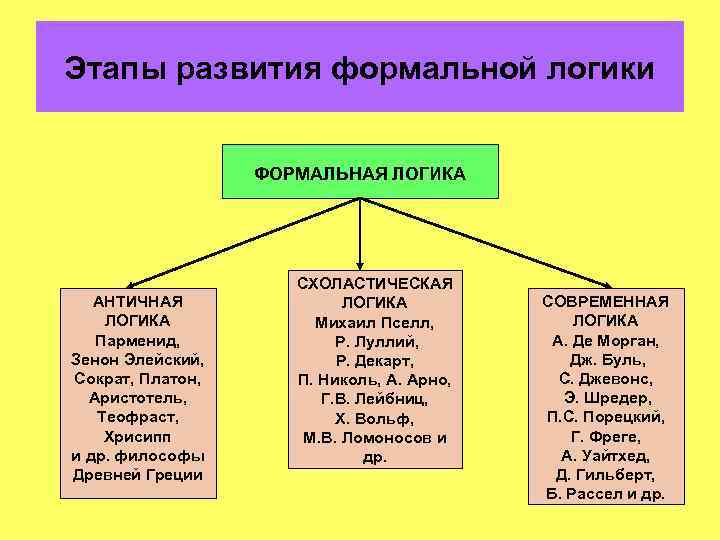
Этапы развития формальной логики ФОРМАЛЬНАЯ ЛОГИКА АНТИЧНАЯ ЛОГИКА Парменид, Зенон Элейский, Сократ, Платон, Аристотель, Теофраст, Хрисипп и др. философы Древней Греции СХОЛАСТИЧЕСКАЯ ЛОГИКА Михаил Пселл, Р. Луллий, Р. Декарт, П. Николь, А. Арно, Г. В. Лейбниц, Х. Вольф, М. В. Ломоносов и др. СОВРЕМЕННАЯ ЛОГИКА А. Де Морган, Дж. Буль, С. Джевонс, Э. Шредер, П. С. Порецкий, Г. Фреге, А. Уайтхед, Д. Гильберт, Б. Рассел и др.
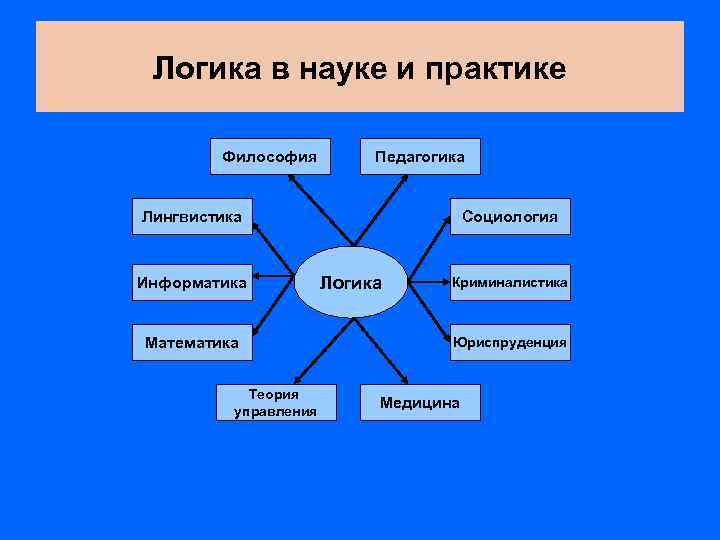
Логика в науке и практике Философия Педагогика Лингвистика Информатика Математика Теория управления Социология Логика Криминалистика Юриспруденция Медицина

Тема II. ПОНЯТИЕ II. 1. Понятие как форма мышления. II. 2. Логическая структура понятия. Закон обратного отношения между содержанием и объемом понятия. II. 3. Отношения между понятиями. II. 4. Обобщение и ограничение понятий. II. 5. Деление и классификация. II. 6. Определение понятий.

ПОНЯТИЕ КАК ФОРМА МЫШЛЕНИЯ Понятие – форма мысли, в которой на основе некоторой совокупности общих существенных признаков, свойственных предмету или группе предметов, эти предметы обобщаются и выделяются в некоторый класс • Содержание понятия – совокупность признаков, с помощью которых проведено обобщение и выделение предметов, мыслимых в данном понятии. • Объем понятия – это множество (класс) предметов, обобщенных и выделенных в данном понятии. Отдельный предмет этого множества называют элементом класса
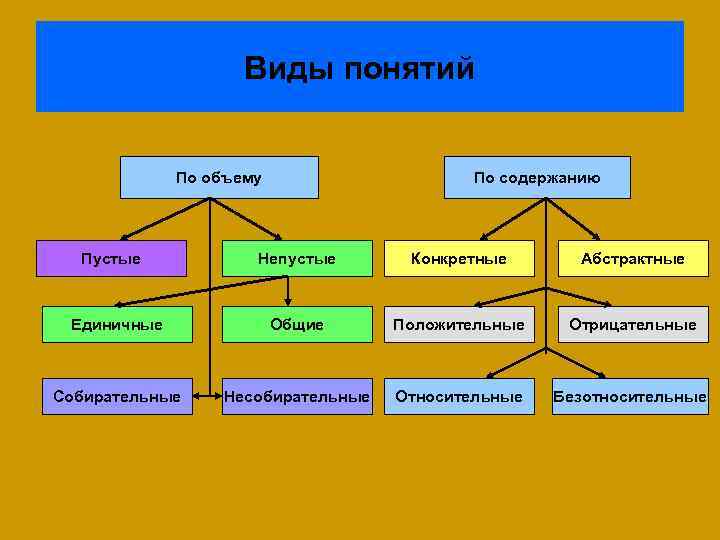
Виды понятий По объему Пустые По содержанию Непустые Конкретные Абстрактные Единичные Общие Положительные Отрицательные Собирательные Несобирательные Относительные Безотносительные
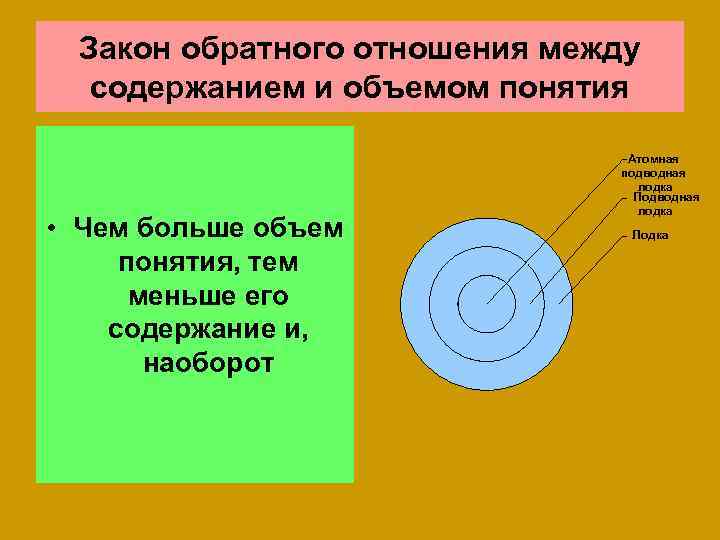
Закон обратного отношения между содержанием и объемом понятия • Чем больше объем понятия, тем меньше его содержание и, наоборот Атомная подводная лодка Подводная лодка Лодка
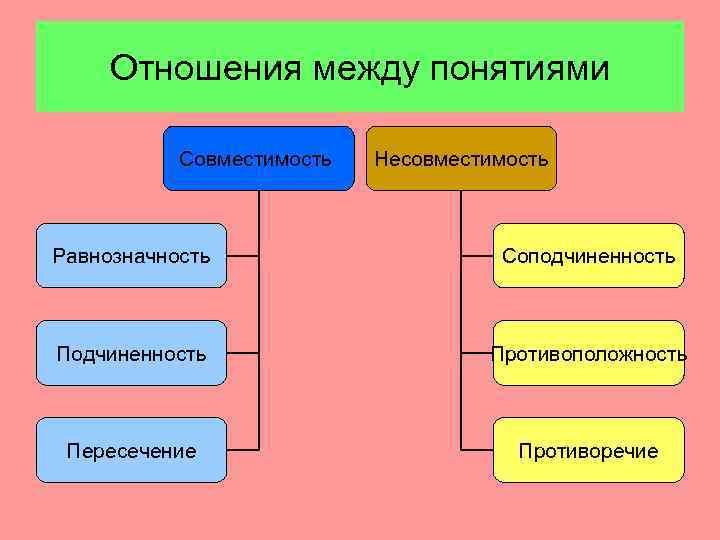
Отношения между понятиями Совместимость Несовместимость Равнозначность Соподчиненность Противоположность Пересечение Противоречие
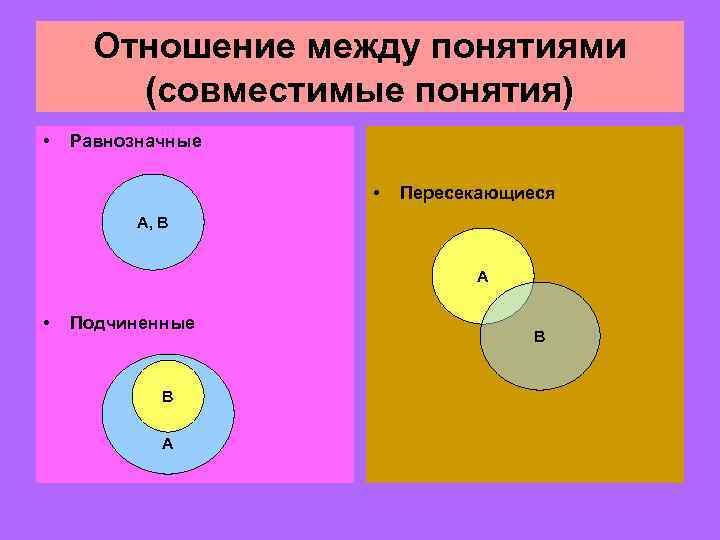
Отношение между понятиями (совместимые понятия) • Равнозначные • Пересекающиеся А, В А • Подчиненные В А В
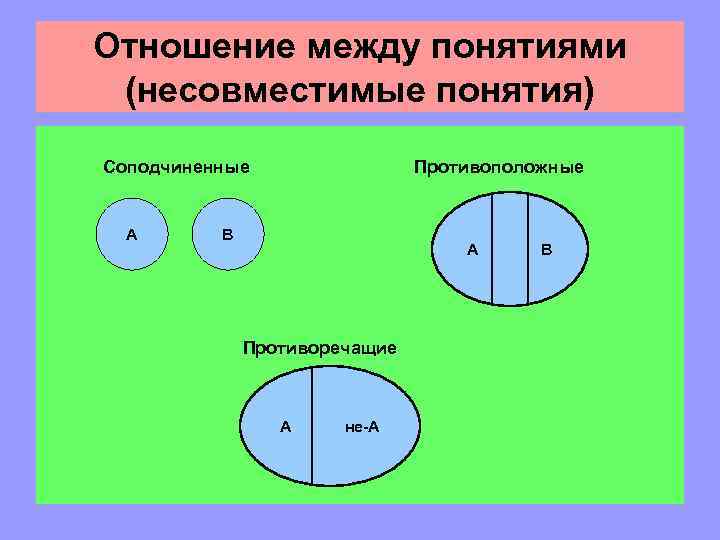
Отношение между понятиями (несовместимые понятия) Соподчиненные А Противоположные В А Противоречащие А не-А В
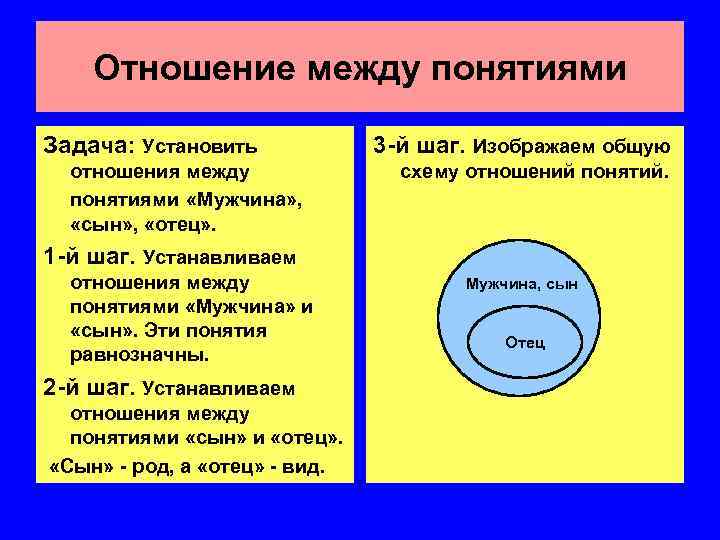
Отношение между понятиями Задача: Установить отношения между понятиями «Мужчина» , «сын» , «отец» . 3 -й шаг. Изображаем общую схему отношений понятий. 1 -й шаг. Устанавливаем отношения между понятиями «Мужчина» и «сын» . Эти понятия равнозначны. 2 -й шаг. Устанавливаем отношения между понятиями «сын» и «отец» . «Сын» - род, а «отец» - вид. Мужчина, сын Отец
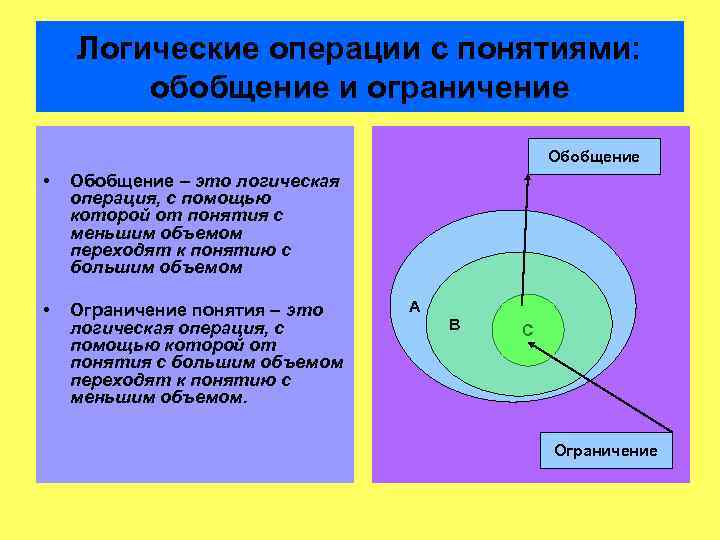
Логические операции с понятиями: обобщение и ограничение Обобщение • Обобщение – это логическая операция, с помощью которой от понятия с меньшим объемом переходят к понятию с большим объемом • Ограничение понятия – это логическая операция, с помощью которой от понятия с большим объемом переходят к понятию с меньшим объемом. А В С Ограничение
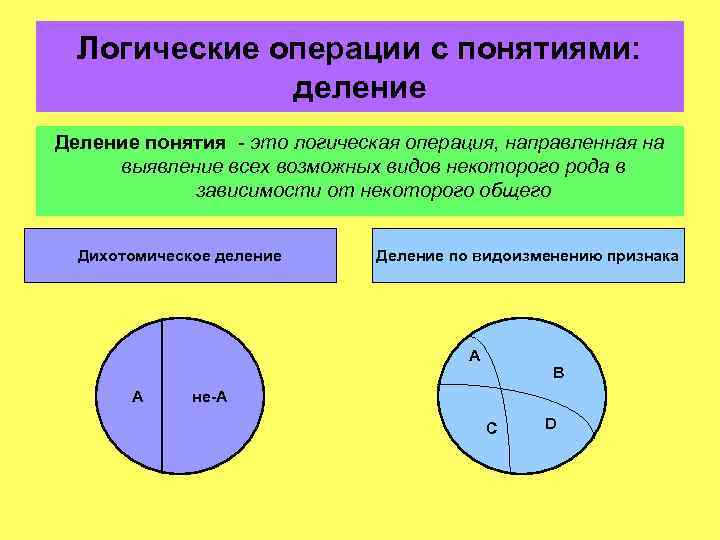
Логические операции с понятиями: деление Деление понятия - это логическая операция, направленная на выявление всех возможных видов некоторого рода в зависимости от некоторого общего Дихотомическое деление Деление по видоизменению признака А А В не-А С D

Логические операции с понятиями: деление Правила деления • Правило соразмерности: сумма (объединение) объемов членов деления должна полностью совпадать с объемом делимого понятия. • Правило исключения: члены деления должны исключать друга, т. е. быть несовместимыми понятиями. • Правило одного основания: деление должно проводиться только по одному основанию. • Правило непрерывности: в делении нельзя допускать скачков, т. е. нельзя переходить от рода к подвиду, минуя видовое понятие.
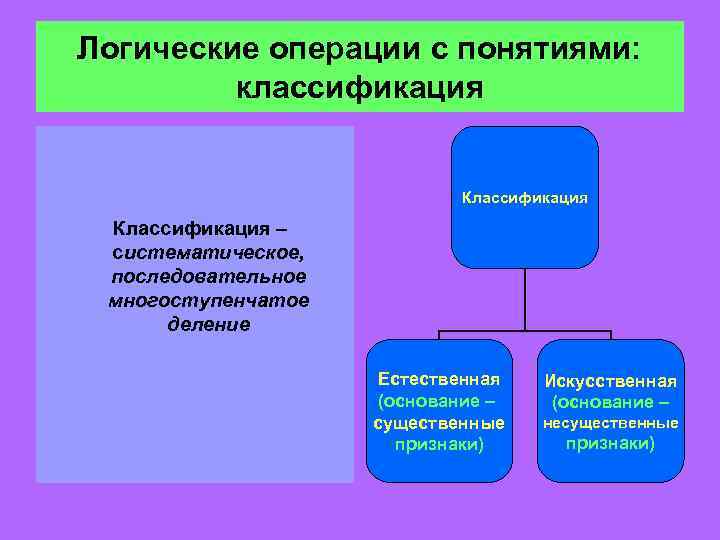
Логические операции с понятиями: классификация Классификация – систематическое, последовательное многоступенчатое деление Естественная (основание – существенные признаки) Искусственная (основание – несущественные признаки)
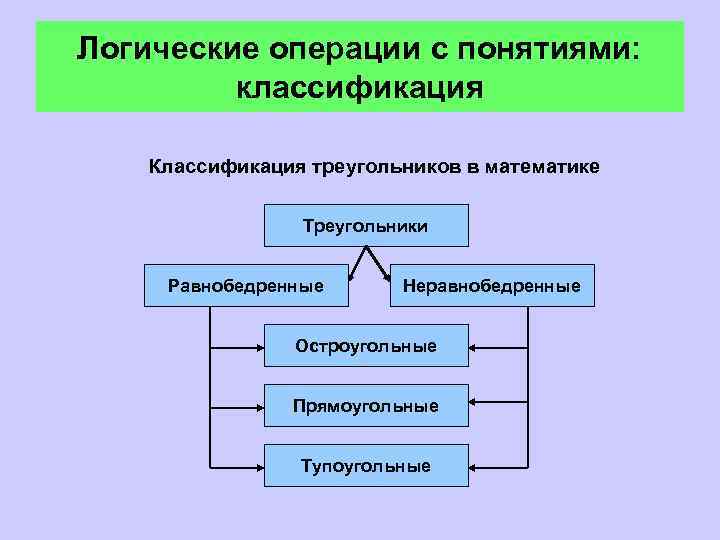
Логические операции с понятиями: классификация Классификация треугольников в математике Треугольники Равнобедренные Неравнобедренные Остроугольные Прямоугольные Тупоугольные
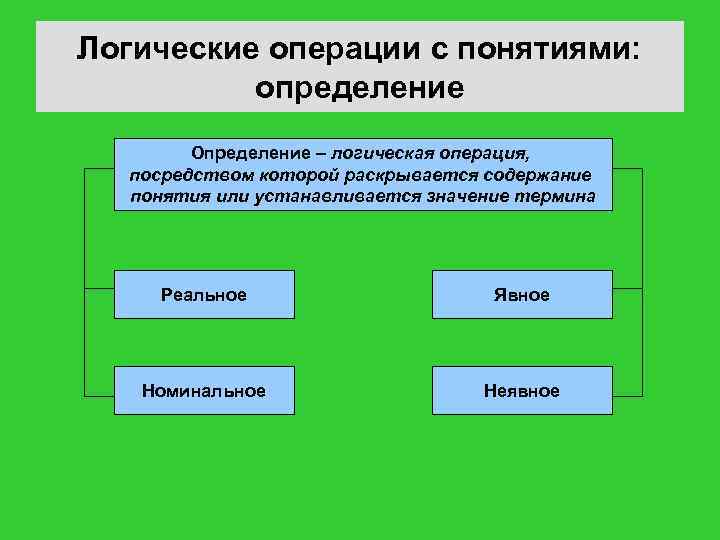
Логические операции с понятиями: определение Определение – логическая операция, посредством которой раскрывается содержание понятия или устанавливается значение термина Реальное Явное Номинальное Неявное
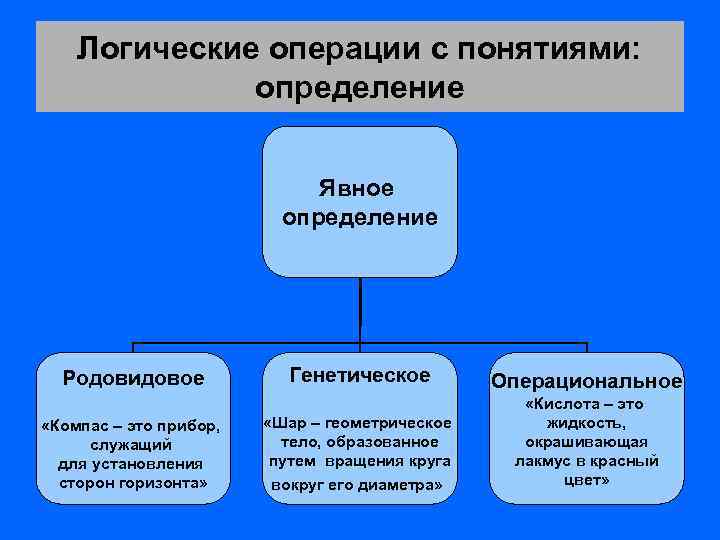
Логические операции с понятиями: определение Явное определение Родовидовое «Компас – это прибор, служащий для установления сторон горизонта» Генетическое Операциональное «Шар – геометрическое тело, образованное путем вращения круга «Кислота – это жидкость, окрашивающая лакмус в красный цвет» вокруг его диаметра»
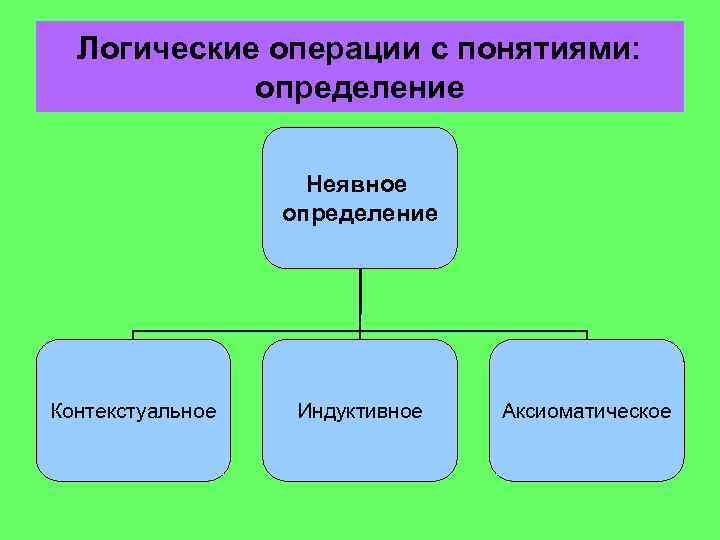
Логические операции с понятиями: определение Неявное определение Контекстуальное Индуктивное Аксиоматическое
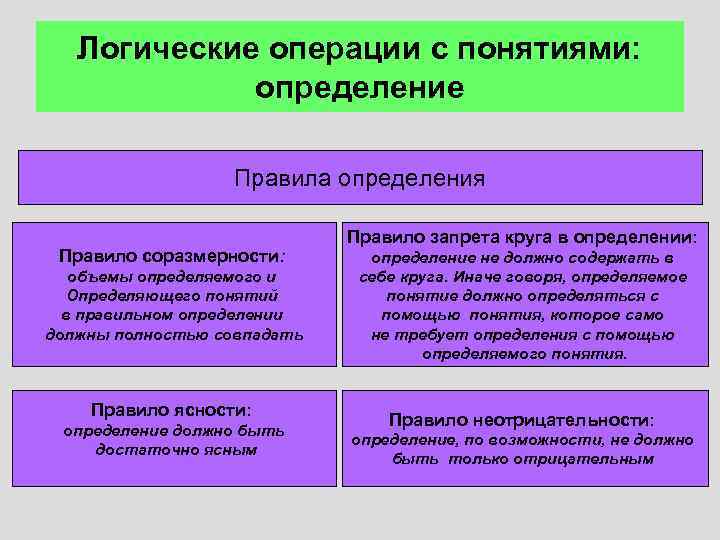
Логические операции с понятиями: определение Правила определения Правило соразмерности: объемы определяемого и Определяющего понятий в правильном определении должны полностью совпадать Правило ясности: определение должно быть достаточно ясным Правило запрета круга в определении: определение не должно содержать в себе круга. Иначе говоря, определяемое понятие должно определяться с помощью понятия, которое само не требует определения с помощью определяемого понятия. Правило неотрицательности: определение, по возможности, не должно быть только отрицательным
Логические операции с понятиями: определение Приемы, сходные с определениями Демонстрация Описание Характеристика Сравнение
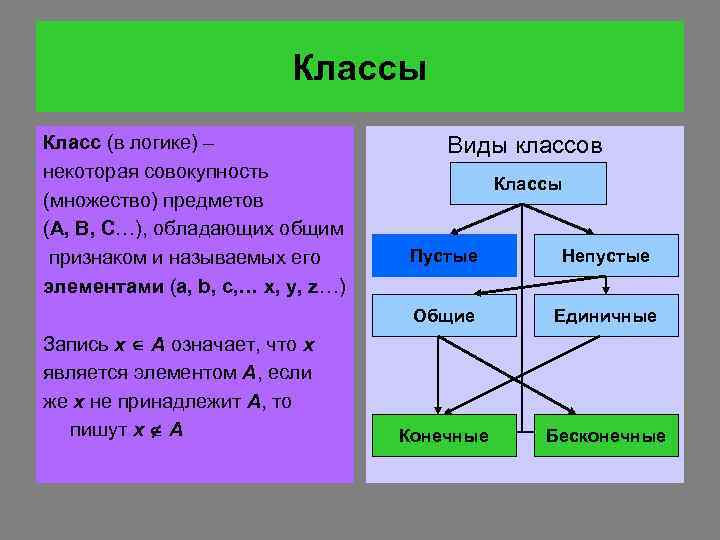
Классы Класс (в логике) – некоторая совокупность (множество) предметов (A, B, C…), обладающих общим признаком и называемых его элементами (a, b, c, … x, y, z…) Виды классов Классы Непустые Общие Запись x A означает, что x является элементом A, если же x не принадлежит А, то пишут x А Пустые Единичные Конечные Бесконечные
Классы. Операции над классами Логические операции Сложение (объединение) Умножение (пересечение) Вычитание Дополнение
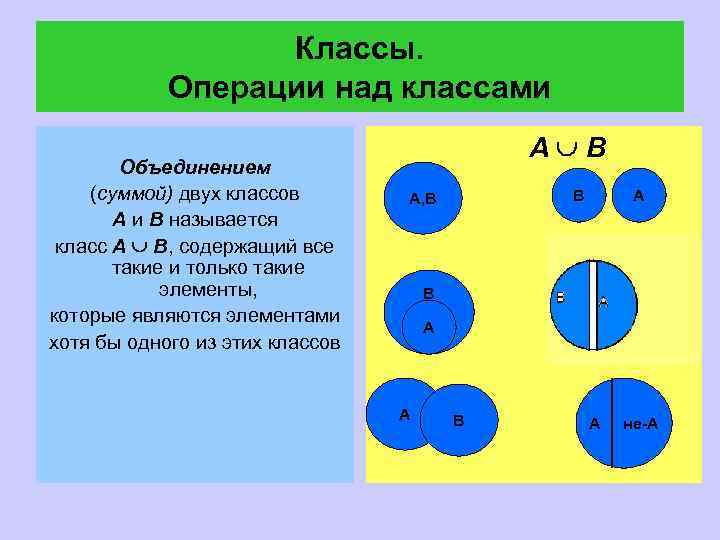
Классы. Операции над классами Объединением (суммой) двух классов A и B называется класс A B, содержащий все такие и только такие элементы, которые являются элементами хотя бы одного из этих классов A B В А, В А А В А не-А
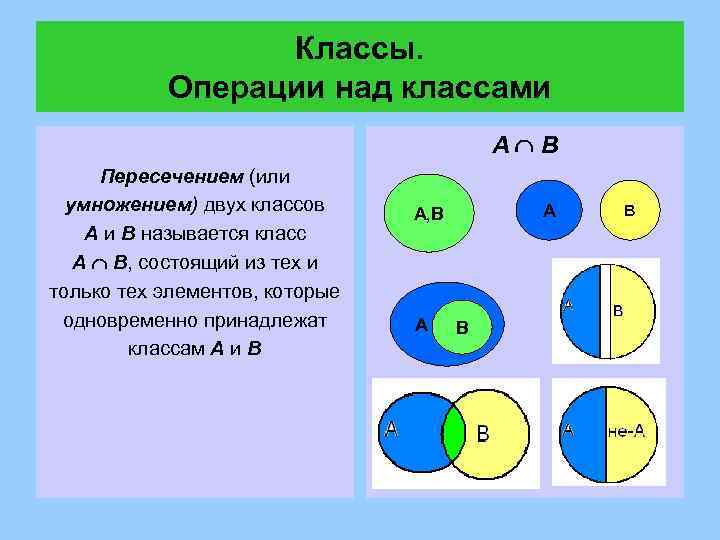
Классы. Операции над классами A B Пересечением (или умножением) двух классов A и B называется класс A B, состоящий из тех и только тех элементов, которые одновременно принадлежат классам A и В А А, В А ВВ В
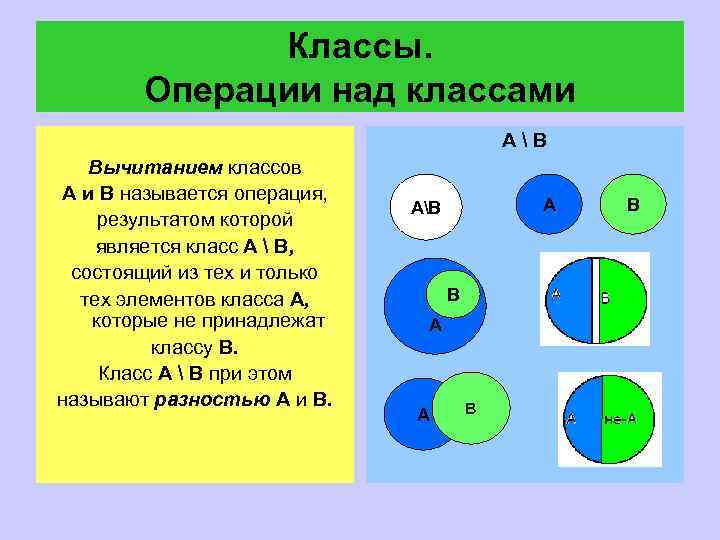
Классы. Операции над классами AB Вычитанием классов A и B называется операция, результатом которой является класс A B, состоящий из тех и только тех элементов класса A, которые не принадлежат классу В. Класс A B при этом называют разностью А и В. A АB B A A B B
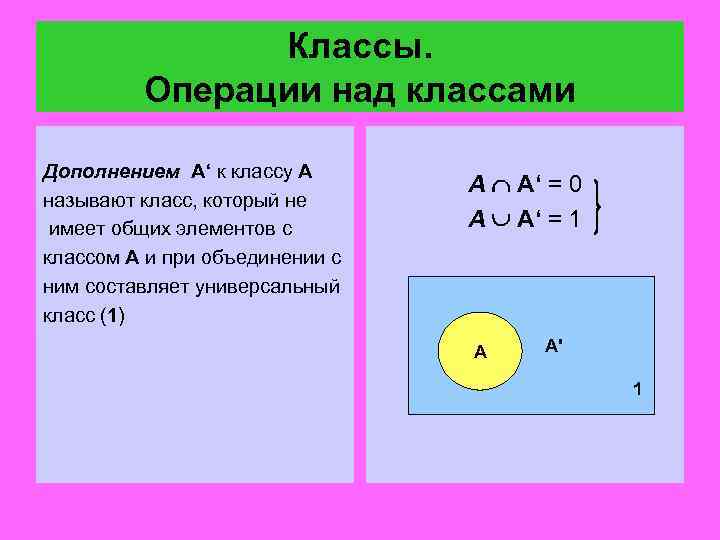
Классы. Операции над классами Дополнением А‘ к классу А называют класс, который не имеет общих элементов с классом А и при объединении с ним составляет универсальный класс (1) A А‘ = 0 A А‘ = 1 А А' 1

Тема III. Суждение. Вопрос. Норма III. 1. Суждение и его виды. III. 2. Простое категорическое суждение. III. 3. Сложное суждение. III. 4. Отношения между суждениями по их истинности. III. 5. Вопрос. III. 6. Норма.
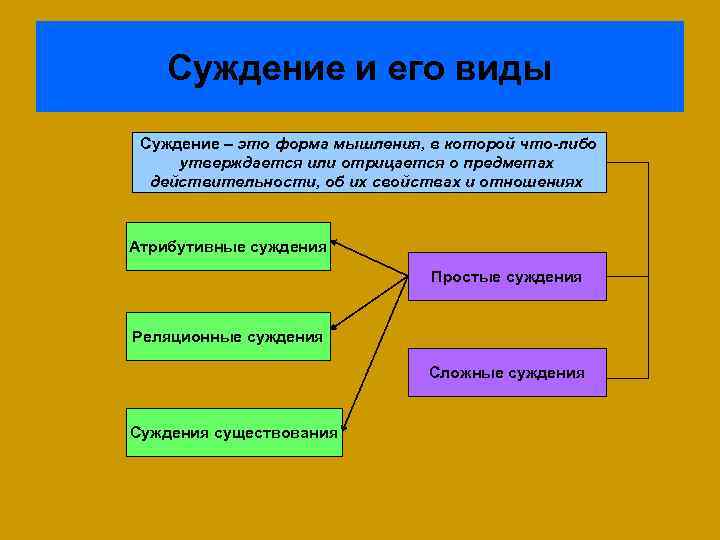
Суждение и его виды Суждение – это форма мышления, в которой что-либо утверждается или отрицается о предметах действительности, об их свойствах и отношениях Атрибутивные суждения Простые суждения Реляционные суждения Сложные суждения Суждения существования
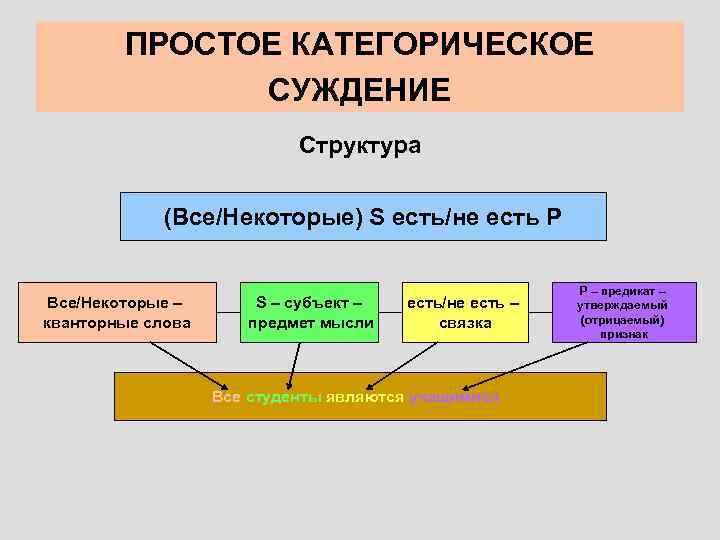
ПРОСТОЕ КАТЕГОРИЧЕСКОЕ СУЖДЕНИЕ Структура (Все/Некоторые) S есть/не есть P Все/Некоторые – кванторные слова S – субъект – предмет мысли есть/не есть – связка Все студенты являются учащимися P – предикат – утверждаемый (отрицаемый) признак
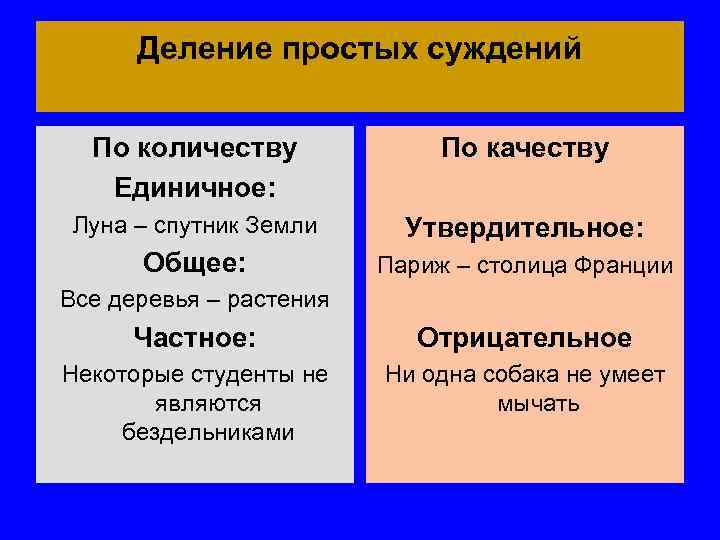
Деление простых суждений По количеству Единичное: По качеству Луна – спутник Земли Утвердительное: Общее: Париж – столица Франции Все деревья – растения Частное: Отрицательное Некоторые студенты не являются бездельниками Ни одна собака не умеет мычать
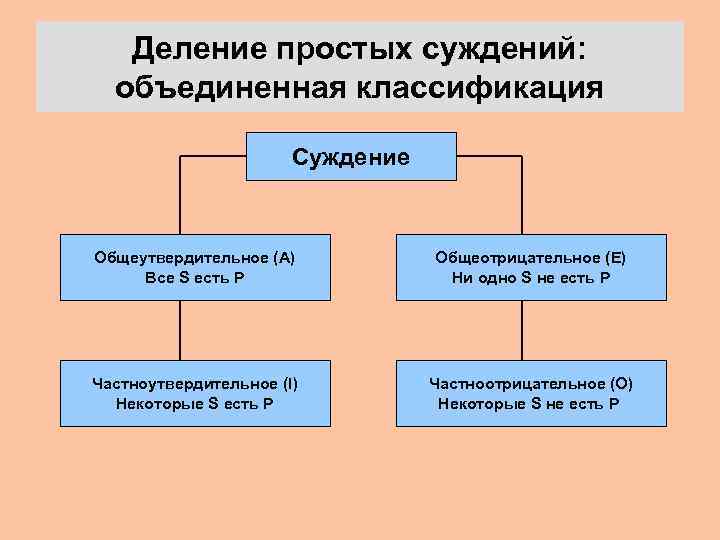
Деление простых суждений: объединенная классификация Суждение Общеутвердительное (А) Все S есть P Общеотрицательное (Е) Ни одно S не есть P Частноутвердительное (I) Некоторые S есть P Частноотрицательное (О) Некоторые S не есть P
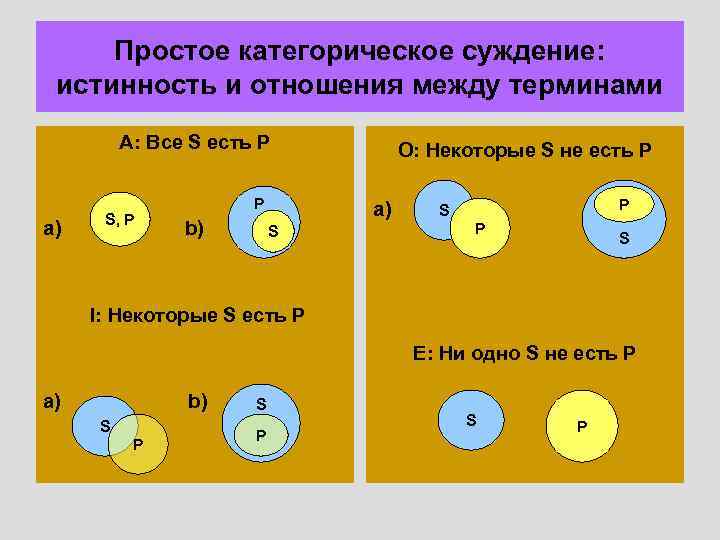
Простое категорическое суждение: истинность и отношения между терминами A: Все S есть P a) S, P P b) O: Некоторые S не есть P a) S b) S P P S I: Некоторые S есть P E: Ни одно S не есть P a) b) S P S P
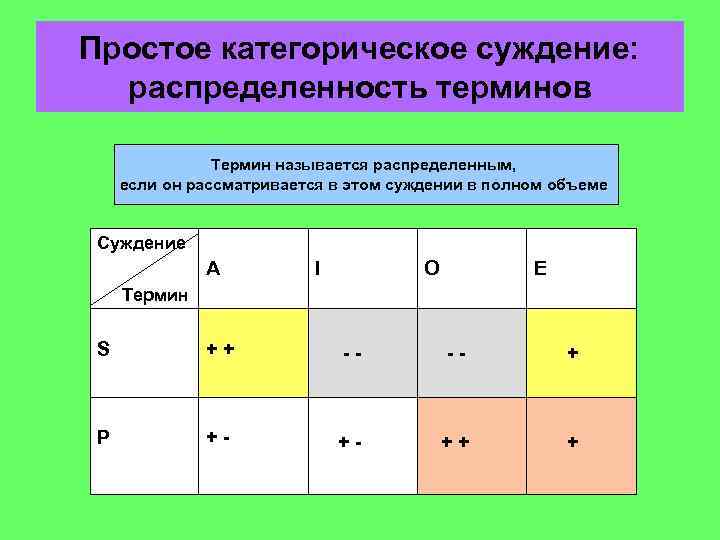
Простое категорическое суждение: распределенность терминов Термин называется распределенным, если он рассматривается в этом суждении в полном объеме Суждение A I O E Термин S ++ -- -- + P +- +- ++ +

Сложное суждение: виды Соединительное суждение конъюнкция – p / q Условное суждение импликация – p q Разделительное суждение дизъюнкция – p / q Суждение эквивалентности равносильность – p q Строго разделительное суждение строгая дизъюнкция – p -/ q Отрицание суждения p ~p
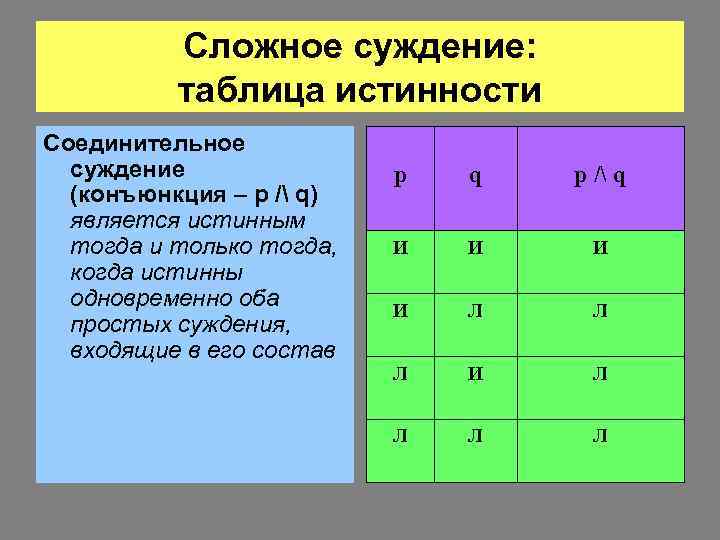
Сложное суждение: таблица истинности Соединительное суждение (конъюнкция – p / q) является истинным тогда и только тогда, когда истинны одновременно оба простых суждения, входящие в его состав p q p / q И И Л Л Л И Л Л
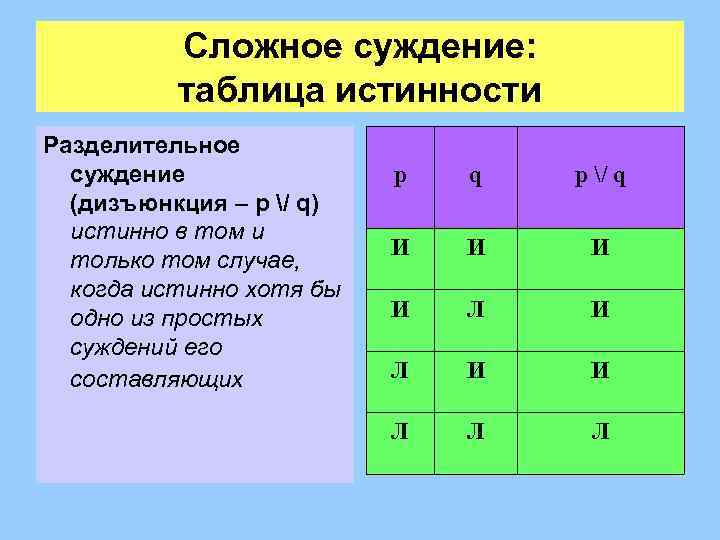
Сложное суждение: таблица истинности Разделительное суждение (дизъюнкция – p / q) истинно в том и только том случае, когда истинно хотя бы одно из простых суждений его составляющих p q p / q И И Л Л Л
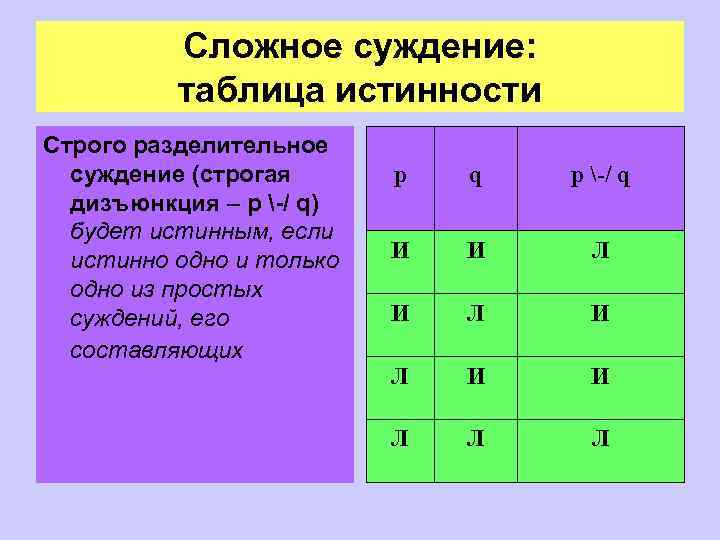
Сложное суждение: таблица истинности Строго разделительное суждение (строгая дизъюнкция – p -/ q) будет истинным, если истинно одно и только одно из простых суждений, его составляющих p q p -/ q И И Л И Л И И Л Л Л
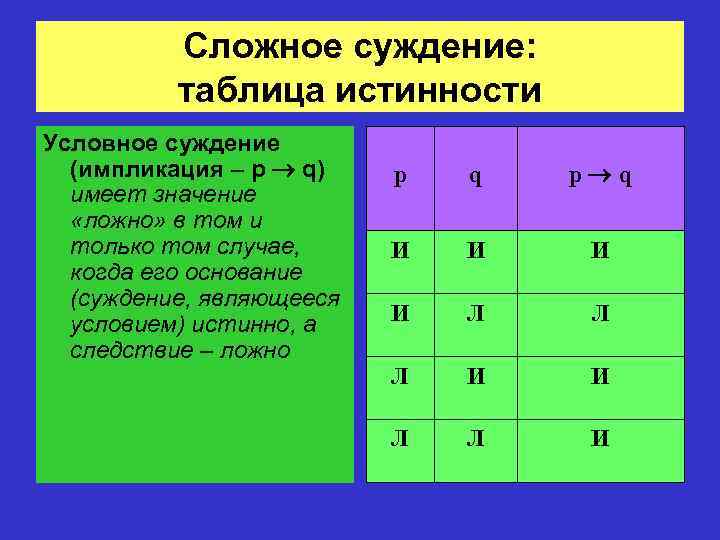
Сложное суждение: таблица истинности Условное суждение (импликация – p q) имеет значение «ложно» в том и только том случае, когда его основание (суждение, являющееся условием) истинно, а следствие – ложно p q И И Л Л Л И И Л Л И
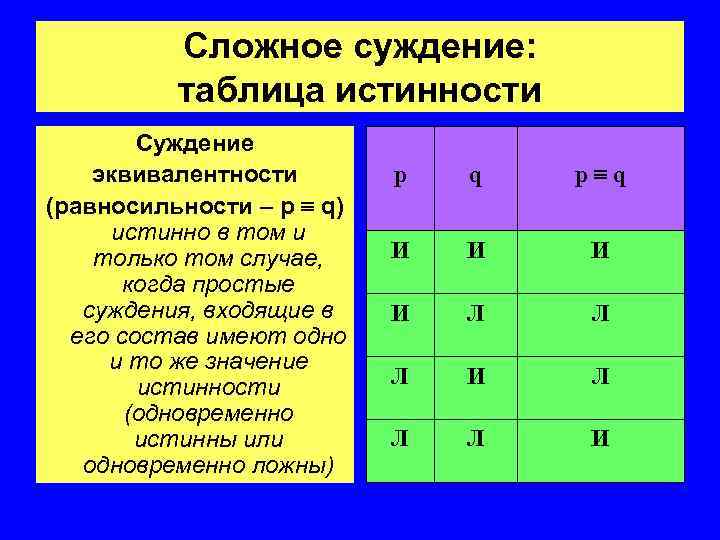
Сложное суждение: таблица истинности Суждение эквивалентности (равносильности – p q) истинно в том и только том случае, когда простые суждения, входящие в его состав имеют одно и то же значение истинности (одновременно истинны или одновременно ложны) p q И И Л Л Л И
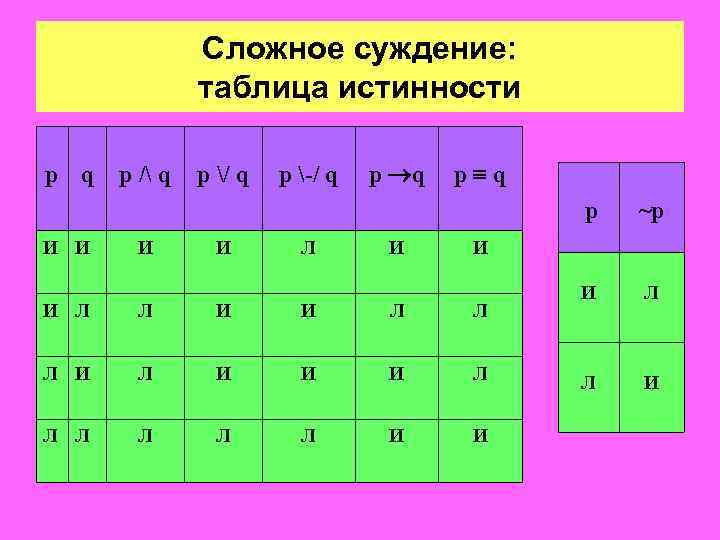
Сложное суждение: таблица истинности p q p / q p / q p -/ q p q p И И Л И ~p И Л Л И И Л Л Л И И
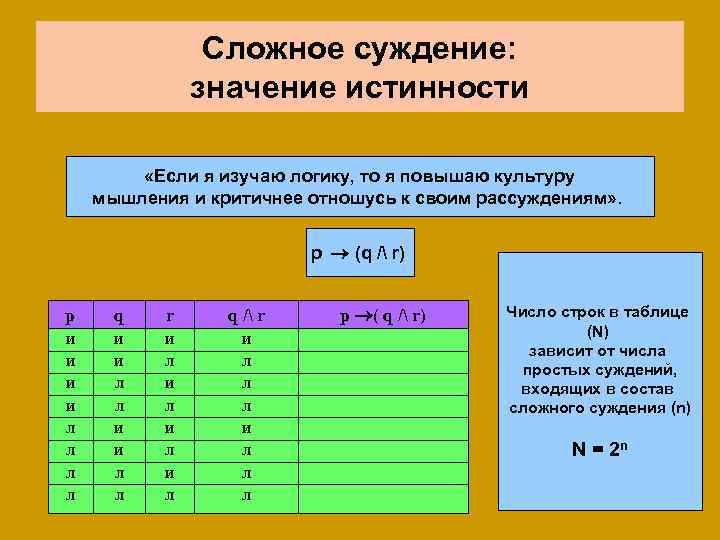
Сложное суждение: значение истинности «Если я изучаю логику, то я повышаю культуру мышления и критичнее отношусь к своим рассуждениям» . p (q / r) p q r q / r И И И Л Л И Л И Л Л И И И Л Л Л Л Л Число строк в таблице (N) зависит от числа простых суждений, входящих в состав сложного суждения (n) И Л p ( q / r) N = 2 n
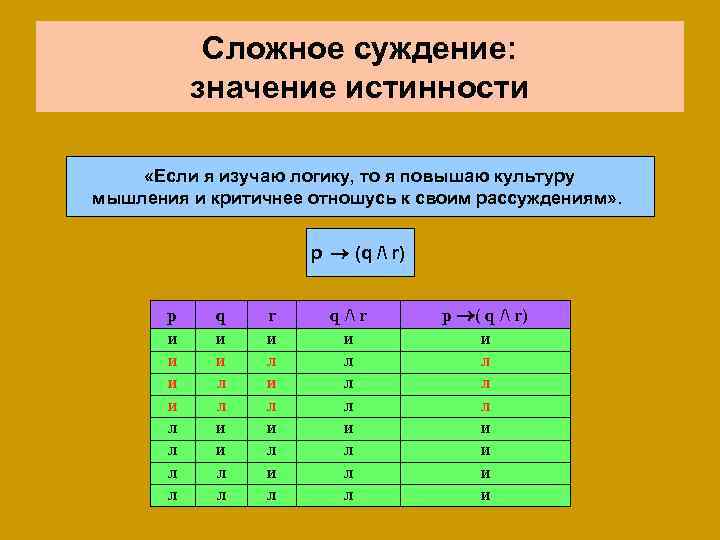
Сложное суждение: значение истинности «Если я изучаю логику, то я повышаю культуру мышления и критичнее отношусь к своим рассуждениям» . p (q / r) p q r q / r p ( q / r) И И И И Л Л Л И Л Л Л И И Л И Л Л И
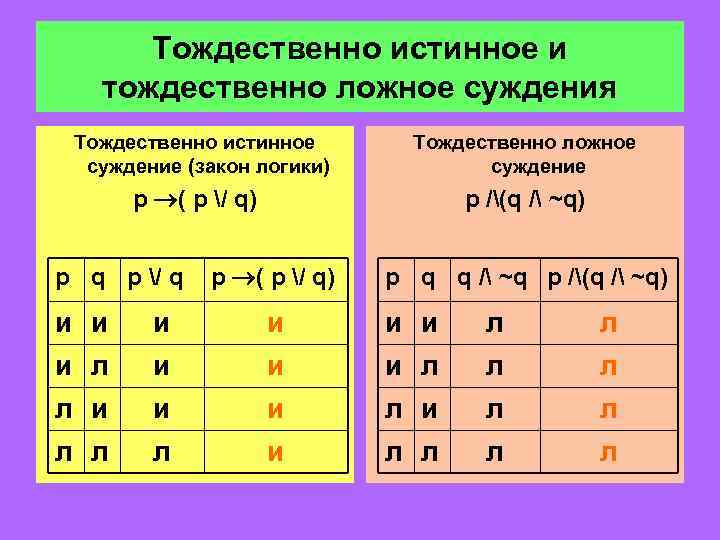
Тождественно истинное и тождественно ложное суждения Тождественно истинное суждение (закон логики) Тождественно ложное суждение p ( p / q) p q p / q p /(q / ~q) p ( p / q) p q q / ~q p /(q / ~q) и и и л л и и и л л л и л л

Отрицание сложных суждений Отрицанием сложного суждения, представляющего только конъюнкцию или только нестрогую дизъюнкцию, будет суждение, состоящее из отрицаний тех же самых простых суждений, соединенных между собой логическими союзами, противоположными первоначальным (конъюнкция заменяется нестрогой дизъюнкцией, а нестрогая дизъюнкция – конъюнкцией). Формулы 1) и 2) при этом называют законами де Моргана 1) ~(p q) ~p ~q И 2) ~(r l) ~r ~l 3) ~(p q r ~l) ~p ~q ~r l 4) ~(p → q) p ~q

Отрицание сложных суждений При необходимости получить отрицание какого-либо сложного высказывания естественного языка, необходимо: 1) сначала формализовать это высказывание, 2) затем получить отрицание этого формального высказывания, и, наконец, 3) «перевести» полученную в результате отрицания формулу на естественный язык Пример: «Если у меня будет свободное время (p) и желание (q), то я прочитаю эту книгу (r)» . 1) (p q) r; 2) ~((p q) r) ≡ (p q) ~r 3) «У меня будет свободное время и желание, но я не прочитаю эту книгу»
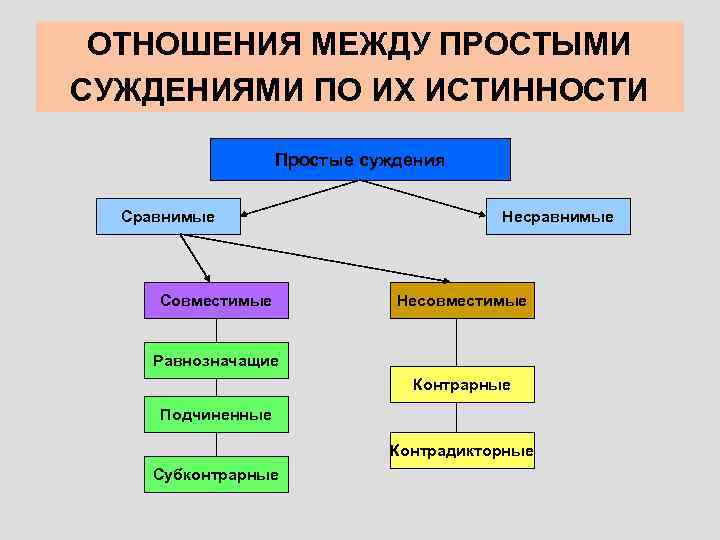
ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ ПО ИХ ИСТИННОСТИ Простые суждения Сравнимые Совместимые Несравнимые Несовместимые Равнозначащие Контрарные Подчиненные Контрадикторные Субконтрарные

ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ ПО ИХ ИСТИННОСТИ Равнозначащие Суждения Основное свойство • выражают одну и ту же мысль, но имеют различную грамматическую форму • одновременно истинны или одновременно ложны Например: «Каждый равносторонний треугольник имеет равные углы» и «У любого правильного треугольника все углы равны другу» . Подчиненные суждения (A – I, E – O) Основное свойство Могут быть одновременно истинными или ложными Следствие Из истинности общего суждения следует истинность частного, а из ложности частного – ложность общего. Обратное неверно Aи → Iи, Eи → Oи Iл → Aл, Oл → Eл

ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ ПО ИХ ИСТИННОСТИ Субконтрарные cуждения (I – O) Свойствo Могут быть одновременно истинными, но не могут быть одновременно ложными Следствие Из ложности одного из них следует истинность второго Iл → Oи Oл → Iи Контрарные суждения (A – E) Свойство Могут быть одновременно ложными, но не могут быть одновременно истинными Следствие Из истинности одного из них следует ложность второго Aи → Eл Eи → Aл
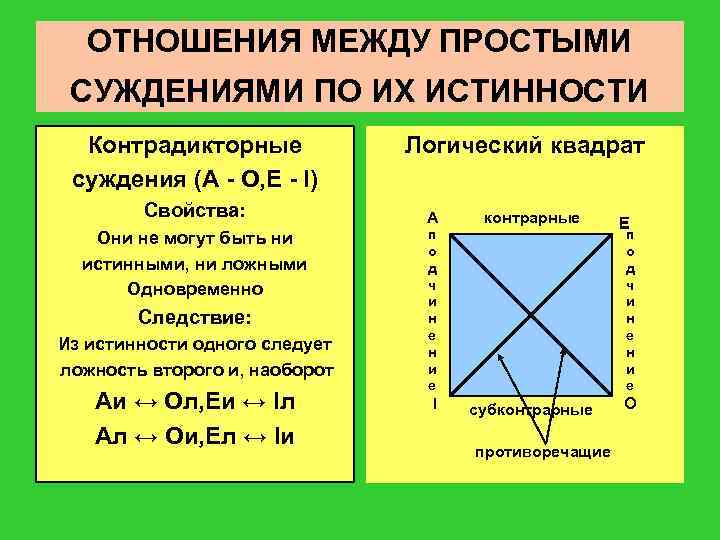
ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ ПО ИХ ИСТИННОСТИ Контрадикторные суждения (A - O, E - I) Свойства: Они не могут быть ни истинными, ни ложными Одновременно Следствие: Из истинности одного следует ложность второго и, наоборот Aи ↔ Oл, Eи ↔ Iл Aл ↔ Oи, Eл ↔ Iи Логический квадрат А контрарные п о д ч и н е н и е I E п о д ч и н е н и е субконтрарные противоречащие O
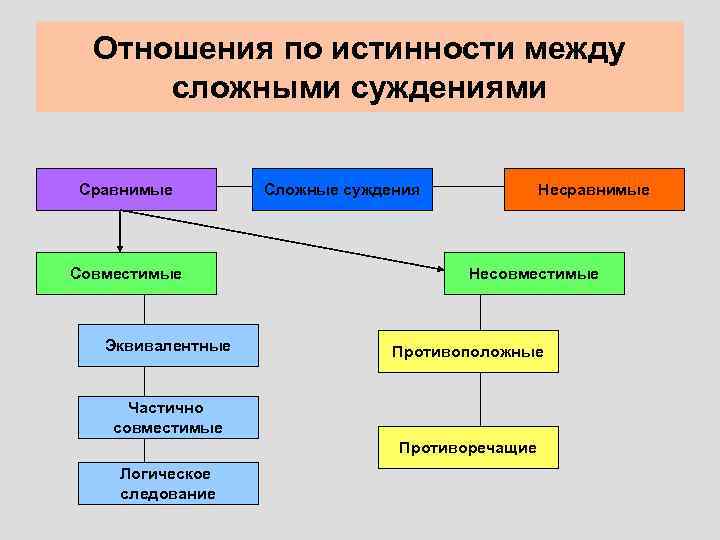
Отношения по истинности между сложными суждениями Сравнимые Совместимые Эквивалентные Сложные суждения Несравнимые Несовместимые Противоположные Частично совместимые Противоречащие Логическое следование
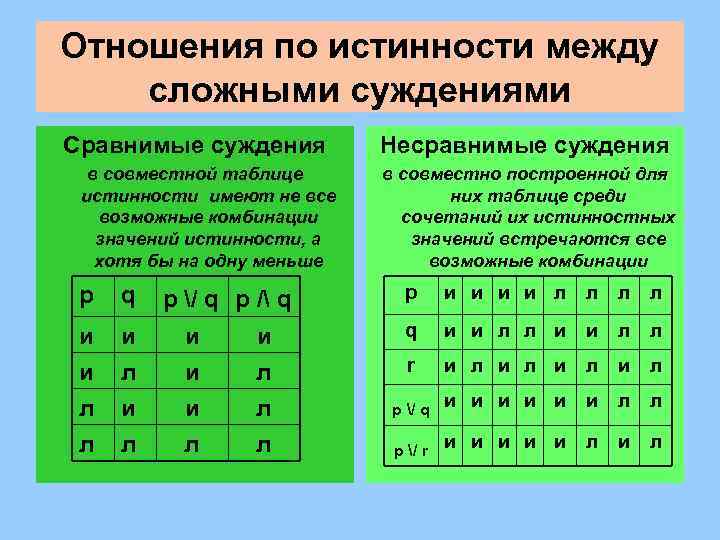
Отношения по истинности между сложными суждениями Сравнимые суждения в совместной таблице истинности имеют не все возможные комбинации значений истинности, а хотя бы на одну меньше p q и и л л и л p / q p / q и и и л л л Несравнимые суждения в совместно построенной для них таблице среди сочетаний их истинностных значений встречаются все возможные комбинации p и и л л q и и л л r и л и л p / q и и и л л p / r и и и л

Отношения по истинности между сложными суждениями Совместимые суждения таблицы их истинности имеют одни и те же значения Несовместимые суждения таблицы их истинности имеют разные значения
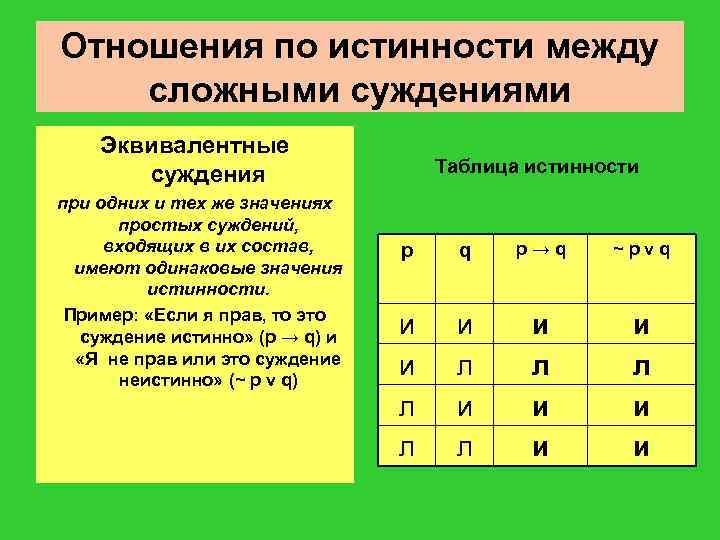
Отношения по истинности между сложными суждениями Эквивалентные суждения при одних и тех же значениях простых суждений, входящих в их состав, имеют одинаковые значения истинности. Пример: «Если я прав, то это суждение истинно» (p → q) и «Я не прав или это суждение неистинно» (~ p v q) Таблица истинности p q p→q ~pvq и и л л и л и и
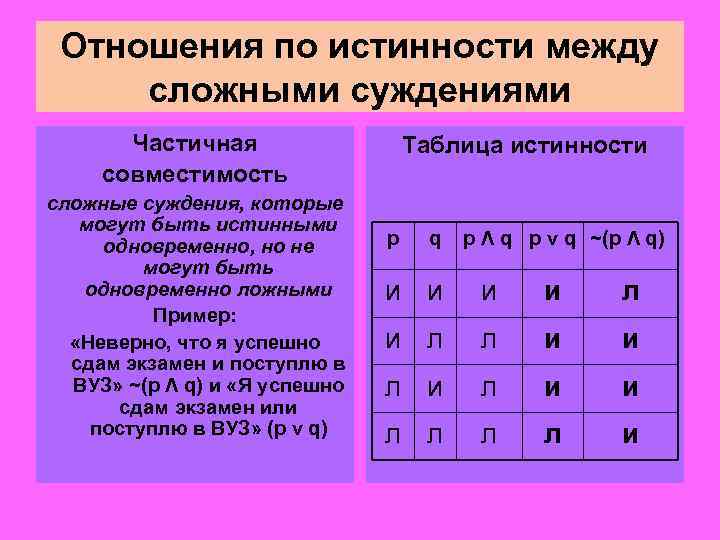
Отношения по истинности между сложными суждениями Частичная совместимость сложные суждения, которые могут быть истинными одновременно, но не могут быть одновременно ложными Пример: «Неверно, что я успешно сдам экзамен и поступлю в ВУЗ» ~(p Λ q) и «Я успешно сдам экзамен или поступлю в ВУЗ» (p v q) Таблица истинности p q p Λ q p v q ~(p Λ q) и и л и л л и и л л и

Отношения по истинности между сложными суждениями Логическое следование сложные суждения, связь между которыми такова, что при истинности первого из них второе не может быть ложным Пример: «Я выучу теорию и буду использовать ее на практике» и «Если я выучу теорию, то буду использовать ее на практике» Таблица истинности p q pΛq p→q и и и л л л и
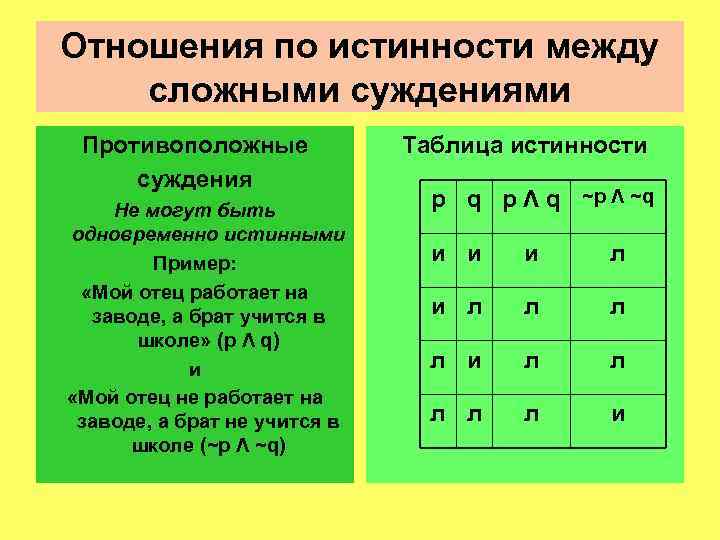
Отношения по истинности между сложными суждениями Противоположные суждения Не могут быть одновременно истинными Пример: «Мой отец работает на заводе, а брат учится в школе» (p Λ q) и «Мой отец не работает на заводе, а брат не учится в школе (~p Λ ~q) Таблица истинности p q p Λ q ~p Λ ~q и и и л л л л и

Отношения по истинности между сложными суждениями Противоречащие суждения не могут быть одновременно ни истинными, ни ложными Пример: «Я сдал экзамен на отлично и поступил в институт» (p Λ q) и «Я не сдал экзамен на отлично или не поступил в институт» (~p v ~q) Таблица истинности p q p Λ q ~p v ~q и и и л л и л и л л л и
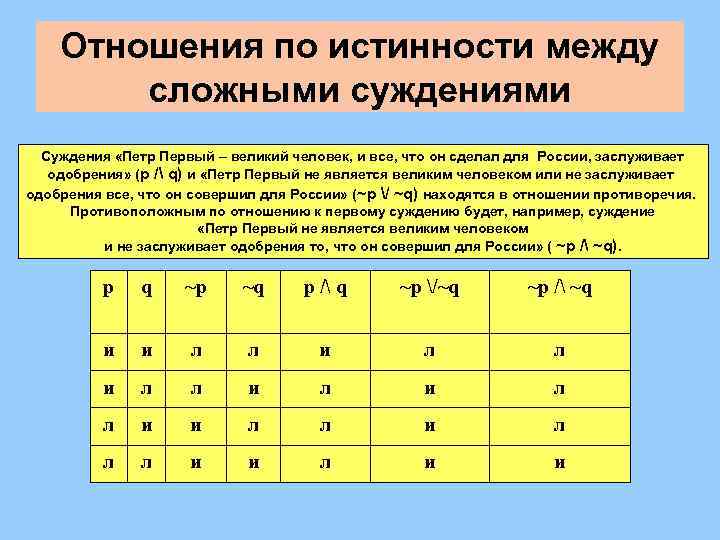
Отношения по истинности между сложными суждениями Суждения «Петр Первый – великий человек, и все, что он сделал для России, заслуживает одобрения» (p / q) и «Петр Первый не является великим человеком или не заслуживает одобрения все, что он совершил для России» (~p / ~q) находятся в отношении противоречия. Противоположным по отношению к первому суждению будет, например, суждение «Петр Первый не является великим человеком и не заслуживает одобрения то, что он совершил для России» ( ~p / ~q). p q ~p ~q p / q ~p /~q ~p / ~q и и л л и л л и и л л л и и
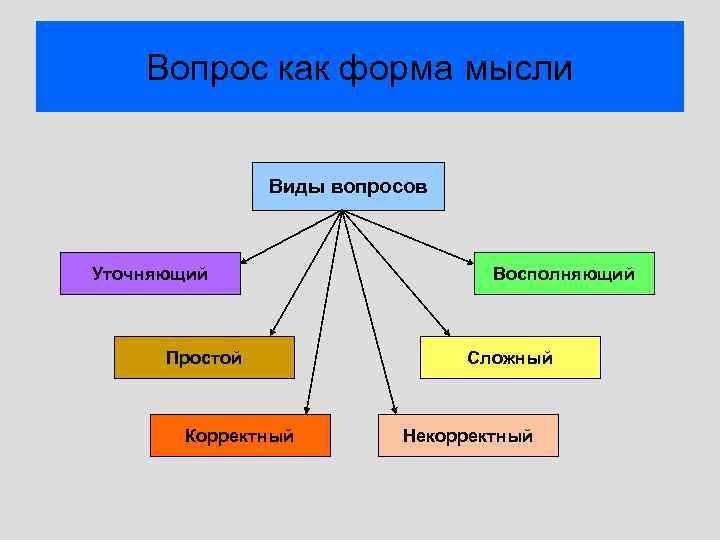
Вопрос как форма мысли Виды вопросов Уточняющий Простой Корректный Восполняющий Сложный Некорректный
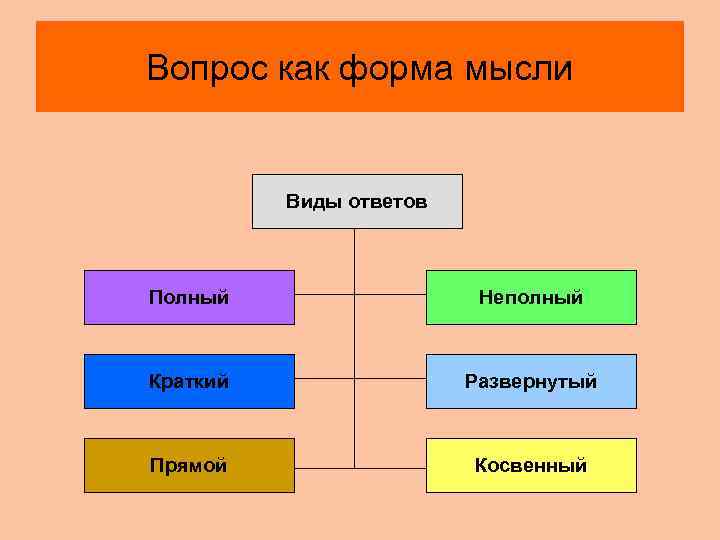
Вопрос как форма мысли Виды ответов Полный Неполный Краткий Развернутый Прямой Косвенный
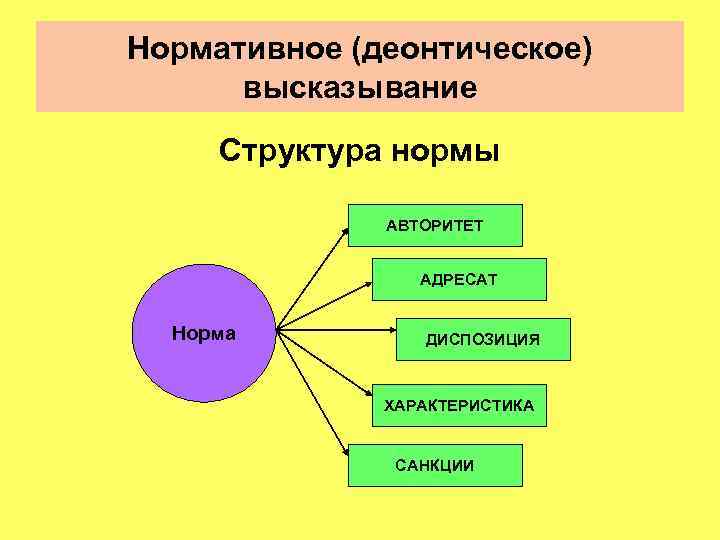
Нормативное (деонтическое) высказывание Структура нормы АВТОРИТЕТ АДРЕСАТ Норма ДИСПОЗИЦИЯ ХАРАКТЕРИСТИКА САНКЦИИ
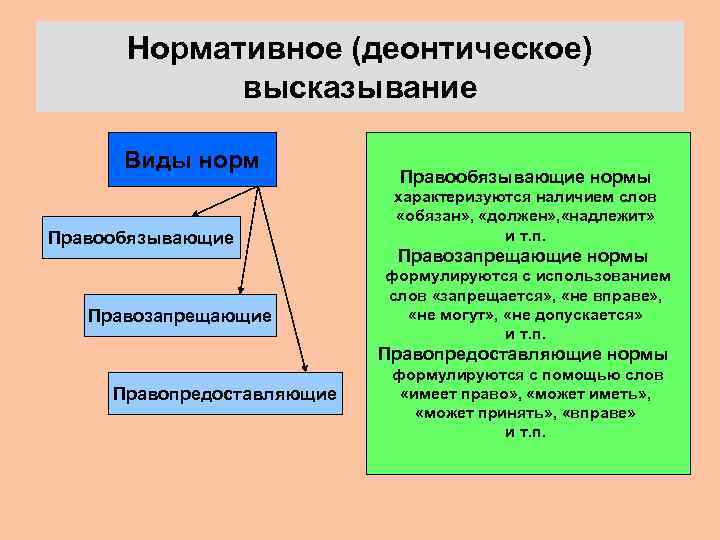
Нормативное (деонтическое) высказывание Виды норм Правообязывающие Правозапрещающие Правообязывающие нормы характеризуются наличием слов «обязан» , «должен» , «надлежит» и т. п. Правозапрещающие нормы формулируются с использованием слов «запрещается» , «не вправе» , «не могут» , «не допускается» и т. п. Правопредоставляющие нормы Правопредоставляющие формулируются с помощью слов «имеет право» , «может иметь» , «может принять» , «вправе» и т. п.

Тема IV. Умозаключение IV. 1. Общая характеристика умозаключений IV. 2. 1. Умозаключения на основе связи между суждениями. IV. 2. 1. 1. Прямые умозаключения IV. 2. 1. 2. Непрямые умозаключения IV. 2. 2. Умозаключения на основе связи между терминами простых суждений. Силлогизмы и их классификация. IV. 2. 2. 1. Непосредственные силлогизмы. IV. 2. 2. 2. Опосредованные силлогизмы. Простой категорический силлогизм IV. 2. 2. 3. Энтимема IV. 2. 2. 4. Полисиллогизм и сорит IV. 3. Недедуктивные умозаключения. IV. 3. 1. Индуктивные умозаключения. IV. 3. 1. 1. Полная индукция. IV. 3. 1. 2. Популярная индукция (Неполная индукция через простое перечисление). IV. 3. 1. 3. Научная индукция. IV. 3. 2. Аналогия

Умозаключение Общая характеристика. Структура • Умозаключение – это мыслительный процесс (рассуждение), в ходе которого из одного или нескольких суждений, называемых посылками, выводится новое суждение, называемое следствием или заключением Структура умозаключения: (A 1 A 2 A 3 . . . Ak) B или A 1, A 2, A 3, . . . , Ak B
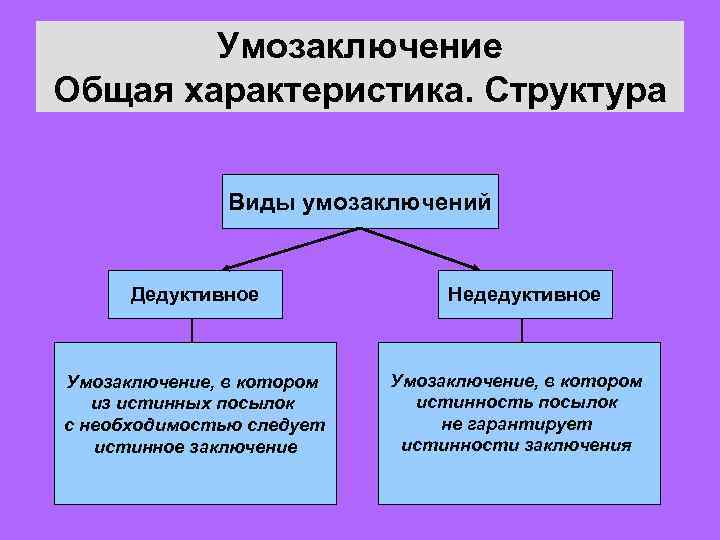
Умозаключение Общая характеристика. Структура Виды умозаключений Дедуктивное Умозаключение, в котором из истинных посылок с необходимостью следует истинное заключение Недедуктивное Умозаключение, в котором истинность посылок не гарантирует истинности заключения
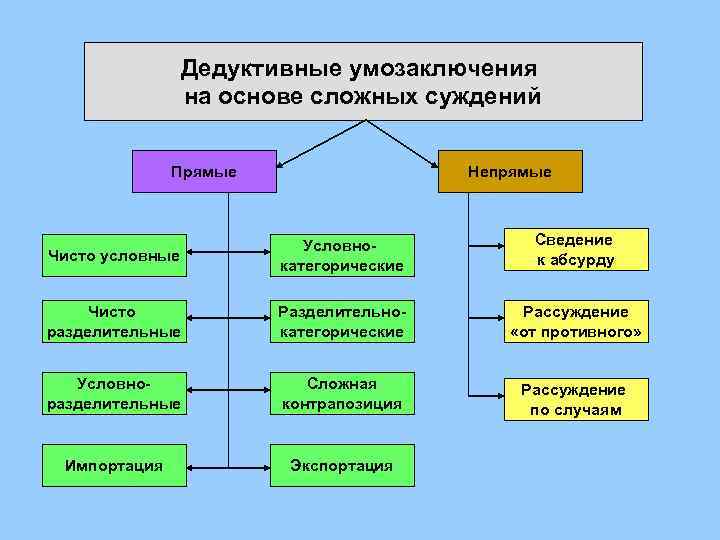
Дедуктивные умозаключения на основе сложных суждений Прямые Непрямые Чисто условные Условнокатегорические Сведение к абсурду Чисто разделительные Разделительнокатегорические Рассуждение «от противного» Условноразделительные Сложная контрапозиция Рассуждение по случаям Импортация Экспортация
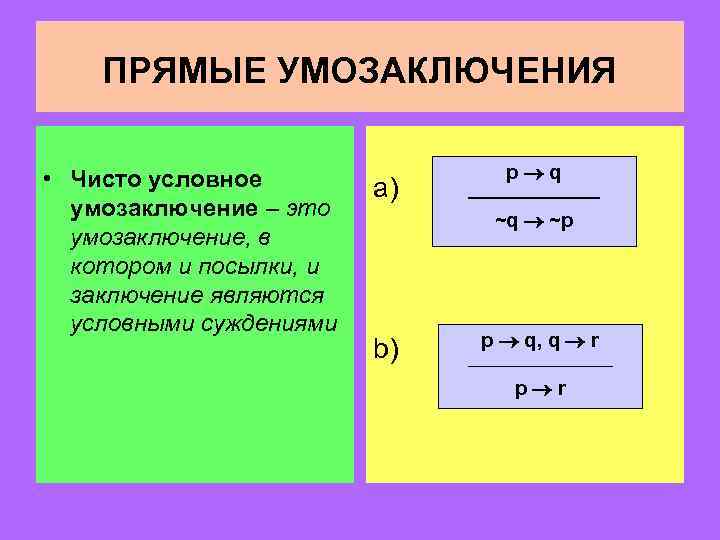
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ • Чисто условное умозаключение – это умозаключение, в котором и посылки, и заключение являются условными суждениями a) p q ~q ~p b) p q, q r p r
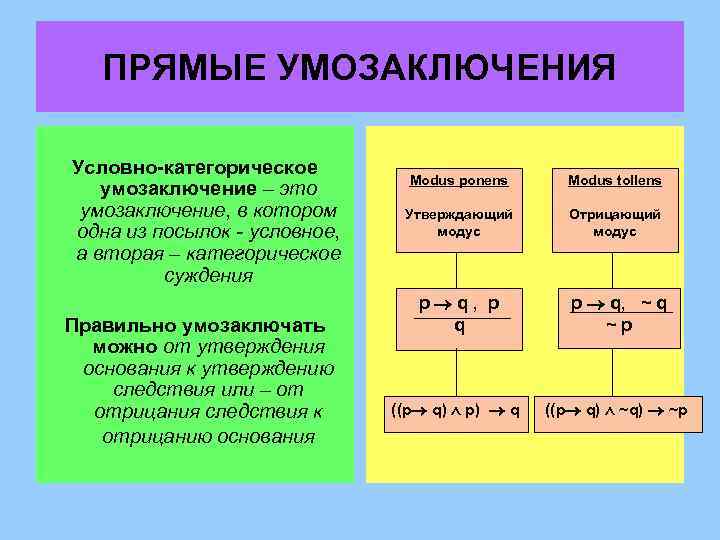
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Условно-категорическое умозаключение – это умозаключение, в котором одна из посылок - условное, а вторая – категорическое суждения Правильно умозаключать можно от утверждения основания к утверждению следствия или – от отрицания следствия к отрицанию основания Modus ponens Modus tollens Утверждающий модус Отрицающий модус p q, p q p q, ~ q ~p ((p q) p) q ((p q) ~p

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Условно-категорическое умозаключение Вероятностные модусы p q, q p p q, ~ p ~q ((p q) p ((p q) ~ p) ~ q
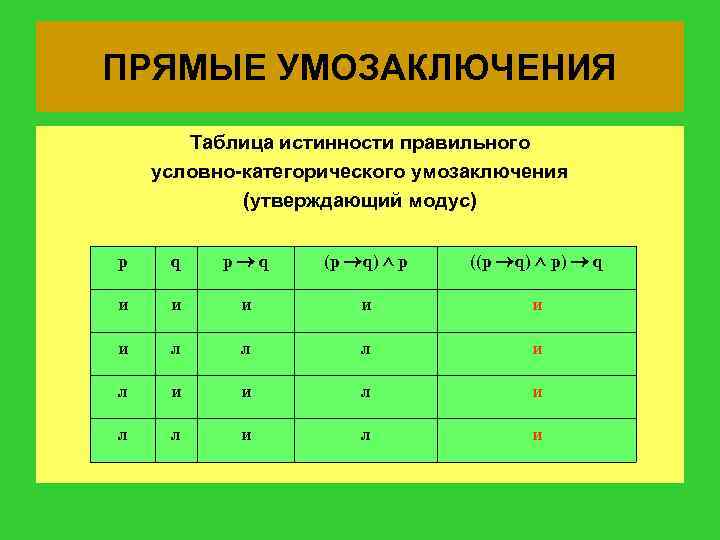
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Таблица истинности правильного условно-категорического умозаключения (утверждающий модус) p q (p q) p ((p q) p) q и и и л л л и и л л и

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Таблица истинности вероятностного условно-категорического умозаключения (утверждающий модус) p q (p q) q ((p q) p и и и л л л и
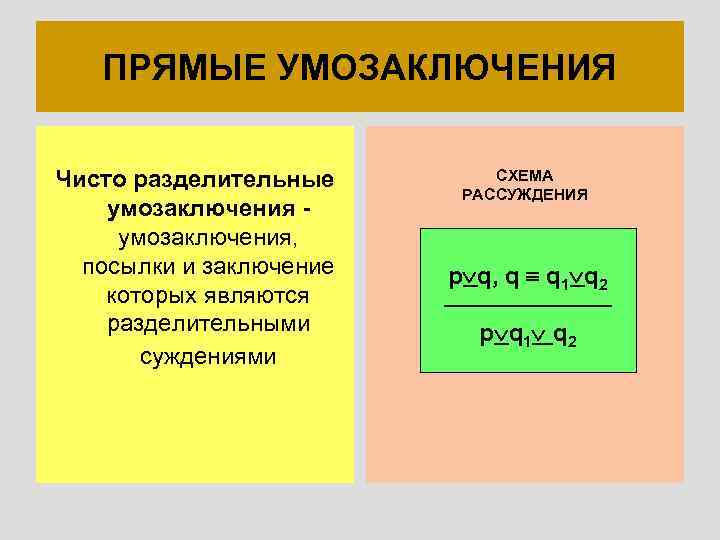
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Чисто разделительные умозаключения, посылки и заключение которых являются разделительными суждениями СХЕМА РАССУЖДЕНИЯ p q, q q 1 q 2 p q 1 q 2
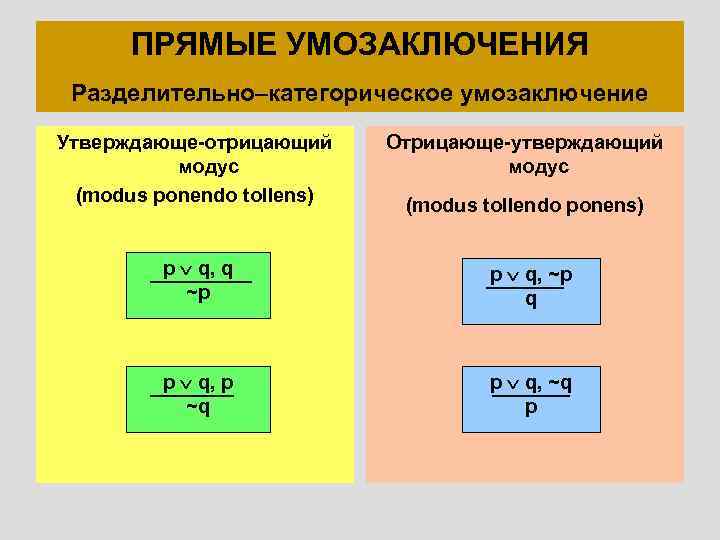
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Разделительно–категорическое умозаключение Утверждающе-отрицающий модус (modus ponendo tollens) Отрицающе-утверждающий модус (modus tollendo ponens) p q, q ~p p q, ~p q p q, p ~q p q, ~q p
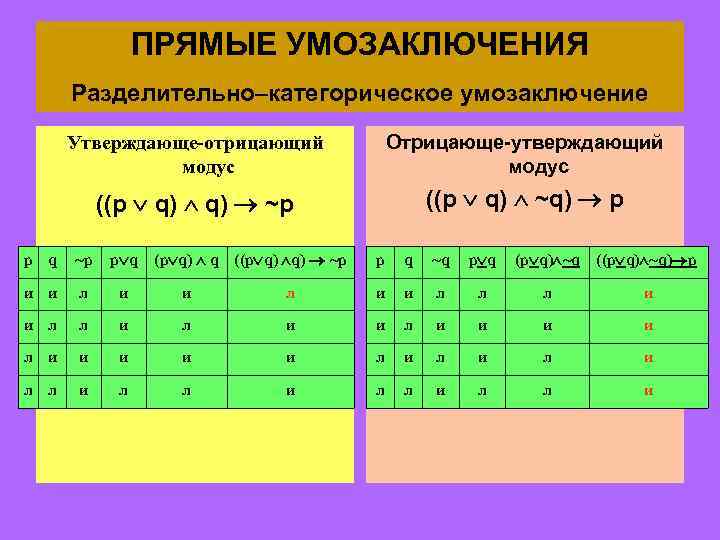
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Разделительно–категорическое умозаключение Утверждающе-отрицающий модус Отрицающе-утверждающий модус ((p q) ~p ((p q) ~q) p (p q) q ((p q) q) ~p p q p q ~q p q (p q) ~q ((p q) ~q) p и и л л л и и л и и и и и л и л л и л л и

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Разделительно–категорическое умозаключение Разделительно-категорическое суждение с тремя альтернативами «Пожар в магазине мог возникнуть в результате самовозгорания (p), неосторожного обращения с огнем (q) или поджога (r). Расследованием установлено, что причиной пожара стало неосторожное обращение с огнем (q). Значит, пожар в магазине не в результате самовозгорания ( p) и не в результате поджога ( r)» . p q r, q ~p ~r
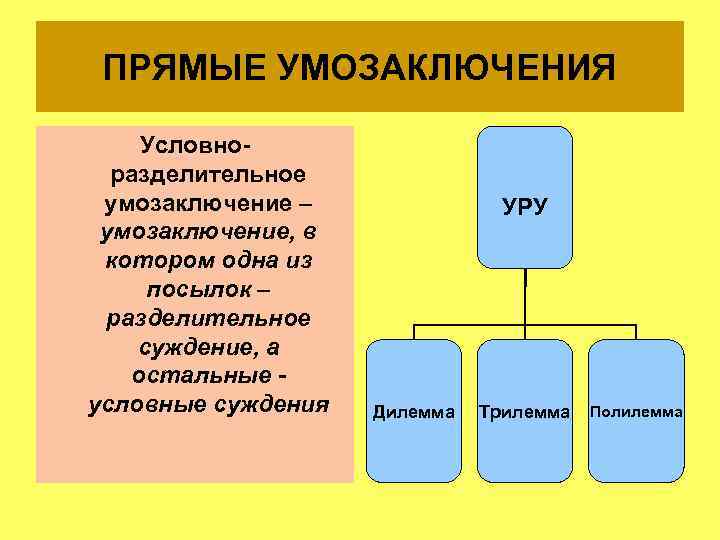
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Условноразделительное умозаключение – умозаключение, в котором одна из посылок – разделительное суждение, а остальные условные суждения УРУ Дилемма Трилемма Полилемма
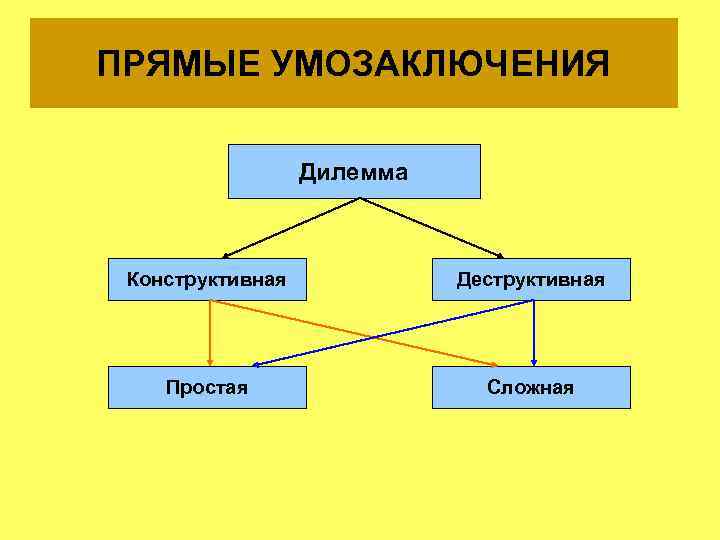
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Дилемма Конструктивная Деструктивная Простая Сложная

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ • Простая конструктивная дилемма p q, r q, p r q • Простая деструктивная дилемма p q, p r, ~ q ~ r ~p

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ • Сложная конструктивная дилемма p q, r l, p r q l • Сложная деструктивная дилемма p q, r l, ~ q ~l ~p ~r
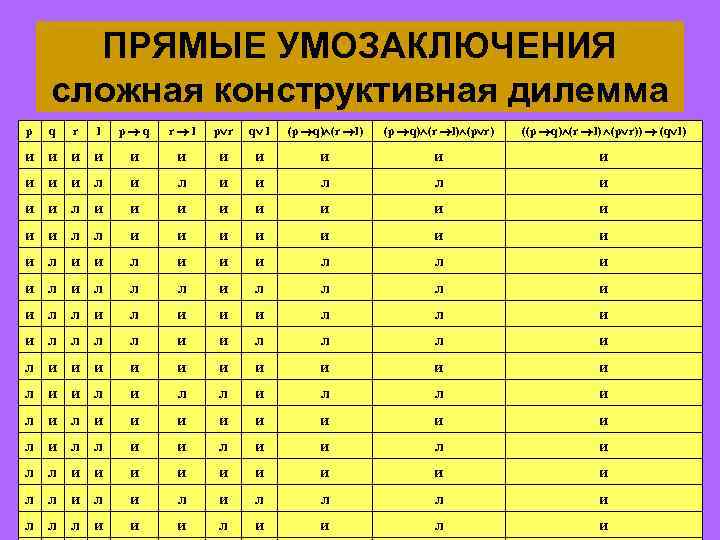
ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ сложная конструктивная дилемма p q r l p r q l (p q) (r l) (p r) ((p q) (r l) (p r)) (q l) и и и и л и и л л и и и и л л и и и и л л и и л л л и и л л и и и л л л л и и и и и и л и л и и и и и л л и и л и л л и и и и и л л и л и л л л и и и л и p q r l

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Трилемма p q, l m, k n, q m n p l k ((p q) (l m) (k n) (q m n)) (p l k)

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Сложная контрапозиция (p q) r (p ~r) ~q «Если я освою Windows и Excel (p q), то меня могут взять на работу в этой фирме (r). Следовательно, если я освою Windows (p), но меня не возьмут на работу в эту фирму ( r), то это значит, что я не освоил Excel ( q), » .

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Импортация p (q r) (p q) r «Если я сдам этот экзамен не ниже, чем на «хорошо» (p), то если хотя бы один из моих конкурентов сдаст его не выше, чем на «хорошо» (q), у меня есть шанс поступить в университет (r). Значит, если я сдам этот экзамен не ниже, чем на «хорошо» (p) и ни один из моих конкурентов не получит оценки «отлично» (q), то я имею шанс поступить в университет (r)» .

ПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Экспортация (p q) r p (q r) «Если некоторое число кратно пяти (p) и, одновременно, кратно двум (q), то это число обязательно оканчивается на ноль (r). Следовательно, если некоторое число кратно пяти (p), то если оно кратно двум (q), оно обязательно оканчивается нулем (r)» .
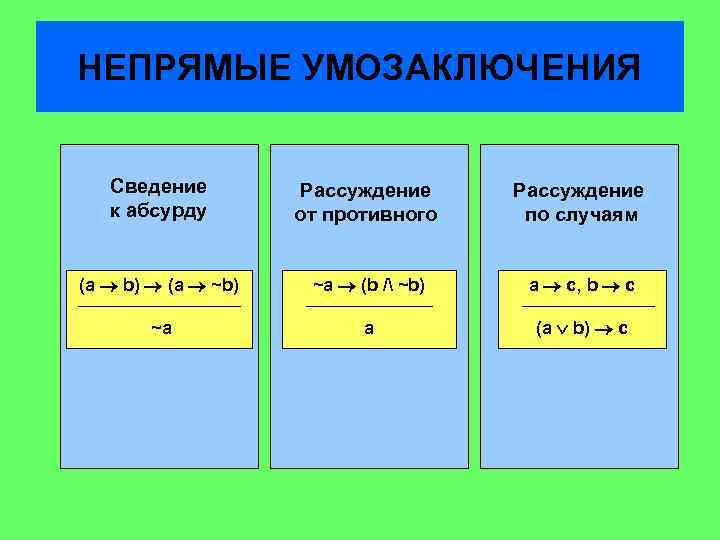
НЕПРЯМЫЕ УМОЗАКЛЮЧЕНИЯ Сведение к абсурду Рассуждение от противного Рассуждение по случаям (а b) (а ~b) ~а (b / ~b) а с, b с ~а а (а b) с
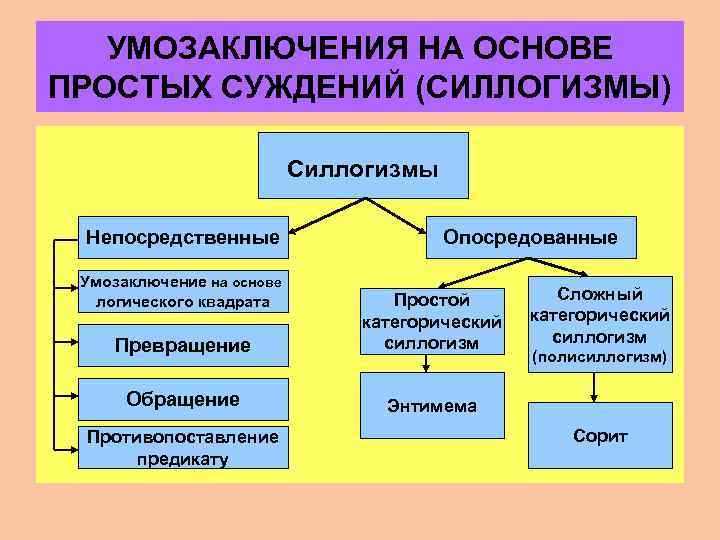
УМОЗАКЛЮЧЕНИЯ НА ОСНОВЕ ПРОСТЫХ СУЖДЕНИЙ (СИЛЛОГИЗМЫ) Силлогизмы Непосредственные Умозаключение на основе логического квадрата Опосредованные Превращение Простой категорический силлогизм Обращение Сложный категорический силлогизм Энтимема Противопоставление предикату (полисиллогизм) Сорит
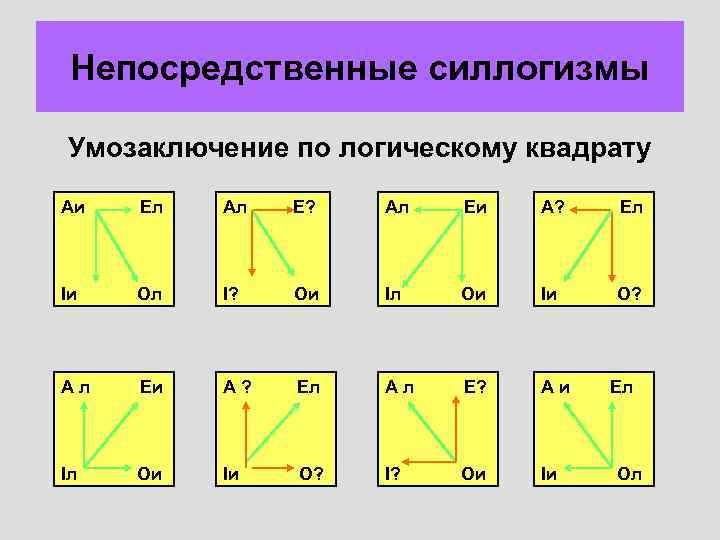
Непосредственные силлогизмы Умозаключение по логическому квадрату Аи Ел Ал Е? Ал Еи А? Ел Iи Ол I? Ои Iл Ои Iи О? Ал Еи А? Ел Ал Е? Аи Iл Ои Iи О? I? Ои Iи Ел Ол

Непосредственные силлогизмы Превращение Схема превращения A E: Все S есть P Ни одно S не есть не-P I O: Некоторые S есть P Некоторые S не есть не-P E A: Ни одно S не есть P Все S есть не-P O I: Некоторые S не есть P Некоторые S есть не-P Алгоритм превращения - Записать исходное суждение (посылку) в четкой логической форме; - Изменить качество суждения: поменять связку «есть» на связку «не есть» (или наоборот); - На место предиката поставить понятие, противоречащее предикату посылки.

Непосредственные силлогизмы Обращение Схема обращения E E: Ни одно S не есть P Ни одно P не есть S I а) Некоторые S есть P Некоторые P есть S (S и P не распределены) б) Некоторые S есть P Все P есть S (P не распределен) Алгоритм обращения • • • A а)Все S есть P Некоторые P есть S (P не распределен) б) Все S есть P Все P есть S (P распределен) О : не обращается • Привести исходное суждение (посылку) к четкой логической форме; Установить его вид и распределенность терминов; На место субъекта заключения поставить предикат посылки, а на место предиката заключения – ее субъект, оставив при этом без изменения логическую связку между ними. Исходя из вида сужденияпосылки и распределенности его терминов уточнить количественную характеристику заключения.

Непосредственные силлогизмы Противопоставление предикату Алгоритм противопоставления Схема противопоставления A E: Все S есть P Ни одно не-P не есть S • • E I: Ни одно S не есть P Некоторые не-P есть S O I : Некоторые S не есть P Некоторые не-P есть S I: не противопоставляется предикату. • Записать суждение-посылку в четкой логической форме и установить ее вид); Изменить качественную характеристику суждения, заменив связку «есть» на «не есть» (или наоборот); На место субъекта поставить понятие, противоречащее предикату посылки, а на место предиката – ее субъект.

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Простой категорический силлогизм – дедуктивное умозаключение, в котором из двух простых категорических суждений, имеющих общий термин, выводится новое простое категорическое суждение Все юристы имеют высшее образование Все адвокаты – юристы ________________ Все адвокаты имеют высшее образование

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Субъект заключения называют мéньшим термином и обозначают символом S. Предикат заключения называют бóльшим термином и обозначают символом P. Термин, который содержится в обеих посылках, но отсутствует в заключении, называют средним термином и обозначают символом M. Все юристы (M) имеют высшее образование (P). Все адвокаты (S) – юристы (M). ____________ Все адвокаты (S) имеют высшее образование (P). Все M есть P Все S есть M Все S есть P
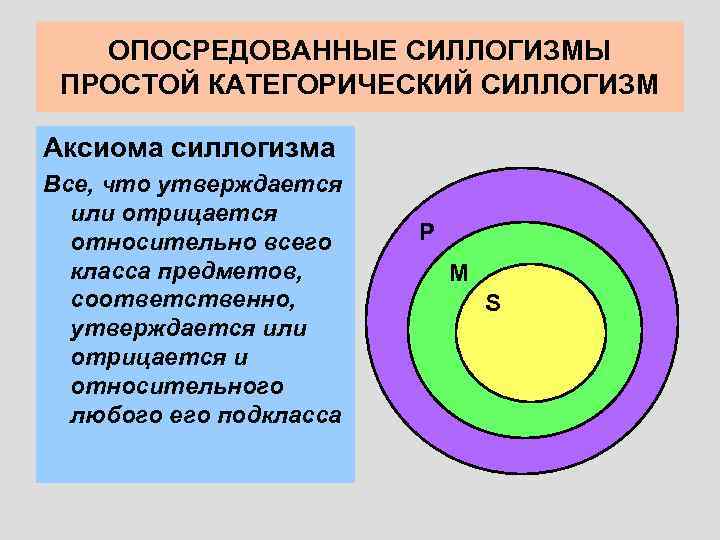
ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Аксиома силлогизма Все, что утверждается или отрицается относительно всего класса предметов, соответственно, утверждается или отрицается и относительного любого его подкласса P M S

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ • • • Правила терминов В силлогизме должно быть только три термина Средний термин должен быть распределен хотя бы в одной из посылок Термин, нераспределенный в посылках, не может быть распределен в заключении • • Правила посылок Из двух отрицательных посылок заключения сделать нельзя Из двух частных посылок заключения сделать нельзя Если одна из посылок частная, то и заключение должно быть частным Если одна из посылок отрицательная, то и заключение должно быть отрицательным
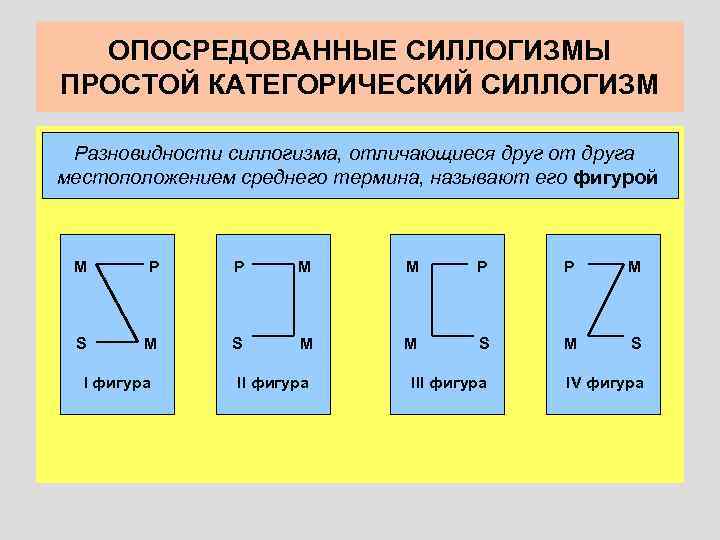
ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Разновидности силлогизма, отличающиеся друг от друга местоположением среднего термина, называют его фигурой М P P М S M M S I фигура III фигура IV фигура

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Специфические (особые) правила фигур • Первая фигура: Большая посылка должна быть общей, а меньшая - утвердительной. Используется в случаях, когда необходимо применить общее положение к частному случаю. • Вторая фигура: Большая посылка должна быть общей, а одна из посылок и заключение – отрицательными. Используется, в основном, как средство опровержения неправильного подчинения. • Третья фигура: Меньшая посылка должна быть утвердительной, а заключение – частное. Может применяться в качестве способа опровержения неверного обобщения. • Четвертая фигура: Общеутвердительных заключений не дает. Используется в рассуждениях весьма редко.

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Модус категорического силлогизма – это его разновидность в зависимости от количественной и качественной характеристики посылок и заключения Все, кто изучает логику (M), повышают критичность мышления (P) - A Некоторые студенты юридического факультета (S) изучают логику (M) - I ____________ Некоторые студенты юридического факультета (S) повышают критичность мышления (P) – I Модус данного силлогизма AII
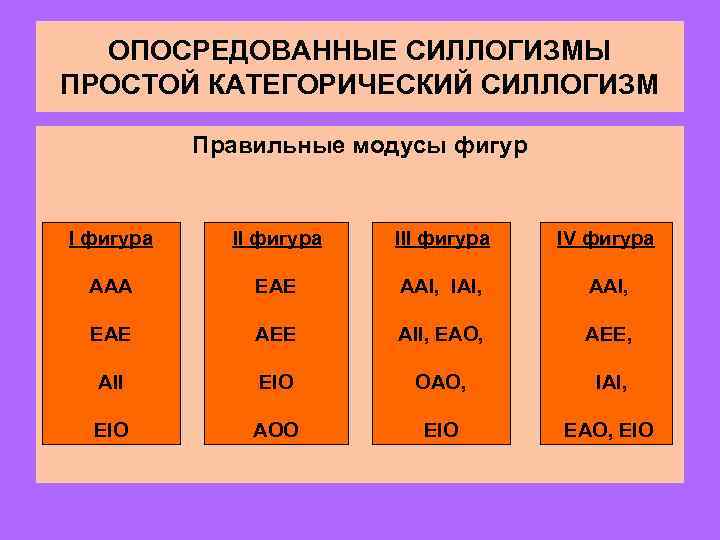
ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Правильные модусы фигур I фигура III фигура IV фигура AAA EAE AAI, IAI, AAI, EAE AEE AII, EAO, AEE, AII EIO OAO, IAI, EIO AOO EIO EAO, EIO

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Силлогизм считается правильным, а его заключение – истинным, если его модус соответствует одному из правильных модусов фигуры, структуру которой повторяет проверяемый силлогизм. Пример: Все учащиеся нашей группы (M) изучают логику (P). Все учащиеся нашей группы (M) – будущие юристы (S). __________ Все будущие юристы (S) изучают логику (P) Фигура III - M-P M-S, Модус – AAA. Отсутствует среди правильных модусов III фигуры. Следовательно, силлогизм неправильный, а истинность его следствия сомнительна.
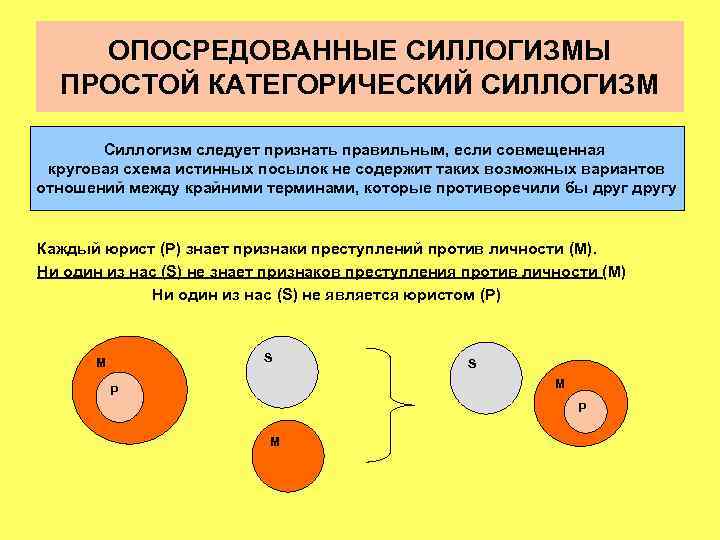
ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Силлогизм следует признать правильным, если совмещенная круговая схема истинных посылок не содержит таких возможных вариантов отношений между крайними терминами, которые противоречили бы другу Каждый юрист (P) знает признаки преступлений против личности (M). Ни один из нас (S) не знает признаков преступления против личности (M) Ни один из нас (S) не является юристом (P) S M P P M
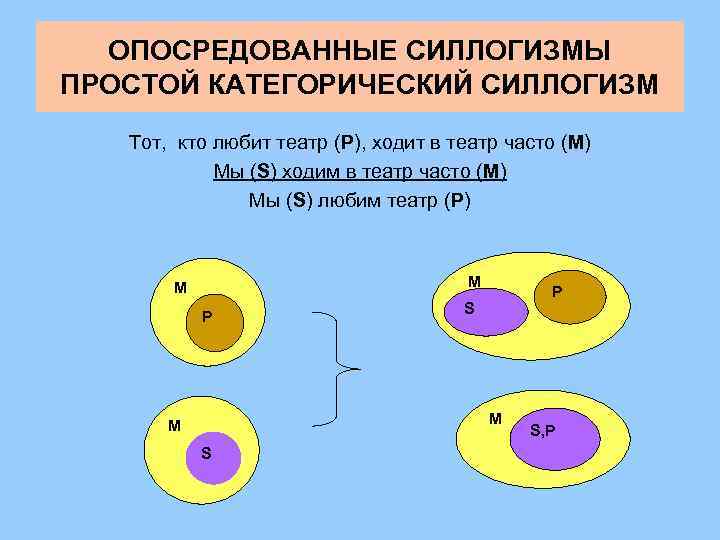
ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ Тот, кто любит театр (P), ходит в театр часто (M) Мы (S) ходим в театр часто (M) Мы (S) любим театр (P) M М Р P S M М S S, P

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ СОКРАЩЕННЫЙ ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ ЭНТИМЕМА категорический силлогизм, в котором пропущена одна из посылок или заключение - Всякая ложь (M) безнравственна (P), значит и лесть (S) безнравственна (P) - Любой человек, причиняющий зло животным (M), не любит их (P), а этот человек (S) причиняет зло животным (M)

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ СЛОЖНЫЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ (ПОЛИСИЛЛОГИЗМ) Полисиллогизм – это сложный силлогизм, состоящий из двух или более простых силлогизмов, связанных между собой таким образом, что заключение каждого предыдущего силлогизма становится посылкой следующего силлогизма Всякий параллелограмм (A) – четырехугольник (B). Всякий ромб (C) – параллелограмм (A). Всякий ромб (C) – четырехугольник (B). Всякий квадрат (D) – ромб (C). Всякий квадрат (D) – четырехугольник (B).

ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ СЛОЖНЫЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ (ПОЛИСИЛЛОГИЗМ) Прогрессивный Все А суть В. Все С суть А. Все С суть В. Все D суть С. Все D суть В. Регрессивный Все А суть В. Все В суть С. Все А суть С. Все С суть D Все А суть D.
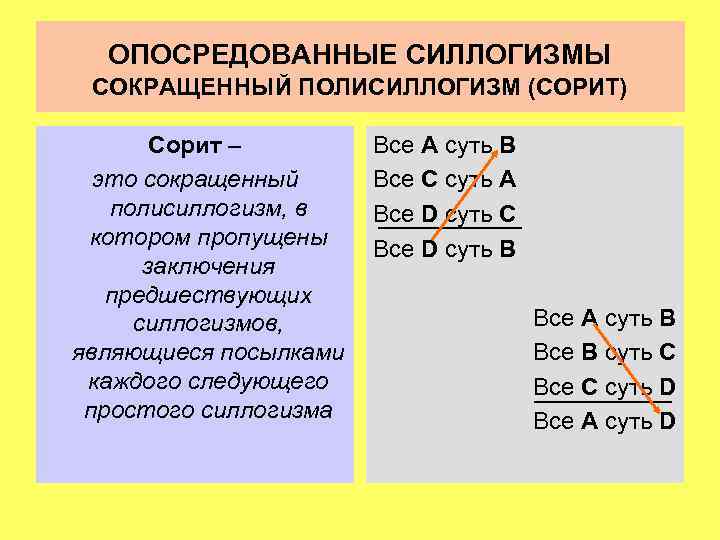
ОПОСРЕДОВАННЫЕ СИЛЛОГИЗМЫ СОКРАЩЕННЫЙ ПОЛИСИЛЛОГИЗМ (СОРИТ) Сорит – это сокращенный полисиллогизм, в котором пропущены заключения предшествующих силлогизмов, являющиеся посылками каждого следующего простого силлогизма Все А суть В Все С суть А Все D суть С Все D суть В Все А суть В Все B суть C Все C суть D Все A суть D
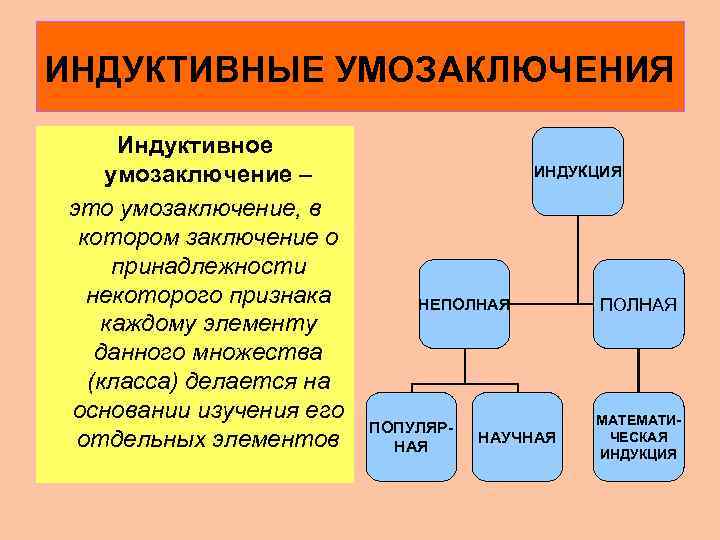
ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Индуктивное умозаключение – это умозаключение, в котором заключение о принадлежности некоторого признака каждому элементу данного множества (класса) делается на основании изучения его отдельных элементов ИНДУКЦИЯ НЕПОЛНАЯ ПОПУЛЯРНАЯ НАУЧНАЯ ПОЛНАЯ МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Схема рассуждения ПОЛНАЯ ИНДУКЦИЯ Умозаключение, в котором общий вывод о принадлежности (непринадлежности) некоторого признака Р всем элементам изучаемого класса делается на основании установления факта принадлежности (непринадлежности) этого признака каждому элементу данного класса Элемент х1 имеет свойство Р. Элемент х2 имеет свойство Р. Элемент х3 имеет свойство Р. …. …. . Элемент хk имеет свойство Р. Все элементы х принадлежат классу М, который включает ровно k элементов. _____________ Все элементы х, принадлежащие классу М, имеют свойство Р.

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ Математическая индукция – это умозаключение, основанное на принципе: утверждение P(x), зависящее от натурального параметра x, считается доказанным, если доказано P(1) и для любого натурального n из предположения, что верно P(n), с необходимостью следует, что верно P(n+1) Алгоритм рассуждения 1 шаг: Устанавливают (доказывают) что некоторое свойство P присуще первому числу (элементу) ряда - P(1); 2 шаг: Делают предположение о том, что это свойство присуще какому-то произвольному числу (элементу) - P(k); 3 шаг: Доказывают, что при этом предположении свойство P присуще следующему числу (элементу), т. е. P(k+1). 4 шаг: Делается общее заключение о том, что свойство P присуще всем числам ряда (элементам класса), т. е. P(n) или x P(x)

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ НЕПОЛНАЯ ИНДУКЦИЯ Популярная индукция (индукция через простое перечисление) – вид неполной индукции, где заключение о принадлежности (не принадлежности) некоторого признака всем элементам данного множества делается на основании того, что этот признак обнаруживается (не обнаруживается) лишь у некоторых произвольно взятых элементов этого множества при условии отсутствия противоречащих случаев Схема рассуждения Элемент х1 имеет свойство Р. Элемент х2 имеет свойство Р. Элемент х3 имеет свойство Р. …. …. . Элемент хk имеет свойство Р. Все элементы х принадлежат классу М, который включает больше, чем k элементов. _____________ Вероятно, что все элементы х, принадлежащие классу М, имеют свойство Р

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ НЕПОЛНАЯ ИНДУКЦИЯ Типичные ошибки популярной индукции Правила, позволяющие минимизировать число ошибок популярной индукции - «поспешное обобщение» • - «после этого, значит по причине этого» • - «от сказанного с условием к сказанному безусловно» • • Число случаев, зарегистрированных в посылках, должно быть возможно большим. Случаи, на основе которых строится вывод, должны быть как можно разнообразнее. Рассматриваемые случаи должны быть типичными для всего исследуемого класса Если нет полной уверенности в истинности общего следствия, используйте частное суждение

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ НАУЧНАЯ ИНДУКЦИЯ Научная индукция – это неполная индукция, где заключение о принадлежности или не принадлежности некоторого признака каждому элементу данного множества делается на основе установления принадлежности (не принадлежности) этого признака лишь некоторой части элементов исследуемого множества с помощью каких-либо специальных (научных) методов Индукция через отбор разновидность научной индукции, при которой общее заключение получают на основании изучения особым образом отобранных некоторых элементов класса Индукция на основе причинно-следственной связи разновидность научной индукции, в которой общее заключение получают на основе установления необходимой (причинной) связи или необходимых признаков части предметов класса
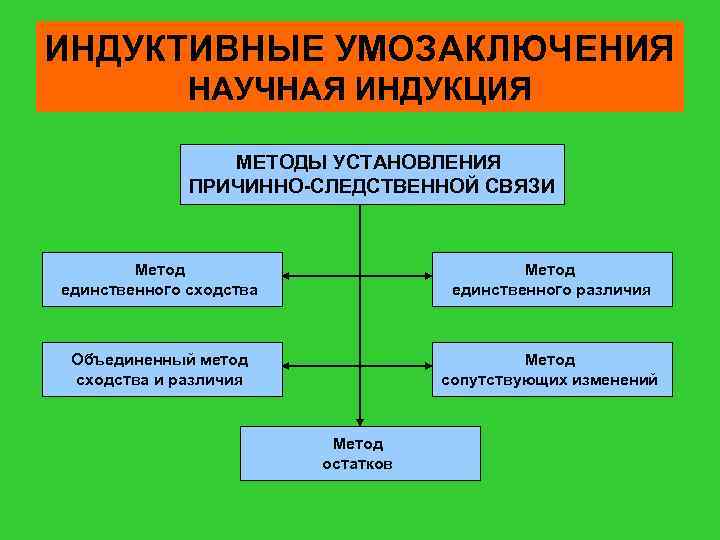
ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ НАУЧНАЯ ИНДУКЦИЯ МЕТОДЫ УСТАНОВЛЕНИЯ ПРИЧИННО-СЛЕДСТВЕННОЙ СВЯЗИ Метод единственного сходства Метод единственного различия Объединенный метод сходства и различия Метод cопутствующих изменений Метод остатков

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ МЕТОДЫ УСТАНОВЛЕНИЯ ПРИЧИННО-СЛЕДСТВЕННОЙ СВЯЗИ Метод единственного сходства: если какое–либо обстоятельство во всех случаях предшествует возникновению наблюдаемого явления, в то время, как другие обстоятельства изменяются, то, вероятно, именно это обстоятельство и является причиной возникновения наблюдаемого явления Схема рассуждения Условия ABCD - явление a Условия ACNK – явление a Условия ARHQ – явление a Вероятно, что A есть причина явления a

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ МЕТОДЫ УСТАНОВЛЕНИЯ ПРИЧИННО-СЛЕДСТВЕННОЙ СВЯЗИ Метод единственного различия: если установлено, что некоторое обстоятельство имеет место при возникновении наблюдаемого явления, но отсутствует, когда явление, за которым ведется наблюдение, не возникает, то делается вывод о том, что это обстоятельство, возможно, является причиной возникновения наблюдаемого явления Схема рассуждения Обстоятельства ABC не приводят к возникновению явления а Обстоятельства ABCD приводят к возникновению явления a Вероятно, что обстоятельство D является причиной возникновения явления а

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ МЕТОДЫ УСТАНОВЛЕНИЯ ПРИЧИННО-СЛЕДСТВЕННОЙ СВЯЗИ Метод объединенного сходства и различия представляет собой синтез методов единственного сходства и единственного различия Условия ABC-возникает a Условия BCD – явление не возникает Условия ANKL – возникает a Условия NKLR – явление не возникает Вероятно, что обстоятельство A есть причина явления а

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ МЕТОДЫ УСТАНОВЛЕНИЯ ПРИЧИННО-СЛЕДСТВЕННОЙ СВЯЗИ Метод сопутствующих изменений Если изменение предшествующего обстоятельства ведет к изменению наблюдаемого явления, при неизменности остальных предшествующих обстоятельств, то, возможно, что именно это обстоятельство и является причиной возникновения наблюдаемого явления Схема рассуждения При обстоятельствах А 1 ВС наблюдается явление а 1. При обстоятельствах А 2 ВС наблюдается явление а 2. При обстоятельствах А 3 ВС наблюдается явление а 3. ___________ Вероятно, что А есть причина а.

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ МЕТОДЫ УСТАНОВЛЕНИЯ ПРИЧИННО-СЛЕДСТВЕННОЙ СВЯЗИ Метод остатков если изучаемому сложному явлению abcde предшествуют обстоятельства ABCDE, из которых A есть причина а, B - причина b, C - причина c, а D является причиной d , то можно предположить, что причиной е является обстоятельство Е Схема рассуждения Обстоятельства ABCDE соответствуют сложному явлению abcde. Известно, что A есть причина a, B – причина b, C – причина c, D вызывает d. Вероятно, что обстоятельство E является причиной e.
НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ АНАЛОГИЯ Умозаключение по аналогии или аналогия – недедуктивное умозаключение, в котором на основе сходства двух объектов по каким-либо параметрам делается вывод об их сходстве по другим параметрам АНАЛОГИЯ СВОЙСТВ АНАЛОГИЯ ОТНОШЕНИЙ

НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ АНАЛОГИЯ Аналогия свойств – умозаключение по аналогии, в котором сравниваются два различных предмета, и на основе установления общности их некоторых свойств, свойство, присущее одному из этих предметов, переносится на другой предмет. Схема рассуждения Предмет А имеет свойства PQRL. Предмет В имеет свойства PQRLM. Вероятно, что предмет А имеет свойство M.

НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ АНАЛОГИЯ Аналогия отношений - Схема рассуждения умозаключение по аналогии, в котором сравниваются отношения между предметами, и на основе общности их некоторых свойств, свойство, присущее одному отношению переносится на другое отношение Между предметами A и B имеется отношение R. Между предметами C и D имеется отношение P. Отношение R обладает свойствами FIKQ. Отношение P обладает свойствами FIK. Возможно, что отношение P обладает свойством Q.
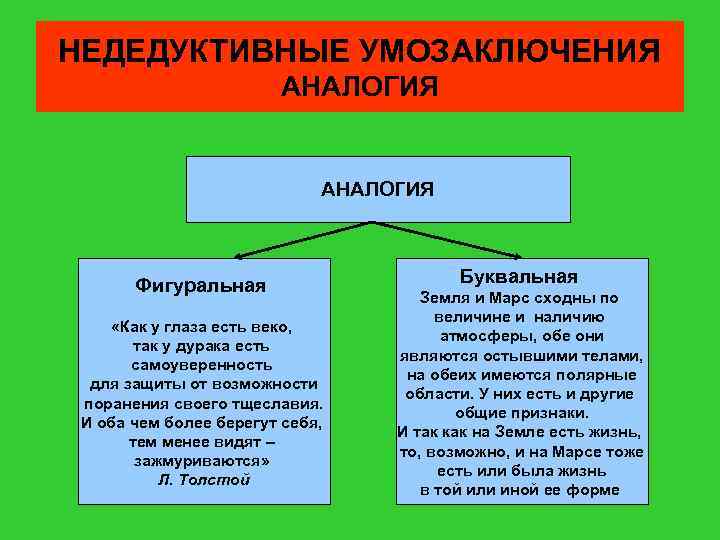
НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ АНАЛОГИЯ Фигуральная «Как у глаза есть веко, так у дурака есть самоуверенность для защиты от возможности поранения своего тщеславия. И оба чем более берегут себя, тем менее видят – зажмуриваются» Л. Толстой Буквальная Земля и Марс сходны по величине и наличию атмосферы, обе они являются остывшими телами, на обеих имеются полярные области. У них есть и другие общие признаки. И так как на Земле есть жизнь, то, возможно, и на Марсе тоже есть или была жизнь в той или иной ее форме
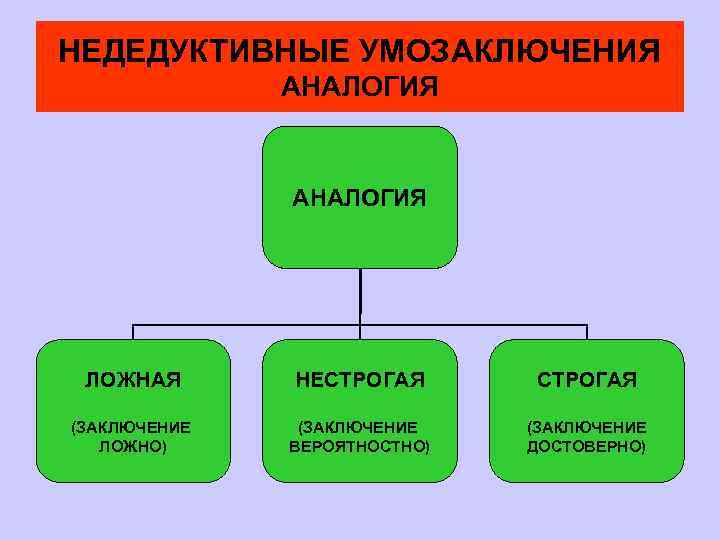
НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ АНАЛОГИЯ ЛОЖНАЯ НЕСТРОГАЯ (ЗАКЛЮЧЕНИЕ ЛОЖНО) (ЗАКЛЮЧЕНИЕ ВЕРОЯТНОСТНО) (ЗАКЛЮЧЕНИЕ ДОСТОВЕРНО)

НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ АНАЛОГИЯ СТРОГАЯ АНАЛОГИЯ (схема рассуждения) • Объект А обладает признаками PQRL. • Объект В обладает признаками PQL. • Из наличия признаков PQL необходимо следует наличие признака R. ___________________ • Достоверно, что объект В обладает признаком R.

НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ АНАЛОГИЯ Условия, повышающие степень вероятности заключений по аналогии • • • У сравниваемых объектов должно быть как можно больше общих признаков; Эти общие признаки должны быть существенными, а по возможности отличительными; Общие признаки должны быть как можно более разнородными: они должны охватывать разные стороны сравниваемых предметов; Сравниваемые признаки должны быть одного и того же типа, что переносимый признак, и тесно связанными с ним. Сравниваемые объекты должны иметь как можно меньше различий
НЕДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ АНАЛОГИЯ Модель Реальная Идеальная (физическая, ситуационная и т. п. ) (математическая, компьютерная и т. п. )

Тема V. ОСНОВЫ ТЕОРИИ Тема АРГУМЕНТАЦИИ V. 1. Общая характеристика аргументации. Виды аргументации. V. 2. Виды доказательства. V. 3. Способы опровержения. V. 4. Правила доказательства и опровержения. Ошибки, возникающие в доказательствах и опровержениях. V. 5. Паралогизмы. Софизмы и парадоксы.
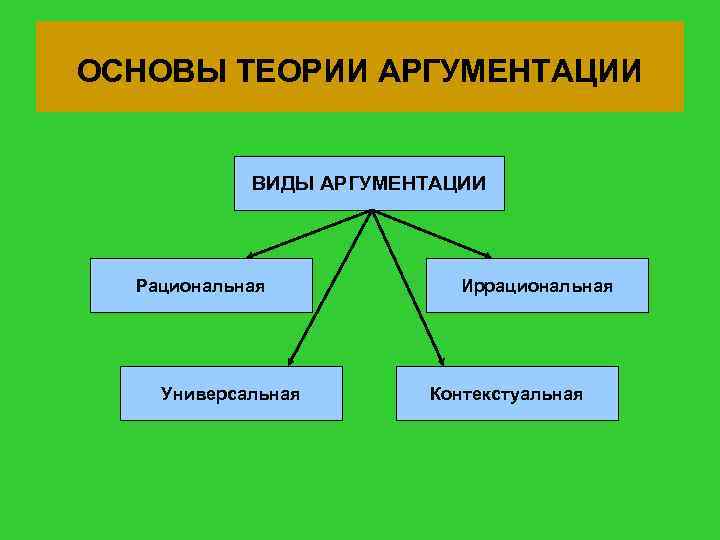
ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ВИДЫ АРГУМЕНТАЦИИ Рациональная Универсальная Иррациональная Контекстуальная
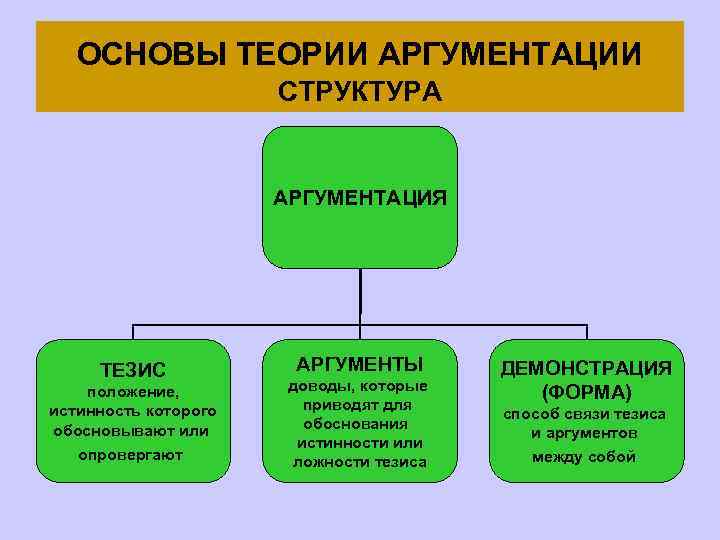
ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ СТРУКТУРА АРГУМЕНТАЦИЯ ТЕЗИС положение, истинность которого обосновывают или опровергают АРГУМЕНТЫ доводы, которые приводят для обоснования истинности или ложности тезиса ДЕМОНСТРАЦИЯ (ФОРМА) способ связи тезиса и аргументов между собой

ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ СТРУКТУРА Общий вид (a 1, a 2, a 3, … ak) T где a 1, a 2, a 3, … ak – аргументы, T – тезис
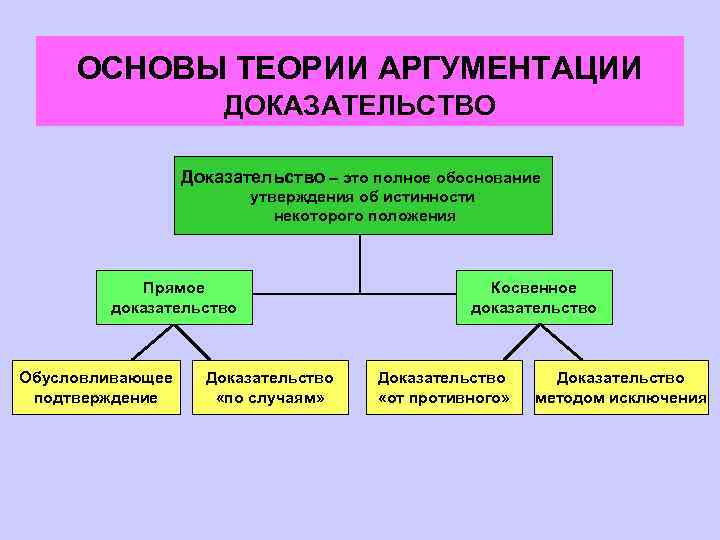
ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ Логика классов ДОКАЗАТЕЛЬСТВО Доказательство – это полное обоснование утверждения об истинности некоторого положения Прямое доказательство Обусловливающее подтверждение Доказательство «по случаям» Косвенное доказательство Доказательство «от противного» Доказательство методом исключения

ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ДОКАЗАТЕЛЬСТВО Способы прямого доказательства Обусловливающее подтверждение тезиса ( A, B, C, D ) → T, A, B, C, D T Соединительное подтверждение тезиса а) Ти; б) Ти; в) Ти. а), б), в) – все частные случаи М. Ти в М.

ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ДОКАЗАТЕЛЬСТВО Способы косвенного доказательства Доказательство «от противного» T v ~ Т, ~ Т → (аΛ ~а) Разделительное подтверждение тезиса A / B / C / T, ~A, ~B, ~C ~ Т- ложен T - истинен Т
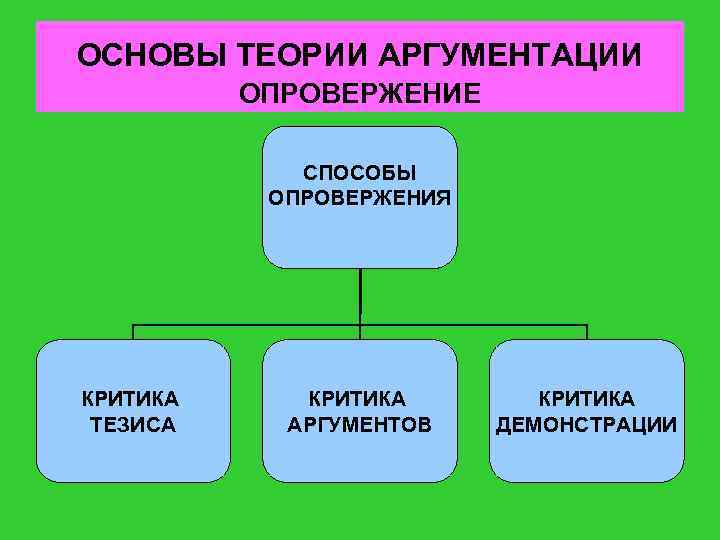
ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ОПРОВЕРЖЕНИЕ СПОСОБЫ ОПРОВЕРЖЕНИЯ КРИТИКА ТЕЗИСА КРИТИКА АРГУМЕНТОВ КРИТИКА ДЕМОНСТРАЦИИ
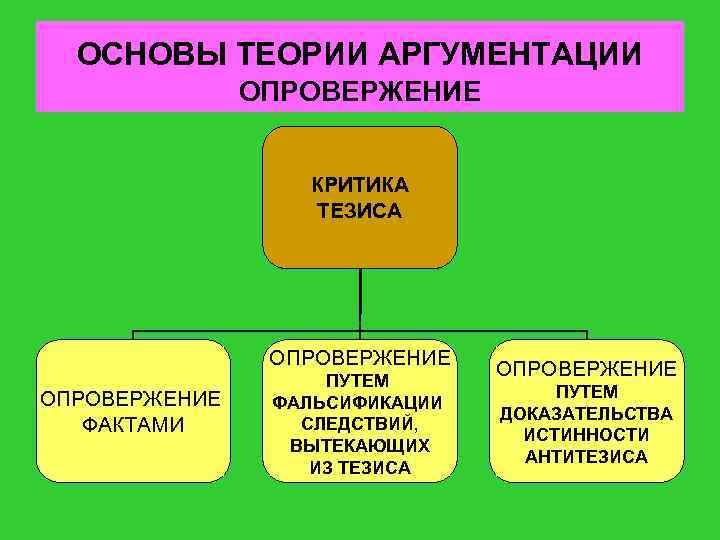
ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ОПРОВЕРЖЕНИЕ КРИТИКА ТЕЗИСА ОПРОВЕРЖЕНИЕ ФАКТАМИ ПУТЕМ ФАЛЬСИФИКАЦИИ СЛЕДСТВИЙ, ВЫТЕКАЮЩИХ ИЗ ТЕЗИСА ОПРОВЕРЖЕНИЕ ПУТЕМ ДОКАЗАТЕЛЬСТВА ИСТИННОСТИ АНТИТЕЗИСА
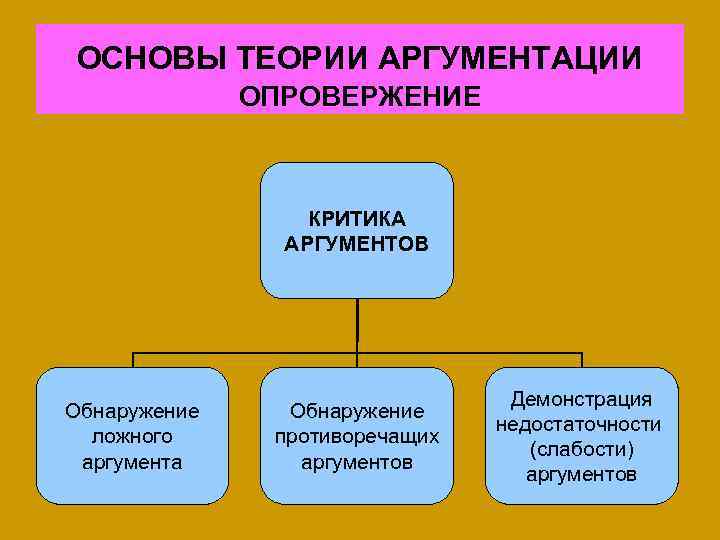
ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ОПРОВЕРЖЕНИЕ КРИТИКА АРГУМЕНТОВ Обнаружение ложного аргумента Обнаружение противоречащих аргументов Демонстрация недостаточности (слабости) аргументов

ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ПРАВИЛА ДОКАЗАТЕЛЬСТВА И ОПРОВЕРЖЕНИЯ По отношению к тезису 1. Тезис должен быть четким и ясным. 2. Тезис должен оставаться неизменным на всем протяжении рассуждения. По отношению к аргументам 1. Аргументы должны быть истинными положениями. 2. Истинность аргументов должна быть установлена независимо от истинности тезиса. 3. Аргументы не должны противоречить другу. 4. Аргументы должны быть достаточными для доказательства (опровержения) данного тезиса. По отношению к демонстрации Доказательство и опровержение должны строиться с учетом правил умозаключений, которым они соответствуют

ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ОШИБКИ ДОКАЗАТЕЛЬСТВА И ОПРОВЕРЖЕНИЯ По отношению к тезису 1. Нечеткий, «размытый» или неясный тезис 2. Потеря тезиса. 3. Подмена тезиса 4. «Переход в другой род» . 5. Довод к человеку По отношению к аргументам 1. «Основное заблуждение» или «ложное основание» 2. «Предвосхищение основания» 3. «Круг в доказательстве» 4. Выдвижение аргументов, противоречащих другу 5. «Слабость» , Недостаточность аргументов По отношению к демонстрации 1. «Мнимое следование» 2. «От сказанного с условием, к сказанному безусловно» 3. Нарушение правил умозаключений, лежащих в основе аргументации.

ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ ПАРАЛОГИЗМЫ, СОФИЗМЫ И ПАРАДОКСЫ Паралогизм - неумышленная логическая ошибка в рассуждениях Софизм – умышленная логическая ошибка. Пример софизма: «То, что ты не терял, ты имеешь. Ты не терял рогов. Значит, у тебя есть рога» Парадокс - в логике это: 1. логическое противоречие, неразрешимое с точки зрения здравого смысла или общепринятых научных представлений 2. интуитивно убедительное рассуждение, приводящее к противоречию Пример: парадокс «Лжец» «Лжет ли тот, кто говорит, что он лжет? »

Тема VI. ГИПОТЕЗА VI. 1. Понятие гипотезы. Виды гипотез. VI. 2. Подтверждение гипотез. VI. 3. Опровержение гипотез.
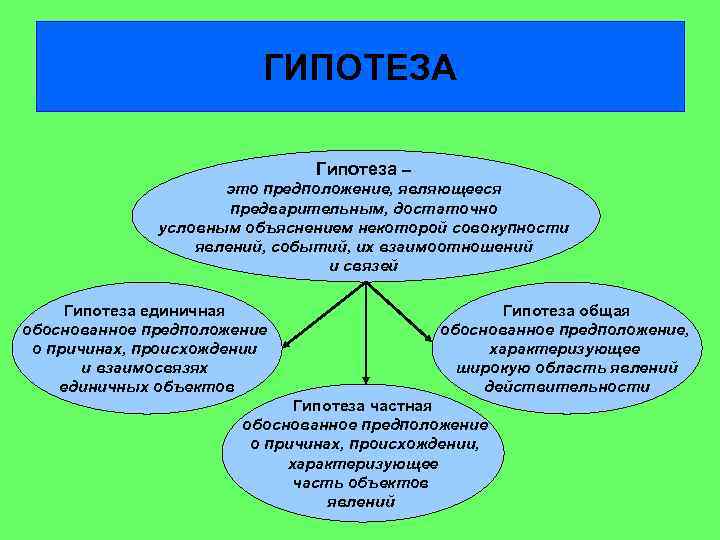
ГИПОТЕЗА Гипотеза – это предположение, являющееся предварительным, достаточно условным объяснением некоторой совокупности явлений, событий, их взаимоотношений и связей Гипотеза единичная обоснованное предположение о причинах, происхождении и взаимосвязях единичных объектов Гипотеза общая обоснованное предположение, характеризующее широкую область явлений действительности Гипотеза частная обоснованное предположение о причинах, происхождении, характеризующее часть объектов явлений
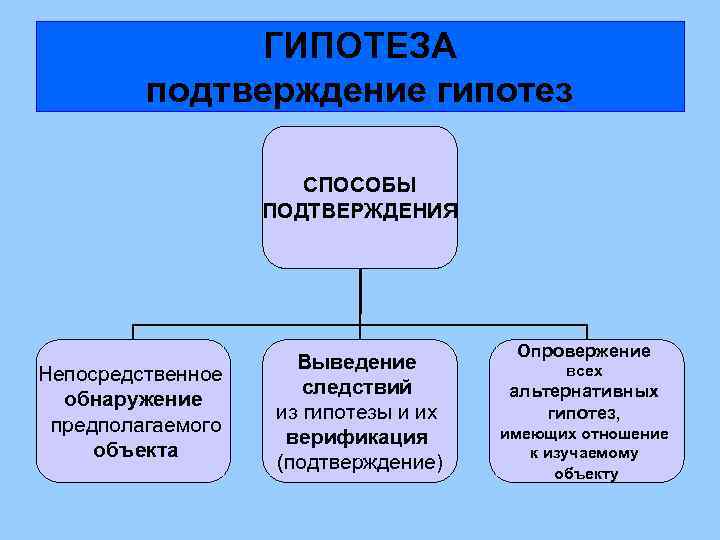
ГИПОТЕЗА подтверждение гипотез СПОСОБЫ ПОДТВЕРЖДЕНИЯ Непосредственное обнаружение предполагаемого объекта Выведение следствий из гипотезы и их верификация (подтверждение) Опровержение всех альтернативных гипотез, имеющих отношение к изучаемому объекту
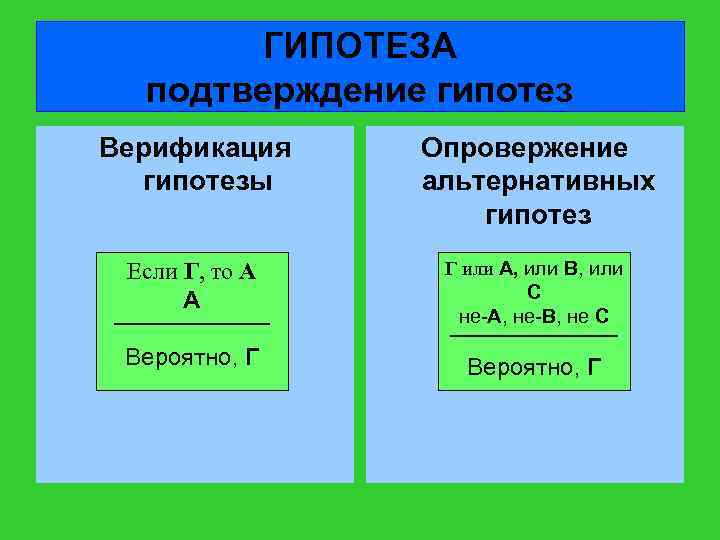
ГИПОТЕЗА подтверждение гипотез Верификация гипотезы Опровержение альтернативных гипотез Если Г, то А А Г или А, или В, или С не-А, не-В, не С Вероятно, Г
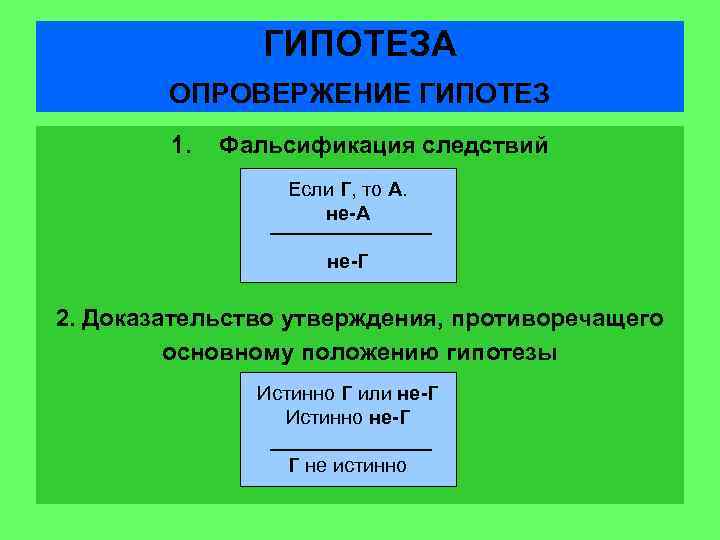
ГИПОТЕЗА ОПРОВЕРЖЕНИЕ ГИПОТЕЗ 1. Фальсификация следствий Если Г, то А. не-А не-Г 2. Доказательство утверждения, противоречащего основному положению гипотезы Истинно Г или не-Г Истинно не-Г Г не истинно