Логические основы ЭВМ Выполнила студентка II курса 14

Логические основы ЭВМ Выполнила студентка II курса, 14 группы стоматологического факультета НГМУ Кулешова Александра

• В 1854 г. Джон Буль положил начало математической логике. Около 30 лет назад оформилась в самостоятельную дисциплину. • Математическая логика изучает только рассуждения со строго определенными объектами и суждениями, для которых возможно однозначно решить «истины» они, или «ложны» . Большинство устройств ЭВМ состоит из компонентов с двумя устойчивыми состояниями и их удобно описывать на наборе логических функций принимающих значения { 0; 1 }. • Логические функции характеризуются таблицами истинности.

Инверсия (логическое отрицание) _ f (x) = x Соответствующие выражения языка: • Не «х» • Неверно, что «х»

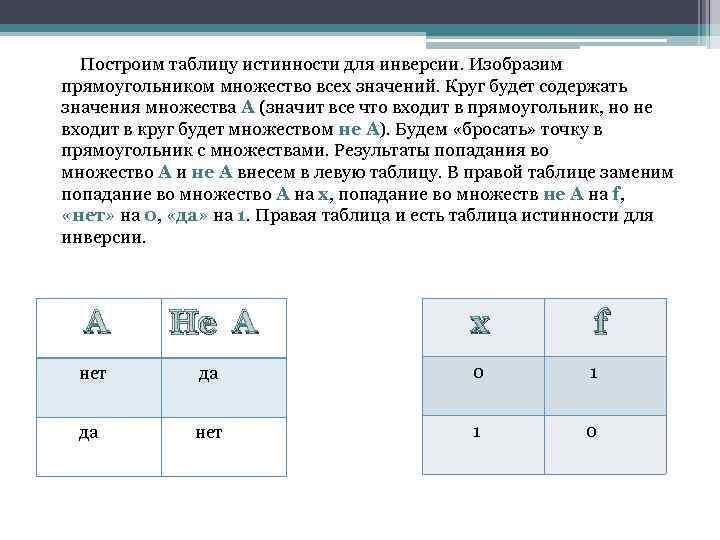Построим таблицу истинности для инверсии. Изобразим прямоугольником множество всех значений. Круг будет содержать значения множества А (значит все что входит в прямоугольник, но не входит в круг будет множеством не А). Будем «бросать» точку в прямоугольник с множествами. Результаты попадания во множество А и не А внесем в левую таблицу. В правой таблице заменим попадание во множество А на х, попадание во множеств не А на f, «нет» на 0, «да» на 1. Правая таблица и есть таблица истинности для инверсии. А Не А х f нет да 0 1 да нет 1 0

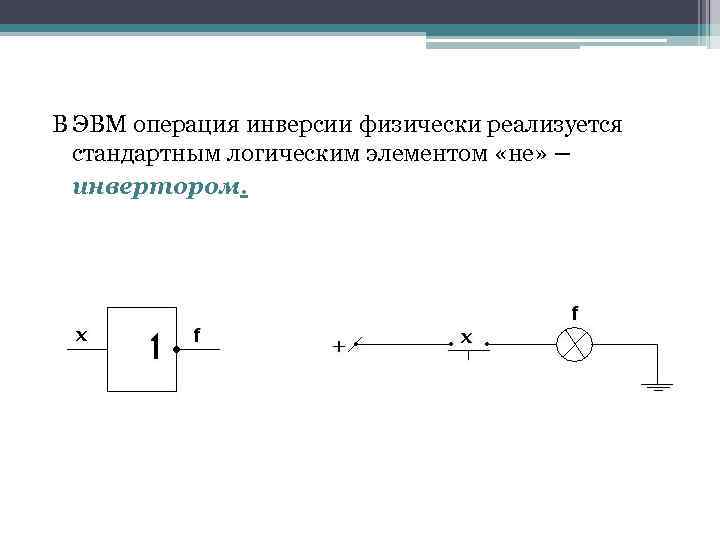В ЭВМ операция инверсии физически реализуется стандартным логическим элементом «не» – инвертором.

Дизъюнкция (логическое сложение). f (x, у) = x Ú у Соответствующие выражения языка: • Х или Y или оба

Построим таблицу истинности для дизъюнкции. Изобразим прямоугольником множество всех значений. Первый круг будет содержать значения множества А, второй круг значения множества В. Множеством А или В будет объединение этих кругов (на рисунке закрашена серым цветом). Будем «бросать» точку в прямоугольник с множествами. Результаты попадания во множество А, В и А или В внесем в левую таблицу. В правой таблице заменим попадание во множество А на х, В на у, попадание во множество А или В на f, «нет» на 0, «да» на 1. Правая таблица и есть таблица истинности для дизъюнкции.