Логические цепи И конъюнктор ИЛИ дизъюнктор

Логические цепи «И» – конъюнктор «ИЛИ» – дизъюнктор «НЕ» – инвертор II. Рис. 1. Элементы «И» , «ИЛИ» , «НЕ»

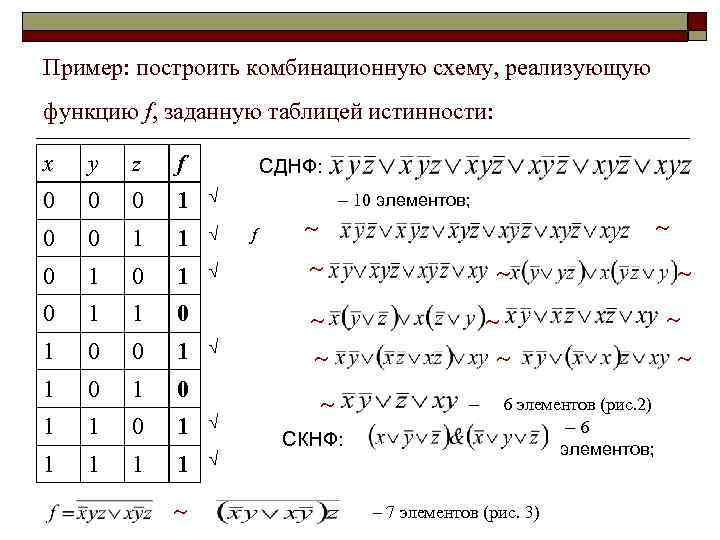Пример: построить комбинационную схему, реализующую функцию f, заданную таблицей истинности: x y z f 0 0 0 1 1 0 1 0 1 0 0 1 1 1 CДНФ: – 10 элементов; f СКНФ: – 6 элементов (рис. 2) – 6 элементов; – 7 элементов (рис. 3)

Исчисление высказываний (ИВ) I. III. IV. V. VI. План построения формальных теорий: задается алфавит; дается определение формулы; некоторые из формул объявляются аксиомами; формулируются правила вывода; дается определение вывода формулы (формального доказательства); дается определение выводимой формулы (теоремы).

Построение исчисления высказываний 1. 2. 3. I. Алфавит : x, y, …, z, . . . , А, В, … – пропозициональные переменные; , – логические связки; (, ) – технические символы.

II. Определение формулы исчисления высказываний (п. п. ф. ): 1) 2) 3) 4) каждая пропозициональная переменная является п. п. ф. ; если А – п. п. ф. (ИВ), то ( А) – п. п. ф. (ИВ); если А и В – п. п. формулы (ИВ), то (А В) – тоже п. п. формула (ИВ); никаких других п. п. ф. (ИВ), кроме получающихся согласно п. п. 1– 3, нет.

III. Аксиомы (А 1): А (В А); (А 2): А (В С) ((А В) (А С)) – закон самодистрибутивности импликации; (А 3): – закон контрапозиции.

Пример: (А 1): А (В А); (А 1): (x y) (( (z x)) (x y)) – сделаны замены А=(x y), В= (z x).

IV. Правило вывода (modus ponens) (MP):

V. Вывод формулы А (формальное доказательство) VI. ├ А ИСЧИСЛЕНИЕ содержит выводимые формулы (теоремы)

Примеры выводимых формул 1. ├ А А ├x A (y z) ((B A) A) A 1 ((x y) (x z)) ((A (B A)) (A A)) A 1 (A 2)

1. ├ А А 1)├A ((B A) A) ((A (B A)) (A A)) …. . . …(A 2) A 1 2)├A ((B A) A)…………………. . (A 1) 3)├(A (B A)) (A A)………………. . из 1), 2) по (MP) 2) – малая посылка, 1) – большая посылка 4)├A (B A)………………………. (A 1) 5)├A A…………………………. . из 3), 4) по (MP) 4) – малая посылка, 3) – большая посылка

(А B) 2. ├ ├x (y (( z) ((x y) ) (A B)) (( ( А 3 (x )) ( А 1 z)) (A B))) (A 2)

2. ├ (А B) 1)├ (A 2) 2)├ ………………………. (A 3) 3)├ (A 1) 4)├ 3) по (MP) ………………. из 2) 5)├ 4) по (MP) ……………. . . из 1),

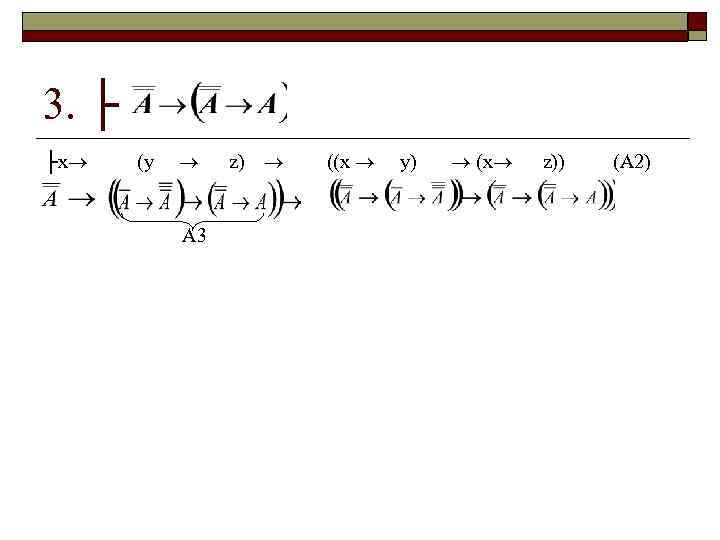3. ├ ├x (y А 3 z) ((x y) (x z)) (A 2)

3. ├ ├x 1)├ (y ((x y) (x z)) (A 2) …………. (A 2) 2)├ 3)├ z) ……………. . . (A 3) (A 1) 4)├ ………………. . . из 2), 3) по (MP) 5)├ ……………. . . из 1), 4) по (MP) 6)├ ………. . . ………………………. …. (2 пример – 7 формул) 7)├ ………………………. . из 5), 6) по (MP)

4. ├ ├x (y z) ((x y) (x z)) (A 2)

4. ├ 1)├ …………………(А 2) 2)├ ………………… 3 пример – 13 формул 3)├ . . . …. ………………. . . из 1), 2) по (MP) 4)├ . . . ……………………. . 1 пример – 5 формул 5)├ ………………………. . из 3), 4) по (MP)

5. ├ ├ (А 3) 1)├ ………………………. . (А 3) 2)├ ……………………. 4 пример – 21 формула 3)├ ……………………… из 1), 2) по (MP)

Вывод формул из гипотез Опр. Выводом формулы А из множества гипотез Г называется конечная последовательность формул F 1, F 2, …, Fk, заканчивающаяся формулой А (Fk=A) и каждая формула в этой последовательности является или аксиомой, или гипотезой, или получена из двух предыдущих по правилу (MP). Обозн. Г├ А (из Г выводима А)

Пример: построить вывод формулы С из гипотез: А, А В, В С. 1) А гип. 1; 2) А В гип. 2; 3) В С гип. 3; 4) В (МР) к 1), 2) 5) С (МР) к 3), 4).

Свойства вывода формул из гипотез. 1. Г, А├А (свойство самовыводимости). 2. Если Г├А, то Г, В├А, где В – любая формула (расширение списка гипотез). 3. Г, В├А и Г├В, то Г├А (выводимые гипотезы можно исключать из списка гипотез, при этом выводимость данной формулы не нарушается).

Свойства вывода формул из гипотез. 4. Если из Г├А и А├В, то Г├В ( свойство транзитивности вывода). 5. Если из Г, А, А├В, то Г, А├В (свойство сокращения). 6. Если из Г, А, В├С, то Г, В, А├С (свойство коммутативности).

Теорема дедукции Т. Если Г, А├В, то Г├А В. Г, А├В Г├А В Дано: вывод формулы В из Г, А. : (1) F 1, F 2, …, Fn=B. Доказать: формула А В выводима из множества гипотез Г. Доказательство: (2) А F 1, А F 2, …, А Fn=А B.