Логические

Логические основы ЭВМ Высказывание – повествовательное предложение, о котором можно сказать, истинно оно или ложно. Высказывания могут принимать одно из двух значений: ЛОЖЬ или ИСТИНА Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности (А = В).

Сложное высказывание можно построить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логических операций.

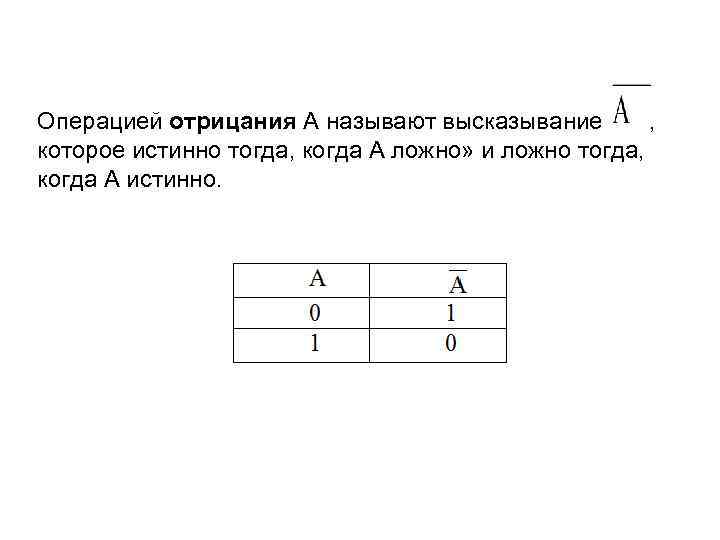
Операцией отрицания А называют высказывание , которое истинно тогда, когда А ложно» и ложно тогда, когда А истинно.

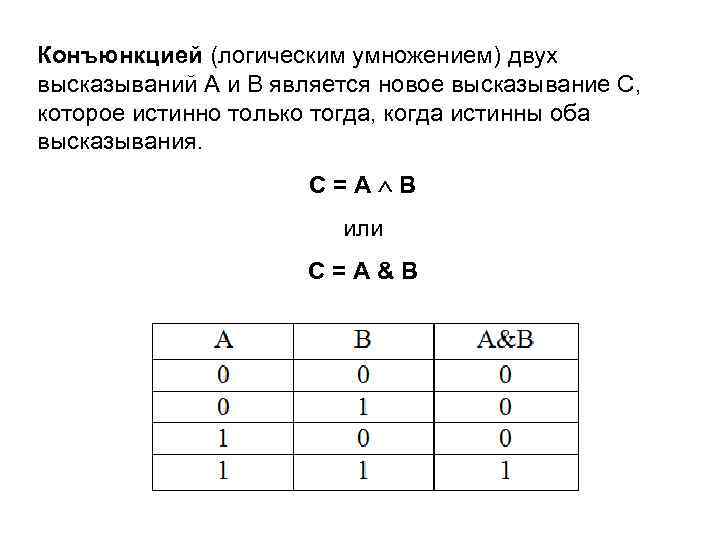
Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания. С=А В или С=А&В

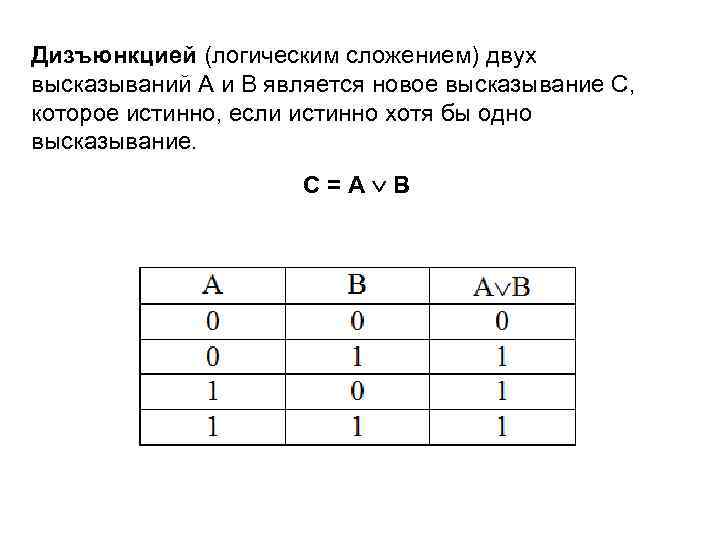
Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. С=A В

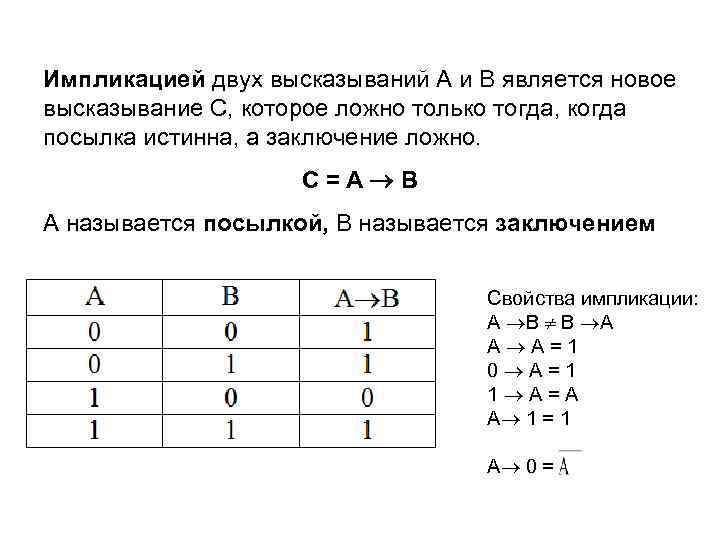
Импликацией двух высказываний А и В является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно. С=А В А называется посылкой, В называется заключением Свойства импликации: А В В А А А=1 0 А=1 1 А=А А 1 = 1 А 0 =

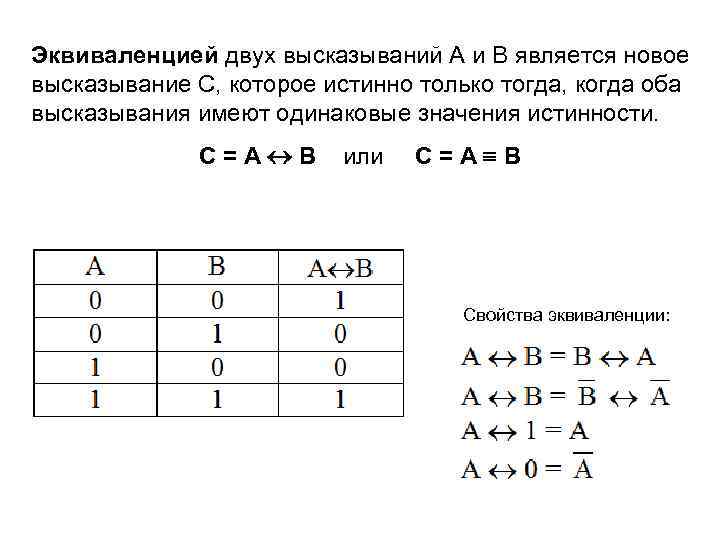
Эквиваленцией двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда оба высказывания имеют одинаковые значения истинности. С=А В или С=А В Свойства эквиваленции:

С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические выражения. Соглашение о старшинстве операций: первыми выполняются операции в скобках, затем отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция. Операции не являются независимыми, одни из них могут быть выражены через другие.

1. Закон двойного отрицания 2. Коммутативный закон для конъюнкции 3. Коммутативный закон для дизъюнкции 4. Ассоциативный закон для конъюнкции 5. Ассоциативный закон для дизъюнкции 6. Дистрибутивные законы 7. Законы де Моргана 8. Закон идемпотенции для конъюнкции 9. Закон идемпотенции для дизъюнкции

10. Закон единицы для конъюнкции 11. Закон нуля для конъюнкции 12. Закон единицы для дизъюнкции 13. Закон нуля дизъюнкции 14. Закон исключения третьего 15. Закон противоречия 16. Законы поглощения

Дизъюнктивная нормальная форма (ДНФ) A 1 А 2 . . . Аn, где каждое из составляющих высказываний есть конъюнкция простых высказываний и их отрицаний. Конъюнктивная нормальная форма (КНФ) А 1 А 2 . . . Аn, где каждое из составляющих есть дизъюнкция простых высказываний и их отрицаний.

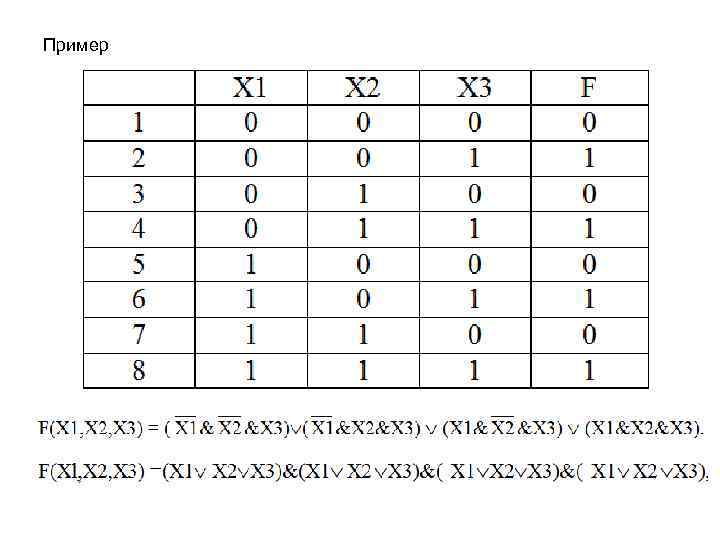
Пример

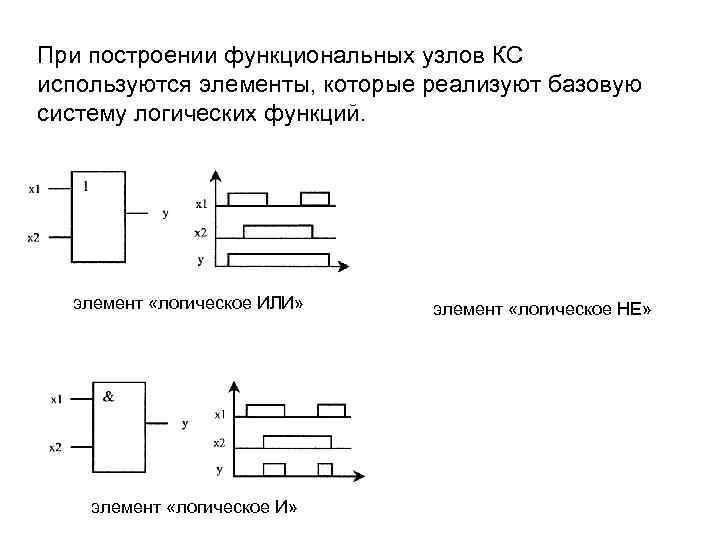
При построении функциональных узлов КС используются элементы, которые реализуют базовую систему логических функций. элемент «логическое ИЛИ» элемент «логическое НЕ» элемент «логическое И»

Функциональное устройство, которое может по команде принять или выдать один двоичный бит и сохранять его сколь угодно долго называется триггер Условное обозначение триггера

Схема триггера в состоянии Запись в триггер единицы хранения бита информации

Функциональные узлы, способные хранить двоичные числа, осуществлять их синхронную параллельную передачу и запись, а также выполнять с ними некоторые специальные операции называются регистрами. n-разрядный регистр хранения с синхронной записью и чтением