Логическая информация и основы логики Алгебра логики

Логическая информация и основы логики.

Алгебра логики это наука – об общих операциях, которые могут выполняться над логическими выражениями. Логическое выражение – это простое или сложное высказывание.

В алгебре высказываний высказывания обозначаются именами логических переменных (заглавные буквы латинского алфавита), которые могут принимать лишь два значения «истинно» и «ложно» . Высказывание истинное = 1 Высказывание ложное = 0

«Два умножить на два равно четырем» истинное высказывание. A=1 «Два умножить на два равно пяти» ложное высказывание. B=0

В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания. Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «И» , «ИЛИ» , «НЕ» .

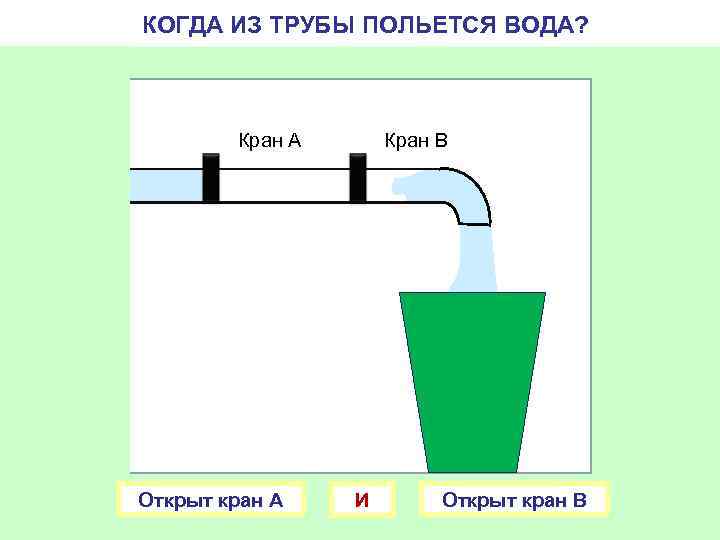
КОГДА ИЗ ТРУБЫ ПОЛЬЕТСЯ ВОДА? Кран А Открыт кран А Кран В И Открыт кран В

Конъюнкция Объединение двух или нескольких высказываний в одн с помощью союза «И»

Конъюнкция (conjunctio «связываю» ) – Русский язык союзы А, НО, ХОТЯ – И, Математическая логиказнак – или Иное название логическое умножение – Вид записи - &

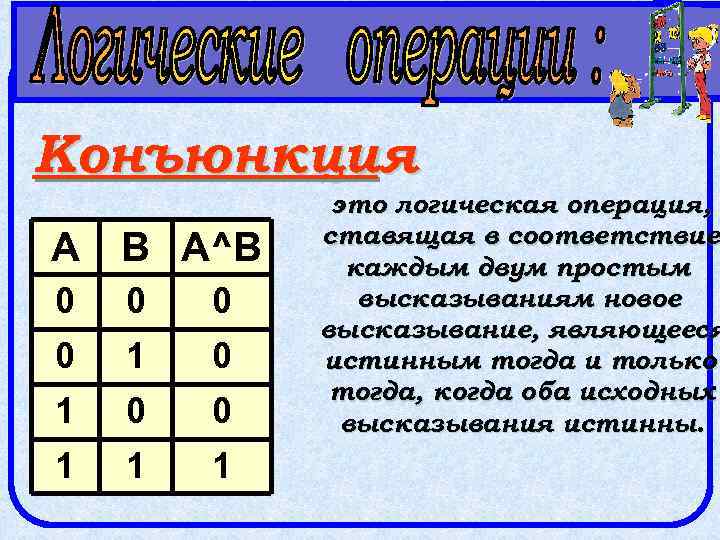
Конъюнкция А В А^В 0 0 1 1 1 это логическая операция, ставящая в соответствие каждым двум простым высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Пример: Число 6 делится на 2 и на 3 Число 6 делится на 2 и на 4 Число 6 6 делится на 2 (истина) делится на 8 и на 3 А: Число 6 делится на 5 и на 9 Число 6 делится на 2 (истина) А: Число 6 делится 3 8 (ложь) В: Число 6 делится на на(истина) А: Число 6 делится (ложь) В: Число 6 делится на на 5 (ложь) 4 В: Число 6 делится на 3 (истина) В: F: A ^ B = 1 ^на 3= 1 Число 6 делится 1 (ложь) FF: A^^B ==1 ^01 = 0 : A =0 B = 0^^ 0 = 0 0 F: A ^ B

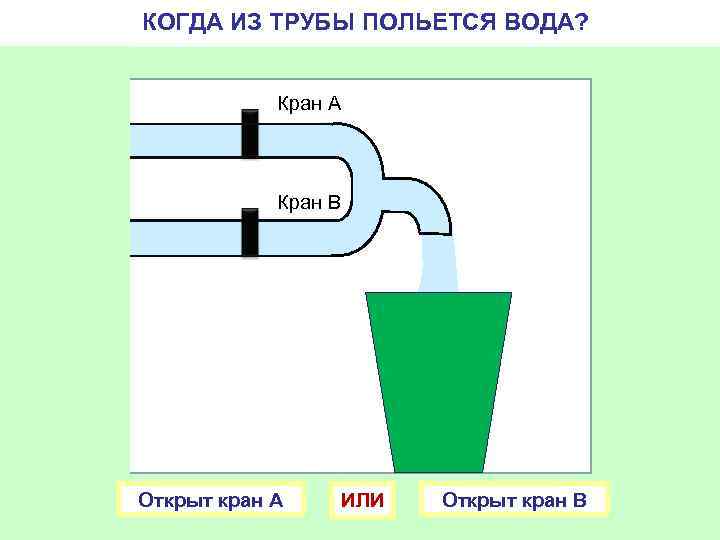
КОГДА ИЗ ТРУБЫ ПОЛЬЕТСЯ ВОДА? Кран А Кран В Открыт кран А ИЛИ Открыт кран В

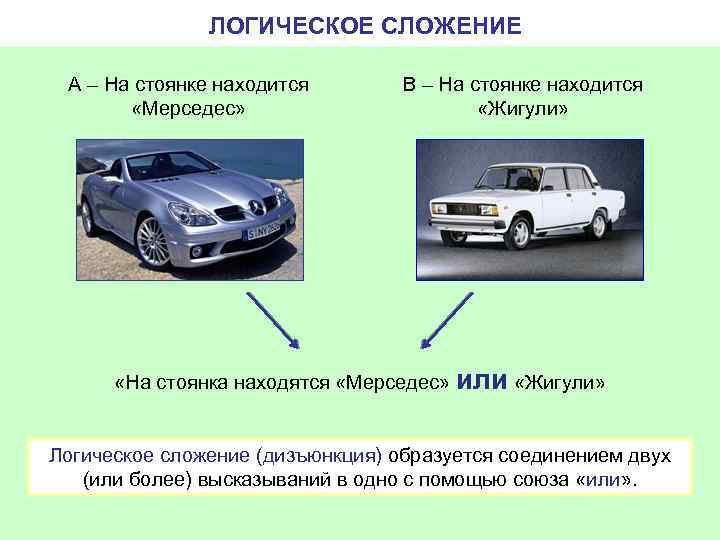
ЛОГИЧЕСКОЕ СЛОЖЕНИЕ А – На стоянке находится «Мерседес» В – На стоянке находится «Жигули» «На стоянка находятся «Мерседес» или «Жигули» Логическое сложение (дизъюнкция) образуется соединением двух (или более) высказываний в одно с помощью союза «или» .

Дизъюнкция Объединение двух или нескольких высказываний в одн с помощью союза «ИЛИ»

Дизъюнкция (disjunctio «различаю» ) – Русский язык союзы – ИЛИ Математическая логиказнак – Иное название логическое сложение – Вид записи -

Дизъюнкция А В Аv. В 0 0 1 1 1 0 1 1 это логическая операция, ставящая в соответствие каждым двум простым высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда хотя бы одно из двух исходных высказываний истинно.

Пример: Число 6 делится на 2 или на 3 Число 6 делится на 2 или на 5 Число 6 6 делится на 2 (истина) 3 делится на 7 или на А: Число 6 делится на 4 или на 5 Число 6 делится на 2 (истина) А: Число 6 делится 3 7 (ложь) В: Число 6 делится на на(истина) А: Число 6 делится (ложь) В: Число 6 делится на на 4 (ложь) 5 В: Число 6 делится на 3 (истина) В: F: A v 6 B = 1 v 1 = (ложь) Число делится на 5 1 FF: Avv. B ==1 vv 01 = 1 : A =1 B =0 v 0=0 0 F: A v B

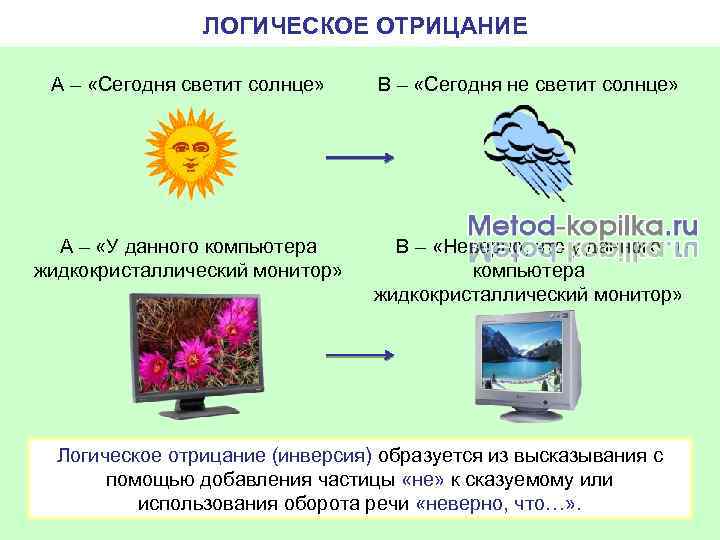
ЛОГИЧЕСКОЕ ОТРИЦАНИЕ А – «Сегодня светит солнце» В – «Сегодня не светит солнце» А – «У данного компьютера жидкокристаллический монитор» В – «Неверно, что у данного компьютера жидкокристаллический монитор» Логическое отрицание (инверсия) образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что…» .

Инверсия (inversio– «переворачиваю» ) Русский язык союзы – НЕ; НЕВЕРНО, ЧТО… Математическая логиказнак – или Иное название логическое отрицание – Вид записи - или

Инверсия Присоединение частицы «НЕ» к высказыванию.

Инверсия А 0 1 1 0 это логическая операция, которая каждому данному высказыванию ставит в соответствие новое высказывание, являющееся истинным тогда, когда данное высказывание ложно, и ложным, если данное высказывание истинно.

Пример: Число 32 делится на 2 Число 32 делится на 7 А: Число 32 делится на 2 (истина) А: Число 32 делится на 7 (ложь) не А: Число 32 не делится на 2 (ложь) не А: Число 32 не делится на 7 (истина) FF: ==1 = 01 : 0=

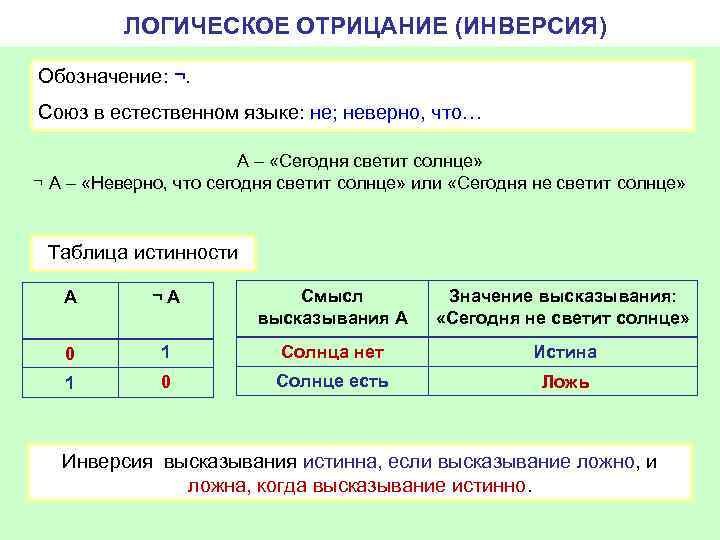
ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ) Обозначение: ¬. Союз в естественном языке: не; неверно, что… А – «Сегодня светит солнце» ¬ А – «Неверно, что сегодня светит солнце» или «Сегодня не светит солнце» Таблица истинности А ¬А Смысл высказывания А Значение высказывания: «Сегодня не светит солнце» 0 1 Солнца нет Истина 1 0 Солнце есть Ложь Инверсия высказывания истинна, если высказывание ложно, и ложна, когда высказывание истинно.

ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ Обозначение: →. Союз в естественном языке: если…, то…. Если на улице, то асфальт мокрый. Если хорошо горит красный свет на светофоре, то стою и жду зеленый. Если прямо пойдешь, то коня потеряешь. Если коровы летают, то дважды два – пять. Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…» .

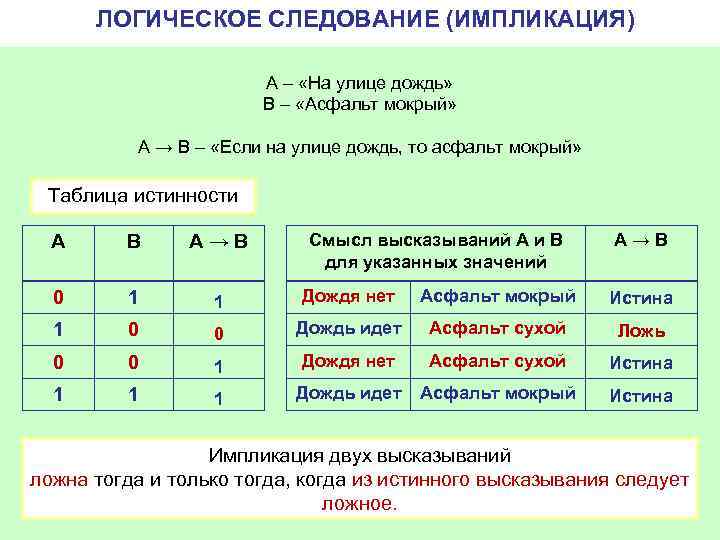
ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ (ИМПЛИКАЦИЯ) А – «На улице дождь» В – «Асфальт мокрый» А → B – «Если на улице дождь, то асфальт мокрый» Таблица истинности Смысл высказываний А и В для указанных значений А→B А В А→B 0 1 1 Дождя нет Асфальт мокрый Истина 1 0 0 Дождь идет Асфальт сухой Ложь 0 0 1 Дождя нет Асфальт сухой Истина 1 1 1 Дождь идет Асфальт мокрый Истина Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное.

Проверка домашнего задания • • • Понятие - это форма мышление, фиксирующая основные, существенные признаки объекта, которые отличают его от других объектов. Высказывание - это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними. Высказывание может быть либо истинно, либо ложно. Суждения – это некоторые высказывания,

ЛОГИЧЕСКОЕ РАВЕНСТВО Обозначение: =, ↔, ~. Союз в естественном языке: тогда и только тогда, когда…. Число А – четное, тогда и только тогда, когда число А делится нацело на 2. Прямоугольник является квадратом тогда и только тогда, когда все его стороны равны. Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно при помощи оборота речи «… тогда и только тогда, когда…» .

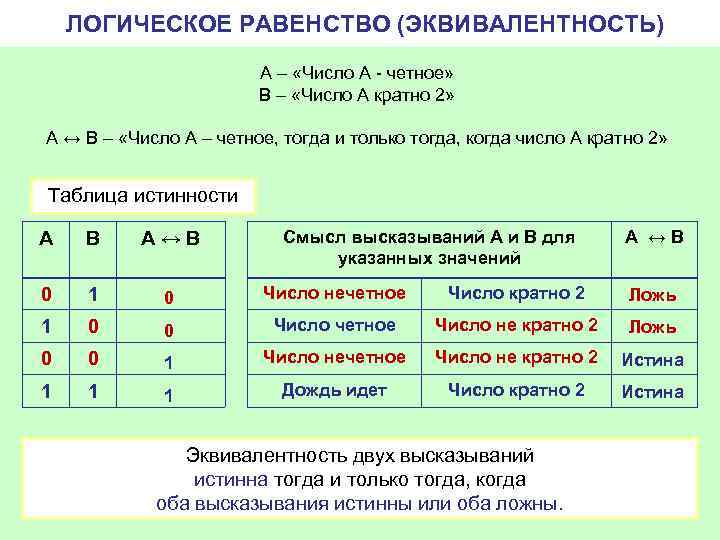
ЛОГИЧЕСКОЕ РАВЕНСТВО (ЭКВИВАЛЕНТНОСТЬ) А – «Число А - четное» В – «Число А кратно 2» А ↔ B – «Число А – четное, тогда и только тогда, когда число А кратно 2» Таблица истинности Смысл высказываний А и В для указанных значений А ↔B А В А↔B 0 1 0 Число нечетное Число кратно 2 Ложь 1 0 0 Число четное Число не кратно 2 Ложь 0 0 1 Число нечетное Число не кратно 2 Истина 1 1 1 Дождь идет Число кратно 2 Истина Эквивалентность двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или оба ложны.

Порядок операций: 1. Действия в скобках 2. Инверсия 3. Конъюнкция 4. Дизъюнкция 5. Импликация 6. Эквивалентность Пример: 1 2 4 3 не А и В или А и В

Проверка материала o o o Понятие - это форма мышление, фиксирующая основные, существенные признаки объекта, которые отличают его от других объектов. Высказывание - это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними. Высказывание может быть либо истинно, либо ложно. Суждения – это некоторые высказывания, которые могут быть истинными или ложными

Вопрос 1: Посчитайте, сколько понятий и суждений в следующем отрывке: Ветер по морю гуляет И кораблик подгоняет; Он бежит себе в волнах На поднятых парусах Мимо острова крутого, Мимо берега большого; Пушки с пристани палят, Кораблю пристать велят.

Ответ: Понятий – 9, суждений – 7. Понятия – Ветер, море, кораблик, волна, паруса, остров, берег, пушка, пристань. Суждения - Ветер по морю гуляет, И кораблик подгоняет; Он бежит себе в волнах Мимо острова крутого, Мимо берега большого; Пушки с пристани палят, Кораблю пристать велят.

Вопрос 2: Пришла весна, потекла вода. Дети взяли дощечки, сделали лодочку, пустили лодочку по воде. Лодочка плыла, а дети бежали за нею, кричали, и ничего впереди себя не видели, и в лужу упали” (Л. Н. Толстой).

Ответ: o o Понятия: “весна”, “вода”, “ребенок”, “дощечка”, “лодочка”, “лужа”. Суждения: “Весна пришла”, “Вода потекла”, “Дети взяли дощечки”, “Дети сделали лодочку”, “Дети пустили лодочку по воде”, “Лодочка плыла”, “Дети бежали за лодочкой”, “Дети кричали”, “Дети ничего впереди себя не видели”, “Дети упали в лужу”.

Вопрос 3: “Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников”.

Ответ: o o Понятия: “многогранник”, “тело”, “поверхность”, “число”, “многоугольник”. Суждения: “Многогранник – это тело”, “Поверхность состоит из конечного числа плоских многоугольников”