ffe12dd01515698037cec1d87d9fce11.ppt
- Количество слайдов: 35

Logic Gates 1

Review of Boolean algebra Just like Boolean logic Variables can only be 1 or 0 n Instead of true / false 2

Review of Boolean algebra Not is a horizontal bar above the number _ n n 0=1 _ 1=0 Or is a plus n n 0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 1 And is multiplication n n 0*0 = 0 0*1 = 0 1*0 = 0 1*1 = 1 3

Review of Boolean algebra ___ Example: translate (x+y+z)(xyz) to a Boolean logic expression n (x y z) ( x y z) We can define a Boolean function: n F(x, y) = (x y) ( x y) And then write a “truth table” for it: x y F(x, y) 1 1 0 0 0 1 0 0 4

Quick survey n a) b) c) d) I understand the basics of Boolean algebra Absolutely! More or less Not really Boolean what? 5

Today’s demotivators 6

Basic logic gates Not And Or Nand Nor Xor 7
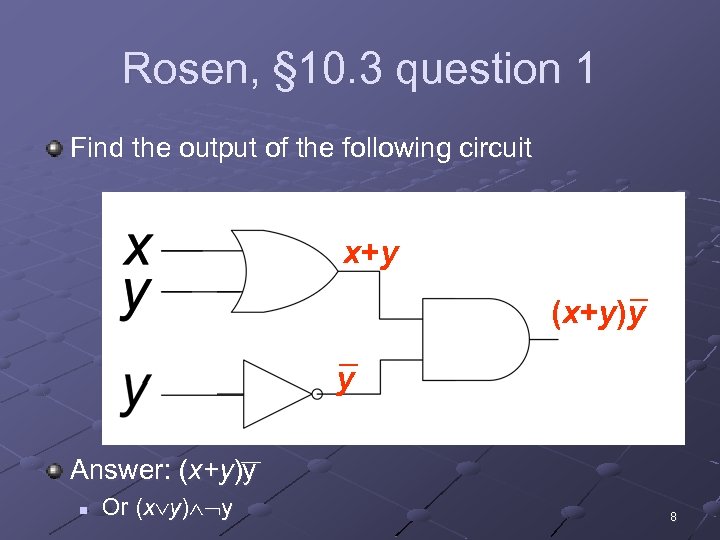
Rosen, § 10. 3 question 1 Find the output of the following circuit x+y (x+y)y y __ Answer: (x+y)y n Or (x y) y 8
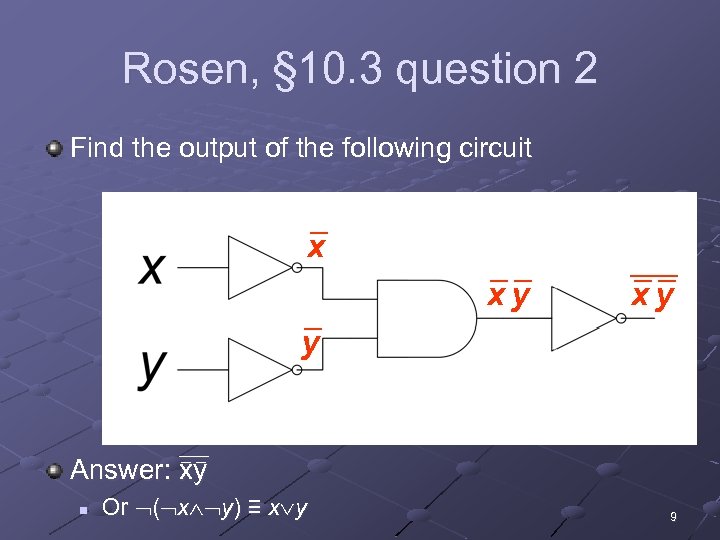
Rosen, § 10. 3 question 2 Find the output of the following circuit x xy xy y ___ __ Answer: xy n Or ( x y) ≡ x y 9

Quick survey n a) b) c) d) I understand how to figure out what a logic gate does Absolutely! More or less Not really Not at all 10
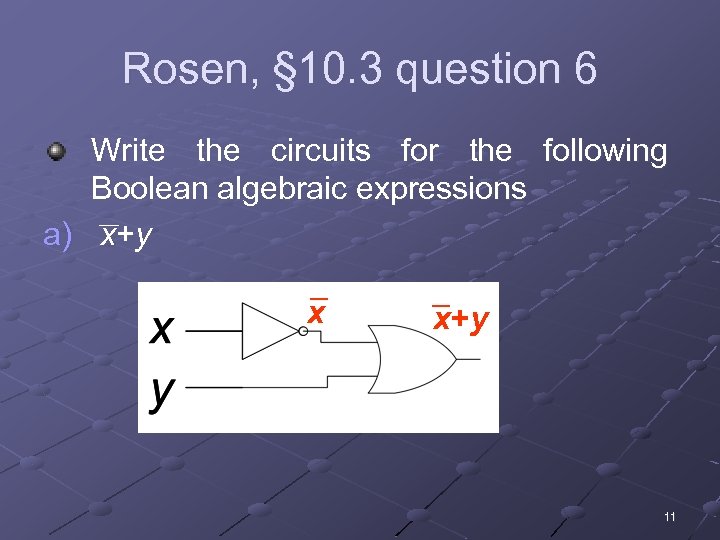
Rosen, § 10. 3 question 6 Write the circuits for the following Boolean algebraic expressions __ a) x+y x x+y 11
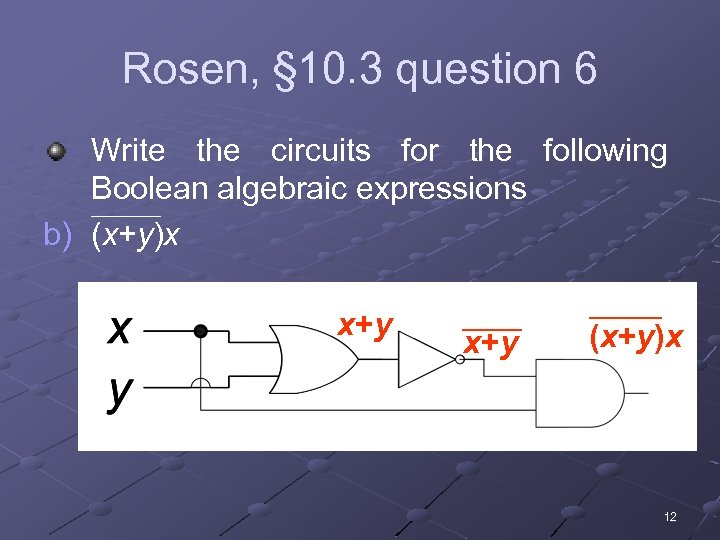
Rosen, § 10. 3 question 6 Write the circuits for the following Boolean algebraic expressions _______ b) (x+y)x x+y (x+y)x 12
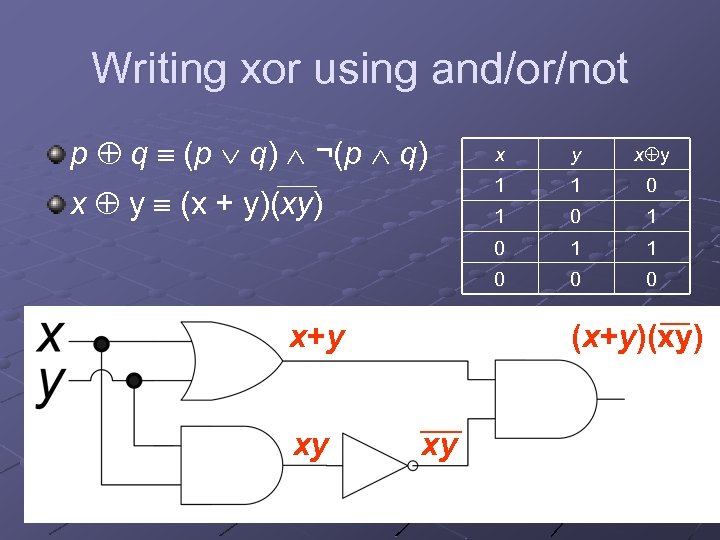
Writing xor using and/or/not p q (p q) ¬(p q) 0 0 1 1 1 0 xy 1 0 x+y x y 1 x y (x + y)(xy) y 1 ____ x 0 0 (x+y)(xy) xy 13

Quick survey n a) b) c) d) I understand how to write a logic circuit for simple Boolean formula Absolutely! More or less Not really Not at all 14

Converting decimal numbers to binary 53 = 32 + 16 + 4 + 1 = 25 + 2 4 + 2 2 + 2 0 = 1*25 + 1*24 + 0*23 + 1*22 + 0*21 + 1*20 = 110101 in binary = 00110101 as a full byte in binary 211= 128 + 64 + 16 + 2 + 1 = 27 + 2 6 + 2 4 + 2 1 + 2 0 = 1*27 + 1*26 + 0*25 + 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 11010011 in binary 15

Converting binary numbers to decimal What is 10011010 in decimal? 10011010 = 1*27 + 0*26 + 0*25 + 1*24 + 1*23 + 0*22 + 1*21 + 0*20 = 2 7 + 24 + 23 + 21 = 128 + 16 + 8 + 2 = 154 What is 00101001 in decimal? 00101001 = 0*27 + 0*26 + 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 2 5 + 23 + 20 = 32 + 8 + 1 = 41 16

A bit of binary humor n Available for $15 at http: //www. thinkgeek. com/ tshirts/frustrations/5 aa 9/ 17

Quick survey n a) b) c) d) I understand the basics of converting numbers between decimal and binary Absolutely! More or less Not really Not at all 18

How to add binary numbers Consider adding two 1 -bit binary numbers x and y n n 0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 10 x 0 0 1 1 y 0 1 Carry Sum 0 0 0 1 1 0 Carry is x AND y Sum is x XOR y The circuit to compute this is called a half-adder 19
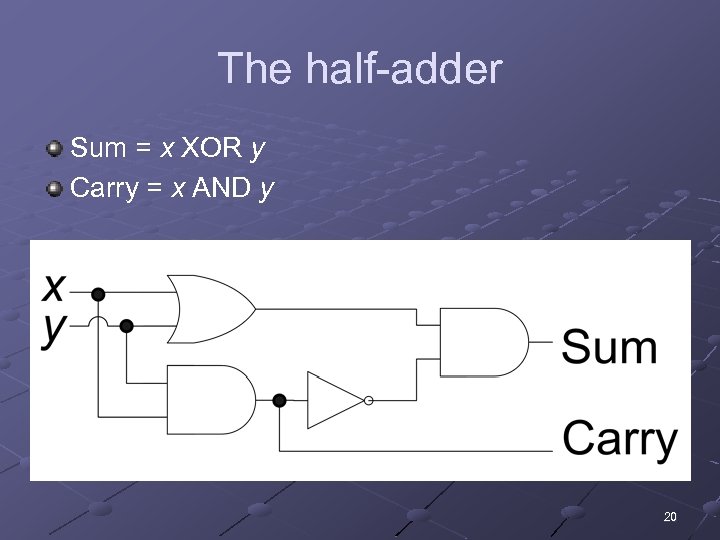
The half-adder Sum = x XOR y Carry = x AND y 20

Using half adders We can then use a half-adder to compute the sum of two Boolean numbers 1 1 +1 ? 0 1 1 0 0 1 0 21

Quick survey n a) b) c) d) I understand half adders Absolutely! More or less Not really Not at all 22

How to fix this We need to create an adder that can take a carry bit as an additional input n n Inputs: x, y, carry in Outputs: sum, carry out This is called a full adder n n Will add x and y with a half-adder Will add the sum of that to the carry in What about the carry out? n n n It’s 1 if either (or both): x+y = 10 x+y = 01 and carry in = 1 x 1 1 1 y 1 1 0 0 0 1 1 0 0 c carry sum 1 1 1 0 0 0 1 1 0 0 0 23
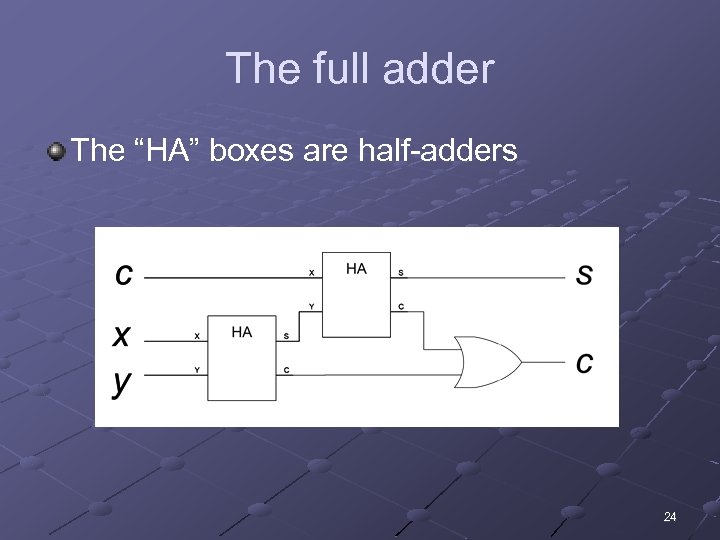
The full adder The “HA” boxes are half-adders 24
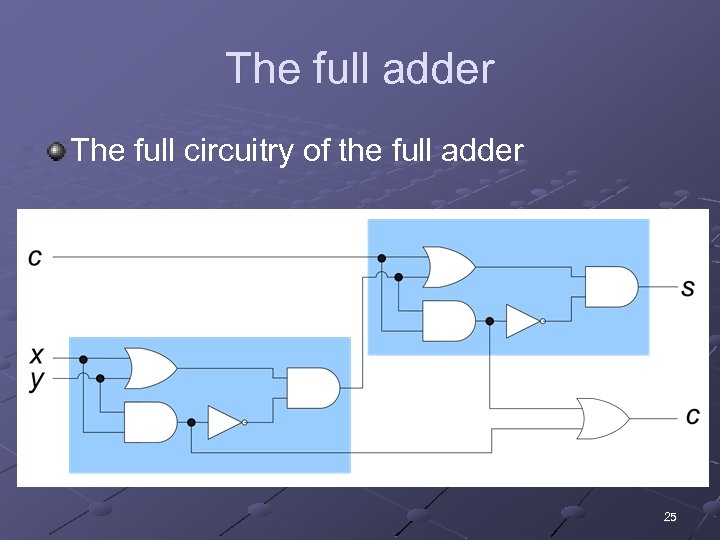
The full adder The full circuitry of the full adder 25
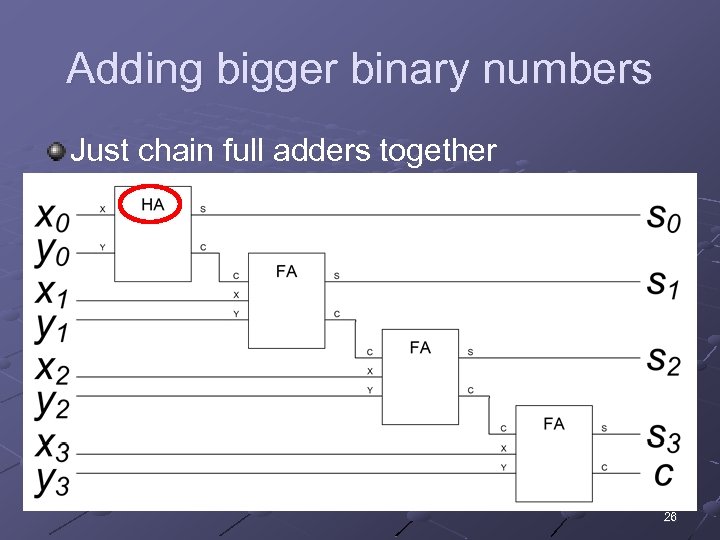
Adding bigger binary numbers Just chain full adders together 26

Adding bigger binary numbers A half adder has 4 logic gates A full adder has two half adders plus a OR gate n Total of 9 logic gates To add n bit binary numbers, you need 1 HA and n-1 FAs To add 32 bit binary numbers, you need 1 HA and 31 FAs n Total of 4+9*31 = 283 logic gates To add 64 bit binary numbers, you need 1 HA and 63 FAs n Total of 4+9*63 = 571 logic gates 27

Quick survey n a) b) c) d) I understand (more or less) about adding binary numbers using logic gates Absolutely! More or less Not really Not at all 28

More about logic gates To implement a logic gate in hardware, you use a transistor Transistors are all enclosed in an “IC”, or integrated circuit The current Intel Pentium IV processors have 55 million transistors! 29
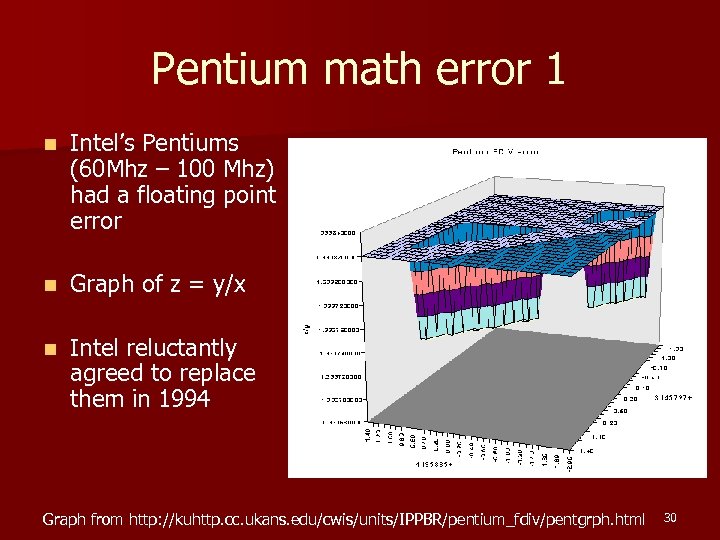
Pentium math error 1 n Intel’s Pentiums (60 Mhz – 100 Mhz) had a floating point error n Graph of z = y/x n Intel reluctantly agreed to replace them in 1994 Graph from http: //kuhttp. cc. ukans. edu/cwis/units/IPPBR/pentium_fdiv/pentgrph. html 30

Pentium math error 2 n Top 10 reasons to buy a Pentium: 10 8. 9999163362 7. 9999414610 6. 9999831538 5. 9999835137 4. 9999999021 3. 9998245917 2. 9991523619 1. 9999103517 0. 999998 Your old PC is too accurate Provides a good alibi when the IRS calls Attracted by Intel's new "You don't need to know what's inside" campaign It redefines computing--and mathematics! You've always wondered what it would be like to be a plaintiff Current paperweight not big enough Takes concept of "floating point" to a new level You always round off to the nearest hundred anyway Got a great deal from the Jet Propulsion Laboratory 31 It'll probably work!!
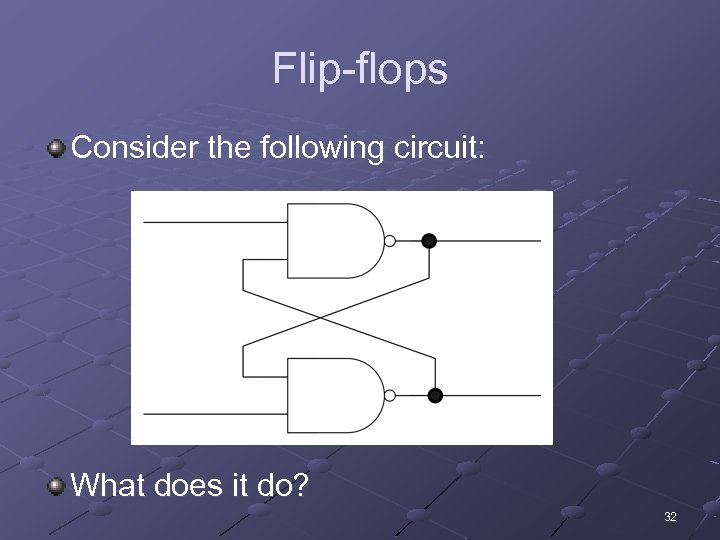
Flip-flops Consider the following circuit: What does it do? 32

Memory A flip-flop holds a single bit of memory n The bit “flip-flops” between the two NAND gates In reality, flip-flops are a bit more complicated n Have 5 (or so) logic gates (transistors) per flipflop Consider a 1 Gb memory chip n n 1 Gb = 8, 589, 934, 592 bits of memory That’s about 43 million transistors! In reality, those transistors are split into 9 ICs of about 5 million transistors each 33

Quick survey n a) b) c) d) I felt I understood the material in this slide set… Very well With some review, I’ll be good Not really Not at all 34

Quick survey n a) b) c) d) The pace of the lecture for this slide set was… Fast About right A little slow Too slow 35
ffe12dd01515698037cec1d87d9fce11.ppt