Logic and Computer Design Fundamentals Chapter 2

Logic and Computer Design Fundamentals Chapter 2 – Combinational Logic Circuits Part 1 – Gate Circuits and Boolean Equations Charles Kime & Thomas Kaminski © 2008 Pearson Education, Inc. (Hyperlinks are active in View Show mode)

Overview § Part 1 – Gate Circuits and Boolean Equations • Binary Logic and Gates • Boolean Algebra • Standard Forms § Part 2 – Circuit Optimization • • Two-Level Optimization Map Manipulation Practical Optimization (Espresso) Multi-Level Circuit Optimization § Part 3 – Additional Gates and Circuits • Other Gate Types • Exclusive-OR Operator and Gates • High-Impedance Outputs Chapter 2 - Part 1 2

Binary Logic and Gates § Binary variables take on one of two values. § Logical operators operate on binary values and binary variables. § Basic logical operators are the logic functions AND, OR and NOT. § Logic gates implement logic functions. § Boolean Algebra: a useful mathematical system for specifying and transforming logic functions. § We study Boolean algebra as a foundation for designing and analyzing digital systems! Chapter 2 - Part 1 3

Binary Variables § Recall that the two binary values have different names: • • True/False On/Off Yes/No 1/0 § We use 1 and 0 to denote the two values. § Variable identifier examples: • A, B, y, z, or X 1 for now • RESET, START_IT, or ADD 1 later Chapter 2 - Part 1 4

Logical Operations § The three basic logical operations are: • AND • OR • NOT § AND is denoted by a dot (·). § OR is denoted by a plus (+). § NOT is denoted by an overbar ( ¯ ), a single quote mark (') after, or (~) before the variable. Chapter 2 - Part 1 5

Notation Examples § Examples: • Y = A B is read “Y is equal to A AND B. ” • z = x + y is read “z is equal to x OR y. ” • X = A is read “X is equal to NOT A. ” § Note: The statement: 1 + 1 = 2 (read “one plus one equals two”) is not the same as 1 + 1 = 1 (read “ 1 or 1 equals 1”). Chapter 2 - Part 1 6

Operator Definitions § Operations are defined on the values "0" and "1" for each operator: AND 0· 0=0 0· 1=0 1· 0=0 1· 1=1 OR NOT 0+0=0 0+1=1 1+0=1 1+1=1 0=1 1=0 Chapter 2 - Part 1 7

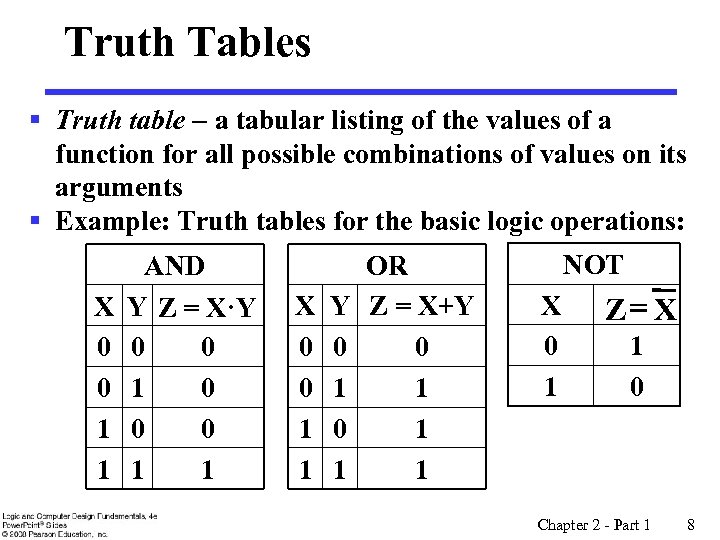Truth Tables § Truth table - a tabular listing of the values of a function for all possible combinations of values on its arguments § Example: Truth tables for the basic logic operations: X 0 0 1 1 AND Y Z = X·Y 0 0 1 0 0 0 1 1 X 0 0 1 1 Y 0 1 OR Z = X+Y 0 1 1 1 NOT X 0 1 Z=X 1 0 Chapter 2 - Part 1 8

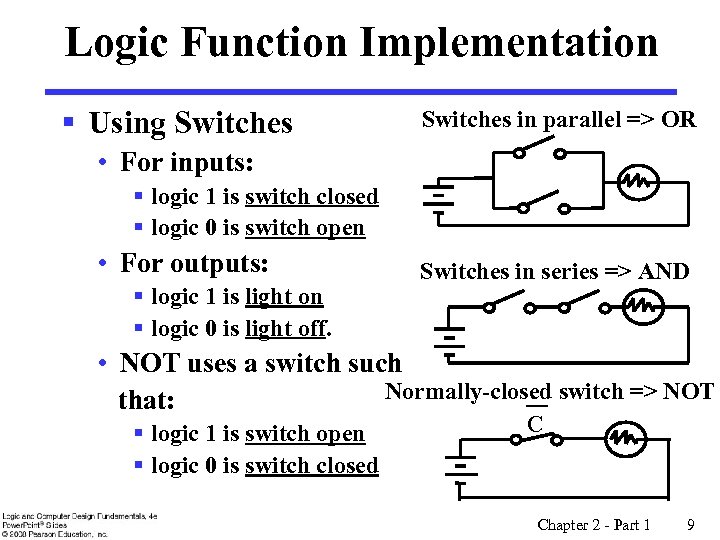Logic Function Implementation § Using Switches in parallel => OR • For inputs: § logic 1 is switch closed § logic 0 is switch open • For outputs: § logic 1 is light on § logic 0 is light off. Switches in series => AND • NOT uses a switch such Normally-closed switch => NOT that: § logic 1 is switch open § logic 0 is switch closed C Chapter 2 - Part 1 9

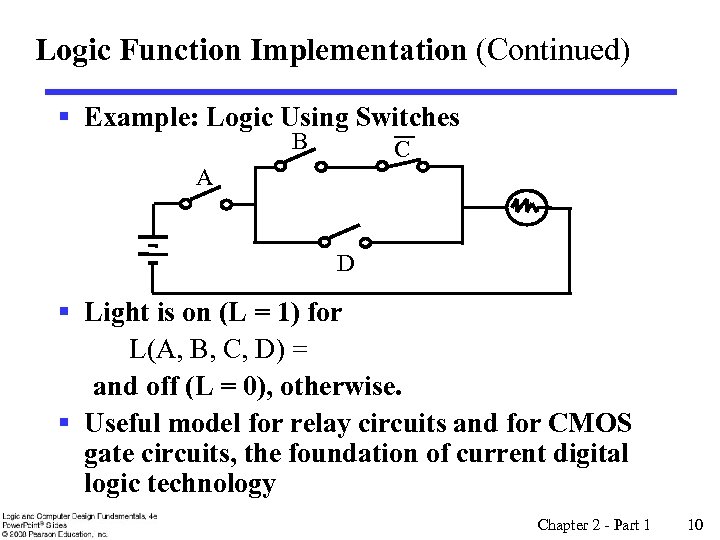Logic Function Implementation (Continued) § Example: Logic Using Switches B C A D § Light is on (L = 1) for L(A, B, C, D) = and off (L = 0), otherwise. § Useful model for relay circuits and for CMOS gate circuits, the foundation of current digital logic technology Chapter 2 - Part 1 10

Logic Gates § In the earliest computers, switches were opened and closed by magnetic fields produced by energizing coils in relays. The switches in turn opened and closed the current paths. § Later, vacuum tubes that open and close current paths electronically replaced relays. § Today, transistors are used as electronic switches that open and close current paths. § Optional: Chapter 6 – Part 1: The Design Space Chapter 2 - Part 1 11

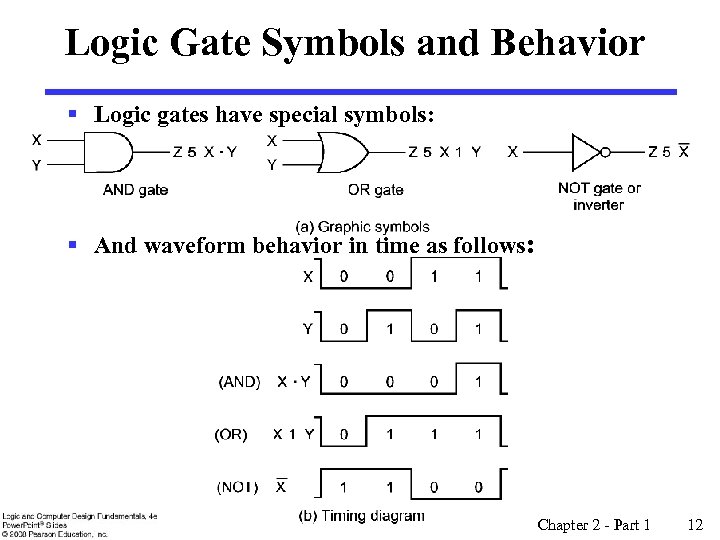Logic Gate Symbols and Behavior § Logic gates have special symbols: § And waveform behavior in time as follows: Chapter 2 - Part 1 12

Gate Delay § In actual physical gates, if one or more input changes causes the output to change, the output change does not occur instantaneously. § The delay between an input change(s) and the resulting output change is the gate delay denoted by t. G: 1 Input 0 1 Output 0 0 t. G 0. 5 1 t. G = 0. 3 ns 1. 5 Time (ns) Chapter 2 - Part 1 13

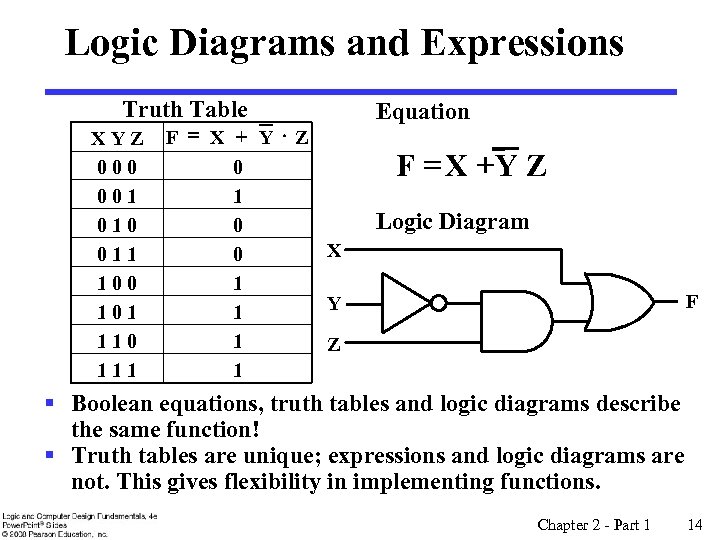Logic Diagrams and Expressions Truth Table XYZ 000 001 010 011 100 101 110 111 F = X + Y Z 0 1 0 X 0 1 Y 1 1 Z 1 Equation F = X +Y Z Logic Diagram F § Boolean equations, truth tables and logic diagrams describe the same function! § Truth tables are unique; expressions and logic diagrams are not. This gives flexibility in implementing functions. Chapter 2 - Part 1 14

Boolean Algebra § 1. 3. 5. 7. 9. An algebraic structure defined on a set of at least two elements, B, together with three binary operators (denoted +, · and ) that satisfies the following basic identities: X+0= X X+1 =1 X+X =X X+X =1 2. 4. 6. 8. X. 1 =X X. 0 =0 X. X = X X. X = 0 X=X 10. X + Y = Y + X 12. (X + Y) + Z = X + (Y + Z) 14. X(Y + Z) = XY + XZ 16. X + Y = X. Y 11. XY = YX Commutative Associative 13. (XY) Z = X(YZ) 15. X + YZ = (X + Y) (X + Z) Distributive De. Morgan’s 17. X. Y = X + Y Chapter 2 - Part 1 15

Some Properties of Identities & the Algebra § If the meaning is unambiguous, we leave out the symbol “·” § The identities above are organized into pairs. These pairs have names as follows: 1 -4 Existence of 0 and 1 5 -6 Idempotence 7 -8 Existence of complement 9 Involution 10 -11 Commutative Laws 12 -13 Associative Laws 14 -15 Distributive Laws 16 -17 De. Morgan’s Laws § The dual of an algebraic expression is obtained by interchanging + and · and interchanging 0’s and 1’s. § The identities appear in dual pairs. When there is only one identity on a line the identity is self-dual, i. e. , the dual expression = the original expression. Chapter 2 - Part 1 16

Some Properties of Identities & the Algebra (Continued) § Unless it happens to be self-dual, the dual of an expression does not equal the expression itself. § Example: F = (A + C) · B + 0 dual F = (A · C + B) · 1 = A · C + B § Example: G = X · Y + (W + Z) dual G = § Example: H = A · B + A · C + B · C dual H = § Are any of these functions self-dual? Chapter 2 - Part 1 17

Some Properties of Identities & the Algebra (Continued) § There can be more that 2 elements in B, i. e. , elements other than 1 and 0. What are some common useful Boolean algebras with more than 2 elements? 1. Algebra of Sets 2. Algebra of n-bit binary vectors § If B contains only 1 and 0, then B is called the switching algebra which is the algebra we use most often. Chapter 2 - Part 1 18

Boolean Operator Precedence § The order of evaluation in a Boolean expression is: 1. Parentheses 2. NOT 3. AND 4. OR § Consequence: Parentheses appear around OR expressions § Example: F = A(B + C)(C + D) Chapter 2 - Part 1 19

Example 1: Boolean Algebraic Proof § A + A·B = A (Absorption Theorem) Proof Steps Justification (identity or theorem) A + A·B = A· 1+A·B X = X · 1 = A · ( 1 + B) X · Y + X · Z = X ·(Y + Z)(Distributive Law) = A · 1 1 + X = 1 =A X· 1=X § Our primary reason for doing proofs is to learn: • Careful and efficient use of the identities and theorems of Boolean algebra, and • How to choose the appropriate identity or theorem to apply to make forward progress, irrespective of the application. Chapter 2 - Part 1 20

Example 2: Boolean Algebraic Proofs § AB + AC + BC = AB + AC (Consensus Theorem) Proof Steps Justification (identity or theorem) AB + AC + BC = AB + AC + 1 · BC ? = AB +AC + (A + A) · BC ? = Chapter 2 - Part 1 21

Example 3: Boolean Algebraic Proofs § ( X + Y ) Z + X Y = Y( X + Z ) Proof Steps Justification (identity or theorem) ( X + Y )Z + X Y = Chapter 2 - Part 1 22

Useful Theorems § § x y + x y = y (x + y )= y x + x y = x + y x (x + y )= x y + x z + y z = x y + x z Minimization Simplification Consensus (x + y ) (x + z ) (y + z ) = (x + y ) (x + z ) § x + y = x y x y = x + y De. Morgan' s Laws Chapter 2 - Part 1 23

Proof of Simplification x y + x y = y (x + y ) = y Chapter 2 - Part 1 24

Proof of De. Morgan’s Laws x + y = x + y Chapter 2 - Part 1 25

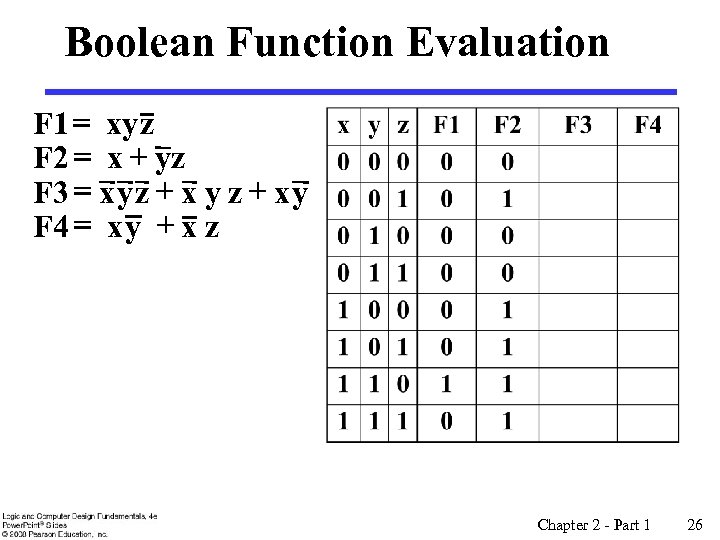Boolean Function Evaluation F 1 = xy z F 2 = x + yz F 3 = x y z + x y F 4 = x y + x z Chapter 2 - Part 1 26

Expression Simplification § An application of Boolean algebra § Simplify to contain the smallest number of literals (complemented and uncomplemented variables): A B + ACD + A BD + AC D + A BCD = AB + ABCD + A C D + A B D = AB + AB(CD) + A C (D + D) + A B D = AB + A C + A B D = B(A + AD) +AC = B (A + D) + A C 5 literals Chapter 2 - Part 1 27

Complementing Functions § Use De. Morgan's Theorem to complement a function: 1. Interchange AND and OR operators 2. Complement each constant value and literal § Example: Complement F = xy z + x y z F = (x + y + z) § Example: Complement G = (a + bc)d + e G= Chapter 2 - Part 1 28

Overview – Canonical Forms § What are Canonical Forms? § Minterms and Maxterms § Index Representation of Minterms and Maxterms § Sum-of-Minterm (SOM) Representations § Product-of-Maxterm (POM) Representations § Representation of Complements of Functions § Conversions between Representations Chapter 2 - Part 1 29

Canonical Forms § It is useful to specify Boolean functions in a form that: • Allows comparison for equality. • Has a correspondence to the truth tables § Canonical Forms in common usage: • Sum of Minterms (SOM) • Product of Maxterms (POM) Chapter 2 - Part 1 30

Minterms § Minterms are AND terms with every variable present in either true or complemented form. § Given that each binary variable may appear normal (e. g. , x) or complemented (e. g. , x), there are 2 n minterms for n variables. § Example: Two variables (X and Y)produce 2 x 2 = 4 combinations: XY (both normal) X Y (X normal, Y complemented) XY (X complemented, Y normal) X Y (both complemented) § Thus there are four minterms of two variables. Chapter 2 - Part 1 31

Maxterms § Maxterms are OR terms with every variable in true or complemented form. § Given that each binary variable may appear normal (e. g. , x) or complemented (e. g. , x), there are 2 n maxterms for n variables. § Example: Two variables (X and Y) produce 2 x 2 = 4 combinations: X + Y (both normal) X + Y (x normal, y complemented) X + Y (x complemented, y normal) X + Y (both complemented) Chapter 2 - Part 1 32

Maxterms and Minterms § Examples: Two variable minterms and maxterms. Index Minterm Maxterm 0 xy x+y 1 xy x+y 2 xy x+y 3 xy x+y § The index above is important for describing which variables in the terms are true and which are complemented. Chapter 2 - Part 1 33

Standard Order § Minterms and maxterms are designated with a subscript § The subscript is a number, corresponding to a binary pattern § The bits in the pattern represent the complemented or normal state of each variable listed in a standard order. § All variables will be present in a minterm or maxterm and will be listed in the same order (usually alphabetically) § Example: For variables a, b, c: • Maxterms: (a + b + c), (a + b + c) • Terms: (b + a + c), a c b, and (c + b + a) are NOT in standard order. • Minterms: a b c, a b c • Terms: (a + c), b c, and (a + b) do not contain all variables Chapter 2 - Part 1 34

Purpose of the Index § The index for the minterm or maxterm, expressed as a binary number, is used to determine whether the variable is shown in the true form or complemented form. § For Minterms: • “ 1” means the variable is “Not Complemented” and • “ 0” means the variable is “Complemented”. § For Maxterms: • “ 0” means the variable is “Not Complemented” and • “ 1” means the variable is “Complemented”. Chapter 2 - Part 1 35

Index Example in Three Variables § § Example: (for three variables) Assume the variables are called X, Y, and Z. The standard order is X, then Y, then Z. The Index 0 (base 10) = 000 (base 2) for three variables). All three variables are complemented for minterm 0 ( X , Y, Z) and no variables are complemented for Maxterm 0 (X, Y, Z). • • Minterm 0, called m 0 is X Y Z. Maxterm 0, called M 0 is (X + Y + Z). Minterm 6 ? Maxterm 6 ? Chapter 2 - Part 1 36

Index Examples – Four Variables Index i 0 1 3 5 7 10 13 15 Binary Minterm Pattern mi abcd 0000 0001 abcd ? 0011 0101 abcd ? 0111 1010 abcd 1101 1111 Maxterm Mi ? a+b+c+d ? a+b+c+d Chapter 2 - Part 1 37

Minterm and Maxterm Relationship § Review: De. Morgan's Theorem x · y = x + y and x + y = x y § Two-variable example: M 2 = x + y and m 2 = x·y Thus M 2 is the complement of m 2 and vice-versa. § Since De. Morgan's Theorem holds for n variables, the above holds for terms of n variables § giving: M i = m i and m i = M i Thus Mi is the complement of mi. Chapter 2 - Part 1 38

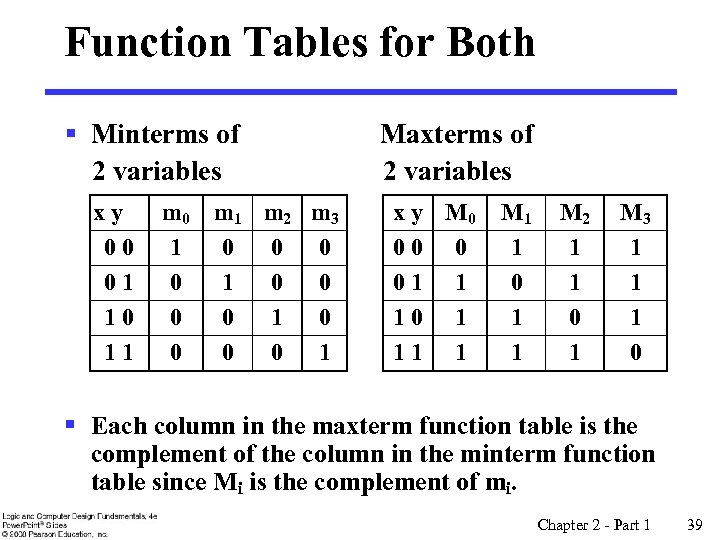Function Tables for Both § Minterms of 2 variables xy 00 01 10 11 m 0 1 0 0 0 m 1 m 2 m 3 0 0 0 1 Maxterms of 2 variables x y M 0 00 0 01 1 10 1 11 1 M 1 1 0 1 1 M 2 1 1 0 1 M 3 1 1 1 0 § Each column in the maxterm function table is the complement of the column in the minterm function table since Mi is the complement of mi. Chapter 2 - Part 1 39

Observations § In the function tables: • Each minterm has one and only one 1 present in the 2 n terms (a minimum of 1 s). All other entries are 0. • Each maxterm has one and only one 0 present in the 2 n terms All other entries are 1 (a maximum of 1 s). § We can implement any function by "ORing" the minterms corresponding to "1" entries in the function table. These are called the minterms of the function. § We can implement any function by "ANDing" the maxterms corresponding to "0" entries in the function table. These are called the maxterms of the function. § This gives us two canonical forms: • Sum of Minterms (SOM) • Product of Maxterms (POM) for stating any Boolean function. Chapter 2 - Part 1 40

Minterm Function Example § Example: Find F 1 = m 1 + m 4 + m 7 § F 1 = x y z + x y z index m 1 + m 4 + m 7 = F 1 000 0 0 + 0 =0 001 1 1 + 0 =1 010 2 0 + 0 =0 011 3 0 + 0 =0 100 4 0 + 1 + 0 =1 101 5 0 + 0 =0 110 6 0 + 0 =0 111 7 0 + 1 =1 Chapter 2 - Part 1 41

Minterm Function Example § F(A, B, C, D, E) = m 2 + m 9 + m 17 + m 23 § F(A, B, C, D, E) = Chapter 2 - Part 1 42

Maxterm Function Example § Example: Implement F 1 in maxterms: F 1 = M 0 · M 2 · M 3 · M 5 · M 6 F 1 = (x + y + z) ·(x + y + z)·(x + y + z ) ·(x + y + z )·(x + y + z) xyz 000 001 010 011 100 101 110 111 i 0 1 2 3 4 5 6 7 M 0 M 2 M 3 M 5 M 6 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 = F 1 =0 =0 =1 Chapter 2 - Part 1 43

Maxterm Function Example § F( A, B, C, D) = M 3 M 8 M 11 M 14 § F(A, B, C, D) = Chapter 2 - Part 1 44

Canonical Sum of Minterms § Any Boolean function can be expressed as a Sum of Minterms. • For the function table, the minterms used are the terms corresponding to the 1's • For expressions, expand all terms first to explicitly list all minterms. Do this by “ANDing” any term missing a variable v with a term (v + v ). § Example: Implement f = x + x y as a sum of minterms. First expand terms: f = x ( y + y ) + x y Then distribute terms: f = xy + x y Express as sum of minterms: f = m 3 + m 2 + m 0 Chapter 2 - Part 1 45

Another SOM Example § Example: F = A + B C § There are three variables, A, B, and C which we take to be the standard order. § Expanding the terms with missing variables: § Collect terms (removing all but one of duplicate terms): § Express as SOM: Chapter 2 - Part 1 46

Shorthand SOM Form § From the previous example, we started with: F=A+BC § We ended up with: F = m 1+m 4+m 5+m 6+m 7 § This can be denoted in the formal shorthand: § Note that we explicitly show the standard variables in order and drop the “m” designators. Chapter 2 - Part 1 47

Canonical Product of Maxterms § Any Boolean Function can be expressed as a Product of Maxterms (POM). • For the function table, the maxterms used are the terms corresponding to the 0's. • For an expression, expand all terms first to explicitly list all maxterms. Do this by first applying the second distributive law , “ORing” terms missing variable v with a term equal to and then applying the distributive law again. v v § Example: Convert to product of maxterms: f ( x, y , z ) = x + x y Apply the distributive law: x + x y = (x + x )(x + y ) = 1 (x + y ) = x + y Add missing variable z: x + y + z z = ( x + y + z ) (x + y + z ) Express as POM: f = M 2 · M 3 Chapter 2 - Part 1 48

Another POM Example § Convert to Product of Maxterms: f(A, B, C) = A C + B C + A B § Use x + y z = (x+y)·(x+z) with x = (A C + B C), y = A , and z = B to get: f = (A C + B C + A )(A C + B ) § Then use x + x y = x + y to get: f = ( C + BC + A )(A C + B ) and a second time to get: f = ( C + B + A )(A + C + B ) § Rearrange to standard order, to give f = M 5 · M 2 f = ( A + B + C)(A + B + C) Chapter 2 - Part 1 49

Function Complements § The complement of a function expressed as a sum of minterms is constructed by selecting the minterms missing in the sum-of-minterms canonical forms. § Alternatively, the complement of a function expressed by a Sum of Minterms form is simply the Product of Maxterms with the same indices. § Example: Given F ( x , y , z ) = Sm ( 1, 3 , 5 , 7 ) F( x, y , z ) = Sm( 0, 2, 4, 6) F( x, y , z ) = PM(1, 3, 5, 7 ) Chapter 2 - Part 1 50

Conversion Between Forms § To convert between sum-of-minterms and productof-maxterms form (or vice-versa) we follow these steps: • Find the function complement by swapping terms in the list with terms not in the list. • Change from products to sums, or vice versa. § Example: Given F as before: § Form the Complement: F( x, y , z ) = Sm( 0, 2, 4, 6) § Then use the other form with the same indices – this forms the complement again, giving the other form of the original function: Chapter 2 - Part 1 51

Standard Forms § Standard Sum-of-Products (SOP) form: equations are written as an OR of AND terms § Standard Product-of-Sums (POS) form: equations are written as an AND of OR terms § Examples: • SOP: A B C + B (A • POS: + B) · (A+ B + C )· C § These “mixed” forms are neither SOP nor POS • (A B + C) (A + C) • A B C + A C (A + B) Chapter 2 - Part 1 52

Standard Sum-of-Products (SOP) § A sum of minterms form for n variables can be written down directly from a truth table. • Implementation of this form is a two-level network of gates such that: • The first level consists of n-input AND gates, and • The second level is a single OR gate (with fewer than 2 n inputs). § This form often can be simplified so that the corresponding circuit is simpler. Chapter 2 - Part 1 53

Standard Sum-of-Products (SOP) § A Simplification Example: § § Writing the minterm expression: F = A B C + ABC § Simplifying: F= § Simplified F contains 3 literals compared to 15 in minterm F Chapter 2 - Part 1 54

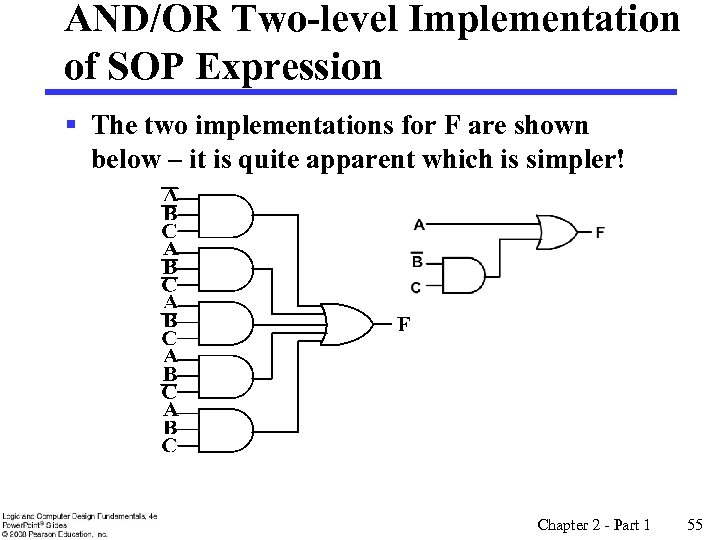AND/OR Two-level Implementation of SOP Expression § The two implementations for F are shown below – it is quite apparent which is simpler! Chapter 2 - Part 1 55

SOP and POS Observations § The previous examples show that: • Canonical Forms (Sum-of-minterms, Product-of. Maxterms), or other standard forms (SOP, POS) differ in complexity • Boolean algebra can be used to manipulate equations into simpler forms. • Simpler equations lead to simpler two-level implementations § Questions: • How can we attain a “simplest” expression? • Is there only one minimum cost circuit? • The next part will deal with these issues. Chapter 2 - Part 1 56

Circuit Optimization § Goal: To obtain the simplest implementation for a given function § Optimization is a more formal approach to simplification that is performed using a specific procedure or algorithm § Optimization requires a cost criterion to measure the simplicity of a circuit § Distinct cost criteria we will use: • Literal cost (L) • Gate input cost (G) • Gate input cost with NOTs (GN) Chapter 2 - Part 2 57

Literal Cost § Literal – a variable or it complement § Literal cost – the number of literal appearances in a Boolean expression corresponding to the logic circuit diagram § Examples: • • F = BD + A B C + A C D F = BD + A B C + A B D + AB C F = (A + B)(A + D)(B + C + D )( B + Which solution is best? C L=8 L= + D) L = Chapter 2 - Part 2 58

Gate Input Cost § Gate input costs - the number of inputs to the gates in the implementation corresponding exactly to the given equation or equations. (G - inverters not counted, GN - inverters counted) § For SOP and POS equations, it can be found from the equation(s) by finding the sum of: • all literal appearances • the number of terms excluding single literal terms, (G) and • optionally, the number of distinct complemented single literals (GN). § Example: • F = BD + A B C + A C D G = 12, GN = 15 • F = BD + A B C + A B D + AB C G = , GN = • F = (A + B)(A + D)(B + C + D )( B + C + D) G = , GN = • Which solution is best? Chapter 2 - Part 2 59

Cost Criteria (continued) § Example 1: § F=A+BC+ B C GN = G + 2 = 9 L=5 G=L+2= 7 B C A F § L (literal count) counts the AND inputs and the single literal OR input. § G (gate input count) adds the remaining OR gate inputs § GN(gate input count with NOTs) adds the inverter inputs Chapter 2 - Part 2 60

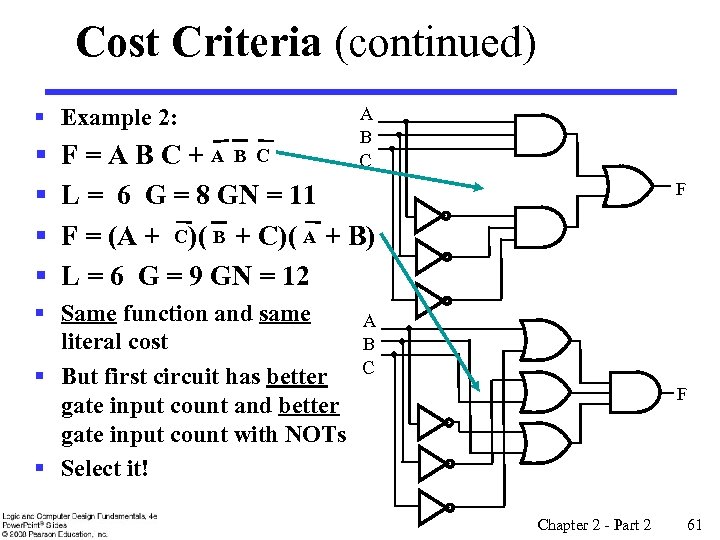Cost Criteria (continued) § Example 2: § § A B C F=ABC+AB C L = 6 G = 8 GN = 11 F = (A + C )( B + C)( A + B) L = 6 G = 9 GN = 12 § Same function and same literal cost § But first circuit has better gate input count and better gate input count with NOTs § Select it! F A B C F Chapter 2 - Part 2 61

Boolean Function Optimization § Minimizing the gate input (or literal) cost of a (a set of) Boolean equation(s) reduces circuit cost. § We choose gate input cost. § Boolean Algebra and graphical techniques are tools to minimize cost criteria values. § Some important questions: • When do we stop trying to reduce the cost? • Do we know when we have a minimum cost? § Treat optimum or near-optimum cost functions for two-level (SOP and POS) circuits first. § Introduce a graphical technique using Karnaugh maps (K-maps, for short) Chapter 2 - Part 2 62

Karnaugh Maps (K-map) § A K-map is a collection of squares • • Each square represents a minterm The collection of squares is a graphical representation of a Boolean function Adjacent squares differ in the value of one variable Alternative algebraic expressions for the same function are derived by recognizing patterns of squares § The K-map can be viewed as • A reorganized version of the truth table • A topologically-warped Venn diagram as used to visualize sets in algebra of sets Chapter 2 - Part 2 63

Some Uses of K-Maps § Provide a means for: • Finding optimum or near optimum § SOP and POS standard forms, and § two-level AND/OR and OR/AND circuit implementations for functions with small numbers of variables • Visualizing concepts related to manipulating Boolean expressions, and • Demonstrating concepts used by computeraided design programs to simplify large circuits Chapter 2 - Part 2 64

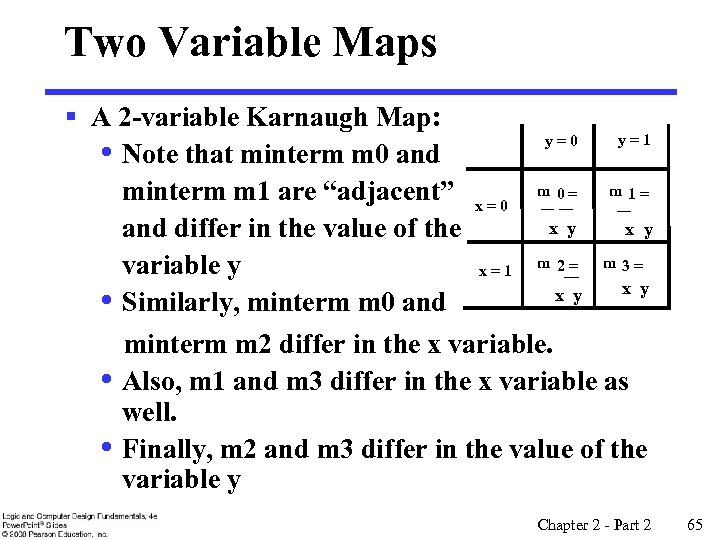Two Variable Maps § A 2 -variable Karnaugh Map: y=1 y=0 • Note that minterm m 0 and minterm m 1 are “adjacent” x = 0 m 0 = m 1 = x y and differ in the value of the m 2= m 3= variable y x=1 x y • Similarly, minterm m 0 and minterm m 2 differ in the x variable. • Also, m 1 and m 3 differ in the x variable as well. • Finally, m 2 and m 3 differ in the value of the variable y Chapter 2 - Part 2 65

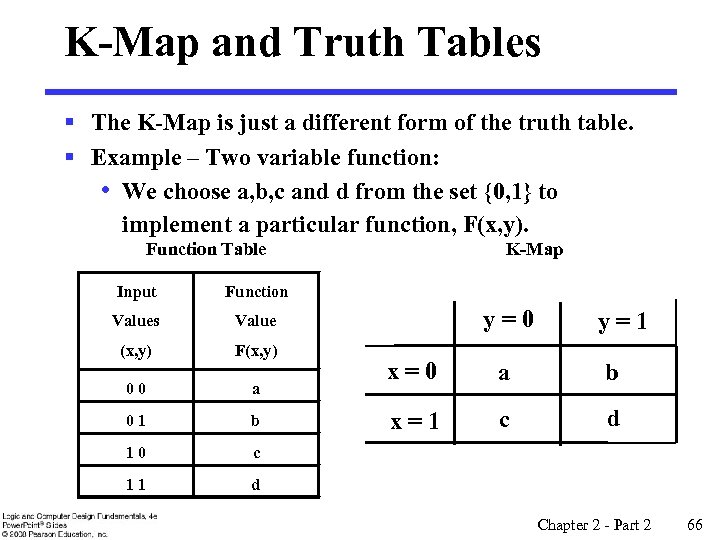K-Map and Truth Tables § The K-Map is just a different form of the truth table. § Example – Two variable function: • We choose a, b, c and d from the set {0, 1} to implement a particular function, F(x, y). K-Map Function Table Input Function Values Value (x, y) F(x, y) 00 a 01 b 10 c 11 d y=0 y=1 x=0 a b x=1 c d Chapter 2 - Part 2 66

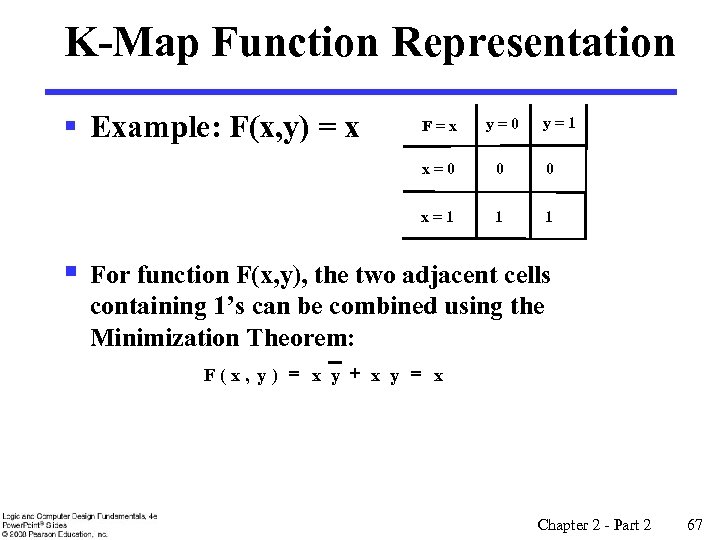K-Map Function Representation § Example: F(x, y) = x y=1 y=0 x=0 0 0 x=1 § F=x 1 1 For function F(x, y), the two adjacent cells containing 1’s can be combined using the Minimization Theorem: F(x, y ) = x y + x y = x Chapter 2 - Part 2 67

K-Map Function Representation § Example: G(x, y) = x + y y=1 G = x+y y=0 x=0 0 1 x=1 1 1 § For G(x, y), two pairs of adjacent cells containing 1’s can be combined using the Minimization Theorem: G(x, y ) = ( x y + x y )+ (xy + x y )= x + y Duplicate x y Chapter 2 - Part 2 68

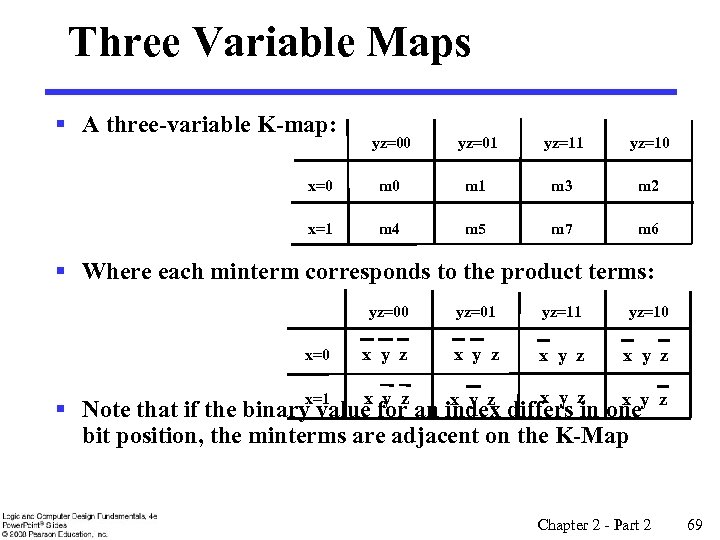Three Variable Maps § A three-variable K-map: yz=00 yz=01 yz=10 x=0 m 1 m 3 m 2 x=1 m 4 m 5 m 7 m 6 § Where each minterm corresponds to the product terms: yz=00 x=0 yz=01 yz=10 x y z x y z z x § Note that if the binary value for an index differs in oney bit position, the minterms are adjacent on the K-Map x=1 Chapter 2 - Part 2 69

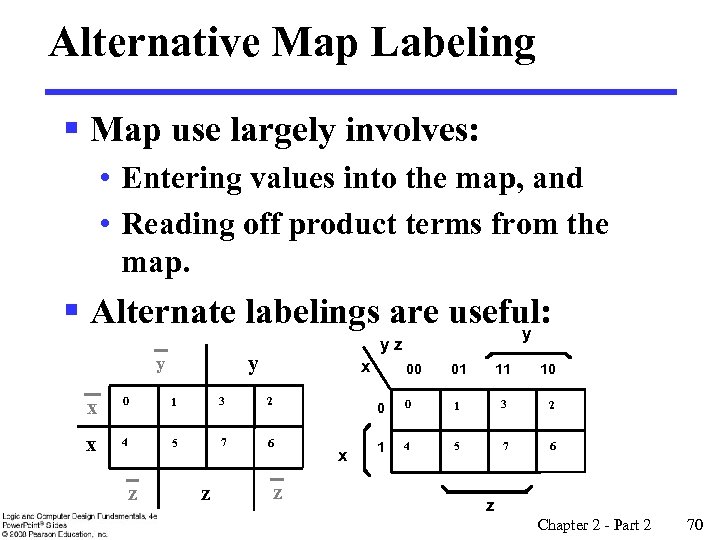Alternative Map Labeling § Map use largely involves: • Entering values into the map, and • Reading off product terms from the map. § Alternate labelings are useful: y yz y y x 0 1 3 2 x 4 5 7 6 z z z x 01 11 0 x 00 10 0 1 3 2 1 4 5 7 6 z Chapter 2 - Part 2 70

Example Functions § By convention, we represent the minterms of F by a "1" in the map and leave the minterms of F blank y § Example: 0 x 4 3 1 5 1 § Example: 2 1 7 1 1 6 z y § Learn the locations of the 8 indices based on the variable x order shown (x, most significant and z, least significant) on the map boundaries 0 4 1 1 3 1 2 5 7 1 6 1 z Chapter 2 - Part 2 71

Combining Squares § By combining squares, we reduce number of literals in a product term, reducing the literal cost, thereby reducing the other two cost criteria § On a 3 -variable K-Map: • One square represents a minterm with three variables • Two adjacent squares represent a product term with two variables • Four “adjacent” terms represent a product term with one variable • Eight “adjacent” terms is the function of all ones (no variables) = 1. Chapter 2 - Part 2 72

Example: Combining Squares y § Example: Let 0 x 1 3 1 2 1 4 5 7 1 6 1 z § Applying the Minimization Theorem three times: F(x, y, z) = x y z + x y z = yz + y z = y § Thus the four terms that form a 2 × 2 square correspond to the term "y". Chapter 2 - Part 2 73

Three-Variable Maps § Reduced literal product terms for SOP standard forms correspond to rectangles on K-maps containing cell counts that are powers of 2. § Rectangles of 2 cells represent 2 adjacent minterms; of 4 cells represent 4 minterms that form a “pairwise adjacent” ring. § Rectangles can contain non-adjacent cells as illustrated by the “pairwise adjacent” ring above. Chapter 2 - Part 2 74

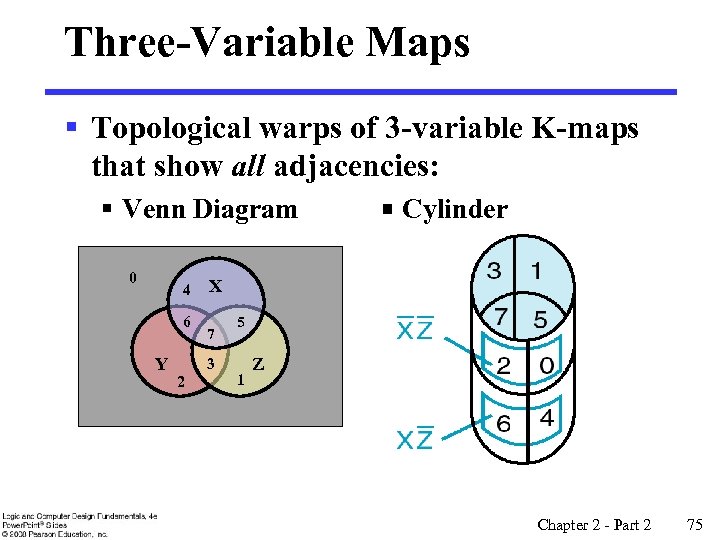Three-Variable Maps § Topological warps of 3 -variable K-maps that show all adjacencies: § Venn Diagram 0 4 6 Y Cylinder X 7 3 2 5 1 Z Chapter 2 - Part 2 75

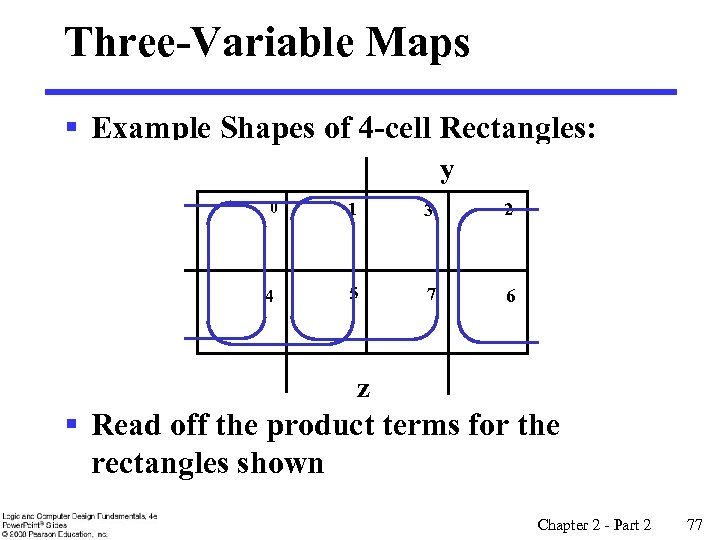
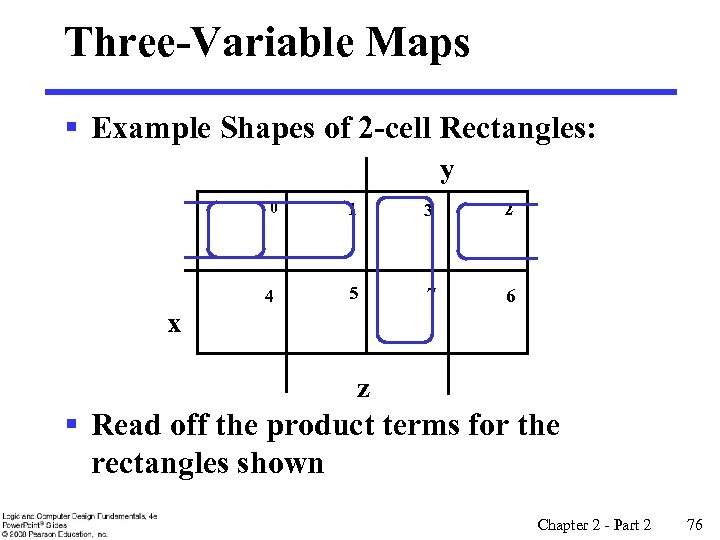Three-Variable Maps § Example Shapes of 2 -cell Rectangles: y 0 1 3 2 4 5 7 6 x z § Read off the product terms for the rectangles shown Chapter 2 - Part 2 76

Three-Variable Maps § Example Shapes of 4 -cell Rectangles: y 0 1 3 2 4 5 7 6 x z § Read off the product terms for the rectangles shown Chapter 2 - Part 2 77

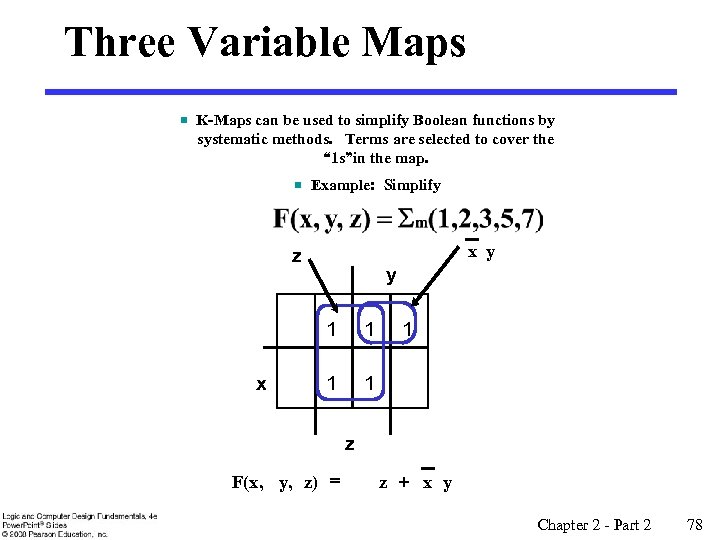Three Variable Maps § K-Maps can be used to simplify Boolean functions by systematic methods. Terms are selected to cover the “ 1 s”in the map. § Example: Simplify x y z y 1 x 1 1 z F(x, y, z) = z + x y Chapter 2 - Part 2 78

Three-Variable Map Simplification § Use a K-map to find an optimum SOP equation for Chapter 2 - Part 2 79

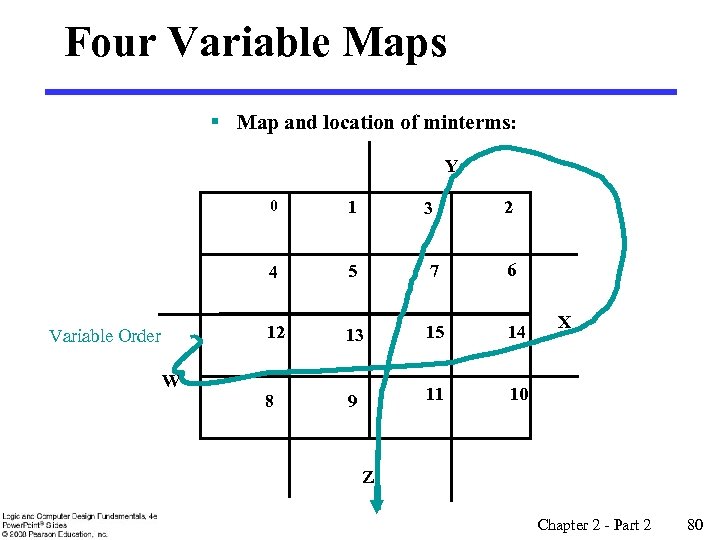Four Variable Maps § Map and location of minterms: Y 0 4 W 5 7 6 12 Variable Order 1 13 15 14 8 9 11 10 3 2 X Z Chapter 2 - Part 2 80

Four Variable Terms § Four variable maps can have rectangles corresponding to: • A single 1 = 4 variables, (i. e. Minterm) • Two 1 s = 3 variables, • Four 1 s = 2 variables • Eight 1 s = 1 variable, • Sixteen 1 s = zero variables (i. e. Constant "1") Chapter 2 - Part 2 81

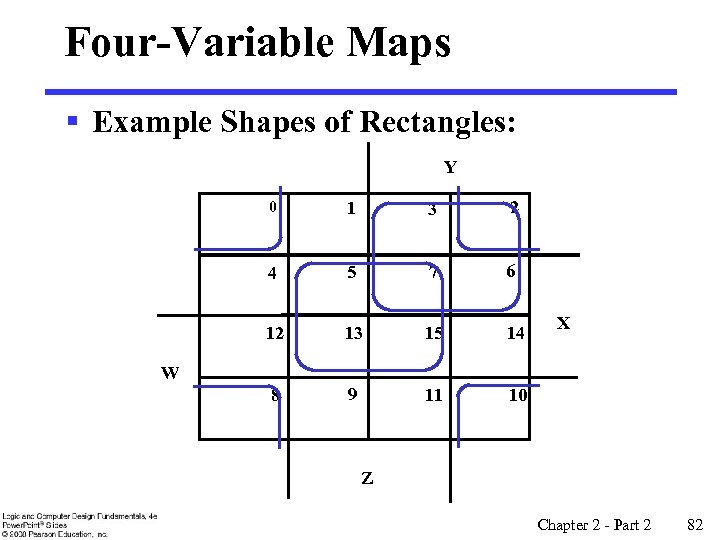Four-Variable Maps § Example Shapes of Rectangles: Y 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10 X W Z Chapter 2 - Part 2 82

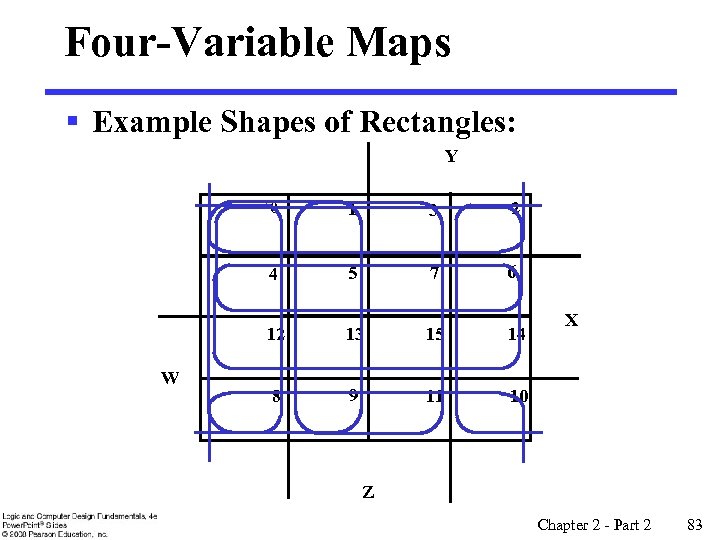Four-Variable Maps § Example Shapes of Rectangles: Y 0 3 2 4 5 7 6 12 W 1 13 15 14 8 9 11 10 X Z Chapter 2 - Part 2 83

Four-Variable Map Simplification § F(W, X, Y, Z) = S m (0, 2, 4, 5, 6, 7, 8, 10, 13, 15 ) Chapter 2 - Part 2 84

Four-Variable Map Simplification § F(W, X, Y, Z) = S m (3, 4, 5, 7, 9, 1 3, 14, 15 ) Chapter 2 - Part 2 85

Systematic Simplification § A Prime Implicant is a product term obtained by combining the maximum possible number of adjacent squares in the map into a rectangle with the number of squares a power of 2. § A prime implicant is called an Essential Prime Implicant if it is the only prime implicant that covers (includes) one or more minterms. § Prime Implicants and Essential Prime Implicants can be determined by inspection of a K-Map. § A set of prime implicants "covers all minterms" if, for each minterm of the function, at least one prime implicant in the set of prime implicants includes the minterm. Chapter 2 - Part 2 86

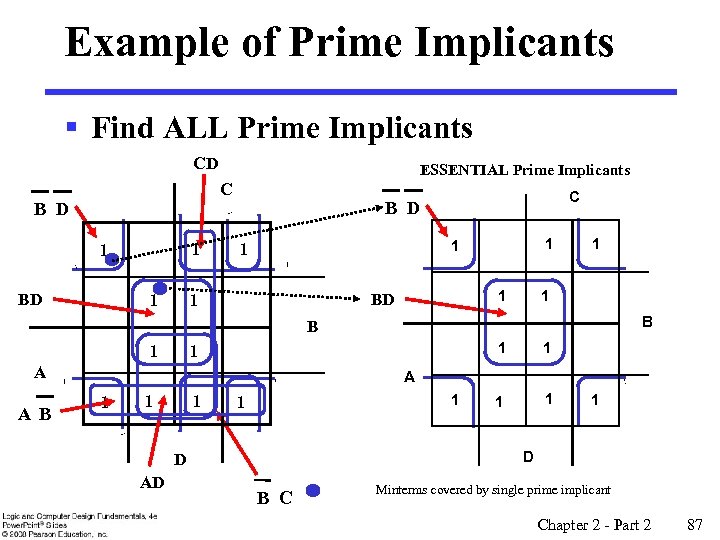Example of Prime Implicants § Find ALL Prime Implicants CD ESSENTIAL Prime Implicants C B D 1 1 BD 1 1 1 B B 1 1 1 A A B 1 1 1 A 1 1 1 D D AD 1 B C Minterms covered by single prime implicant Chapter 2 - Part 2 87

Prime Implicant Practice § Find all prime implicants for: Chapter 2 - Part 2 88

Another Example § Find all prime implicants for: • Hint: There are seven prime implicants! Chapter 2 - Part 2 89

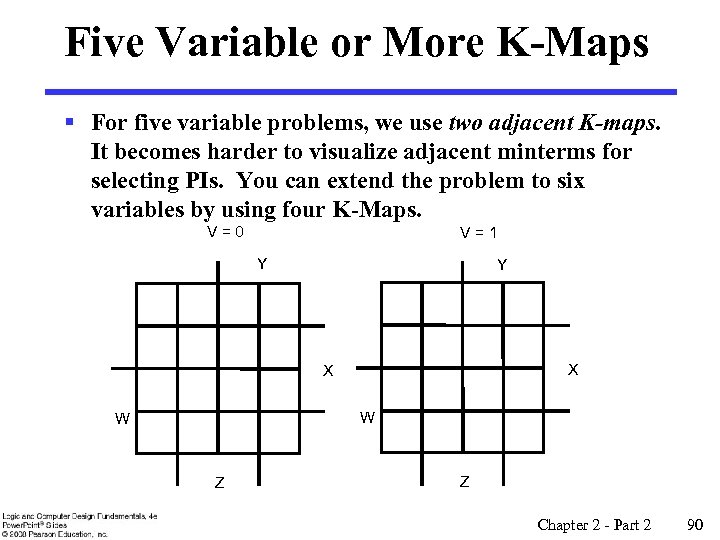Five Variable or More K-Maps § For five variable problems, we use two adjacent K-maps. It becomes harder to visualize adjacent minterms for selecting PIs. You can extend the problem to six variables by using four K-Maps. V=0 V=1 Y Y X X W W Z Z Chapter 2 - Part 2 90

Don't Cares in K-Maps § Sometimes a function table or map contains entries for which it is known: • the input values for the minterm will never occur, or • The output value for the minterm is not used § In these cases, the output value need not be defined § Instead, the output value is defined as a “don't care” § By placing “don't cares” ( an “x” entry) in the function table or map, the cost of the logic circuit may be lowered. § Example 1: A logic function having the binary codes for the BCD digits as its inputs. Only the codes for 0 through 9 are used. The six codes, 1010 through 1111 never occur, so the output values for these codes are “x” to represent “don’t cares. ” Chapter 2 - Part 2 91

Don't Cares in K-Maps § Example 2: A circuit that represents a very common situation that occurs in computer design has two distinct sets of input variables: • A, B, and C which take on all possible combinations, and • Y which takes on values 0 or 1. and a single output Z. The circuit that receives the output Z observes it only for combinations of A, B, and C such A = 1 and B = 1 or C = 0, otherwise ignoring it. Thus, Z is specified only for those combinations, and for all other combinations of A, B, and C, Z is a don’t care. Specifically, Z must be specified for AB + C = 1, and is a don’t care for : AB + C = (A + B)C = AC + BC = 1 § Ultimately, each don’t care “x” entry may take on either a 0 or 1 value in resulting solutions § For example, an “x” may take on value “ 0” in an SOP solution and value “ 1” in a POS solution, or vice-versa. § Any minterm with value “x” need not be covered by a prime implicant. Chapter 2 - Part 2 92

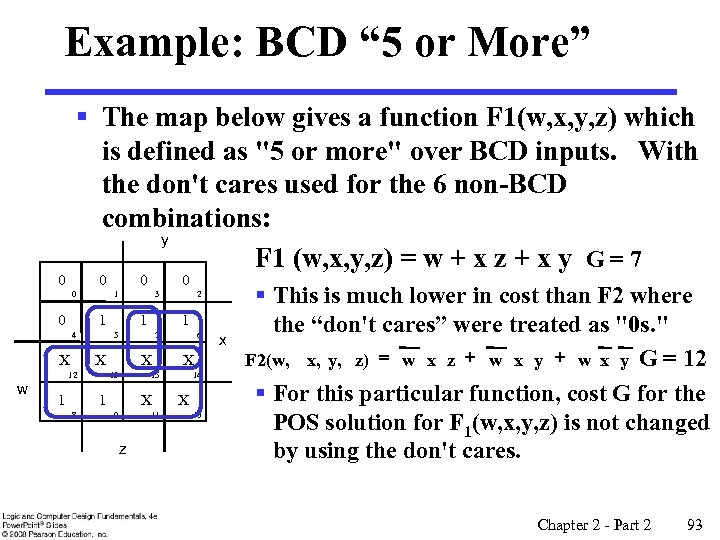Example: BCD “ 5 or More” § The map below gives a function F 1(w, x, y, z) which is defined as "5 or more" over BCD inputs. With the don't cares used for the 6 non-BCD combinations: y F 1 (w, x, y, z) = w + x z + x y G = 7 0 0 X 1 7 X X 13 6 X 15 1 8 2 1 5 12 1 0 3 1 4 w 0 1 X 9 11 z 14 X 10 x § This is much lower in cost than F 2 where the “don't cares” were treated as "0 s. " F 2(w, x, y, z) = w x z + w x y G = 12 § For this particular function, cost G for the POS solution for F 1(w, x, y, z) is not changed by using the don't cares. Chapter 2 - Part 2 93

Product of Sums Example § Find the optimum POS solution: • Hint: Use F and complement it to get the result. Chapter 2 - Part 2 94

Optimization Algorithm § Find all prime implicants. § Include all essential prime implicants in the solution § Select a minimum cost set of non-essential prime implicants to cover all minterms not yet covered: • Obtaining an optimum solution: See Reading Supplement - More on Optimization • Obtaining a good simplified solution: Use the Selection Rule Chapter 2 - Part 2 95

Prime Implicant Selection Rule § Minimize the overlap among prime implicants as much as possible. In particular, in the final solution, make sure that each prime implicant selected includes at least one minterm not included in any other prime implicant selected. Chapter 2 - Part 2 96

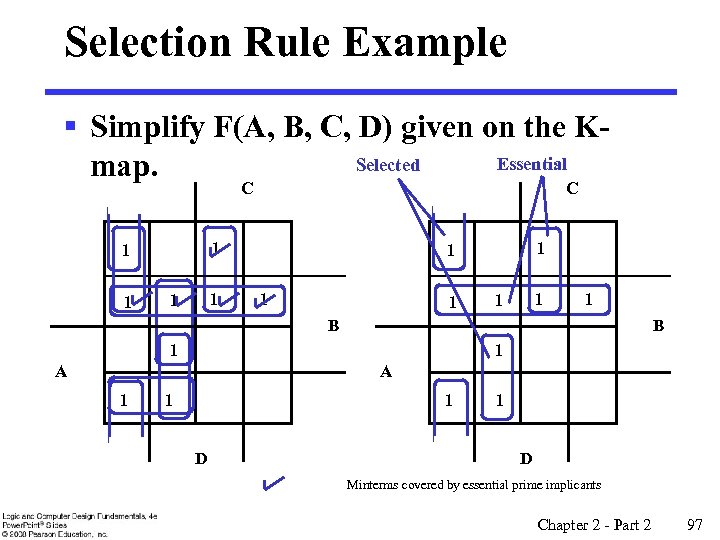Selection Rule Example § Simplify F(A, B, C, D) given on the KEssential Selected map. C 1 1 1 B B 1 1 A A 1 1 1 D Minterms covered by essential prime implicants Chapter 2 - Part 2 97

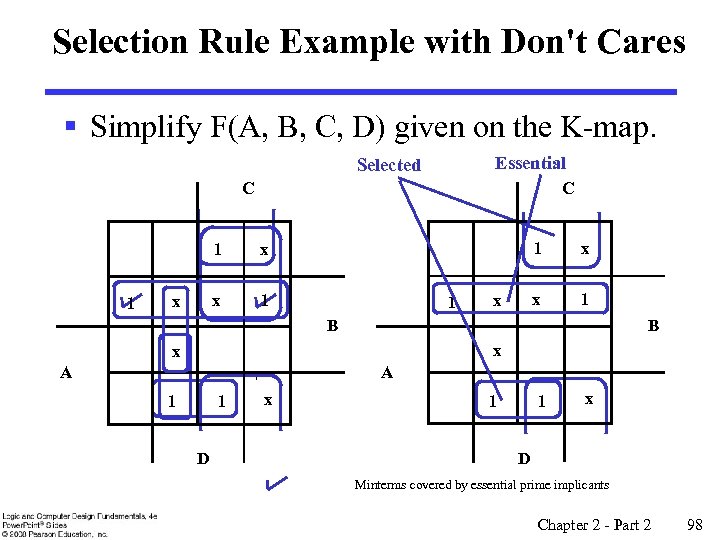Selection Rule Example with Don't Cares § Simplify F(A, B, C, D) given on the K-map. Essential Selected C C 1 1 x x 1 B B x x A A 1 1 D x 1 1 x D Minterms covered by essential prime implicants Chapter 2 - Part 2 98

Practical Optimization § Problem: Automated optimization algorithms: • require minterms as starting point, • require determination of all prime implicants, and/or • require a selection process with a potentially very large number of candidate solutions to be found. § Solution: Suboptimum algorithms not requiring any of the above in the general case Chapter 2 - Part 2 99

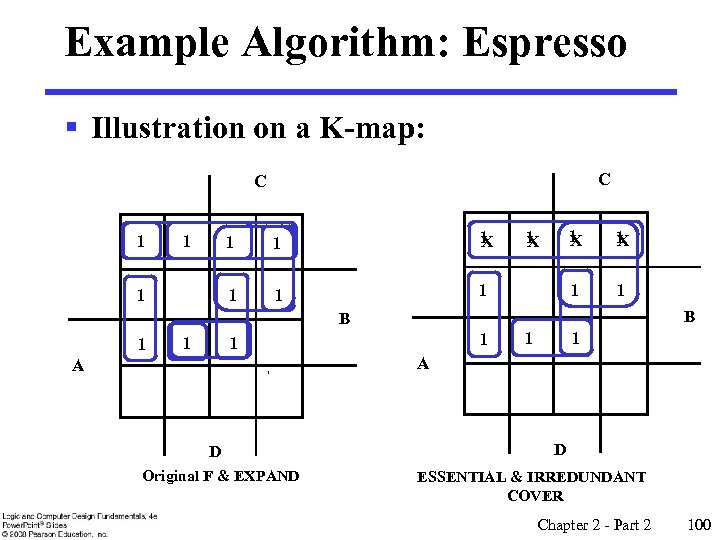Example Algorithm: Espresso § Illustration on a K-map: C C 1 1 1 X 1 1 X 1 B B 1 1 1 A A D Original F & EXPAND D ESSENTIAL & IRREDUNDANT COVER Chapter 2 - Part 2 100

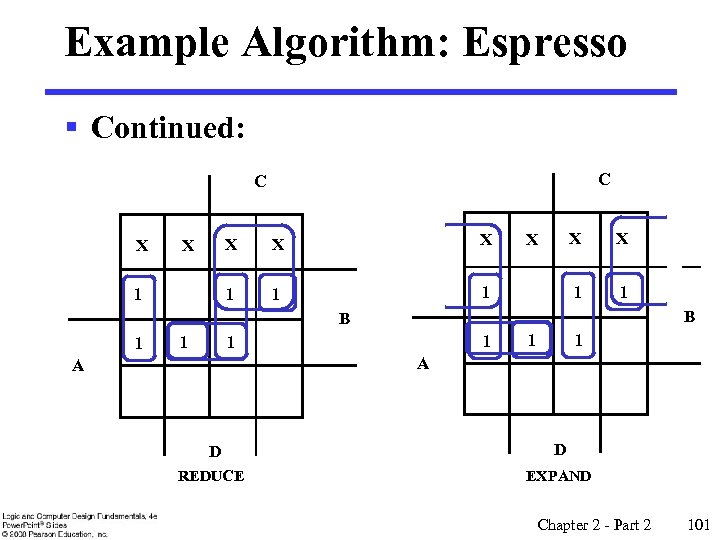Example Algorithm: Espresso § Continued: C C X X 1 X 1 X 1 B B 1 1 1 A A D D REDUCE EXPAND Chapter 2 - Part 2 101

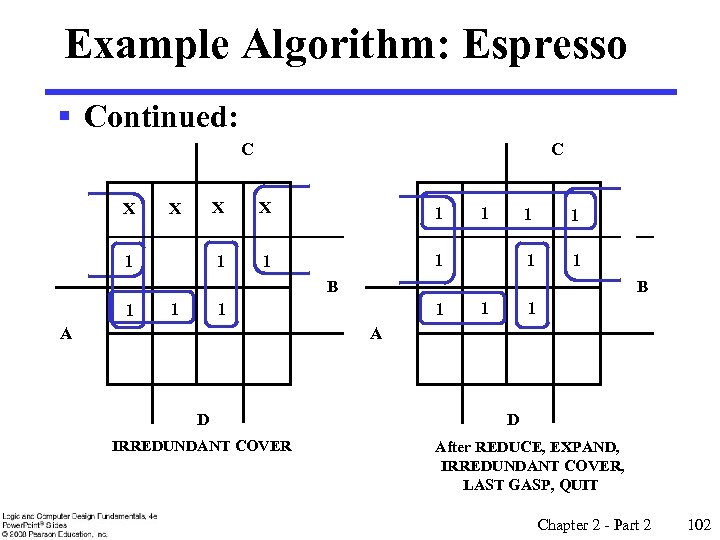Example Algorithm: Espresso § Continued: C X 1 X 1 1 1 1 B 1 A 1 1 1 A D IRREDUNDANT COVER D After REDUCE, EXPAND, IRREDUNDANT COVER, LAST GASP, QUIT Chapter 2 - Part 2 102

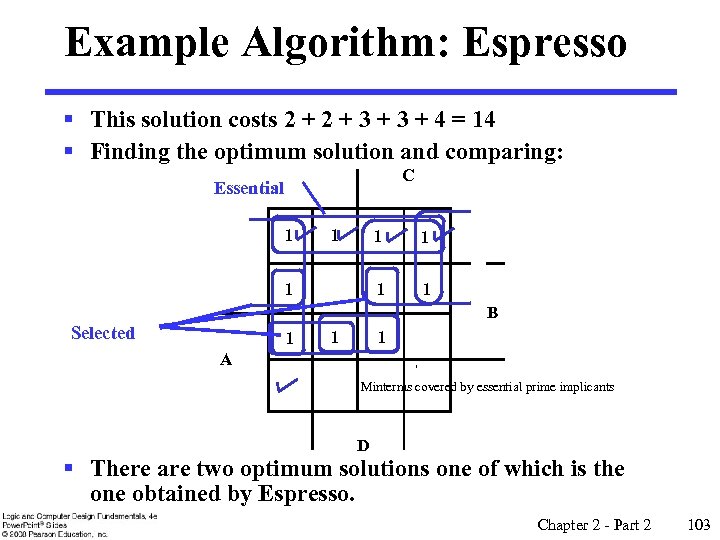Example Algorithm: Espresso § This solution costs 2 + 3 + 4 = 14 § Finding the optimum solution and comparing: C Essential 1 1 1 1 B Selected 1 1 1 A Minterms covered by essential prime implicants D § There are two optimum solutions one of which is the one obtained by Espresso. Chapter 2 - Part 2 103

Multiple-Level Optimization § Multiple-level circuits - circuits that are not two-level (with or without input and/or output inverters) § Multiple-level circuits can have reduced gate input cost compared to two-level (SOP and POS) circuits § Multiple-level optimization is performed by applying transformations to circuits represented by equations while evaluating cost Chapter 2 - Part 2 104

Transformations § Factoring - finding a factored form from SOP or POS expression • Algebraic - No use of axioms specific to Boolean algebra such as complements or idempotence • Boolean - Uses axioms unique to Boolean algebra § Decomposition - expression of a function as a set of new functions Chapter 2 - Part 2 105

Transformations (continued) § Substitution of G into F - expression function F as a function of G and some or all of its original variables § Elimination - Inverse of substitution § Extraction - decomposition applied to multiple functions simultaneously Chapter 2 - Part 2 106

Transformation Examples § Algebraic Factoring F = A C D + A B C + ABC + AC D G = 16 • Factoring: F = A ( C D + B C ) + A (BC + C D ) G = 16 • Factoring again: F = A C ( B + D ) + AC (B + D ) G = 12 • Factoring again: F = ( A C + AC) (B + D ) G = 10 Chapter 2 - Part 2 107

Transformation Examples § Decomposition • The terms B + D and A C + AC can be defined as new functions E and H respectively, decomposing F: F = E H, E = B + D , and H = A C + AC G = 10 § This series of transformations has reduced G from 16 to 10, a substantial savings. The resulting circuit has three levels plus input inverters. Chapter 2 - Part 2 108

Transformation Examples § Substitution of E into F • Returning to F just before the final factoring step: F = A C ( B + D ) + AC (B + D ) G = 12 • Defining E = B + D , and substituting in F: F = A C E + ACE G = 10 • This substitution has resulted in the same cost as the decomposition Chapter 2 - Part 2 109

Transformation Examples § Elimination • Beginning with a new set of functions: X=B+C Y=A+B Z=AX+CY G = 10 • Eliminating X and Y from Z: Z = A (B + C) + C (A + B) G = 10 • “Flattening” (Converting to SOP expression): Z = A B + A C + AC + BC G = 12 • This has increased the cost, but has provided an new SOP expression for two-level optimization. Chapter 2 - Part 2 110

Transformation Examples § Two-level Optimization • The result of 2 -level optimization is: Z= A B+ C G=4 § This example illustrates that: • Optimization can begin with any set of equations, not just with minterms or a truth table • Increasing gate input count G temporarily during a series of transformations can result in a final solution with a smaller G Chapter 2 - Part 2 111

Transformation Examples § Extraction • Beginning with two functions: E = A B D + A BD H = B C D + BCD G = 16 • Finding a common factor and defining it as a function: F = B D + BD • We perform extraction by expressing E and H as the three functions: F = B D + BD, E = A F, H = CF G = 10 • The reduced cost G results from the sharing of logic between the two output functions Chapter 2 - Part 2 112

Other Gate Types § Why? • Implementation feasibility and low cost • Power in implementing Boolean functions • Convenient conceptual representation § Gate classifications • Primitive gate - a gate that can be described using a single primitive operation type (AND or OR) plus an optional inversion(s). • Complex gate - a gate that requires more than one primitive operation type for its description § Primitive gates will be covered first Chapter 2 - Part 3 113

Buffer § A buffer is a gate with the function F = X: X F § In terms of Boolean function, a buffer is the same as a connection! § So why use it? • A buffer is an electronic amplifier used to improve circuit voltage levels and increase the speed of circuit operation. Chapter 2 - Part 3 114

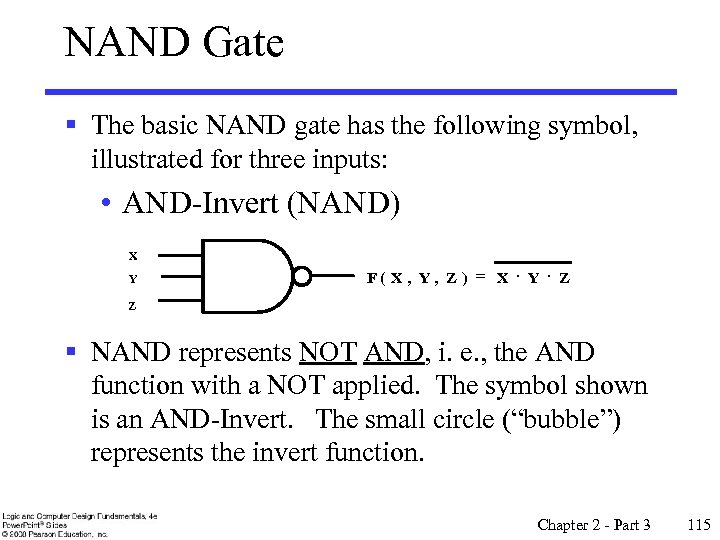NAND Gate § The basic NAND gate has the following symbol, illustrated for three inputs: • AND-Invert (NAND) X Y F( X, Y, Z) = X Y Z Z § NAND represents NOT AND, i. e. , the AND function with a NOT applied. The symbol shown is an AND-Invert. The small circle (“bubble”) represents the invert function. Chapter 2 - Part 3 115

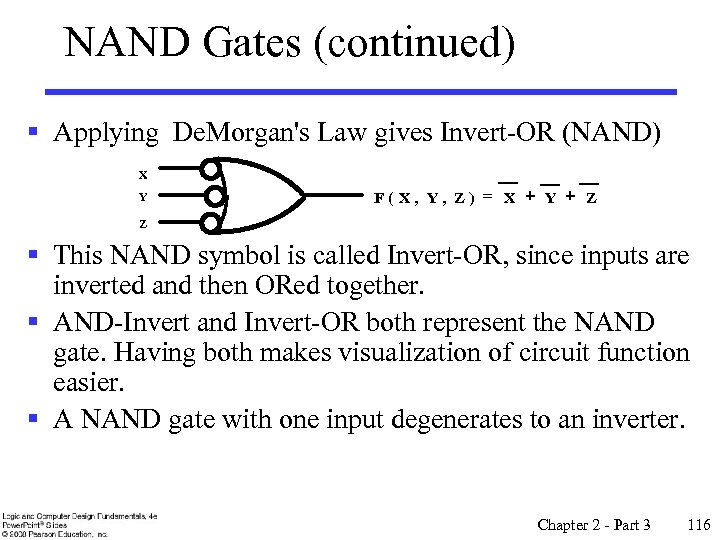NAND Gates (continued) § Applying De. Morgan's Law gives Invert-OR (NAND) X Y F( X, Y, Z) = X + Y + Z Z § This NAND symbol is called Invert-OR, since inputs are inverted and then ORed together. § AND-Invert and Invert-OR both represent the NAND gate. Having both makes visualization of circuit function easier. § A NAND gate with one input degenerates to an inverter. Chapter 2 - Part 3 116

NAND Gates (continued) § The NAND gate is the natural implementation for CMOS technology in terms of chip area and speed. § Universal gate - a gate type that can implement any Boolean function. § The NAND gate is a universal gate as shown in Figure 224 of the text. § NAND usually does not have a operation symbol defined since • the NAND operation is not associative, and • we have difficulty dealing with non-associative mathematics! Chapter 2 - Part 3 117

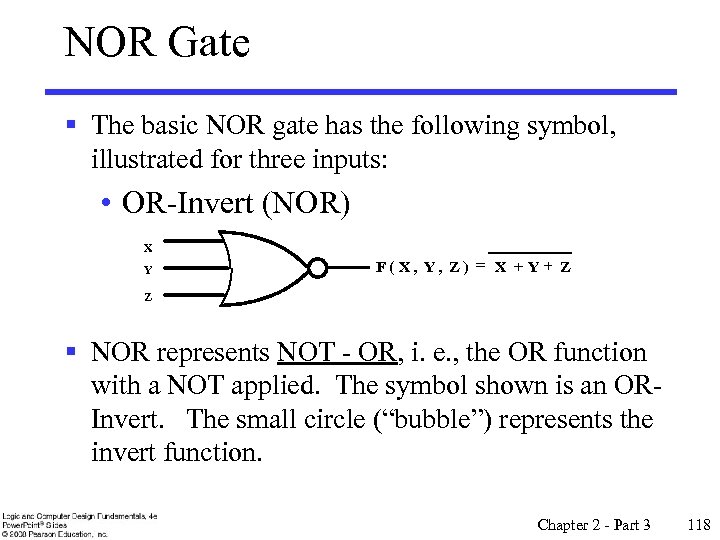NOR Gate § The basic NOR gate has the following symbol, illustrated for three inputs: • OR-Invert (NOR) X Y F( X, Y, Z ) = X + Y + Z Z § NOR represents NOT - OR, i. e. , the OR function with a NOT applied. The symbol shown is an ORInvert. The small circle (“bubble”) represents the invert function. Chapter 2 - Part 3 118

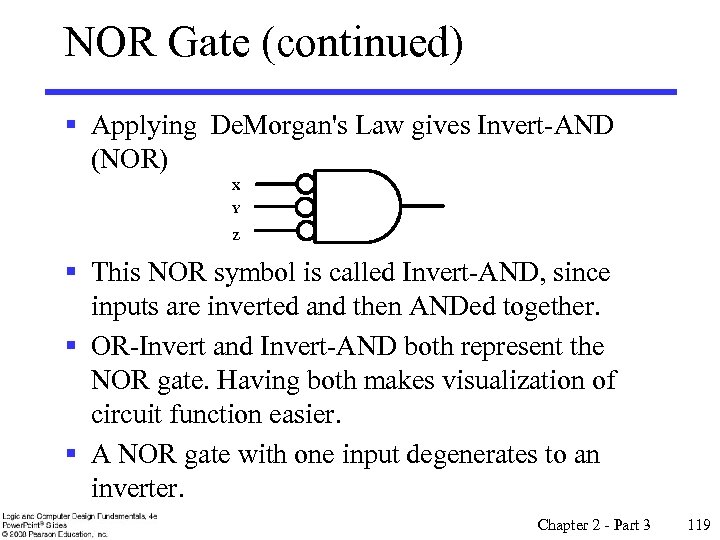NOR Gate (continued) § Applying De. Morgan's Law gives Invert-AND (NOR) X Y Z § This NOR symbol is called Invert-AND, since inputs are inverted and then ANDed together. § OR-Invert and Invert-AND both represent the NOR gate. Having both makes visualization of circuit function easier. § A NOR gate with one input degenerates to an inverter. Chapter 2 - Part 3 119

NOR Gate (continued) § The NOR gate is a natural implementation for some technologies other than CMOS in terms of chip area and speed. § The NOR gate is a universal gate § NOR usually does not have a defined operation symbol since • the NOR operation is not associative, and • we have difficulty dealing with non-associative mathematics! Chapter 2 - Part 3 120

Exclusive OR/ Exclusive NOR § The e. Xclusive OR (XOR) function is an important Boolean function used extensively in logic circuits. § The XOR function may be; • implemented directly as an electronic circuit (truly a gate) or • implemented by interconnecting other gate types (used as a convenient representation) § The e. Xclusive NOR function is the complement of the XOR function § By our definition, XOR and XNOR gates are complex gates. Chapter 2 - Part 3 121

Exclusive OR/ Exclusive NOR § Uses for the XOR and XNORs gate include: • Adders/subtractors/multipliers • Counters/incrementers/decrementers • Parity generators/checkers § Definitions • The XOR function is: X Å Y = X Y + X Y • The e. Xclusive NOR (XNOR) function, otherwise known as equivalence is: X Å Y = X Y + X Y § Strictly speaking, XOR and XNOR gates do no exist for more that two inputs. Instead, they are replaced by odd and even functions. Chapter 2 - Part 3 122

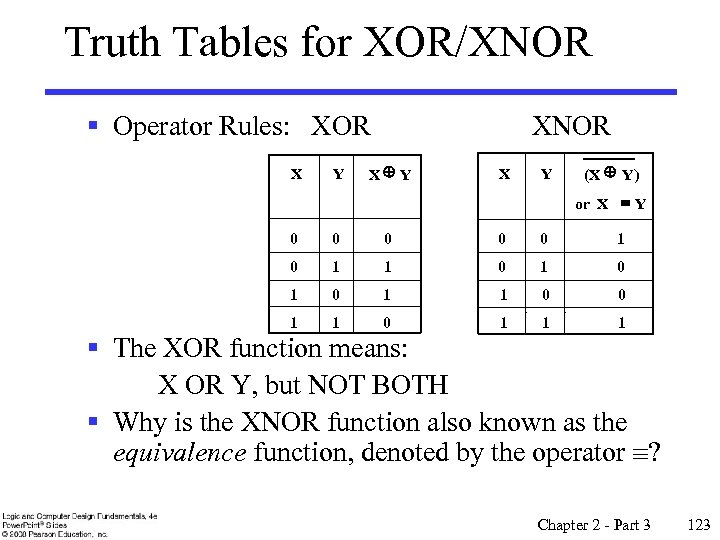Truth Tables for XOR/XNOR § Operator Rules: XOR XNOR X Y XÅ Y X Y (X Å Y) or X º Y 0 0 0 1 1 0 1 1 1 § The XOR function means: X OR Y, but NOT BOTH § Why is the XNOR function also known as the equivalence function, denoted by the operator ? Chapter 2 - Part 3 123

XOR/XNOR (Continued) § The XOR function can be extended to 3 or more variables. For more than 2 variables, it is called an odd function or modulo 2 sum (Mod 2 sum), not an XOR: X Å Y Å Z = X Y Z + X Y Z § The complement of the odd function is the even function. § The XOR identities: X Å 0 = X X Å 1 = X X Å X = 0 X Å X = 1 X Å Y = Y Å X (X Å Y) Å Z = X Å (Y Å Z) = X Å Y Å Z Chapter 2 - Part 3 124

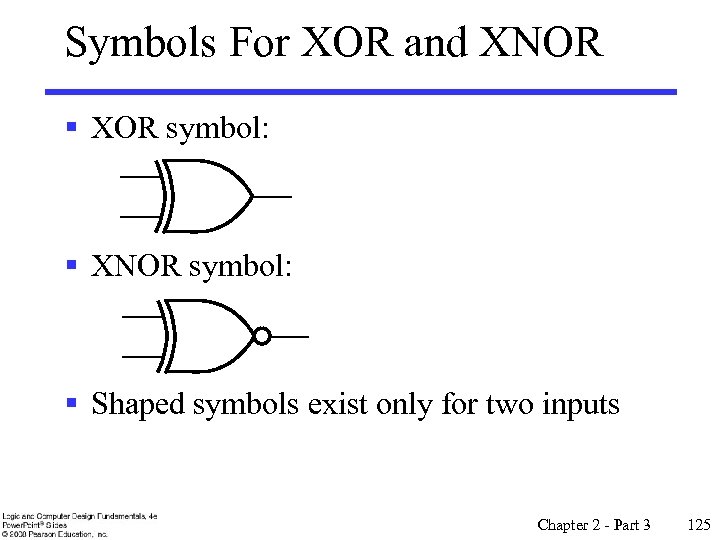Symbols For XOR and XNOR § XOR symbol: § XNOR symbol: § Shaped symbols exist only for two inputs Chapter 2 - Part 3 125

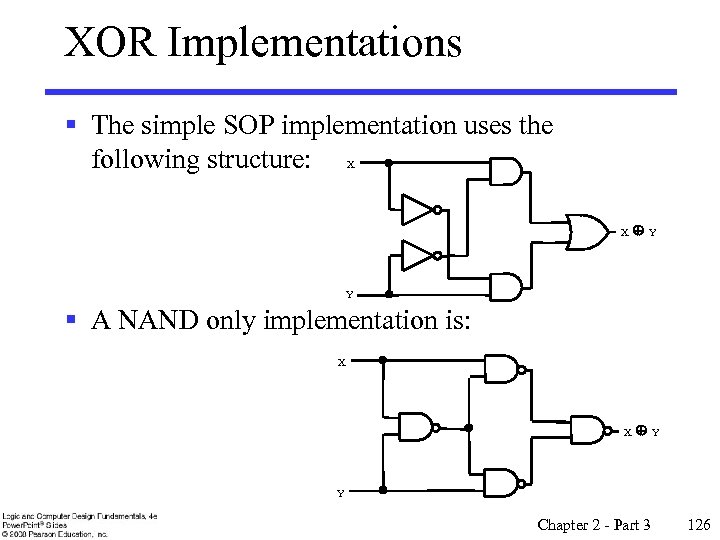XOR Implementations § The simple SOP implementation uses the following structure: X X Y Y § A NAND only implementation is: X X Y Y Chapter 2 - Part 3 126

Odd and Even Functions § The odd and even functions on a K-map form “checkerboard” patterns. § The 1 s of an odd function correspond to minterms having an index with an odd number of 1 s. § The 1 s of an even function correspond to minterms having an index with an even number of 1 s. § Implementation of odd and even functions for greater than four variables as a two-level circuit is difficult, so we use “trees” made up of : • 2 -input XOR or XNORs • 3 - or 4 -input odd or even functions Chapter 2 - Part 3 127

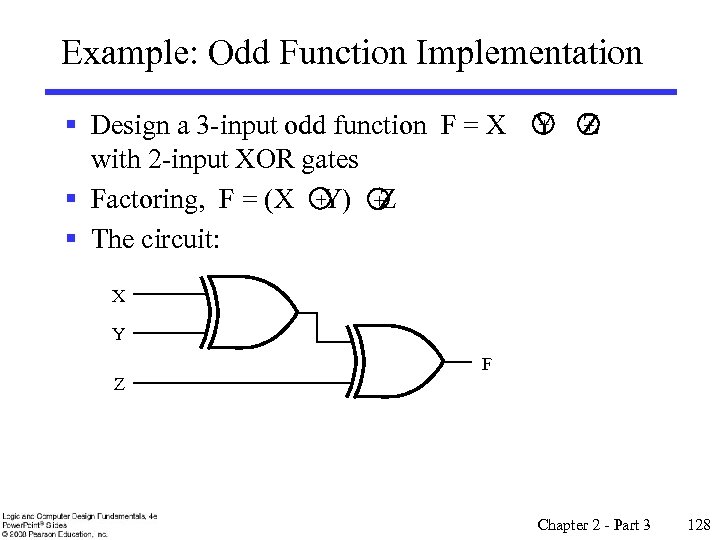Example: Odd Function Implementation + + § Design a 3 -input odd function F = X Y Z with 2 -input XOR gates + + § Factoring, F = (X Y) Z § The circuit: X Y Z F Chapter 2 - Part 3 128

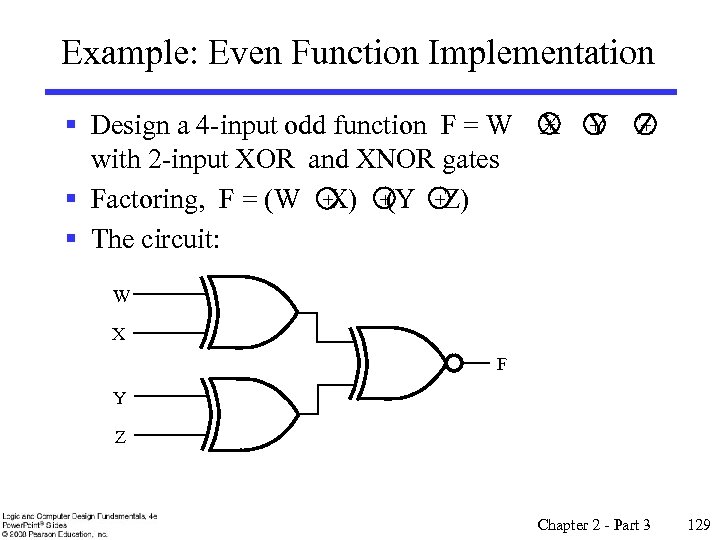Example: Even Function Implementation + + + § Design a 4 -input odd function F = W X Y Z with 2 -input XOR and XNOR gates + + + § Factoring, F = (W X) (Y Z) § The circuit: W X F Y Z Chapter 2 - Part 3 129

Parity Generators and Checkers § In Chapter 1, a parity bit added to n-bit code to produce an n + 1 bit code: • • Add odd parity bit to generate code words with even parity Add even parity bit to generate code words with odd parity Use odd parity circuit to check code words with even parity Use even parity circuit to check code words with odd parity § Example: n = 3. Generate even X parity code words of length four Y with odd parity generator: Z § Check even parity code words of X length four with odd parity checker: Y § Operation: (X, Y, Z) = (0, 0, 1) gives Z (X, Y, Z, P) = (0, 0, 1, 1) and E = 0. P If Y changes from 0 to 1 between generator and checker, then E = 1 indicates an error. P E Chapter 2 - Part 3 130

Hi-Impedance Outputs § Logic gates introduced thus far • have 1 and 0 output values, • cannot have their outputs connected together, and • transmit signals on connections in only one direction. § Three-state logic adds a third logic value, Hi. Impedance (Hi-Z), giving three states: 0, 1, and Hi-Z on the outputs. § The presence of a Hi-Z state makes a gate output as described above behave quite differently: • “ 1 and 0” become “ 1, 0, and Hi-Z” • “cannot” becomes “can, ” and • “only one” becomes “two” Chapter 2 - Part 3 131

Hi-Impedance Outputs (continued) § What is a Hi-Z value? • • • § The Hi-Z value behaves as an open circuit This means that, looking back into the circuit, the output appears to be disconnected. It is as if a switch between the internal circuitry and the output has been opened. Hi-Z may appear on the output of any gate, but we restrict gates to: • • a 3 -state buffer, or Optional: a transmission gate (See Reading Supplement: More on CMOS Circuit-Level Design), each of which has one data input and one control input. Chapter 2 - Part 3 132

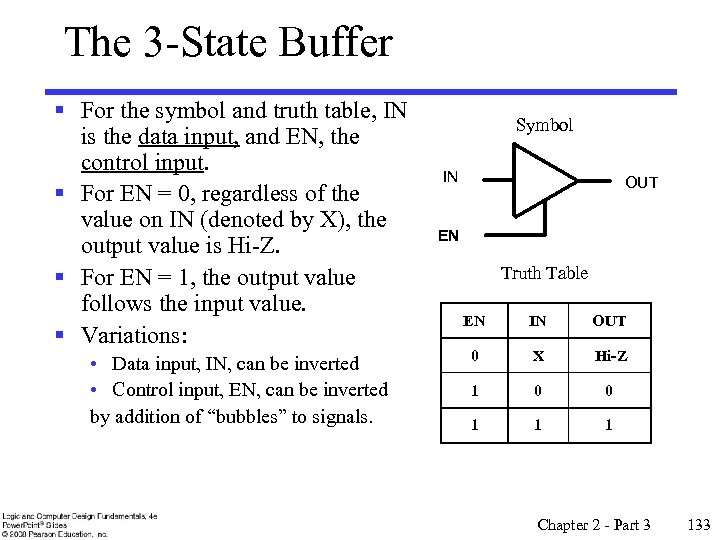The 3 -State Buffer § For the symbol and truth table, IN is the data input, and EN, the control input. § For EN = 0, regardless of the value on IN (denoted by X), the output value is Hi-Z. § For EN = 1, the output value follows the input value. § Variations: • Data input, IN, can be inverted • Control input, EN, can be inverted by addition of “bubbles” to signals. Symbol IN OUT EN Truth Table EN IN OUT 0 X Hi-Z 1 0 0 1 1 1 Chapter 2 - Part 3 133

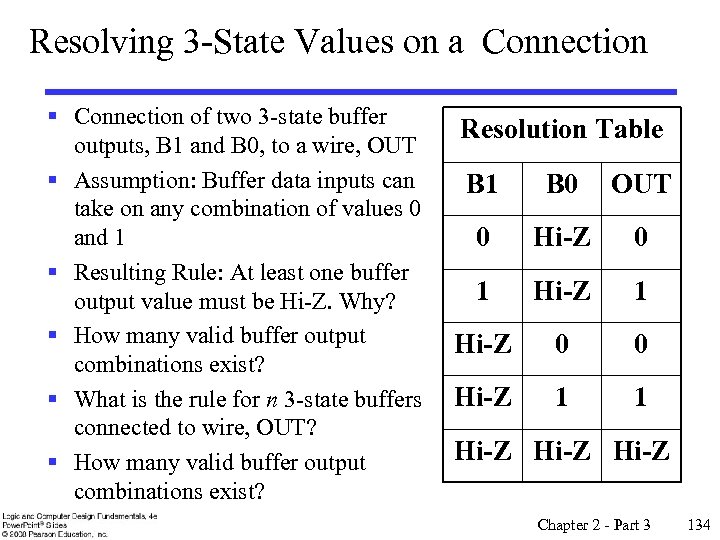Resolving 3 -State Values on a Connection § Connection of two 3 -state buffer outputs, B 1 and B 0, to a wire, OUT § Assumption: Buffer data inputs can take on any combination of values 0 and 1 § Resulting Rule: At least one buffer output value must be Hi-Z. Why? § How many valid buffer output combinations exist? § What is the rule for n 3 -state buffers connected to wire, OUT? § How many valid buffer output combinations exist? Resolution Table B 1 B 0 OUT 0 Hi-Z 0 1 Hi-Z 0 0 Hi-Z 1 1 Hi-Z Chapter 2 - Part 3 134

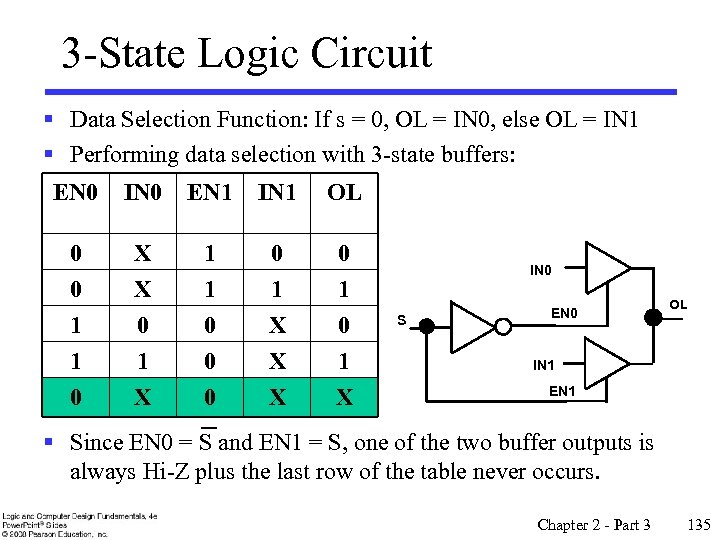3 -State Logic Circuit § Data Selection Function: If s = 0, OL = IN 0, else OL = IN 1 § Performing data selection with 3 -state buffers: EN 0 IN 0 EN 1 IN 1 OL 0 0 X X 1 1 0 1 1 1 0 0 1 X 0 0 0 X X X 0 1 X IN 0 S EN 0 OL IN 1 EN 1 § Since EN 0 = S and EN 1 = S, one of the two buffer outputs is always Hi-Z plus the last row of the table never occurs. Chapter 2 - Part 3 135

More Complex Gates § The remaining complex gates are SOP or POS structures with and without an output inverter. § The names are derived using: • • A - AND O - OR I - Inverter Numbers of inputs on first-level “gates” or directly to second-level “gates” Chapter 2 - Part 3 136

More Complex Gates (continued) § Example: AOI - AND-OR-Invert consists of a single gate with AND functions driving an OR function which is inverted. § Example: 2 -2 -1 AO has two 2 -input ANDS driving an OR with one additional OR input § These gate types are used because: • the number of transistors needed is fewer than required by connecting together primitive gates • potentially, the circuit delay is smaller, increasing the circuit operating speed Chapter 2 - Part 3 137

Terms of Use § All (or portions) of this material © 2008 by Pearson Education, Inc. § Permission is given to incorporate this material or adaptations thereof into classroom presentations and handouts to instructors in courses adopting the latest edition of Logic and Computer Design Fundamentals as the course textbook. § These materials or adaptations thereof are not to be sold or otherwise offered for consideration. § This Terms of Use slide or page is to be included within the original materials or any adaptations thereof. Chapter 2 - Part 1 138