Логарифмическая функция и ее свойства 49 стр

Логарифмическая функция и ее свойства. § 49, стр. 264

Повторение пройденного • Дать определение логарифма числа: • Записать общий вид показательной функции: • Перечислить свойства показательной функции при а>1 и при 0<а<1. • Как называется график показательной функции?

Рассмотрим функции: у= ах и у=logах. Пусть точка (в, с) принадлежит графику функции у= ах тогда, с= ав или b=logас, следовательно если, точка (в, с) принадлежит графику функции у= ах , то точка (с; в) принадлежит графику функции у=logах. • Вывод: график функции у=logах симметричен графику функции у= ах относительно прямой у=х. Определение. • Функцию вида у=logах (где а, х>0, а≠ 1) называют логарифмической функцией. • График функции у=logах называют логарифмической кривой или экспонентой.

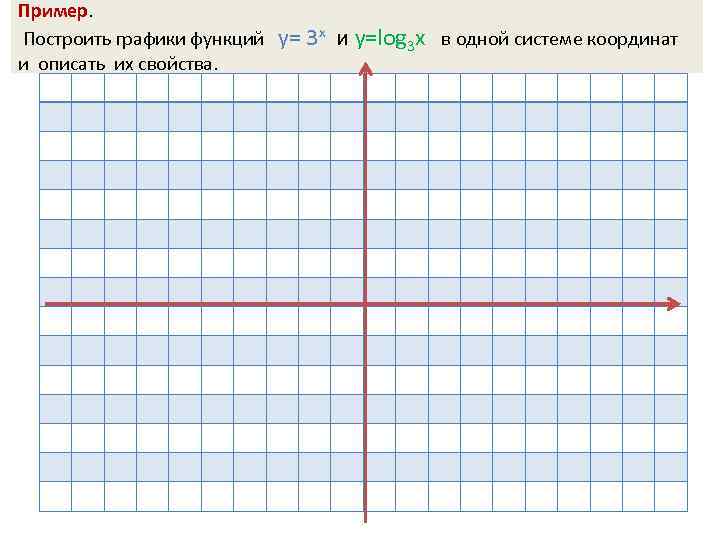Пример. Построить графики функций и описать их свойства. у= 3 х и у=log 3 х в одной системе координат

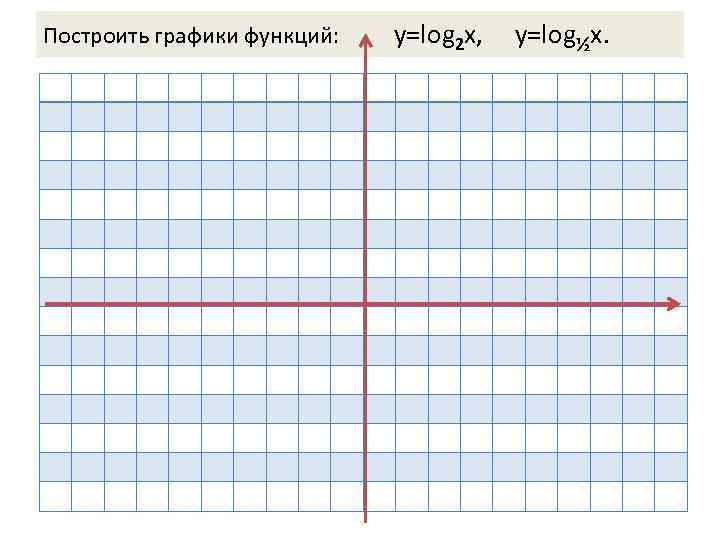Построить графики функций: у=log 2 х, у=log½х.

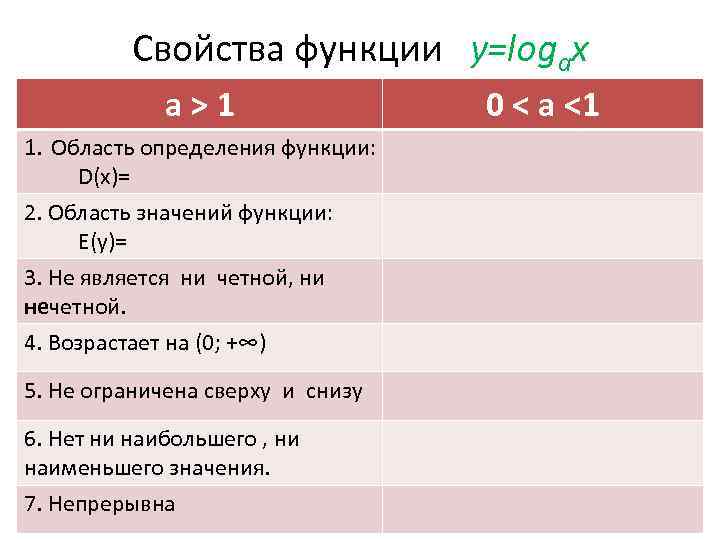Свойства функции у=logах а>1 1. Область определения функции: D(х)= 2. Область значений функции: Е(у)= 3. Не является ни четной, ни нечетной. 4. Возрастает на (0; +∞) 5. Не ограничена сверху и снизу 6. Нет ни наибольшего , ни наименьшего значения. 7. Непрерывна 0 < а <1

Задание: найти значение аргумента, если известно значение функции : а) у=log¼х, у=2 Решение. • б) у=log¾х , у= -2 Решение.

Экзаменационное задание (стр. 151) Найти область определения функции: Решение.

Экзаменационное задание (стр. 160, вариант № 95) Найти область определения функции: Решение.

Экзаменационное задание (стр. 91) Найти область определения функции: Решение.

Самостоятельная работа. • Вариант № 1 1. Найти значение аргумента х для функции у= log 3(2 х-5), если у=2. • Вариант № 2 1. Найти значение аргумента х для функции у= log 3(2 -5 х), если у=-2. 2. Найти область определения функции: (в-94, стр. 158) 2. Найти область определения функции: (в-90, стр. 151)

Домашнее задание. • § 49, стр. 264, • Выучить определение логарифмической функции, • Построить график функции: у=log 0, 5 х и найти его наименьшее и наибольшее значение.