0b5b281e05e737af26d714cfb9ff8e45.ppt
- Количество слайдов: 40
 LO 1 Multiple Cash Flows 6. 1 – FV Example 1 • You currently have $7, 000 in a bank account earning 8% interest. You think you will be able to deposit an additional $4, 000 at the end of each of the next three years. How much will you have in three years? © 2013 Mc. Graw-Hill Ryerson Limited 6 -0
LO 1 Multiple Cash Flows 6. 1 – FV Example 1 • You currently have $7, 000 in a bank account earning 8% interest. You think you will be able to deposit an additional $4, 000 at the end of each of the next three years. How much will you have in three years? © 2013 Mc. Graw-Hill Ryerson Limited 6 -0
 LO 1 Multiple Cash Flows FV Example 1 continued • Find the value at year 3 of each cash flow and add them together. • Formula Approach • • • Today (year 0): FV = 7000(1. 08)3 = 8, 817. 98 Year 1: FV = 4, 000(1. 08)2 = 4, 665. 60 Year 2: FV = 4, 000(1. 08) = 4, 320 Year 3: value = 4, 000 Total value in 3 years = 8817. 98 + 4665. 60 + 4320 + 4000 = 21, 803. 58 © 2013 Mc. Graw-Hill Ryerson Limited 6 -1
LO 1 Multiple Cash Flows FV Example 1 continued • Find the value at year 3 of each cash flow and add them together. • Formula Approach • • • Today (year 0): FV = 7000(1. 08)3 = 8, 817. 98 Year 1: FV = 4, 000(1. 08)2 = 4, 665. 60 Year 2: FV = 4, 000(1. 08) = 4, 320 Year 3: value = 4, 000 Total value in 3 years = 8817. 98 + 4665. 60 + 4320 + 4000 = 21, 803. 58 © 2013 Mc. Graw-Hill Ryerson Limited 6 -1
 LO 1 Multiple Cash Flows FV Example 1 continued • Calculator Approach • Today (year 0 CF): 3 N; 8 I/Y; -7000 PV; CPT FV = 8817. 98 • Year 1 CF: 2 N; 8 I/Y; -4000 PV; CPT FV = 4665. 60 • Year 2 CF: 1 N; 8 I/Y; -4000 PV; CPT FV = 4320 • Year 3 CF: value = 4, 000 • Total value in 3 years = 8817. 98 + 4665. 60 + 4320 + 4000 = 21, 803. 58 © 2013 Mc. Graw-Hill Ryerson Limited 6 -2
LO 1 Multiple Cash Flows FV Example 1 continued • Calculator Approach • Today (year 0 CF): 3 N; 8 I/Y; -7000 PV; CPT FV = 8817. 98 • Year 1 CF: 2 N; 8 I/Y; -4000 PV; CPT FV = 4665. 60 • Year 2 CF: 1 N; 8 I/Y; -4000 PV; CPT FV = 4320 • Year 3 CF: value = 4, 000 • Total value in 3 years = 8817. 98 + 4665. 60 + 4320 + 4000 = 21, 803. 58 © 2013 Mc. Graw-Hill Ryerson Limited 6 -2
 LO 1 Multiple Cash Flows – FV Example 2 • Suppose you invest $500 in a mutual fund today and $600 in one year. If the fund pays 9% annually, how much will you have in two years? • Formula Approach • FV = 500(1. 09)2 + 600(1. 09) = 1248. 05 • Calculator Approach • Year 0 CF: 2 N; -500 PV; 9 I/Y; CPT FV = 594. 05 • Year 1 CF: 1 N; -600 PV; 9 I/Y; CPT FV = 654. 00 • Total FV = 594. 05 + 654. 00 = 1248. 05 © 2013 Mc. Graw-Hill Ryerson Limited 6 -3
LO 1 Multiple Cash Flows – FV Example 2 • Suppose you invest $500 in a mutual fund today and $600 in one year. If the fund pays 9% annually, how much will you have in two years? • Formula Approach • FV = 500(1. 09)2 + 600(1. 09) = 1248. 05 • Calculator Approach • Year 0 CF: 2 N; -500 PV; 9 I/Y; CPT FV = 594. 05 • Year 1 CF: 1 N; -600 PV; 9 I/Y; CPT FV = 654. 00 • Total FV = 594. 05 + 654. 00 = 1248. 05 © 2013 Mc. Graw-Hill Ryerson Limited 6 -3
 LO 1 Multiple Cash Flows – FV Example 2 Continued • How much will you have in 5 years if you make no further deposits? • Formula Approach • First way: • FV = 500(1. 09)5 + 600(1. 09)4 = 1616. 26 • Second way – use value at year 2: • FV = 1248. 05(1. 09)3 = 1616. 26 • Calculator Approach • First way: • Year 0 CF: 5 N; -500 PV; 9 I/Y; CPT FV = 769. 31 • Year 1 CF: 4 N; -600 PV; 9 I/Y; CPT FV = 846. 95 • Total FV = 769. 31 + 846. 95 = 1616. 26 • Second way – use value at year 2: • 3 N; -1248. 05 PV; 9 I/Y; CPT FV = 1616. 26 © 2013 Mc. Graw-Hill Ryerson Limited 6 -4
LO 1 Multiple Cash Flows – FV Example 2 Continued • How much will you have in 5 years if you make no further deposits? • Formula Approach • First way: • FV = 500(1. 09)5 + 600(1. 09)4 = 1616. 26 • Second way – use value at year 2: • FV = 1248. 05(1. 09)3 = 1616. 26 • Calculator Approach • First way: • Year 0 CF: 5 N; -500 PV; 9 I/Y; CPT FV = 769. 31 • Year 1 CF: 4 N; -600 PV; 9 I/Y; CPT FV = 846. 95 • Total FV = 769. 31 + 846. 95 = 1616. 26 • Second way – use value at year 2: • 3 N; -1248. 05 PV; 9 I/Y; CPT FV = 1616. 26 © 2013 Mc. Graw-Hill Ryerson Limited 6 -4
 LO 1 Multiple Cash Flows – FV Example 3 • Suppose you plan to deposit $100 into an account in one year and $300 into the account in three years. How much will be in the account in five years if the interest rate is 8%? • Formula Approach • FV = 100(1. 08)4 + 300(1. 08)2 = 136. 05 + 349. 92 = 485. 97 • Calculator Approach • Year 1 CF: 4 N; -100 PV; 8 I/Y; CPT FV = 136. 05 • Year 3 CF: 2 N; -300 PV; 8 I/Y; CPT FV = 349. 92 • Total FV = 136. 05 + 349. 92 = 485. 97 © 2013 Mc. Graw-Hill Ryerson Limited 6 -5
LO 1 Multiple Cash Flows – FV Example 3 • Suppose you plan to deposit $100 into an account in one year and $300 into the account in three years. How much will be in the account in five years if the interest rate is 8%? • Formula Approach • FV = 100(1. 08)4 + 300(1. 08)2 = 136. 05 + 349. 92 = 485. 97 • Calculator Approach • Year 1 CF: 4 N; -100 PV; 8 I/Y; CPT FV = 136. 05 • Year 3 CF: 2 N; -300 PV; 8 I/Y; CPT FV = 349. 92 • Total FV = 136. 05 + 349. 92 = 485. 97 © 2013 Mc. Graw-Hill Ryerson Limited 6 -5
 LO 1 Multiple Cash Flows – PV Example 1 • You are offered an investment that will pay you $200 in one year, $400 the next year, $600 the year after, and $800 at the end of the following year. You can earn 12% on similar investments. How much is this investment worth today? © 2013 Mc. Graw-Hill Ryerson Limited 6 -6
LO 1 Multiple Cash Flows – PV Example 1 • You are offered an investment that will pay you $200 in one year, $400 the next year, $600 the year after, and $800 at the end of the following year. You can earn 12% on similar investments. How much is this investment worth today? © 2013 Mc. Graw-Hill Ryerson Limited 6 -6
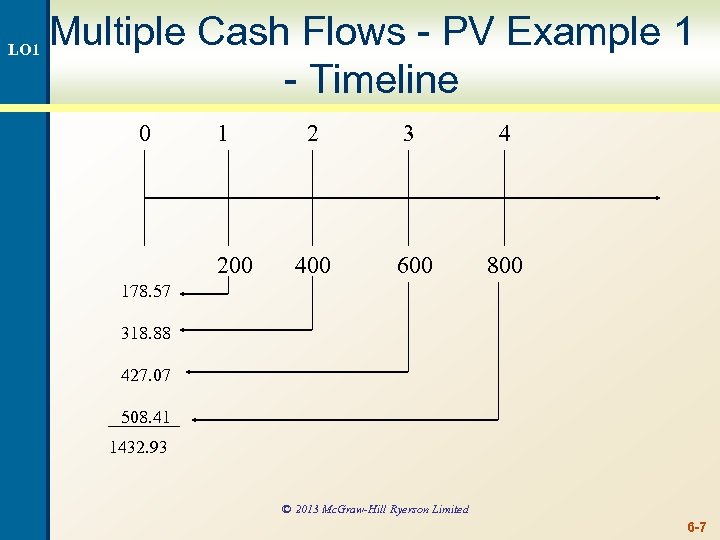 LO 1 Multiple Cash Flows - PV Example 1 - Timeline 0 1 200 2 3 4 400 600 800 178. 57 318. 88 427. 07 508. 41 1432. 93 © 2013 Mc. Graw-Hill Ryerson Limited 6 -7
LO 1 Multiple Cash Flows - PV Example 1 - Timeline 0 1 200 2 3 4 400 600 800 178. 57 318. 88 427. 07 508. 41 1432. 93 © 2013 Mc. Graw-Hill Ryerson Limited 6 -7
 LO 1 Multiple Cash Flows - PV Example 1 continued • Find the PV of each cash flow and add them • Formula Approach • • • Year 1 CF: 200 / (1. 12)1 = 178. 57 Year 2 CF: 400 / (1. 12)2 = 318. 88 Year 3 CF: 600 / (1. 12)3 = 427. 07 Year 4 CF: 800 / (1. 12)4 = 508. 41 Total PV = 178. 57 + 318. 88 + 427. 07 + 508. 41 = 1432. 93 © 2013 Mc. Graw-Hill Ryerson Limited 6 -8
LO 1 Multiple Cash Flows - PV Example 1 continued • Find the PV of each cash flow and add them • Formula Approach • • • Year 1 CF: 200 / (1. 12)1 = 178. 57 Year 2 CF: 400 / (1. 12)2 = 318. 88 Year 3 CF: 600 / (1. 12)3 = 427. 07 Year 4 CF: 800 / (1. 12)4 = 508. 41 Total PV = 178. 57 + 318. 88 + 427. 07 + 508. 41 = 1432. 93 © 2013 Mc. Graw-Hill Ryerson Limited 6 -8
 LO 1 Multiple Cash Flows - PV Example 1 continued • Calculator Approach • Year 1 CF: N = 1; I/Y = 12; FV = 200; CPT PV = 178. 57 • Year 2 CF: N = 2; I/Y = 12; FV = 400; CPT PV = 318. 88 • Year 3 CF: N = 3; I/Y = 12; FV = 600; CPT PV = 427. 07 • Year 4 CF: N = 4; I/Y = 12; FV = 800; CPT PV = 508. 41 • Total PV = 178. 57 + 318. 88 + 427. 07 + 508. 41 = 1432. 93 © 2013 Mc. Graw-Hill Ryerson Limited 6 -9
LO 1 Multiple Cash Flows - PV Example 1 continued • Calculator Approach • Year 1 CF: N = 1; I/Y = 12; FV = 200; CPT PV = 178. 57 • Year 2 CF: N = 2; I/Y = 12; FV = 400; CPT PV = 318. 88 • Year 3 CF: N = 3; I/Y = 12; FV = 600; CPT PV = 427. 07 • Year 4 CF: N = 4; I/Y = 12; FV = 800; CPT PV = 508. 41 • Total PV = 178. 57 + 318. 88 + 427. 07 + 508. 41 = 1432. 93 © 2013 Mc. Graw-Hill Ryerson Limited 6 -9
 LO 1 Multiple Cash Flows Using a Spreadsheet • You can use the PV or FV functions in Excel to find the present value or future value of a set of cash flows • Setting the data up is half the battle – if it is set up properly, then you can just copy the formulas • Click on the Excel icon for an example © 2013 Mc. Graw-Hill Ryerson Limited 6 -10
LO 1 Multiple Cash Flows Using a Spreadsheet • You can use the PV or FV functions in Excel to find the present value or future value of a set of cash flows • Setting the data up is half the battle – if it is set up properly, then you can just copy the formulas • Click on the Excel icon for an example © 2013 Mc. Graw-Hill Ryerson Limited 6 -10
 LO 1 Multiple Cash Flows – PV Example 2 • You are considering an investment that will pay you $1000 in one year, $2000 in two years and $3000 in three years. If you want to earn 10% on your money, how much would you be willing to pay? © 2013 Mc. Graw-Hill Ryerson Limited 6 -11
LO 1 Multiple Cash Flows – PV Example 2 • You are considering an investment that will pay you $1000 in one year, $2000 in two years and $3000 in three years. If you want to earn 10% on your money, how much would you be willing to pay? © 2013 Mc. Graw-Hill Ryerson Limited 6 -11
 LO 1 Multiple Cash Flows – PV Example 2 continued • Formula Approach • • PV = 1000 / (1. 1)1 = 909. 09 PV = 2000 / (1. 1)2 = 1652. 89 PV = 3000 / (1. 1)3 = 2253. 94 PV = 909. 09 + 1652. 89 + 2253. 94 = 4815. 93 • Calculator Approach • • N = 1; I/Y = 10; FV = 1000; CPT PV = -909. 09 N = 2; I/Y = 10; FV = 2000; CPT PV = -1652. 89 N = 3; I/Y = 10; FV = 3000; CPT PV = -2253. 94 PV = 909. 09 + 1652. 89 + 2253. 94 = 4815. 93 © 2013 Mc. Graw-Hill Ryerson Limited 6 -12
LO 1 Multiple Cash Flows – PV Example 2 continued • Formula Approach • • PV = 1000 / (1. 1)1 = 909. 09 PV = 2000 / (1. 1)2 = 1652. 89 PV = 3000 / (1. 1)3 = 2253. 94 PV = 909. 09 + 1652. 89 + 2253. 94 = 4815. 93 • Calculator Approach • • N = 1; I/Y = 10; FV = 1000; CPT PV = -909. 09 N = 2; I/Y = 10; FV = 2000; CPT PV = -1652. 89 N = 3; I/Y = 10; FV = 3000; CPT PV = -2253. 94 PV = 909. 09 + 1652. 89 + 2253. 94 = 4815. 93 © 2013 Mc. Graw-Hill Ryerson Limited 6 -12
 LO 1 Multiple Uneven Cash Flows – Using the Calculator • Another way to use the financial calculator for uneven cash flows is to use the cash flow keys • Texas Instruments BA-II Plus • Press CF and enter the cash flows beginning with year 0 • You have to press the “Enter” key for each cash flow • Use the down arrow key to move to the next cash flow • The “F” is the number of times a given cash flow occurs in consecutive years • Use the NPV key to compute the present value by entering the interest rate for I, pressing the down arrow and then compute • Clear the cash flow keys by pressing CF and then CLR Work © 2013 Mc. Graw-Hill Ryerson Limited 6 -13
LO 1 Multiple Uneven Cash Flows – Using the Calculator • Another way to use the financial calculator for uneven cash flows is to use the cash flow keys • Texas Instruments BA-II Plus • Press CF and enter the cash flows beginning with year 0 • You have to press the “Enter” key for each cash flow • Use the down arrow key to move to the next cash flow • The “F” is the number of times a given cash flow occurs in consecutive years • Use the NPV key to compute the present value by entering the interest rate for I, pressing the down arrow and then compute • Clear the cash flow keys by pressing CF and then CLR Work © 2013 Mc. Graw-Hill Ryerson Limited 6 -13
 LO 1 Decisions, Decisions • Your broker calls you and tells you that he has this great investment opportunity. If you invest $100 today, you will receive $40 in one year and $75 in two years. If you require a 15% return on investments of this risk, should you take the investment? • Use the CF keys to compute the value of the investment • CF; CF 0 = 0; C 01 = 40; F 01 = 1; C 02 = 75; F 02 =1 • NPV; I = 15; CPT NPV = 91. 49 • No – the broker is charging more than you would be willing to pay. © 2013 Mc. Graw-Hill Ryerson Limited 6 -14
LO 1 Decisions, Decisions • Your broker calls you and tells you that he has this great investment opportunity. If you invest $100 today, you will receive $40 in one year and $75 in two years. If you require a 15% return on investments of this risk, should you take the investment? • Use the CF keys to compute the value of the investment • CF; CF 0 = 0; C 01 = 40; F 01 = 1; C 02 = 75; F 02 =1 • NPV; I = 15; CPT NPV = 91. 49 • No – the broker is charging more than you would be willing to pay. © 2013 Mc. Graw-Hill Ryerson Limited 6 -14
 LO 1 Saving For Retirement • You are offered the opportunity to put some money away for retirement. You will receive five annual payments of $25, 000 each beginning in 40 years. How much would you be willing to invest today if you desire an interest rate of 12%? © 2013 Mc. Graw-Hill Ryerson Limited 6 -15
LO 1 Saving For Retirement • You are offered the opportunity to put some money away for retirement. You will receive five annual payments of $25, 000 each beginning in 40 years. How much would you be willing to invest today if you desire an interest rate of 12%? © 2013 Mc. Graw-Hill Ryerson Limited 6 -15
 LO 1 Saving For Retirement Timeline 0 1 2 … 39 40 41 42 43 44 0 0 0 … 0 25 K 25 K 25 K Notice that the year 0 cash flow = 0 (CF 0 = 0) The cash flows years 1 – 39 are 0 (C 01 = 0; F 01 = 39) The cash flows years 40 – 44 are 25, 000 (C 02 = 25, 000; F 02 = 5) © 2013 Mc. Graw-Hill Ryerson Limited 6 -16
LO 1 Saving For Retirement Timeline 0 1 2 … 39 40 41 42 43 44 0 0 0 … 0 25 K 25 K 25 K Notice that the year 0 cash flow = 0 (CF 0 = 0) The cash flows years 1 – 39 are 0 (C 01 = 0; F 01 = 39) The cash flows years 40 – 44 are 25, 000 (C 02 = 25, 000; F 02 = 5) © 2013 Mc. Graw-Hill Ryerson Limited 6 -16
 LO 1 Saving For Retirement continued • Calculator Approach • Use cash flow keys: • CF; CF 0 = 0; C 01 = 0; F 01 = 39; C 02 = 25000; F 02 = 5; NPV; I = 12; CPT NPV = 1084. 71 © 2013 Mc. Graw-Hill Ryerson Limited 6 -17
LO 1 Saving For Retirement continued • Calculator Approach • Use cash flow keys: • CF; CF 0 = 0; C 01 = 0; F 01 = 39; C 02 = 25000; F 02 = 5; NPV; I = 12; CPT NPV = 1084. 71 © 2013 Mc. Graw-Hill Ryerson Limited 6 -17
 LO 1 Quick Quiz – Part I • Suppose you are looking at the following possible cash flows: Year 1 CF = $100; Years 2 and 3 CFs = $200; Years 4 and 5 CFs = $300. The required discount rate is 7% • What is the value of the cash flows at year 5? • What is the value of the cash flows today? • What is the value of the cash flows at year 3? 6 -18 © 2013 Mc. Graw-Hill Ryerson Limited
LO 1 Quick Quiz – Part I • Suppose you are looking at the following possible cash flows: Year 1 CF = $100; Years 2 and 3 CFs = $200; Years 4 and 5 CFs = $300. The required discount rate is 7% • What is the value of the cash flows at year 5? • What is the value of the cash flows today? • What is the value of the cash flows at year 3? 6 -18 © 2013 Mc. Graw-Hill Ryerson Limited
 LO 1 Annuities and Perpetuities 6. 2 • Annuity – finite series of equal payments that occur at regular intervals • If the first payment occurs at the end of the period, it is called an ordinary annuity • If the first payment occurs at the beginning of the period, it is called an annuity due • Perpetuity – infinite series of equal payments © 2013 Mc. Graw-Hill Ryerson Limited 6 -19
LO 1 Annuities and Perpetuities 6. 2 • Annuity – finite series of equal payments that occur at regular intervals • If the first payment occurs at the end of the period, it is called an ordinary annuity • If the first payment occurs at the beginning of the period, it is called an annuity due • Perpetuity – infinite series of equal payments © 2013 Mc. Graw-Hill Ryerson Limited 6 -19
 LO 1 Annuities and Perpetuities – Basic Formulas • Perpetuity: PV = C / r • Annuities: © 2013 Mc. Graw-Hill Ryerson Limited 6 -20
LO 1 Annuities and Perpetuities – Basic Formulas • Perpetuity: PV = C / r • Annuities: © 2013 Mc. Graw-Hill Ryerson Limited 6 -20
 LO 1 Annuities and the Calculator • You can use the PMT key on the calculator for the equal payment • The sign convention still holds • Ordinary annuity versus annuity due • You can switch your calculator between the two types by using the 2 nd BGN 2 nd Set on the TI BA-II Plus • If you see “BGN” or “Begin” in the display of your calculator, you have it set for an annuity due • Most problems are ordinary annuities © 2013 Mc. Graw-Hill Ryerson Limited 6 -21
LO 1 Annuities and the Calculator • You can use the PMT key on the calculator for the equal payment • The sign convention still holds • Ordinary annuity versus annuity due • You can switch your calculator between the two types by using the 2 nd BGN 2 nd Set on the TI BA-II Plus • If you see “BGN” or “Begin” in the display of your calculator, you have it set for an annuity due • Most problems are ordinary annuities © 2013 Mc. Graw-Hill Ryerson Limited 6 -21
 LO 1 Annuity – Example 1 • After carefully going over your budget, you have determined that you can afford to pay $632 per month towards a new sports car. Your bank will lend to you at 1% per month for 48 months. How much can you borrow? © 2013 Mc. Graw-Hill Ryerson Limited 6 -22
LO 1 Annuity – Example 1 • After carefully going over your budget, you have determined that you can afford to pay $632 per month towards a new sports car. Your bank will lend to you at 1% per month for 48 months. How much can you borrow? © 2013 Mc. Graw-Hill Ryerson Limited 6 -22
 LO 1 Annuity – Example 1 continued • You borrow money TODAY so you need to compute the present value. • Formula Approach • Calculator Approach • 48 N; 1 I/Y; -632 PMT; CPT PV = 23, 999. 54 ($24, 000) © 2013 Mc. Graw-Hill Ryerson Limited 6 -23
LO 1 Annuity – Example 1 continued • You borrow money TODAY so you need to compute the present value. • Formula Approach • Calculator Approach • 48 N; 1 I/Y; -632 PMT; CPT PV = 23, 999. 54 ($24, 000) © 2013 Mc. Graw-Hill Ryerson Limited 6 -23
 LO 1 Annuity – Sweepstakes Example • Suppose you win the Publishers Clearinghouse $10 million sweepstakes. The money is paid in equal annual installments of $333, 333. 33 over 30 years. If the appropriate discount rate is 5%, how much is the sweepstakes actually worth today? • Formula Approach • PV = 333, 333. 33[1 – 1/1. 0530] /. 05 = 5, 124, 150. 29 • Calculator Approach • 30 N; 5 I/Y; 333, 333. 33 PMT; CPT PV = -5, 124, 150. 29 © 2013 Mc. Graw-Hill Ryerson Limited 6 -24
LO 1 Annuity – Sweepstakes Example • Suppose you win the Publishers Clearinghouse $10 million sweepstakes. The money is paid in equal annual installments of $333, 333. 33 over 30 years. If the appropriate discount rate is 5%, how much is the sweepstakes actually worth today? • Formula Approach • PV = 333, 333. 33[1 – 1/1. 0530] /. 05 = 5, 124, 150. 29 • Calculator Approach • 30 N; 5 I/Y; 333, 333. 33 PMT; CPT PV = -5, 124, 150. 29 © 2013 Mc. Graw-Hill Ryerson Limited 6 -24
 LO 1 Annuities on the Spreadsheet Example • The present value and future value formulas in a spreadsheet include a place for annuity payments • Click on the Excel icon to see an example © 2013 Mc. Graw-Hill Ryerson Limited 6 -25
LO 1 Annuities on the Spreadsheet Example • The present value and future value formulas in a spreadsheet include a place for annuity payments • Click on the Excel icon to see an example © 2013 Mc. Graw-Hill Ryerson Limited 6 -25
 LO 1 Quick Quiz – Part II • You know the payment amount for a loan and you want to know how much was borrowed. Do you compute a present value or a future value? • You want to receive $5, 000 per month in retirement. If you can earn 0. 75% per month and you expect to need the income for 25 years, how much do you need to have in your account at retirement? © 2013 Mc. Graw-Hill Ryerson Limited 6 -26
LO 1 Quick Quiz – Part II • You know the payment amount for a loan and you want to know how much was borrowed. Do you compute a present value or a future value? • You want to receive $5, 000 per month in retirement. If you can earn 0. 75% per month and you expect to need the income for 25 years, how much do you need to have in your account at retirement? © 2013 Mc. Graw-Hill Ryerson Limited 6 -26
 LO 1 Future Values for Annuities – Example 1 • Suppose you begin saving for your retirement by depositing $2000 per year in an RRSP. If the interest rate is 7. 5%, how much will you have in 40 years? • Formula Approach • FV = 2000(1. 07540 – 1)/. 075 = 454, 513. 04 • Calculator Approach • • • Remember the sign convention!!! 40 N 7. 5 I/Y -2000 PMT CPT FV = 454, 513. 04 © 2013 Mc. Graw-Hill Ryerson Limited 6 -27
LO 1 Future Values for Annuities – Example 1 • Suppose you begin saving for your retirement by depositing $2000 per year in an RRSP. If the interest rate is 7. 5%, how much will you have in 40 years? • Formula Approach • FV = 2000(1. 07540 – 1)/. 075 = 454, 513. 04 • Calculator Approach • • • Remember the sign convention!!! 40 N 7. 5 I/Y -2000 PMT CPT FV = 454, 513. 04 © 2013 Mc. Graw-Hill Ryerson Limited 6 -27
 LO 1 Annuity Due – Example 1 • You are saving for a new house and you put $10, 000 per year in an account paying 8% compounded annually. The first payment is made today. How much will you have at the end of 3 years? © 2013 Mc. Graw-Hill Ryerson Limited 6 -28
LO 1 Annuity Due – Example 1 • You are saving for a new house and you put $10, 000 per year in an account paying 8% compounded annually. The first payment is made today. How much will you have at the end of 3 years? © 2013 Mc. Graw-Hill Ryerson Limited 6 -28
 LO 1 Annuity Due – Example 1 Timeline 0 10000 1 10000 2 3 10000 32, 464 35, 061. 12 © 2013 Mc. Graw-Hill Ryerson Limited 6 -29
LO 1 Annuity Due – Example 1 Timeline 0 10000 1 10000 2 3 10000 32, 464 35, 061. 12 © 2013 Mc. Graw-Hill Ryerson Limited 6 -29
 LO 1 Annuity Due – Example 1 continued • Formula Approach • FV = 10, 000[(1. 083 – 1) /. 08](1. 08) = 35, 061. 12 • Calculator Approach • 2 nd BGN 2 nd Set (you should see BGN in the display) • 3 N • -10, 000 PMT • 8 I/Y • CPT FV = 35, 061. 12 • 2 nd BGN 2 nd Set (be sure to change it back to an ordinary annuity) © 2013 Mc. Graw-Hill Ryerson Limited 6 -30
LO 1 Annuity Due – Example 1 continued • Formula Approach • FV = 10, 000[(1. 083 – 1) /. 08](1. 08) = 35, 061. 12 • Calculator Approach • 2 nd BGN 2 nd Set (you should see BGN in the display) • 3 N • -10, 000 PMT • 8 I/Y • CPT FV = 35, 061. 12 • 2 nd BGN 2 nd Set (be sure to change it back to an ordinary annuity) © 2013 Mc. Graw-Hill Ryerson Limited 6 -30
 LO 1 Perpetuity – Example 1 • The Home Bank of Canada want to sell preferred stock at $100 per share. A very similar issue of preferred stock already outstanding has a price of $40 per share and offers a dividend of $1 every quarter. What dividend would the Home Bank have to offer if its preferred stock is going to sell? © 2013 Mc. Graw-Hill Ryerson Limited 6 -31
LO 1 Perpetuity – Example 1 • The Home Bank of Canada want to sell preferred stock at $100 per share. A very similar issue of preferred stock already outstanding has a price of $40 per share and offers a dividend of $1 every quarter. What dividend would the Home Bank have to offer if its preferred stock is going to sell? © 2013 Mc. Graw-Hill Ryerson Limited 6 -31
 LO 1 Perpetuity – Example 1 continued • Perpetuity formula: PV = C / r • First, find the required return for the comparable issue: • 40 = 1 / r • r =. 025 or 2. 5% per quarter • Then, using the required return found above, find the dividend for new preferred issue: • 100 = C /. 025 • C = 2. 50 per quarter © 2013 Mc. Graw-Hill Ryerson Limited 6 -32
LO 1 Perpetuity – Example 1 continued • Perpetuity formula: PV = C / r • First, find the required return for the comparable issue: • 40 = 1 / r • r =. 025 or 2. 5% per quarter • Then, using the required return found above, find the dividend for new preferred issue: • 100 = C /. 025 • C = 2. 50 per quarter © 2013 Mc. Graw-Hill Ryerson Limited 6 -32
 LO 1 Growing Perpetuity • The perpetuities discussed so far have constant payments • Growing perpetuities have cash flows that grow at a constant rate and continue forever • Growing perpetuity formula: © 2013 Mc. Graw-Hill Ryerson Limited 6 -33
LO 1 Growing Perpetuity • The perpetuities discussed so far have constant payments • Growing perpetuities have cash flows that grow at a constant rate and continue forever • Growing perpetuity formula: © 2013 Mc. Graw-Hill Ryerson Limited 6 -33
 LO 1 Growing Perpetuity – Example 1 • Hoffstein Corporation is expected to pay a dividend of $3 per share next year. Investors anticipate that the annual dividend will rise by 6% per year forever. The required rate of return is 11%. What is the price of the stock today? © 2013 Mc. Graw-Hill Ryerson Limited 6 -34
LO 1 Growing Perpetuity – Example 1 • Hoffstein Corporation is expected to pay a dividend of $3 per share next year. Investors anticipate that the annual dividend will rise by 6% per year forever. The required rate of return is 11%. What is the price of the stock today? © 2013 Mc. Graw-Hill Ryerson Limited 6 -34
 LO 1 Growing Annuity • Growing annuities have a finite number of growing cash flows • Growing annuity formula: © 2013 Mc. Graw-Hill Ryerson Limited 6 -35
LO 1 Growing Annuity • Growing annuities have a finite number of growing cash flows • Growing annuity formula: © 2013 Mc. Graw-Hill Ryerson Limited 6 -35
 LO 1 Growing Annuity – Example 1 • Gilles Lebouder has just been offered a job at $50, 000 a year. He anticipates his salary will increase by 5% a year until his retirement in 40 years. Given an interest rate of 8%, what is the present value of his lifetime salary? © 2013 Mc. Graw-Hill Ryerson Limited 6 -36
LO 1 Growing Annuity – Example 1 • Gilles Lebouder has just been offered a job at $50, 000 a year. He anticipates his salary will increase by 5% a year until his retirement in 40 years. Given an interest rate of 8%, what is the present value of his lifetime salary? © 2013 Mc. Graw-Hill Ryerson Limited 6 -36
 LO 1 Quick Quiz – Part IV • You want to have $1 million to use for retirement in 35 years. If you can earn 1% per month, how much do you need to deposit on a monthly basis if the first payment is made in one month? • What if the first payment is made today? • You are considering preferred stock that pays a quarterly dividend of $1. 50. If your desired return is 3% per quarter, how much would you be willing to pay? © 2013 Mc. Graw-Hill Ryerson Limited 6 -37
LO 1 Quick Quiz – Part IV • You want to have $1 million to use for retirement in 35 years. If you can earn 1% per month, how much do you need to deposit on a monthly basis if the first payment is made in one month? • What if the first payment is made today? • You are considering preferred stock that pays a quarterly dividend of $1. 50. If your desired return is 3% per quarter, how much would you be willing to pay? © 2013 Mc. Graw-Hill Ryerson Limited 6 -37
 LO 1 Work the Web Example • Another online financial calculator can be found at Money. Chimp • Click on the web surfer and work the following example • Choose calculator and then annuity • You just inherited $5 million. If you can earn 6% on your money, how much can you withdraw each year for the next 40 years? • Payment = $332, 307. 68 © 2013 Mc. Graw-Hill Ryerson Limited 6 -38
LO 1 Work the Web Example • Another online financial calculator can be found at Money. Chimp • Click on the web surfer and work the following example • Choose calculator and then annuity • You just inherited $5 million. If you can earn 6% on your money, how much can you withdraw each year for the next 40 years? • Payment = $332, 307. 68 © 2013 Mc. Graw-Hill Ryerson Limited 6 -38
 LO 1 Table 6. 2 – Summary of Annuity and Perpetuity Calculations © 2013 Mc. Graw-Hill Ryerson Limited 6 -39
LO 1 Table 6. 2 – Summary of Annuity and Perpetuity Calculations © 2013 Mc. Graw-Hill Ryerson Limited 6 -39


