 ЛК. 13 – ІНФОРМОВАНИЙ ПОШУК ТА ПОШУК В УМОВАХ ПРОТИДІЇ
ЛК. 13 – ІНФОРМОВАНИЙ ПОШУК ТА ПОШУК В УМОВАХ ПРОТИДІЇ
 Перелік питань 1. Основи інформованого пошуку: 2. 3. 4. 5. евристична функція, жадібний пошук за першою найкращою відповідністю. Метод мінімізації сумарної оцінки вартості рішення та алгоритми локального пошуку. Генетичний алгоритм. Пошук в умовах протидії. Алгоритм минимакса або мінімаксний алгоритм. Шахові програми
Перелік питань 1. Основи інформованого пошуку: 2. 3. 4. 5. евристична функція, жадібний пошук за першою найкращою відповідністю. Метод мінімізації сумарної оцінки вартості рішення та алгоритми локального пошуку. Генетичний алгоритм. Пошук в умовах протидії. Алгоритм минимакса або мінімаксний алгоритм. Шахові програми
 1. 1 Основи інформованого пошуку: евристична функція, жадібний пошук за першою найкращою відповідністю Представляється доцільним поліпшити сліпий пошук в тих випадках, коли є яка -небудь додаткова інформація. Ми не розглядаємо випадок, коли точно відомий шлях до мети. В останньому випадку задача вже вирішена. Йдеться про інформацію, яка спостерігається, але не дає прямої відповіді, як рухатися до мети. Розглянемо наступну задачу. Нехай нам потрібно добратися з Талліна до Москви повітряним транспортом. Відстані між містами і повітряні траси показані на рисунку
1. 1 Основи інформованого пошуку: евристична функція, жадібний пошук за першою найкращою відповідністю Представляється доцільним поліпшити сліпий пошук в тих випадках, коли є яка -небудь додаткова інформація. Ми не розглядаємо випадок, коли точно відомий шлях до мети. В останньому випадку задача вже вирішена. Йдеться про інформацію, яка спостерігається, але не дає прямої відповіді, як рухатися до мети. Розглянемо наступну задачу. Нехай нам потрібно добратися з Талліна до Москви повітряним транспортом. Відстані між містами і повітряні траси показані на рисунку
 Якби ми не мали ніяких даних про відстані, то мав би місце сліпий (непоінформований) пошук. Якщо ми знаємо тільки відстань від поточної точки до сусідніх, то ми в змозі виконати пошук за критерієм вартості. Найближчий пункт від Талліна - Гельсінкі (100 км), потім - Петербург (295), Рига (476), Твер (716), Москва (161). Загальна протяжність шляху - 1748 км, і вона суттєво відрізняється від оптимальної 957 км.
Якби ми не мали ніяких даних про відстані, то мав би місце сліпий (непоінформований) пошук. Якщо ми знаємо тільки відстань від поточної точки до сусідніх, то ми в змозі виконати пошук за критерієм вартості. Найближчий пункт від Талліна - Гельсінкі (100 км), потім - Петербург (295), Рига (476), Твер (716), Москва (161). Загальна протяжність шляху - 1748 км, і вона суттєво відрізняється від оптимальної 957 км.
 Доступними пунктами з Талліна є Хельсінкі (897 км), С. Петербург (634) і Рига (839). Прагнучи на кожному кроці максимально наблизитися до мети, ми виберемо на першому кроці С. Петербург, на другому кроці - Твер, потім Москву. Загальна протяжність шляху дорівнює оптимальної. Даний вид пошуку називається жадібним пошуком по першому найкращому відповідності.
Доступними пунктами з Талліна є Хельсінкі (897 км), С. Петербург (634) і Рига (839). Прагнучи на кожному кроці максимально наблизитися до мети, ми виберемо на першому кроці С. Петербург, на другому кроці - Твер, потім Москву. Загальна протяжність шляху дорівнює оптимальної. Даний вид пошуку називається жадібним пошуком по першому найкращому відповідності.
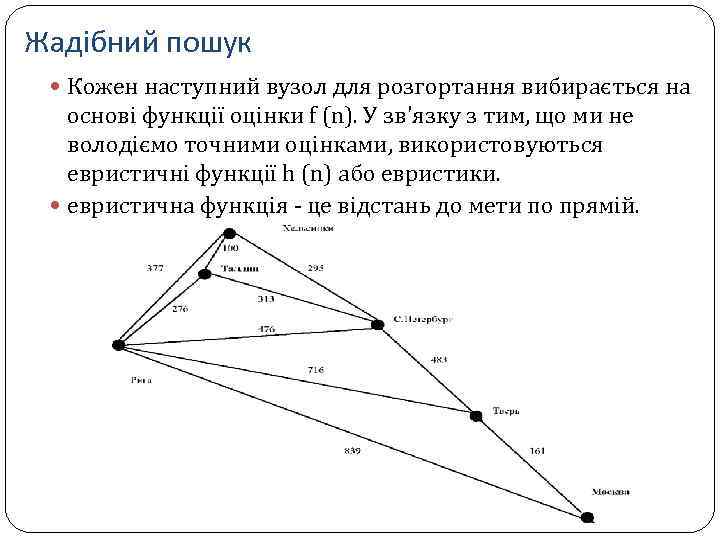 Жадібний пошук Кожен наступний вузол для розгортання вибирається на основі функції оцінки f (n). У зв'язку з тим, що ми не володіємо точними оцінками, використовуються евристичні функції h (n) або евристики. евристична функція - це відстань до мети по прямій.
Жадібний пошук Кожен наступний вузол для розгортання вибирається на основі функції оцінки f (n). У зв'язку з тим, що ми не володіємо точними оцінками, використовуються евристичні функції h (n) або евристики. евристична функція - це відстань до мети по прямій.
 Ця евристика не є свідомо оптимальної. Якщо, наприклад, між Твер'ю і Москвою літаки не літають, то оптимальний маршрут Таллін - Рига Москва буде істотно відрізнятися від запропонованого алгоритмом жодного пошуку по першому найкращому збігу: Таллін - С. Петербург Твер - Рига - Москва.
Ця евристика не є свідомо оптимальної. Якщо, наприклад, між Твер'ю і Москвою літаки не літають, то оптимальний маршрут Таллін - Рига Москва буде істотно відрізнятися від запропонованого алгоритмом жодного пошуку по першому найкращому збігу: Таллін - С. Петербург Твер - Рига - Москва.
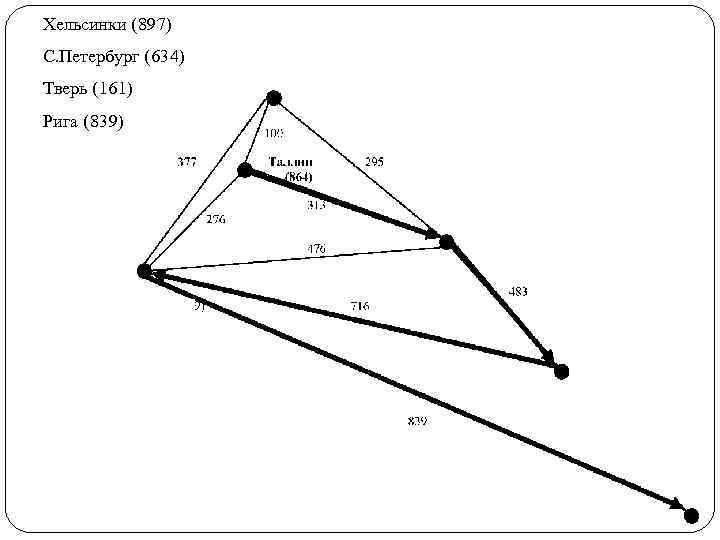 Хельсинки (897) С. Петербург (634) Тверь (161) Рига (839)
Хельсинки (897) С. Петербург (634) Тверь (161) Рига (839)
 СПР другого типу припускають доволі глибоке опрацювання даних, спеціально перетворених так, щоб їх було зручно використовувати під час прийняття рішень. Невід'ємним компонентом СПР цього рівня є правила прийняття рішень, які на основі агрегованих даних підказують менеджерському складу висновки і надають системі ознаки штучного інтелекту. Такі системи створюються тільки у тому разі, якщо структура бізнесу вже достатньо визначена і є підстави для узагальнення і аналізу не тільки даних, але й процесів їхнього опрацювання. Якщо АІС є не що інше, як розвиток системи оперативного управління виробничими процесами, то СППР у сучасному розумінні – це механізм розвитку бізнесу, який включає в себе деяку частину керуючої інформаційної системи, велику систему зовнішніх зв'язків підприємства, а також технологічні і маркетингові процеси розвитку виробництва.
СПР другого типу припускають доволі глибоке опрацювання даних, спеціально перетворених так, щоб їх було зручно використовувати під час прийняття рішень. Невід'ємним компонентом СПР цього рівня є правила прийняття рішень, які на основі агрегованих даних підказують менеджерському складу висновки і надають системі ознаки штучного інтелекту. Такі системи створюються тільки у тому разі, якщо структура бізнесу вже достатньо визначена і є підстави для узагальнення і аналізу не тільки даних, але й процесів їхнього опрацювання. Якщо АІС є не що інше, як розвиток системи оперативного управління виробничими процесами, то СППР у сучасному розумінні – це механізм розвитку бізнесу, який включає в себе деяку частину керуючої інформаційної системи, велику систему зовнішніх зв'язків підприємства, а також технологічні і маркетингові процеси розвитку виробництва.
 Особливий клас систем стратегічного управління і підтримки прийняття рішень – системи, що дають змогу здійснювати динамічне моделювання процесів. Під час використання методів динамічного моделювання діяльність компанії описується у вигляді математичної моделі, в якій усі бізнес-задачі і процеси подаються як система взаємопов'язаних обчислюваних показників. Сучасні діалогові системи прийняття та підтримки рішень тією чи іншою мірою реалізують етапи процесу прийняття рішень, причому їхню архітектуру доцільно розглядати, виділяючи такі рівні: мети, постановок задач, процедур, формальних моделей, алгоритмічних, програмних ресурсів. У межах інформаційного підходу СППР зараховують до класу автоматизованих інформаційних систем, основне призначення яких – поліпшити діяльність людини шляхом застосування інформаційних технологій (ІТ).
Особливий клас систем стратегічного управління і підтримки прийняття рішень – системи, що дають змогу здійснювати динамічне моделювання процесів. Під час використання методів динамічного моделювання діяльність компанії описується у вигляді математичної моделі, в якій усі бізнес-задачі і процеси подаються як система взаємопов'язаних обчислюваних показників. Сучасні діалогові системи прийняття та підтримки рішень тією чи іншою мірою реалізують етапи процесу прийняття рішень, причому їхню архітектуру доцільно розглядати, виділяючи такі рівні: мети, постановок задач, процедур, формальних моделей, алгоритмічних, програмних ресурсів. У межах інформаційного підходу СППР зараховують до класу автоматизованих інформаційних систем, основне призначення яких – поліпшити діяльність людини шляхом застосування інформаційних технологій (ІТ).
 2. Узагальнена архітектура СПР, складається з п’яти різних частин, а саме: системи управління даними (the data management system – DBMS); системи управління моделями (the model management system – MBMS); машини знань (the knowledge engine (KE)); інтерфейсу користувача (the user interface); користувачів (the user(s))
2. Узагальнена архітектура СПР, складається з п’яти різних частин, а саме: системи управління даними (the data management system – DBMS); системи управління моделями (the model management system – MBMS); машини знань (the knowledge engine (KE)); інтерфейсу користувача (the user interface); користувачів (the user(s))
 Жадібний пошук по першому найкращому збігу є пошук в глибину і страждає від тих же недоліків. На останній схемі без запобігання повторюваних станів можливо нескінченне блукання по відрізку С. Петербург - Твер - С. Петербург і т. д. В найгіршому варіанті складність методу становить b^m, де b - коефіцієнт розгалуження, m максимальна глибина простору пошуку. Хороша евристична функція дозволяє істотно знизити таку складність.
Жадібний пошук по першому найкращому збігу є пошук в глибину і страждає від тих же недоліків. На останній схемі без запобігання повторюваних станів можливо нескінченне блукання по відрізку С. Петербург - Твер - С. Петербург і т. д. В найгіршому варіанті складність методу становить b^m, де b - коефіцієнт розгалуження, m максимальна глибина простору пошуку. Хороша евристична функція дозволяє істотно знизити таку складність.
 2 Метод мінімізації сумарної оцінки вартості рішення та алгоритми локального пошуку Оптимальний маршрут має мінімальну протяжність, і це факт бажано використовувати на кожному кроці пошуку, а не в самому кінці для оцінки результату Функція оцінки f (n) на кожному кроці обчислюється як: f(n) = g(n) + h(n) де g (n) - вартість досягнення n-го вузла, h (n) евристична функція вартості досягнення мети з nго вузла.
2 Метод мінімізації сумарної оцінки вартості рішення та алгоритми локального пошуку Оптимальний маршрут має мінімальну протяжність, і це факт бажано використовувати на кожному кроці пошуку, а не в самому кінці для оцінки результату Функція оцінки f (n) на кожному кроці обчислюється як: f(n) = g(n) + h(n) де g (n) - вартість досягнення n-го вузла, h (n) евристична функція вартості досягнення мети з nго вузла.
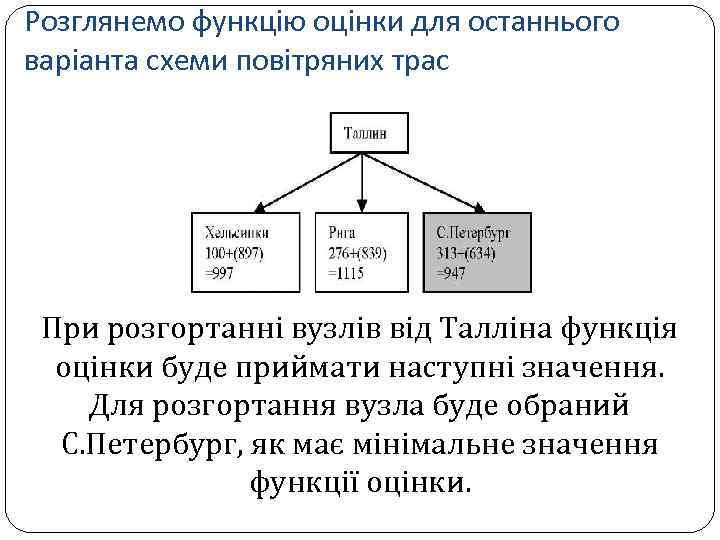 Розглянемо функцію оцінки для останнього варіанта схеми повітряних трас При розгортанні вузлів від Талліна функція оцінки буде приймати наступні значення. Для розгортання вузла буде обраний С. Петербург, як має мінімальне значення функції оцінки.
Розглянемо функцію оцінки для останнього варіанта схеми повітряних трас При розгортанні вузлів від Талліна функція оцінки буде приймати наступні значення. Для розгортання вузла буде обраний С. Петербург, як має мінімальне значення функції оцінки.
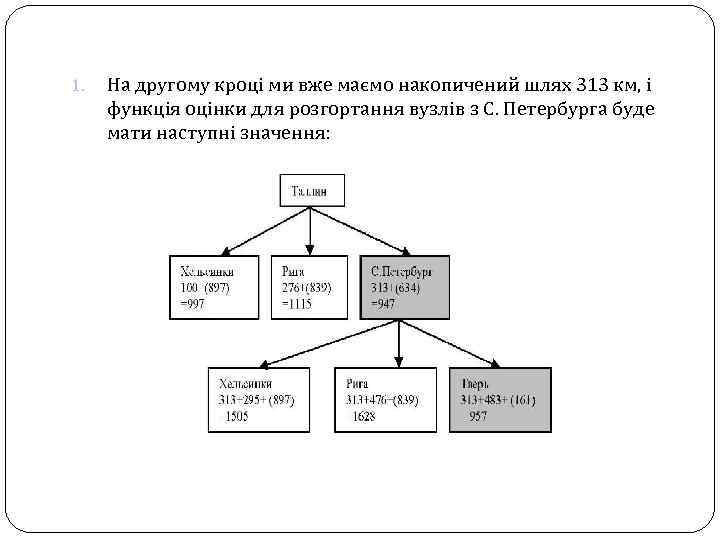 1. На другому кроці ми вже маємо накопичений шлях 313 км, і функція оцінки для розгортання вузлів з С. Петербурга буде мати наступні значення:
1. На другому кроці ми вже маємо накопичений шлях 313 км, і функція оцінки для розгортання вузлів з С. Петербурга буде мати наступні значення:
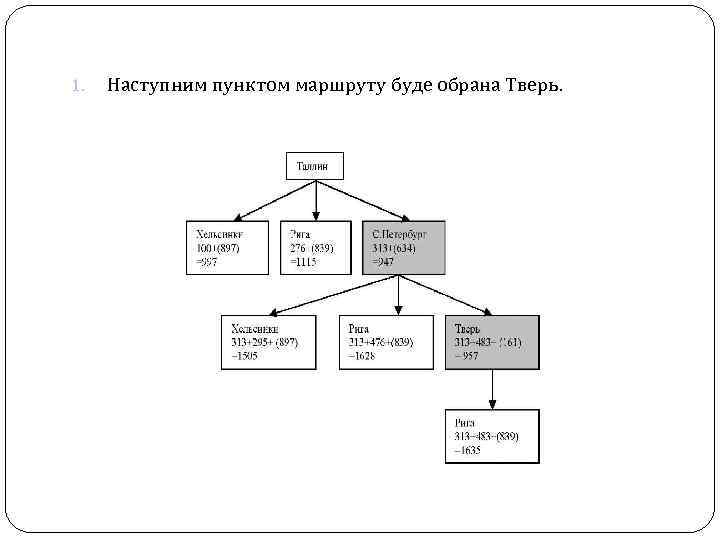 1. Наступним пунктом маршруту буде обрана Тверь.
1. Наступним пунктом маршруту буде обрана Тверь.
 З Твері є шлях тільки до Риги, але функція оцінки набагато вище, ніж при русі по маршруту Таллінн Рига. Отже, ця гілка (Таллін - С. Петербург - Твер Рига -. . . ) свідомо не дає оптимального рішення, і для розгортання потрібно замість С. -Петербурга обрати інше місто. Наступним після С. Петербурга за зростанням функції оцінки є Хельсінкі. При його розгортанні отримуємо такі значення функції оцінки:
З Твері є шлях тільки до Риги, але функція оцінки набагато вище, ніж при русі по маршруту Таллінн Рига. Отже, ця гілка (Таллін - С. Петербург - Твер Рига -. . . ) свідомо не дає оптимального рішення, і для розгортання потрібно замість С. -Петербурга обрати інше місто. Наступним після С. Петербурга за зростанням функції оцінки є Хельсінкі. При його розгортанні отримуємо такі значення функції оцінки:
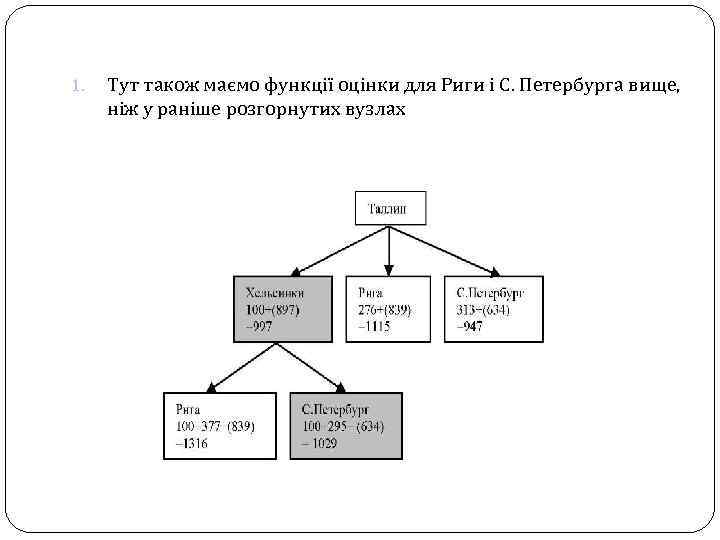 1. Тут також маємо функції оцінки для Риги і С. Петербурга вище, ніж у раніше розгорнутих вузлах
1. Тут також маємо функції оцінки для Риги і С. Петербурга вище, ніж у раніше розгорнутих вузлах
 Отже, необхідно розгорнути вузол Рига: Наступним пунктом маршруту буде обрана Твер. З Риги ми прямо потрапляємо в Москву. Рішення знайдено і воно є оптимальним. Зауважимо, що функція оцінки є оптимістичною, оскільки її частина - це відстань по прямій, а реальний шлях ніяк не може бути коротшим. Хельсинки С. Петербург Москва 276+716+(161) 276+377+(897) 276+476+ (634) = 276+(839) =1153 =1550 1386 =1115 Тверь
Отже, необхідно розгорнути вузол Рига: Наступним пунктом маршруту буде обрана Твер. З Риги ми прямо потрапляємо в Москву. Рішення знайдено і воно є оптимальним. Зауважимо, що функція оцінки є оптимістичною, оскільки її частина - це відстань по прямій, а реальний шлях ніяк не може бути коротшим. Хельсинки С. Петербург Москва 276+716+(161) 276+377+(897) 276+476+ (634) = 276+(839) =1153 =1550 1386 =1115 Тверь
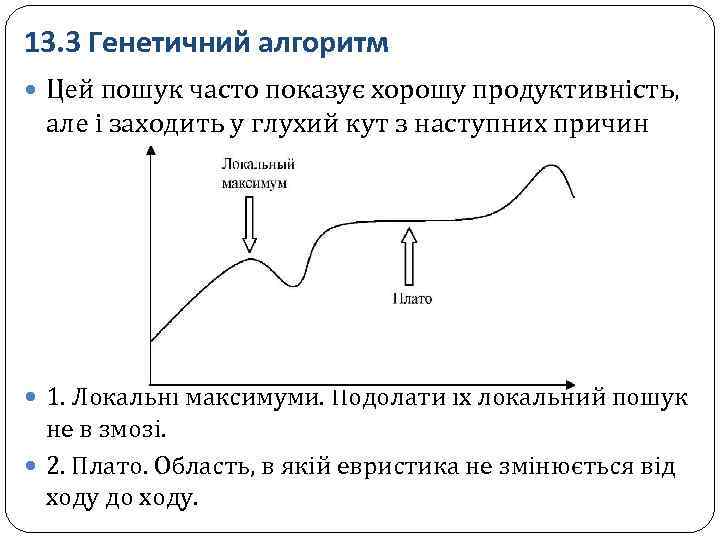 13. 3 Генетичний алгоритм Цей пошук часто показує хорошу продуктивність, але і заходить у глухий кут з наступних причин 1. Локальні максимуми. Подолати їх локальний пошук не в змозі. 2. Плато. Область, в якій евристика не змінюється від ходу до ходу.
13. 3 Генетичний алгоритм Цей пошук часто показує хорошу продуктивність, але і заходить у глухий кут з наступних причин 1. Локальні максимуми. Подолати їх локальний пошук не в змозі. 2. Плато. Область, в якій евристика не змінюється від ходу до ходу.
 Для усунення недоліків використовуються: рух у бік (дозвіл на певне число ходів при незмінній або погіршується евристиці); стохастичний пошук з сходженням до вершини (вибір випадковим чином одного з варіантів сходження до вершини); пошук з сходженням до вершини і перезапуском
Для усунення недоліків використовуються: рух у бік (дозвіл на певне число ходів при незмінній або погіршується евристиці); стохастичний пошук з сходженням до вершини (вибір випадковим чином одного з варіантів сходження до вершини); пошук з сходженням до вершини і перезапуском
 Основні етапи алгоритму Відбір Схрещування Мутації
Основні етапи алгоритму Відбір Схрещування Мутації
 Використання алгоритму 1. Вибираються позиції з кращими значеннями евристик (відбір). 2. Дошка «розрізається» по вертикалі або по горизонталі, і частини дошки від різних позицій з'єднуються разом (схрещування). 3. В отримані нові комбінації вносяться випадкові зміни (мутації). 4. Якщо отримана позиція гірше попередніх, вона відкидається, якщо краще, запам'ятовується (відбір). 5. З наявних кращих позицій все повторюється з п. 2. Генетичні алгоритми широко використовуються при вирішенні оптимізаційних задач
Використання алгоритму 1. Вибираються позиції з кращими значеннями евристик (відбір). 2. Дошка «розрізається» по вертикалі або по горизонталі, і частини дошки від різних позицій з'єднуються разом (схрещування). 3. В отримані нові комбінації вносяться випадкові зміни (мутації). 4. Якщо отримана позиція гірше попередніх, вона відкидається, якщо краще, запам'ятовується (відбір). 5. З наявних кращих позицій все повторюється з п. 2. Генетичні алгоритми широко використовуються при вирішенні оптимізаційних задач
 13. 4 Пошук в умовах протидії Існує клас задач, в яких присутній елемент невизначеності. До них відносяться всі ігрові завдання. Ми не будемо розглядати шахи (оцініть самі комбінаторну складність на перші 40 ходів, коефіцієнт розгалуження на першому ході 20), а повернемося до гри в сірники. Гравець і його супротивник мають 3 варіанти ходу на кожному етапі. Проблема полягає в тому, що якщо ми вибрали гілку дерева, яка приводить нас до перемоги, то це ніяк не влаштовує супротивника, і він зовсім не буде рухатися по цій гілці, а вживе всіх заходів, щоб не дати нам виграти.
13. 4 Пошук в умовах протидії Існує клас задач, в яких присутній елемент невизначеності. До них відносяться всі ігрові завдання. Ми не будемо розглядати шахи (оцініть самі комбінаторну складність на перші 40 ходів, коефіцієнт розгалуження на першому ході 20), а повернемося до гри в сірники. Гравець і його супротивник мають 3 варіанти ходу на кожному етапі. Проблема полягає в тому, що якщо ми вибрали гілку дерева, яка приводить нас до перемоги, то це ніяк не влаштовує супротивника, і він зовсім не буде рухатися по цій гілці, а вживе всіх заходів, щоб не дати нам виграти.
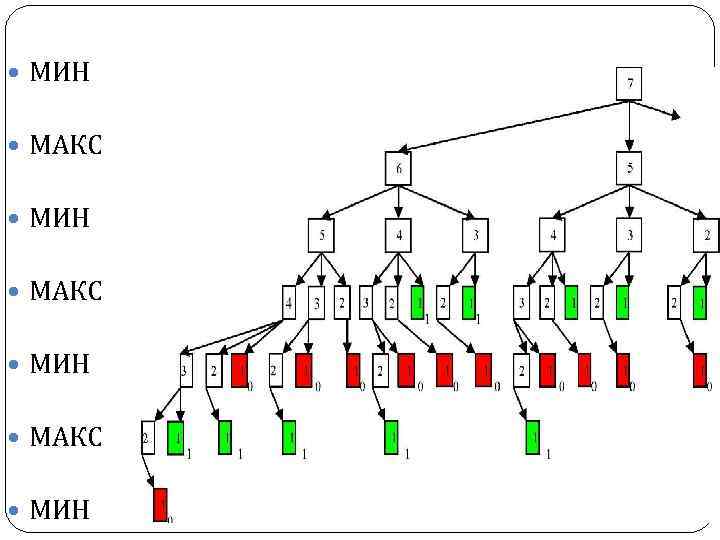
 Наша стратегія полягає в тому, щоб максимізувати результат, а стратегія супротивника - його мінімізувати. Назвемо для ясності супротивника - МІН, а себе МАКС. Спускаючись по дереву рішень, ми можемо дати оцінку кожному вузлу на самому нижньому рівні (показаний фрагмент дерева).
Наша стратегія полягає в тому, щоб максимізувати результат, а стратегія супротивника - його мінімізувати. Назвемо для ясності супротивника - МІН, а себе МАКС. Спускаючись по дереву рішень, ми можемо дати оцінку кожному вузлу на самому нижньому рівні (показаний фрагмент дерева).
 МИН МАКС МИН
МИН МАКС МИН
 Виграш Макс (1) показаний світлої заливкою, виграш МІНА (0) - темною. Припускаючи, що обидва гравці діють у своїх інтересах розумно, ми можемо дати оцінку кожному ходу гравців на кожен рівень вище, а саме: з усіх варіантів ходів МІН віддасть перевагу ті, які дадуть оцінку 0, а МАКС - ходи, що дають оцінку 1. Таким чином, оцінка кожного ходу Максим буде дорівнює мінімуму оцінок ходів у відповідь МІНА і навпаки, оцінка кожного ходу МІНА буде дорівнює максимуму оцінок ходів у відповідь Максим.
Виграш Макс (1) показаний світлої заливкою, виграш МІНА (0) - темною. Припускаючи, що обидва гравці діють у своїх інтересах розумно, ми можемо дати оцінку кожному ходу гравців на кожен рівень вище, а саме: з усіх варіантів ходів МІН віддасть перевагу ті, які дадуть оцінку 0, а МАКС - ходи, що дають оцінку 1. Таким чином, оцінка кожного ходу Максим буде дорівнює мінімуму оцінок ходів у відповідь МІНА і навпаки, оцінка кожного ходу МІНА буде дорівнює максимуму оцінок ходів у відповідь Максим.
 Даний алгоритм отримав назву алгоритм минимакса або мінімаксний алгоритм. Легко бачити, що оцінки по Мінімакс є песимістичними для кожного з гравців і, отже, гарантують успішний результат. У загальному випадку мінімаксний алгоритм складається з наступних кроків: 1. Вибір шкали оцінок результатів гри. 2. Спуск по дереву і привласнення оцінок кінцевим станам. 3. Послідовне привласнення оцінок батьківським вузлам: для МІНА - максимальної з дочірніх, для Максим - мінімальної. 4. Після присвоєння значення початкової позиції можна починати робити ходи.
Даний алгоритм отримав назву алгоритм минимакса або мінімаксний алгоритм. Легко бачити, що оцінки по Мінімакс є песимістичними для кожного з гравців і, отже, гарантують успішний результат. У загальному випадку мінімаксний алгоритм складається з наступних кроків: 1. Вибір шкали оцінок результатів гри. 2. Спуск по дереву і привласнення оцінок кінцевим станам. 3. Послідовне привласнення оцінок батьківським вузлам: для МІНА - максимальної з дочірніх, для Максим - мінімальної. 4. Після присвоєння значення початкової позиції можна починати робити ходи.
 13. 5 Шахові програми Більш практичним є застосування евристичних оцінок кожної позиції без спуску до нижніх листів дерева. Такий підхід використовується, наприклад, в шахових програмах, де шахістами давно відпрацьована методика оцінки як окремих фігур, так і позицій в цілому. Так, пішак має вартість 1, кінь чи слон - 3, тура - 5, ферзь - 9. Оцінюються також такі характеристики, як безпека короля, хороша пешечная структура і т. д. Таким чином, кожен хід може бути відразу оцінений. Це не означає, що можна обмежитися глибиною пошуку в один хід. Хороша позиція може бути досягнута через 5 або 8 ходів.
13. 5 Шахові програми Більш практичним є застосування евристичних оцінок кожної позиції без спуску до нижніх листів дерева. Такий підхід використовується, наприклад, в шахових програмах, де шахістами давно відпрацьована методика оцінки як окремих фігур, так і позицій в цілому. Так, пішак має вартість 1, кінь чи слон - 3, тура - 5, ферзь - 9. Оцінюються також такі характеристики, як безпека короля, хороша пешечная структура і т. д. Таким чином, кожен хід може бути відразу оцінений. Це не означає, що можна обмежитися глибиною пошуку в один хід. Хороша позиція може бути досягнута через 5 або 8 ходів.
 Модифікація альфа-бета відсікання в цьому випадку полягає в тому, щоб обмежити верхнє значення оцінки альфа (за принципом «від добра не шукають» ) і нижнє значення бета (мінімально допустиме тимчасове погіршення позиції). Тут все ж завжди є ризик пропустити відмінний хід або навпаки, «позіхнути» . Більш надійний підхід полягає у використанні раніше розглянутого ітеративного поглиблення в межах відведеного часу. Одне з рішень, зване пошуком спокійних позицій, полягає в тому, що зупиняти пошук можна тільки в спокійних позиціях, коли від ходу до ходу оцінка позиції змінюється незначно. У позиціях ж, істотно мінливих (наприклад, прохід пішака у ферзі), пошук треба продовжувати.
Модифікація альфа-бета відсікання в цьому випадку полягає в тому, щоб обмежити верхнє значення оцінки альфа (за принципом «від добра не шукають» ) і нижнє значення бета (мінімально допустиме тимчасове погіршення позиції). Тут все ж завжди є ризик пропустити відмінний хід або навпаки, «позіхнути» . Більш надійний підхід полягає у використанні раніше розглянутого ітеративного поглиблення в межах відведеного часу. Одне з рішень, зване пошуком спокійних позицій, полягає в тому, що зупиняти пошук можна тільки в спокійних позиціях, коли від ходу до ходу оцінка позиції змінюється незначно. У позиціях ж, істотно мінливих (наприклад, прохід пішака у ферзі), пошук треба продовжувати.
 При пошуку спокійних позицій виникає проблема усунення ефекту горизонту, який проявляється тоді, коли в перспективі мається хід, заподіює нам серйозний збиток, який ми можемо тільки відстрочити своїми ходами, але є неминучим. Наші ходи, відволікаючі противника (наприклад, оголошення серії шахів), можуть вивести небезпечний для нас хід за межі горизонту пошуку.
При пошуку спокійних позицій виникає проблема усунення ефекту горизонту, який проявляється тоді, коли в перспективі мається хід, заподіює нам серйозний збиток, який ми можемо тільки відстрочити своїми ходами, але є неминучим. Наші ходи, відволікаючі противника (наприклад, оголошення серії шахів), можуть вивести небезпечний для нас хід за межі горизонту пошуку.


