ЛК. 05 – Логічні задачі та пошук на основі логіки
Перелік питань 1. Постановка логічної задачі. 2. Метод міркувань вирішення логічних 3. 4. 5. 6. 7. задач. Метод таблиць вирішення логічних задач. Метод блок-схем вирішення логічних задач. Алгебраїчний метод вирішення логічних задач. Можливий і графічний спосіб вирішення системи. Пошук на основі логіки. Булева логіка.
14. 1 Постановка логічної задачі Рішенню будь-якої проблеми неодмінно передує точно визначена постановка задачі і її формулювання Рішення логічних завдань - цікаве і корисне заняття. Особливість в тому, що спочатку є тільки хибне та істинне твердження, і ніяких формул. Розглянемо кілька основних методів рішення, що мають свою сферу ефективності.
14. 2 Метод міркувань самий нехитрий - заснований на послідовних міркуваннях (випливають з умови задачі), і їх перевірці на істинність або хибність, причому всі наступні твердження грунтуються на вивіреному вихідному. Наприклад: Вік мами і доньки в сумі складає 98 років. Дочка народилася, коли мамі було 22 роки. Скільки років обом? Рішення: оскільки різниця в їхньому віці 22 року (саме в цьому віці у мами народилася дочка), то 98 - 22 = 76 (років). Це подвоєний вік дочки, тоді 76: 2 = 38 (років). Значить, матері 98 - 38 = 60 (років).
14. 3 Метод таблиць наочний метод, що припускає побудову таблиці за даними умови текстових завдань і послідовне її заповнення цифрами 0 або 1, в Залежно від отриманих висновків (брехня-істина). Наприклад. Є 8 літровий посудина, повний води. Як відлити 4 літри, якщо є порожні ємності об'ємом 3 та 5 літрів? Рішення: (…)
14. 4 Метод блок-схем застосуємо для рішення задач про ємностях і вазі, і набагато зручніше методу перебору варіантів (який не дозволяє вивести загальних правил). Спочатку формуються команди (тотожні виробленим операціями), а потім вибудовується їх схематична послідовність. Це і є відома в програмуванні блок-схема, яка веде до вирішення завдання. Логічним продовженням цього методу є метод вирішення за допомогою ЕОМ. Суть якого, в перекладанні отриманого алгоритму на мову програмування.
14. 5 Алгебраїчний метод вирішення передбачає вирішення систем логічних рівнянь. Всім твердженнями, що випливають з умови задачі, присвоюються літерні позначення і записуються у вигляді формул. Вирішуючи систему отриманих рівнянь (множачи одне на інше), виводиться істинне твердження.
14. 6 Графічний спосіб вирішення системи Для цього викреслюється схема логічних взаємозв'язків ("дерево логічних умов") на основі отриманих рівнянь системи. Причому логічна сума передбачає розгалуження, а твір - проходження умов один за одним. Рішення приходить на основі аналізу. Сюди ж відноситься і метод кіл Ейлера - побудова геометричної схеми, що відбиває перетинання або об'єднання множин.
14. 7 Пошук на основі логіки (булева логіку). рішення задачі про вовка, козу і капусту методом пошуку в просторі станів: спробуємо застосувати пропозіціонную логіку (булеву логіку) для знаходження рішення. Позначимо стану вовка, кози, капусти і фермера змінними О, С і Б відповідно і присвоїмо їм значення «істина» або логічна одиниця, якщо вони знаходяться на лівому березі, і «брехня» або 0, якщо на правому. Тоді стартове стан буде "= 1, О = 1, С = 1, Б = 1, а кінцеве -" = 0, О = 0, С = 0, Б = 0.
Забороненими станами будуть наступні: "О-Б - вовк і коза на лівому березі, фермер - на правом; ОС-Б - коза і капуста на лівому березі, фермер - на правом; - "-ПРО - вовк і коза на правому березі, фермер - на лівому; - "-ПРО - коза капуста на правому березі, фермер - на лівому.
Для вирішення цього завдання потрібні вхідні і вихідні змінні. Позначимо "1, О 1, С 1 і Б 1 в якості вихідних змінних. Рішення задачі в логіці першого порядку має виглядати наступним чином: ^, О, С, Е) => (" 1, О 1, С 1, Б 1) = (0, 0 , 0, 0). На жаль, ця задача не вирішується за один крок, тому рішення буде полягати в послідовності перетворень змінних ", О, С, Б в" 1, О 1, С 1, Б 1. При переміщенні з лівого на правий берег не повинні бути істинними вирази "1 О 1 або О 1 С 1. (Б & "&-О-С) => (Б 1 = 0, О 1 = О, С 1 = С) - фермер везе вовка;
(Б 1 = 0, С 1 = 0, " 1 = "" О 1 = О) - фермер везе капусту. Спробуємо тепер виразити у вигляді булевої функції умова переміщення фермера з правого берега на лівий без вантажу. Це можливо в тому випадку, якщо фермер знаходиться на правому березі (-Б), і з його відходом звідти вовк не з'їсть козу (- "-О), а коза - капусту (-О-С): (-Б & - "-О &-О-С) => (" 1 = О, С 1 = С, Б 1 =-Б).
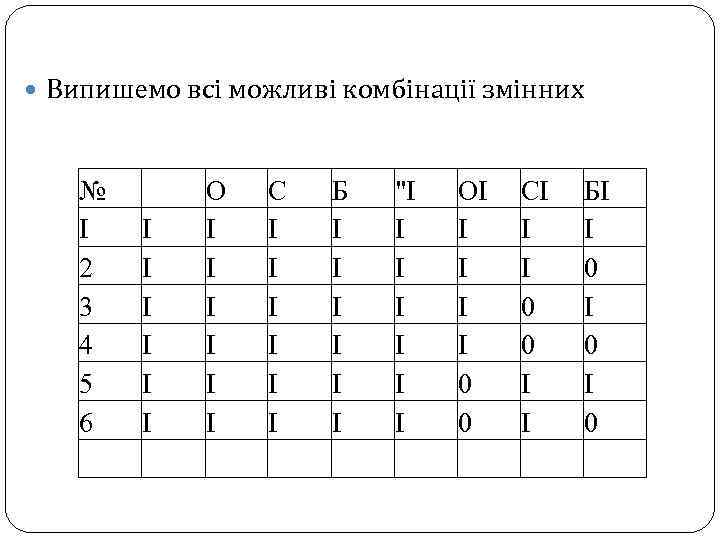Випишемо всі можливі комбінації змінних № І 2 3 4 5 6 І І І О І І І С І І І Б І І І "І І І І ОІ І І 0 0 СІ І І 0 0 І І БІ І 0 І 0
Тепер видалимо з таблиці рядки, відповідні забороненим комбінаціям. До таких відносяться вищеперелічені "ІОІ-РІ, ОЮ-БІ, -" І-ОІРІ, - "І-ОІРІ, а також такі, в яких змінюється стан більш, ніж одній із змінних О, С (за умовою завдання на борт можна взяти більше одного вантажу), або не змінюється стан змінної Б (без човна переправитися не можна), або човен і вантаж рухаються в протилежному напрямку (одна з змінних змінюється з 0 на І, а Б - з І на 0 і навпаки). Також з таблиці можна видалити рядки, що не відповідають кінцевої мети (рух човна порожняком з лівого берега на правий).
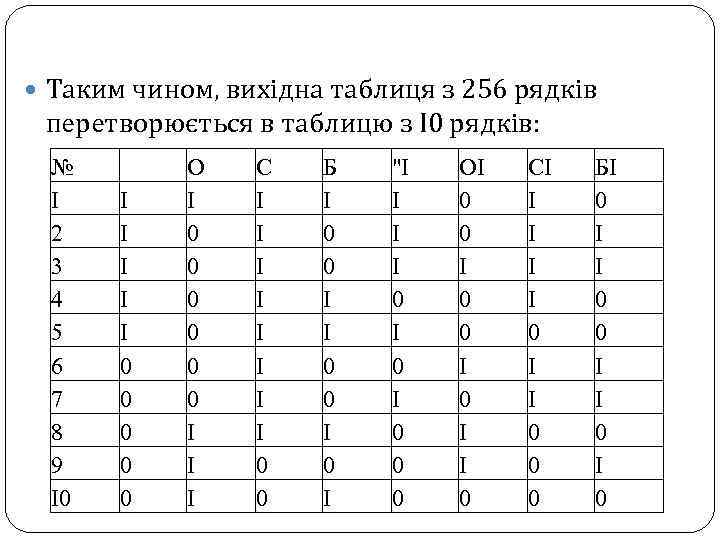Таким чином, вихідна таблиця з 256 рядків перетворюється в таблицю з І0 рядків: № І 2 3 4 5 6 7 8 9 І0 І І І 0 0 0 О І 0 0 0 І І І С І І І І 0 0 Б І 0 0 І 0 І "І І 0 І 0 0 0 ОІ 0 0 І 0 І І 0 СІ І І 0 0 0 БІ 0 І 0
Пошук рішення на основі таблиці істинності полягає в наступному: 1. Знаходимо рядок з вихідним станом змінних (у нашому випадку - перший рядок). 2. отримані оновлені значення змінних "1, 01, С 1 і Б 1 використовуємо для пошуку відповідних значення змінних О, С і Б в таблиці. 3. Пошук закінчується, коли значення "1, 01, С 1 і Б 1 будуть рівні цільовим значенням.
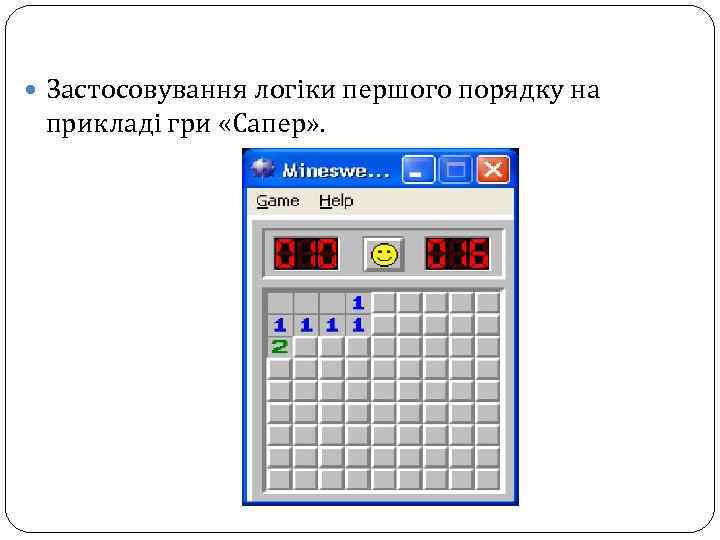Застосовування логіки першого порядку на прикладі гри «Сапер» .
На початку гри ми не володіємо жодною інформацією про розташування мін і перший хід робимо навмання. Якщо у відкритій нами осередку міни немає, то вона відкривається, а на суміжних клітинах відображається інформація про кількість мін у восьми сусідніх клітинах. Запишемо це для комірки (у) у вигляді Кц. Якщо це число дорівнює нулю, то всі сусідні клітини відкриваються автоматично, оскільки тут рішення абсолютно очевидно. Якщо ж N> 0, то потрібно прийняття рішення, яку (які) з сусідніх клітин помітити замінованими.
Слід зазначити, що, поставивши прапорець, ми лише припускаємо, що там знаходиться міна. Дізнатися цей факт точно ми можемо тільки підірвавшись на ній. Тим не менше, ми будемо вважати такий факт встановленим і будемо позначати його Мц = 1. Використовуючи ці позначення ми можемо записати ситуацію після першого кроку розмінування. М 1, 1 = 0; М 1, 2 = 0; Мі = 0; Мм = 0; М 21 = 0; М 22 = 0; М 23 = 0; М 24 = 0; М 31 = 0; N 1, 4 = 1; N 2, 1 = 1; N 2, 2 = 1; N 2, 3 = 1; N 2, 4 = 1; N 3, 1 = 2.
Виходячи з наявних даних ми можемо укласти (будемо позначати резолюції г 1, г 2 і т. д. ): г 1: М 1, 5 / М 2, 5 г 2: М 1, 5 / М 2, 5 / М 3, 3 / М 3, 4 / М 3, 5 г 3: М 3, 2 Г 4: М 3, 2 / М 3, 3 Г 5: М 3 2 / М 3 3 / М 34 Г 6: (М 3, 2 & М 4 2) / (М 41 & М 4 2) / (М 3, 2 / М 41) Можна помітити, що дані вислови некоректними з точки зору булевої алгебри. З г 1 можна укласти, що міна знаходиться або в (1, 5), або в (2, 5), або в обох клітинах. У даній нотації використовуються т. зв. хорновскіе вирази, де диз'юнкція об'єднуються літерали, з яких один і тільки один є істинним. До даних резолюціям може бути застосоване правило поглинання: А & (А / В) = А
Застосовуючи його до резолюцій Г 3, Г 4 та Г 5 отримаємо М 3, 2 = 1, а значить, М 3, 3 = 0, М 3, 4 = 0. Таким чином, ми можемо зробити перший логічний висновок про те, що в клітці (3, 2) знаходиться міна, а в клітинах (3, 3) і (3, 4) їх нема. Додамо ці факт в базу знань про мінному полі, відзначимо міну прапорцем і відкриємо клітини вираження для (3, 3) і (3, 4)
Напишемо хорновскіе отриманої ситуації: гІ: МІ, 5 / М 2, 5 г 2: Мі, 5 / М 2, 5 / Мз, 5 г 3: М 2, 5 / м 3, 5 / М 4 3 / М 44 / М 45 Г 4: М 4, 2 / М 4, и Г 5: М 4, 2 / М 4, 3 / М 4, 4 Застосовуючи правило поглинання до виразів гІ, г 2, г 3, отримаємо: (МІ, 5 / М 2, 5) & (МІ, 5 / М 2, 5 / М 3, 5) = (МІ, 5 / М 2, 5), отже, М 35 = 0, і ми можемо відкрити клітку (3, 5). Після відкриття клітини (3, 5), а потім і (2, 5), отримуємо наступну картину. Мі, 6 / М 2, 6 / М 3, 6 / М 4 4 / М 4 5 / М 4, 6 М 4, 3 / М 4 4 / М 4, 5 М 4, 2 / М 4, и М 4 2 / М 4 3 / М 44
Застосувати правило поглинання тут неможливо, а значить, однозначний висновок про те, яку клітку відкрити, зробити неможливо в силу невизначеності ситуації. Але це не означає, що ми не можемо мінімізувати ризики, розташовуючи даною інформацією.