Литература: 1. Теория механизмов

Литература: 1. Теория механизмов и машин: Учеб. для втузов/ К. В. Фролов С. А. Попов, А. К. Мусатов и др. : Под ред. К. В. Фролова – М. : Высшая школа, 1987. – 496 с. 2. Задания на курсовой проект по теории механизмов и машин/Новосиб. гос. аграр. ун-т: Сост. Евдокимов Ю. И. - Новосибирск, 2008. – 31 с. 3. Теория механизмов и машин. Методические указания к выполнению курсового проекта /Новосиб. гос. аграр. ун-т: Сост. Евдокимов Ю. И. - Новосибирск, 2008. – 58 с. 4. Теория механизмов и машин. Силовой расчёт плоских рычажных механизмов /Новосиб. гос. аграр. ун-т: Сост. Евдокимов Ю. И. - Новосибирск, 2012. – 36 с. 5. Теория механизмов и машин. Силовой расчёт плоских рычажных механизмов/Новосиб. гос. аграр. ун-т: Сост. Евдокимов Ю. И. - Новосибирск, 2012. – 36 с. 6. Лабораторные работы по теории механизмов и машин/Новосиб. гос. аграр. ун-т: Сост. Евдокимов Ю. И. - Новосибирск, 2009. – 40 с. 7. Кинематический анализ плоских рычажных механизмов /Новосиб. гос. аграр. ун-т: Сост. Евдокимов Ю. И. - Новосибирск, 2010. – 27 с. 8. Краткий словарь основных терминов и понятий по теории механизмов и машин/Новосиб. гос. аграр. ун-т: Сост. Евдокимов Ю. И. - Новосибирск, 2011. – 16 с.

Общие сведения • Теория механизмов и машин (ТММ) – наука об общих методах исследования и проектирования механизмов и машин. • Основные проблемы ТММ – анализ и синтез механизмов. • Анализ механизма состоит в исследовании кинематических динамических свойств механизма по заданной его схеме. • Синтез механизма заключается в проектировании схемы механизма по заданным его свойствам.

Разделы курса ТММ: • Структура и классификация механизмов, • Кинематика механизмов, • Динамика механизмов.

СТРУКТУРА МЕХАНИЗМОВ Структура механизмов – один из основных разделов курса «Теория механизмов и машин» , изучающий общие законы строения и классификацию механизмов.

Механизмы состоят из деталей и звеньев, соединённых жёстко или подвижно между собой. Звено механизма – одна или несколько деталей, соединённых жёстко между собой. Примеры: • шатун ДВС в сборе, • поршень, • кривошип (коленчатый вал)

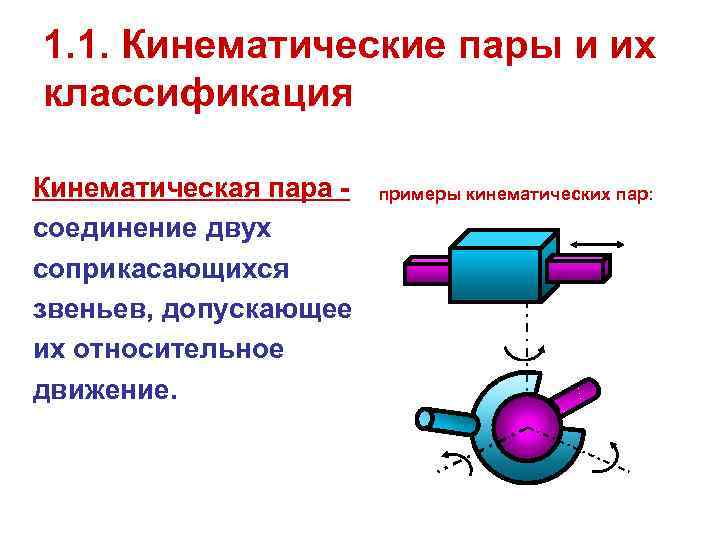
1. 1. Кинематические пары и их классификация Кинематическая пара - примеры кинематических пар: соединение двух соприкасающихся звеньев, допускающее их относительное движение.

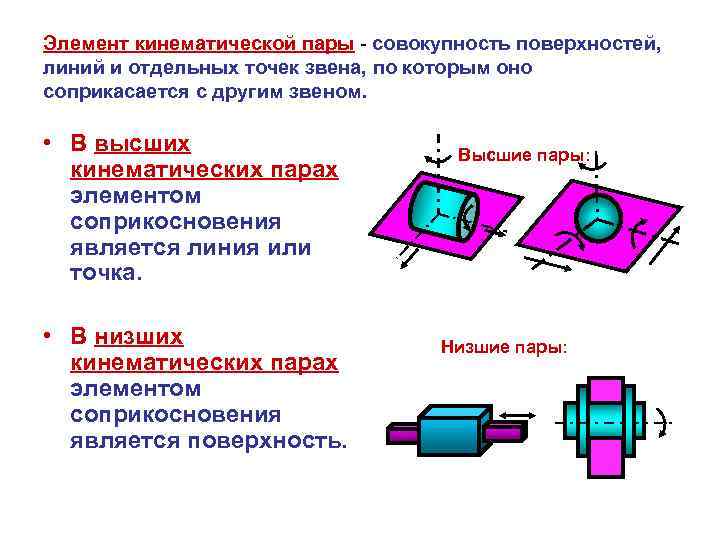
Элемент кинематической пары - совокупность поверхностей, линий и отдельных точек звена, по которым оно соприкасается с другим звеном. • В высших Высшие пары: кинематических парах элементом соприкосновения является линия или точка. • В низших Низшие пары: кинематических парах элементом соприкосновения является поверхность.

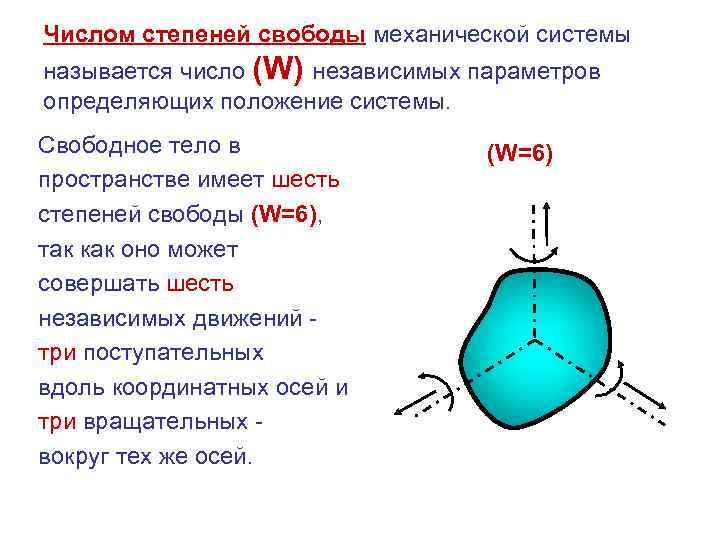
Числом степеней свободы механической системы называется число (W) независимых параметров определяющих положение системы. Свободное тело в (W=6) пространстве имеет шесть степеней свободы (W=6), так как оно может совершать шесть независимых движений - три поступательных вдоль координатных осей и три вращательных - вокруг тех же осей.

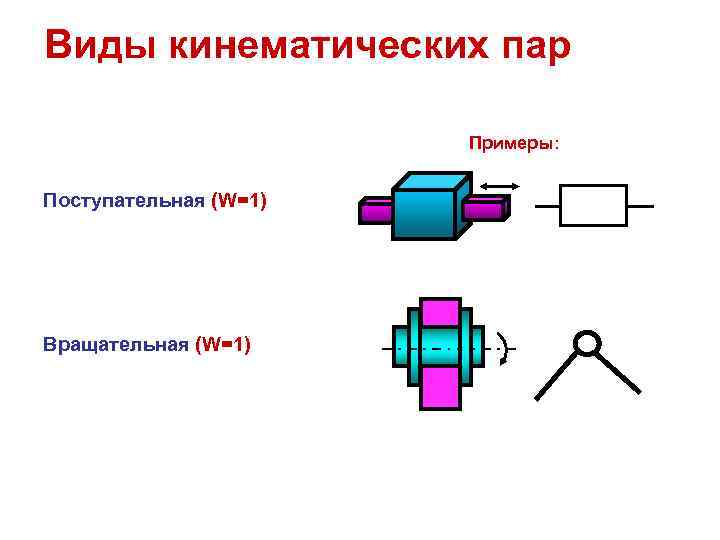
Виды кинематических пар Примеры: Поступательная (W=1) Вращательная (W=1)

Виды кинематических пар Примеры: Винтовая (W=1) Цилиндрическая (W=2)

Виды кинематических пар Примеры: Сферическая с пальцем (W=2) Сферическая (W=3)

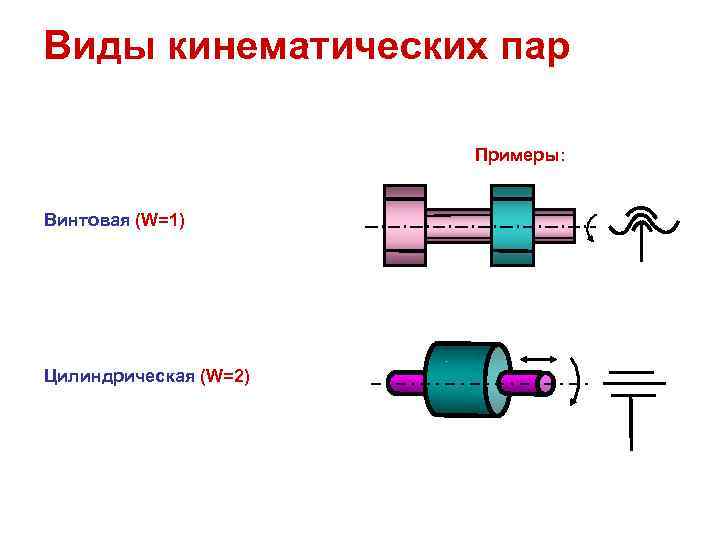
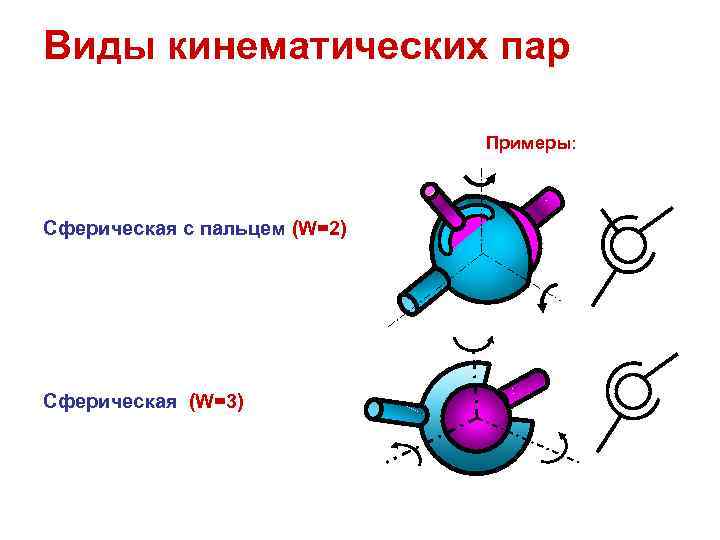
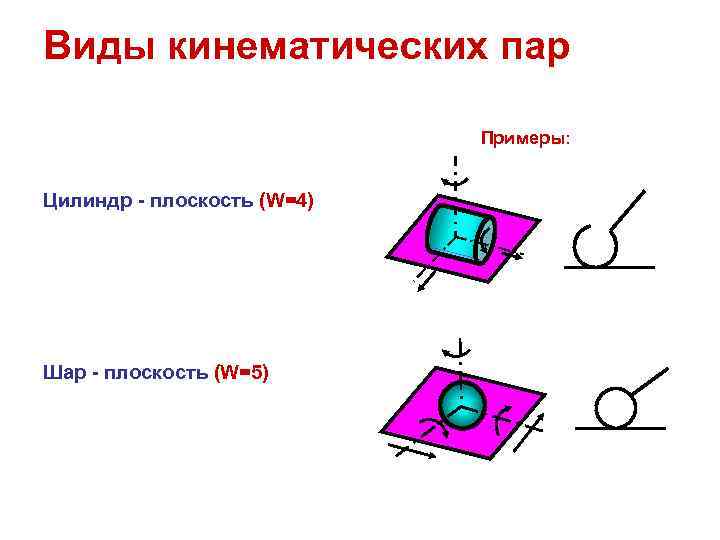
Виды кинематических пар Примеры: Цилиндр - плоскость (W=4) Шар - плоскость (W=5)

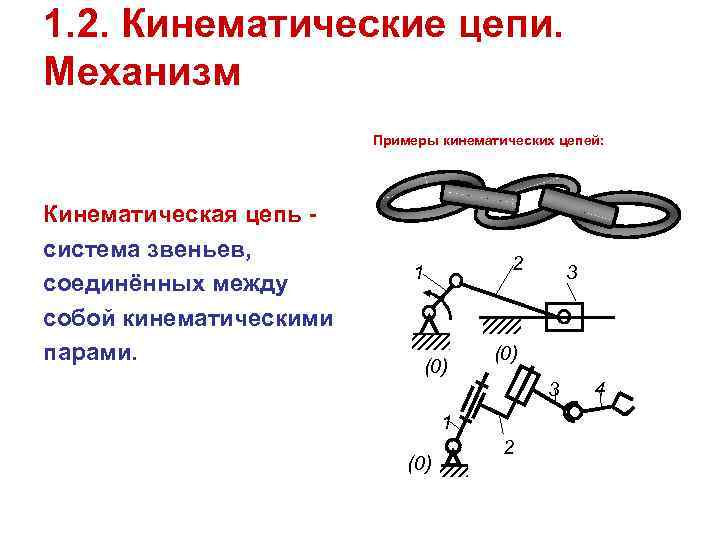
1. 2. Кинематические цепи. Механизм Примеры кинематических цепей: Кинематическая цепь - система звеньев, 1 2 3 соединённых между собой кинематическими парами. (0) 3 4 1 2 (0)

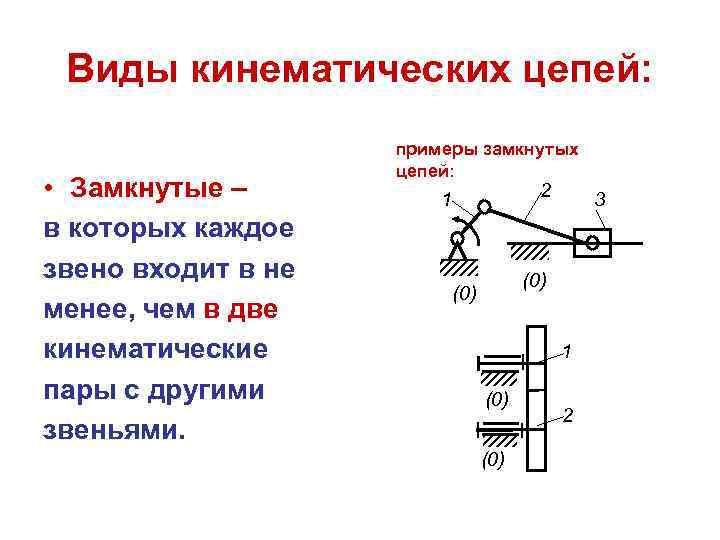
Виды кинематических цепей: примеры замкнутых цепей: • Замкнутые – 1 2 3 в которых каждое звено входит в не (0) менее, чем в две кинематические 1 пары с другими (0) 2 звеньями. (0)

Виды кинематических цепей: пример незамкнутой цепи: • Незамкнутые – у которых имеются 3 4 звенья, входящие 1 только в одну 2 кинематическую пару с другим (0) звеном.

Виды кинематических цепей: • Плоские – Примеры плоских цепей: у которых 1 2 3 траектории движения точек Кривошипно-ползунный (0) механизм всех звеньев находятся в 1 Прямозубая параллельных (0) передача 2 плоскостях. (0)

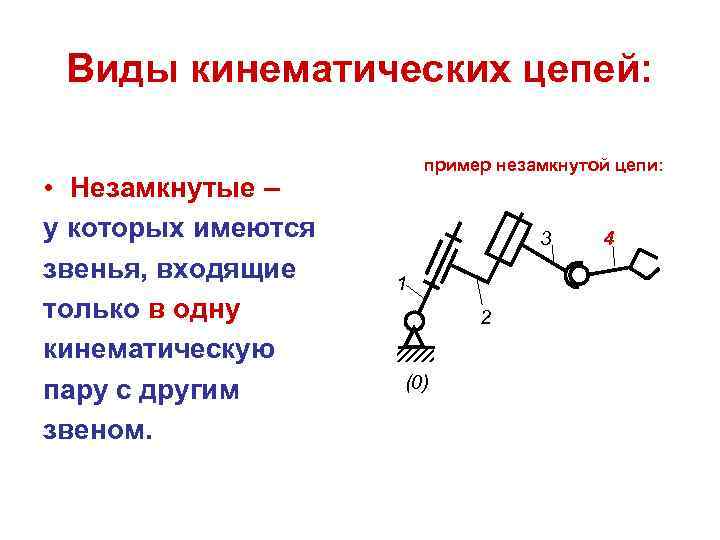
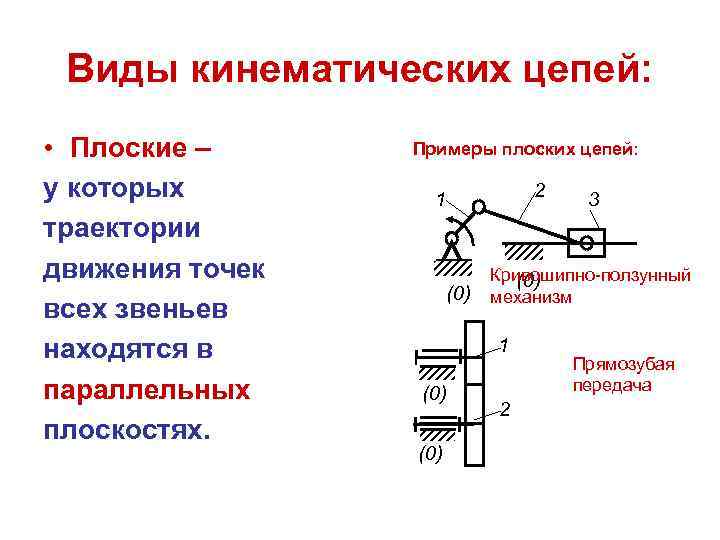
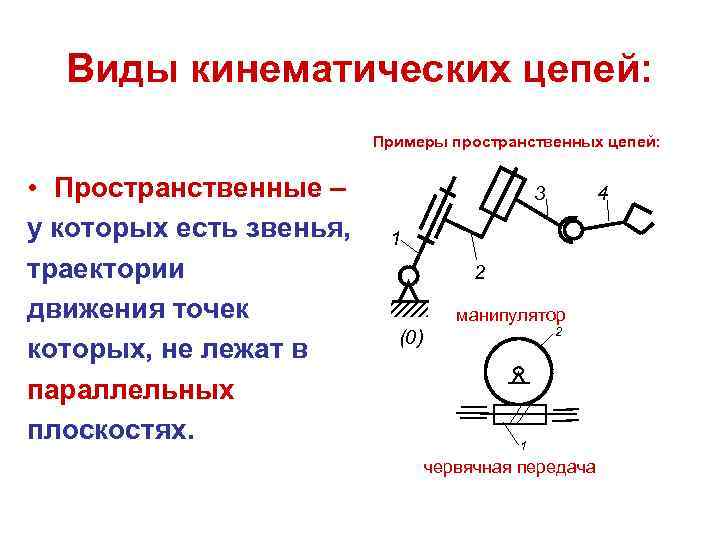
Виды кинематических цепей: Примеры пространственных цепей: • Пространственные – 3 4 у которых есть звенья, 1 траектории 2 движения точек манипулятор 2 (0) которых, не лежат в параллельных плоскостях. 1 червячная передача

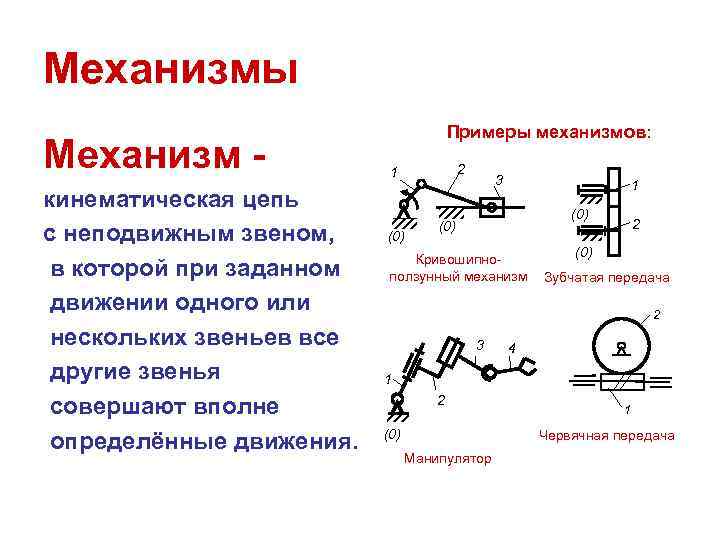
Механизмы Примеры механизмов: Механизм - 1 2 3 1 кинематическая цепь (0) 2 с неподвижным звеном, (0) Кривошипно- в которой при заданном ползунный механизм Зубчатая передача движении одного или 2 нескольких звеньев все 3 4 другие звенья 1 2 совершают вполне 1 (0) определённые движения. Червячная передача Манипулятор

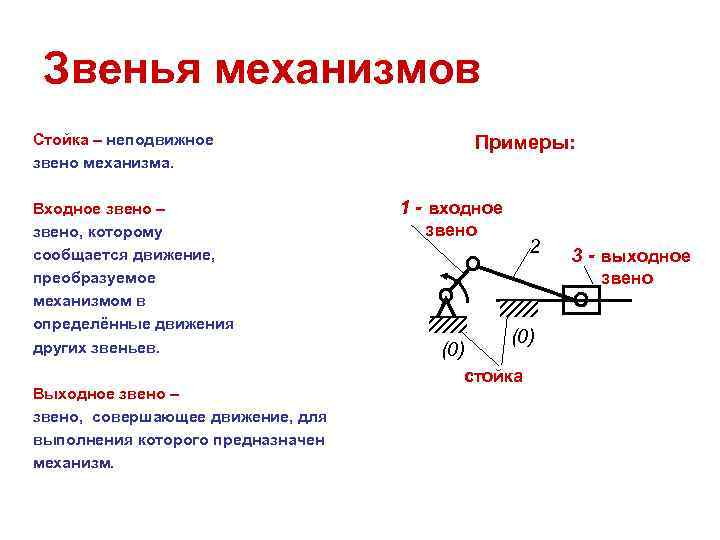
Звенья механизмов Стойка – неподвижное Примеры: звено механизма. Входное звено – 1 - входное звено, которому звено сообщается движение, 2 3 - выходное преобразуемое звено механизмом в определённые движения других звеньев. (0) стойка Выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм.

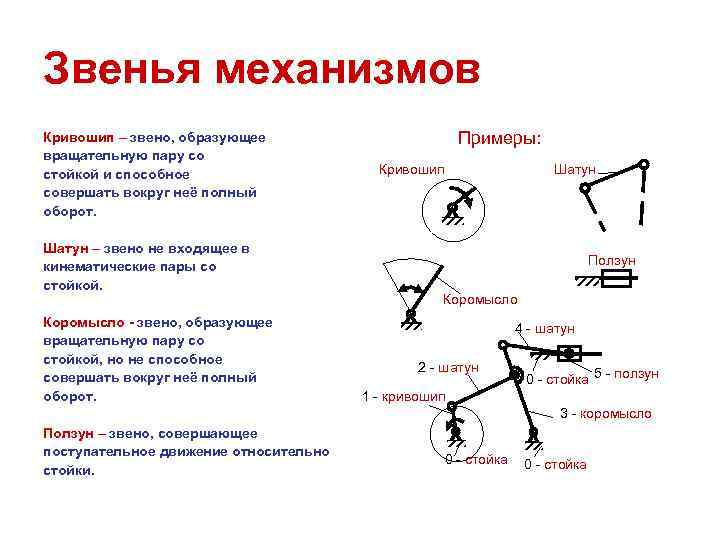
Звенья механизмов Кривошип – звено, образующее Примеры: вращательную пару со стойкой и способное Кривошип Шатун совершать вокруг неё полный оборот. Шатун – звено не входящее в кинематические пары со Ползун стойкой. Коромысло - звено, образующее 4 - шатун вращательную пару со стойкой, но не способное 2 - шатун совершать вокруг неё полный 0 - стойка 5 - ползун оборот. 1 - кривошип 3 - коромысло Ползун – звено, совершающее поступательное движение относительно 0 - стойка стойки.

Механизмы При изображении механизмов на чертежах применяют • структурную (принципиальную) схему с применением условных обозначений без соблюдения размеров звеньев, и • кинематическую схему с соблюдением размеров звеньев, необходимых для кинематического расчёта.

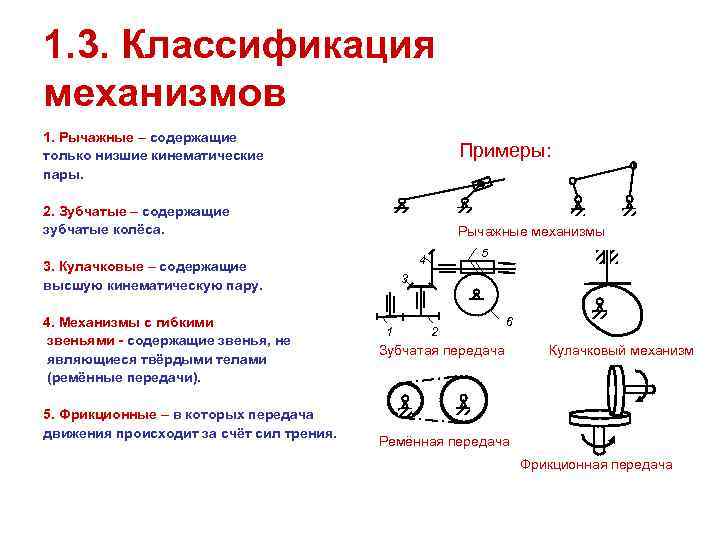
1. 3. Классификация механизмов 1. Рычажные – содержащие только низшие кинематические Примеры: пары. 2. Зубчатые – содержащие зубчатые колёса. Рычажные механизмы 5 4 3. Кулачковые – содержащие 3 высшую кинематическую пару. 4. Механизмы с гибкими 6 1 2 звеньями - содержащие звенья, не Зубчатая передача Кулачковый механизм являющиеся твёрдыми телами (ремённые передачи). 5. Фрикционные – в которых передача движения происходит за счёт сил трения. Ремённая передача Фрикционная передача

1. 4. Число степеней свободы механизма Для пространственных механизмов применяется формула Малышева: W = 6 n – 5 p 1 - 4 p 2 - 3 p 3 - 2 p 4 – p 5 , где n – число подвижных звеньев, p 1 – число одноподвижных (W=1) кинематических пар, p 2 – число двухподвижных (W=2) кинематических пар, p 3 – число трёхподвижных (W=3) кинематических пар, p 4 – число четырёхподвижных (W=4) кинематических пар, p 5 – число пятиподвижных (W=5) кинематических пар. Для плоских механизмов применяется формула Чебышева: W = 3 n – 2 p 1 – p 2.

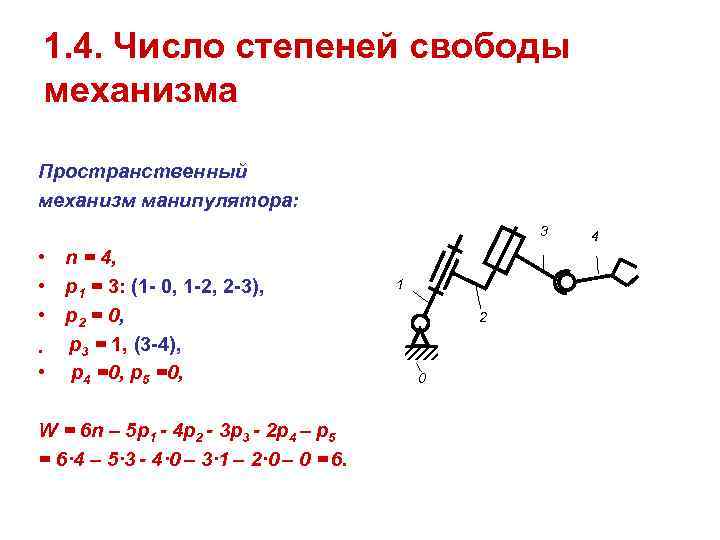
1. 4. Число степеней свободы механизма Пространственный механизм манипулятора: 3 4 • n = 4, • p 1 = 3: (1 - 0, 1 -2, 2 -3), 1 • p 2 = 0, 2 • p 3 = 1, (3 -4), • p 4 =0, p 5 =0, 0 W = 6 n – 5 p 1 - 4 p 2 - 3 p 3 - 2 p 4 – p 5 = 6· 4 – 5· 3 - 4· 0 – 3· 1 – 2· 0 – 0 = 6.

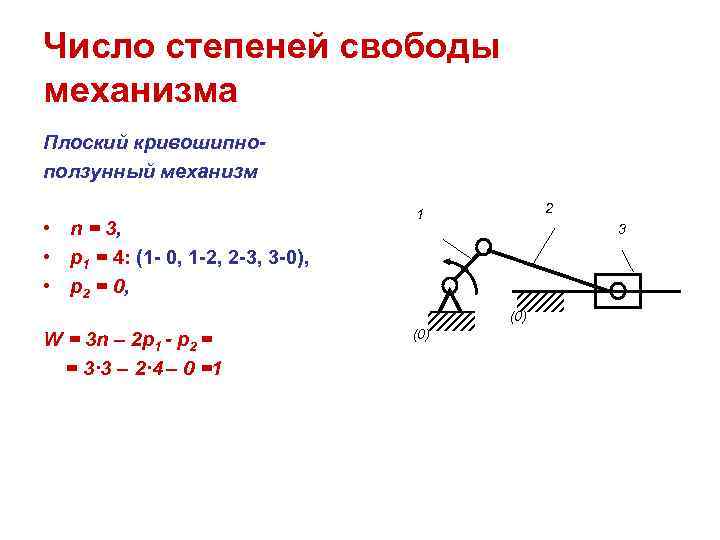
Число степеней свободы механизма Плоский кривошипно- ползунный механизм 1 2 • n = 3, 3 • p 1 = 4: (1 - 0, 1 -2, 2 -3, 3 -0), • p 2 = 0, (0) W = 3 n – 2 p 1 - p 2 = (0) = 3· 3 – 2· 4 – 0 =1

Число степеней свободы механизма Плоский зубчатый механизм 1 • n = 2, • p 1 = 2: (1 - 0, 2 -0), (0) • p 2 = 1: (1 -2) 2 W = 3 n – 2 p 1 - p 2 = (0) = 3· 2 – 2· 2 – 1 = 1

1. 5. Структурный анализ и синтез плоских рычажных механизмов ЛЕОНИД ВЛАДИМИРОВИЧ АССУР (1878 – 1920), русский учёный, один из основателей отечественной научной школы по теории механизмов и машин. Создал рациональную классификацию плоских рычажных механизмов.

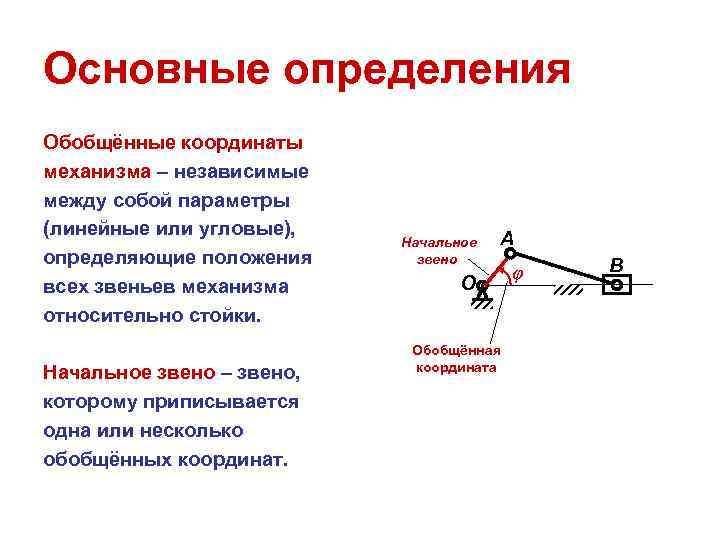
Основные определения Обобщённые координаты механизма – независимые между собой параметры (линейные или угловые), А Начальное определяющие положения звено В φ всех звеньев механизма О относительно стойки. Обобщённая координата Начальное звено – звено, которому приписывается одна или несколько обобщённых координат.

Принцип Ассура Образование сложных плоских рычажных механизмов осуществляется присоединением одной или нескольких структурных групп (групп Ассура) к начальному звену и стойке.

Структурные группы Структурная группа (группа Ассура) – элементарная кинематическая цепь, число степеней свободы которой относительно её внешних пар равно нулю. W = 3 n – 2 p 1 – p 2 = 0. Так как в группах Ассура p 2 =0, то p 1 = (3/2)n.

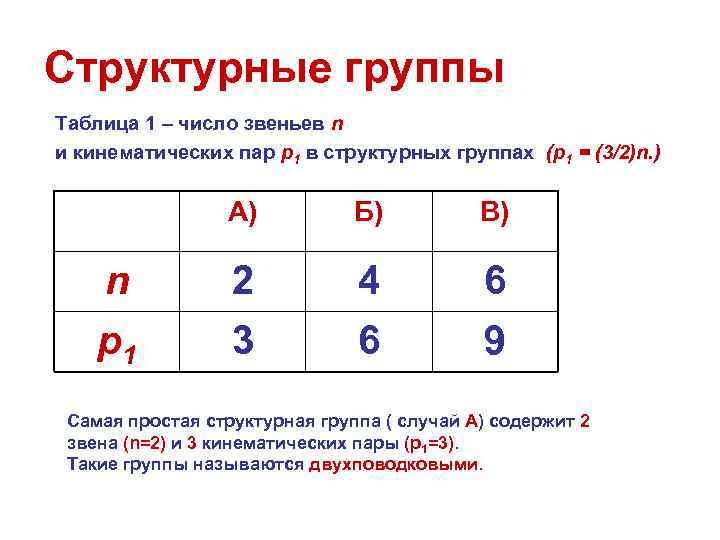
Структурные группы Таблица 1 – число звеньев n и кинематических пар p 1 в структурных группах (p 1 = (3/2)n. ) А) Б) В) n 2 4 6 p 1 3 6 9 Самая простая структурная группа ( случай А) содержит 2 звена (n=2) и 3 кинематических пары (p 1=3). Такие группы называются двухповодковыми.

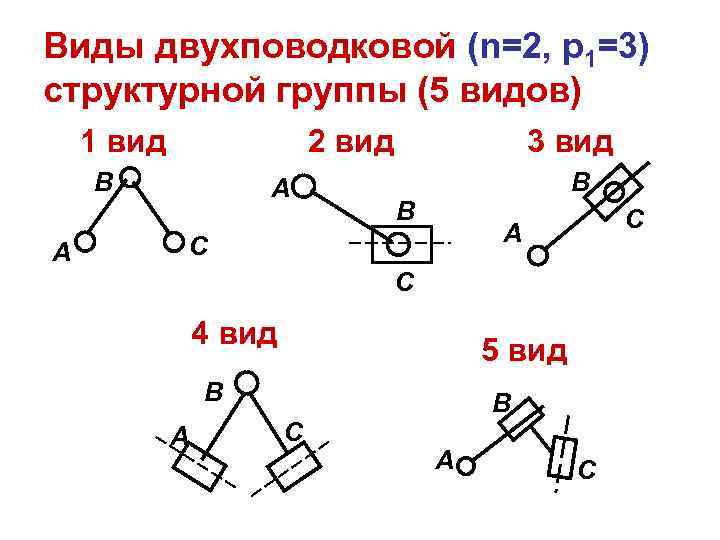
Виды двухповодковой (n=2, p 1=3) структурной группы (5 видов) 1 вид 2 вид 3 вид В А В С А А С С 4 вид 5 вид В А С А С

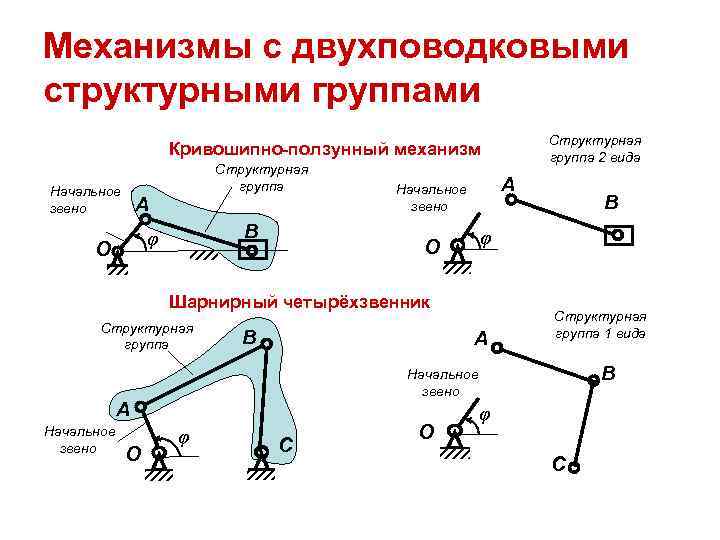
Механизмы с двухповодковыми структурными группами Структурная Кривошипно-ползунный механизм группа 2 вида Структурная Начальное группа Начальное А звено А звено В φ В φ О Шарнирный четырёхзвенник Структурная группа 1 вида группа В А Начальное В звено А φ Начальное φ О звено О С С

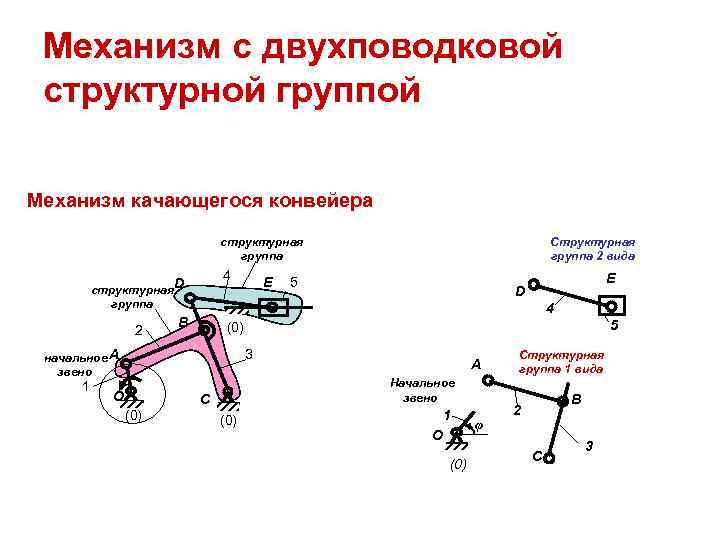
Механизм с двухповодковой структурной группой Механизм качающегося конвейера структурная Структурная группа 2 вида 4 Е 5 структурная D группа 4 В (0) 5 2 начальное А 3 Структурная А группа 1 вида звено 1 Начальное О С звено В (0) 1 2 (0) φ О 3 С (0)

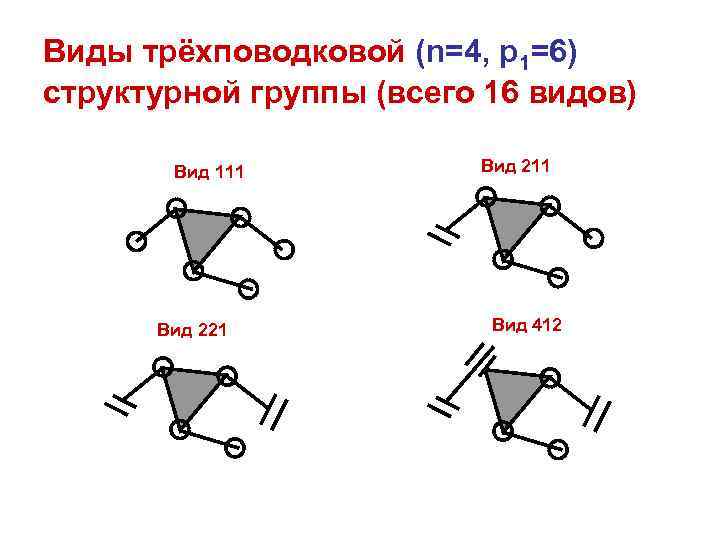
Виды трёхповодковой (n=4, p 1=6) структурной группы (всего 16 видов) Вид 111 Вид 221 Вид 412

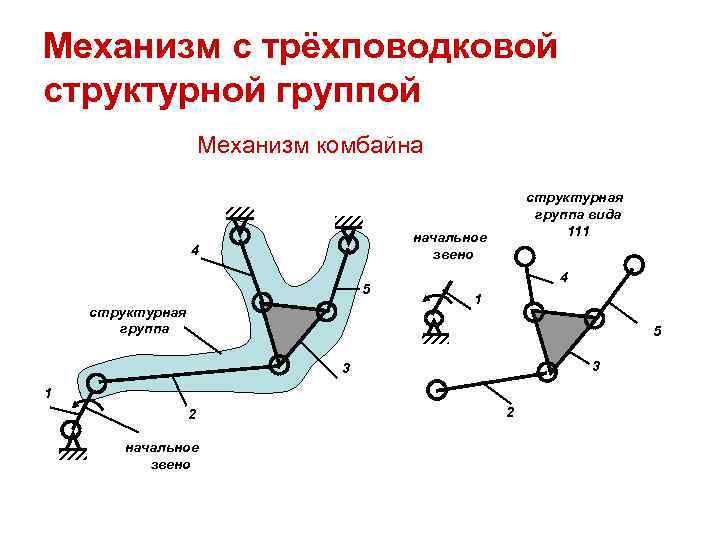
Механизм с трёхповодковой структурной группой Механизм комбайна структурная группа вида начальное 111 4 звено 4 5 1 структурная группа 5 3 1 2 начальное звено

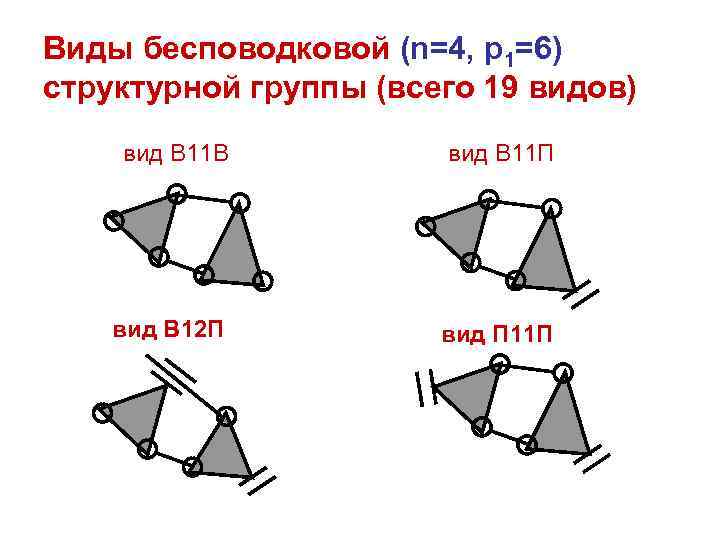
Виды бесповодковой (n=4, p 1=6) структурной группы (всего 19 видов) вид В 11 В вид В 11 П вид В 12 П вид П 11 П

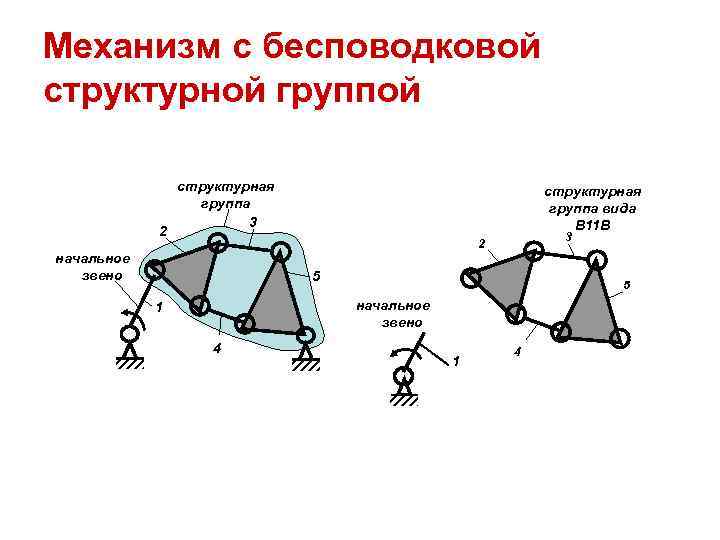
Механизм с бесповодковой структурной группой структурная группа вида 3 В 11 В 2 3 2 начальное звено 5 1 начальное звено 4 1

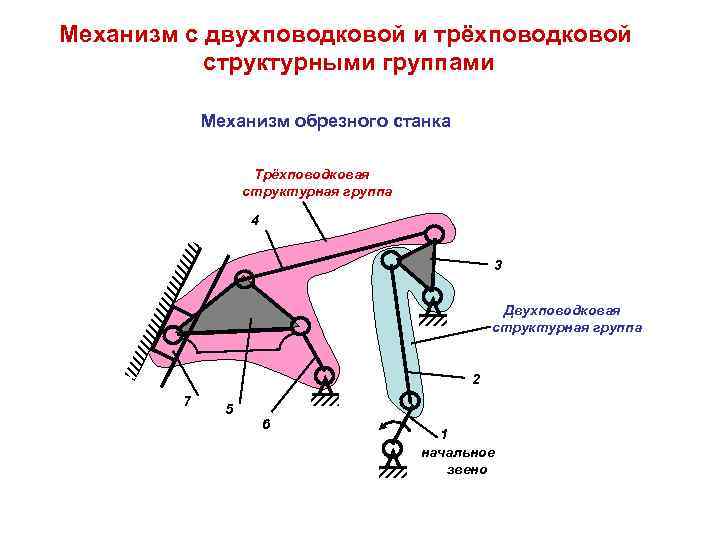
Механизм с двухповодковой и трёхповодковой структурными группами Механизм обрезного станка Трёхповодковая структурная группа 4 3 Двухповодковая структурная группа 2 7 5 6 1 начальное звено