ЛІТЕРАТУРА 1 Гловацкая А П Методы и алгоритмы

ЛІТЕРАТУРА 1. Гловацкая А. П. Методы и алгоритмы вычислительной математики. М. : Радио и связь. – 1999. – 408 с. 2. Данилина Н. И. , Дубровская Н. С. , Кваша О. П. Численные методы. - М. : Высшая школа, 1976. 3. Демидович Б. П. , Марон И. А. Основы вычислительной математики. - М. : Наука, 1970 - 664 с. 4. Копченова Н. В. , Марон И. А. Вычислительная математика в примерах и задачах. М. : Наука. – 1972. – 366 с. 5. Лященко М. Я. , Головань М. С. Чисельні методи. – Київ: Либідь. – 1996. – 288 с. 6. Ортега Д. , Пул У. Введение в численные методы решения дифференциальных равнений. -М. : Наука, 1986. - 288 с. 7. Самарский А. А. Введение в численные методы. - М. : Наука, 1982 - 272 с. 8. Турчак Л. И. Основы численных методов. М. : Наука. – 1987. – 318 с. 9. Фельдман Л. П. , Петренко А. І. , Дмитрієва О. А. Чисельні методи в інформатиці. - Київ: Видавнича група BHV. - 2006. – 480 с.

ОБЧИСЛЮВАЛЬНИЙ ЕКСПЕРИМЕНТ ТА ЙОГО ЕТАПИ Обчислювальний експеримент — це метод дослідження складних процесів, об'єктів чи систем шляхом побудови , реалізації та аналізу їх математичних моделей засобами обчислювальної техніки. Під математичною моделлю фізичної системи, об'єкта або процесу розуміють сукупність математичних співвідношень (формул, рівнянь, логічних виразів), які визначають характеристики стану і властивості системи, об'єкта і процесу та їх функціонування залежно від параметрів їх компонентів, початкових умов, вхідних збуджень і часу. Чисельні методи — це математичний інструментарій, за допомогою якого математична задача формулюється так, щоб вона могла бути розв’язана за допомогою простих арифметичних і логічних операцій, таких звичних для комп'ютера. В цьому випадку говорять про перетворення математичної задачі в обчислювальну задачу. При цьому послідовність виконання необхідних арифметичних і логічних операцій визначається алгоритмом її розв’язку.

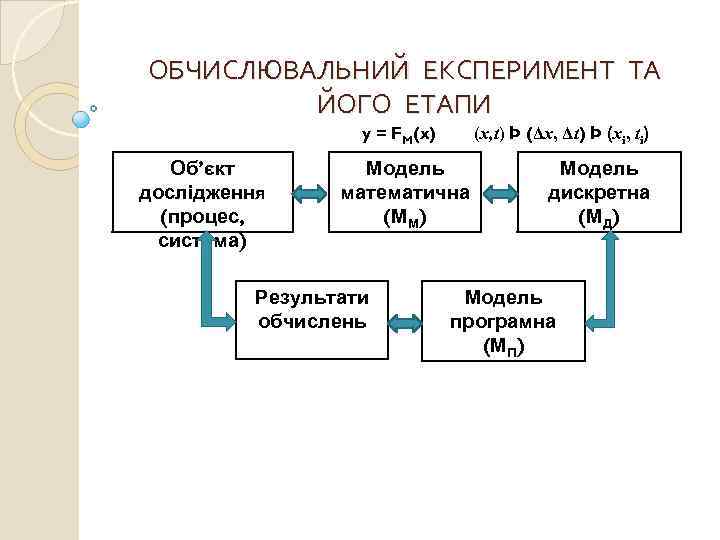ОБЧИСЛЮВАЛЬНИЙ ЕКСПЕРИМЕНТ ТА ЙОГО ЕТАПИ y = FM(x) Об’єкт дослідження (процес, система) (x, t) Þ (Δx, Δt) Þ (xi, ti) Модель математична (ММ) Результати обчислень Модель дискретна (МД) Модель програмна (МП)

ВЛАСТИВОСТІ ЧИСЕЛЬНИХ МЕТОДІВ 1. Передбачають проведення великої кількості арифметичних обчислень за допомогою рекурсивних співвідношень, що використовуються для організації ітерацій, тобто повторюваних циклів обчислень із зміненими початковими умовами для поліпшення розв’язку. 2. Направлені на локальне спрощення задачі, коли, наприклад, нелінійні залежності чи функції лінеаризуються за допомогою своїх обчислених похідних або похідні замінюються різницевими апроксимаціями (наприклад, ряд Тейлора чи поліноміальні апроксимації). 3. Залежать від вибору початкового значення (або декількох), необхідного для початку обчислень, від властивостей нелінійних функцій, що використовуються в математичних моделях.

ВЛАСТИВОСТІ ЧИСЕЛЬНИХ МЕТОДІВ Чисельні методи характеризуються різною: § швидкістю збіжності, тобто числом ітерацій, виконання яких необхідне для отримання заданої точності розв’язку; § стійкістю, тобто збереженням достовірності розв’язку при подальших ітераціях; § точністю отримуваного розв’язку при виконанні однакового числа ітерацій або циклів обчислень. Чисельні методи розрізняються за рівнем: § універсальності для розв’язування різних математичних задач; § складності їх програмування; § чутливості до погано обумовлених (або некоректних) математичних задач.

ОСНОВНІ ЗАДАЧІ ЧИСЕЛЬНИХ МЕТОДІВ 1. Розв’язування системи лінійних (в загальному випадку, лінеаризованих) рівнянь. 2. Розв’язування систем нелінійних рівнянь. 3. Проблема власних значень матриці. 4. Наближення масиву даних або складної функції набором стандартних, більш простих функцій. 5. Чисельне інтегрування і диференціювання. 6. Розв’язування систем звичайних диференціальних рівнянь та диференціальних рівнянь в частинних похідних. 7. Розв’язування інтегральних рівнянь. 8. Чисельна оптимізація.

ВИМОГИ ДО ЧИСЕЛЬНИХ МЕТОДІВ Вимоги до засобів реалізації чисельних методів: • швидкодія; • об’єм пам’яті; • можливість тестування; • аналіз критичних ситуацій; • документованість; • супроводження; • можливість перенесення на інші комп’ютерні платформи. Вимоги до адекватності обчислювальної задачі: • збіжність; • стійкість; • коректність.

ВИМОГИ ДО ЧИСЕЛЬНИХ МЕТОДІВ Метод є збіжним, якщо виконується умова: Розв’язок є стійким стосовно вхідних даних, якщо він неперервно залежить від вхідних даних, тобто для задачі маємо Обчислювальна задача y = A(x) називається коректною, якщо для будьяких вхідних даних, що належать певному класу, існує розв’язок задачі , який є єдиним і стійким стосовно вхідних даних, де A(x) – оператор (алгоритм), що реалізує метод обчислень. Застосовувати ЧМ безпосередньо до некоректних задач не можна.

ПОХИБКИ ОБЧИСЛЕНЬ Поліном Уілкінсона: Якщо внести незначну помилку в коефіцієнт а 19 = 210 (210 + 2 - 23) = 210, 000 119, то серед коренів, знайдених по коефіцієнтах полінома, з'являться комплексні корені xi, i + 1 = 16, 730737400 ± j 2, 812624894.

ПОХИБКИ ОБЧИСЛЕНЬ Існують декілька джерел похибок обчислень: 1. Похибки вхідних даних і спрощення моделей компонентів. 2. Округлення під час обчислень, локальні відсікання. 3. Похибки представлення чисел в комп'ютері. Нехай а — точне значення величини; — наближене значення цієї величини, тоді — абсолютна похибка; — відносна похибка.

ПОХИБКИ ОБЧИСЛЕНЬ При виконанні арифметичних операцій похибки обчислень тільки накопичуються, незалежно від типу виконуваної операції:

ОЦІНКА СКЛАДНОСТІ АЛГОРИТМІВ І ОБЧИСЛЕНЬ Складність обчислень, передбачених алгоритмом, оцінюється за допомогою сигнальних функцій f. A(n), які визначають обчислювальні витрати на роботу алгоритму через кількість необхідних операцій, що використовується алгоритмом в процесі обчислень, де f. A (n) — верхня межа кількості операцій; n — розмірність задачі.

ОЦІНКА СКЛАДНОСТІ АЛГОРИТМІВ І ОБЧИСЛЕНЬ 1. Поліноміальний алгоритм, сигнальна функція якого f. A (n) росте від n не швидше, ніж деякий поліном g(n). При цьому розрізняють оцінки двох типів: f. A (n) = O [g(n)] і f. A (n) = о [g(n)] 2. Комбінаторний алгоритм, коли сигнальна функція f. A(n) змінюється як експоненціальна функція або містить в собі оцінки операцій перебору, сполучень, визначення факторіалу n! Для виконання n! = 20! (24 329 *1017) операцій для комп’ютера з середнім часом виконання операції 10 -7 сек необхідно близько 77 століть.