Литература 1. 2. 3. 4. 5. Василевич Л.

Литература 1. 2. 3. 4. 5. Василевич Л. Ф. Теория игр. - КИИМ, 2000. Печерский С. Л. , Беляева А. А. Теория игр для экономистов. Вводный курс. Данилов В. И. Лекции по теории игр. – М. , 2002. Воробьев Н. Н. Теория игр для экономистов-кибернетиков. – М. : Наука, 1985. Мулен Э. Теория игр с примерами из математической экономики. – М. : Мир, 1985

Введение в теорию игр «Что наша жизнь? – Игра. » А. С. Пушкин «Пиковая дама»

Основные понятия ТИ Игра – математическая модель конфликтной ситуации; Игроки – стороны, участвующие в конфликте; Выигрыш – исход конфликта, характеризующий игру с количественной стороны; Стратегия игрока – совокупность правил (программ действий), определяющих поведение игрока на каждом ходе в зависимости от сложившейся в игре ситуации

Определение теории игр Теория игр - это математическая теория конфликтных ситуаций. Цель теории игр - выработка рекомендаций по разумному поведению участников конфликта (определение оптимальных стратегий поведения игроков).

Виды стратегий Чистая – стратегия, которую выбирают неслучайным образом. Смешанная – набор стратегий, которые рекомендуется выбирать игроку случайным образом в зависимости от ситуации. Активная – стратегия, входящая в смешанную стратегию. Оптимальная стратегия – такая стратегия, которая при многократном повторении игры обеспечивает максимальный средний выигрыш (минимальный средний проигрыш).

Решение игры оптимальные стратегии каждого из игроков (смешанные или чистые); ¡ цена игры – выигрыш игрока, полученный в зависимости от набора оптимальных стратегий. Цель решения игры – определение оптимальных стратегий и цены игры. ¡

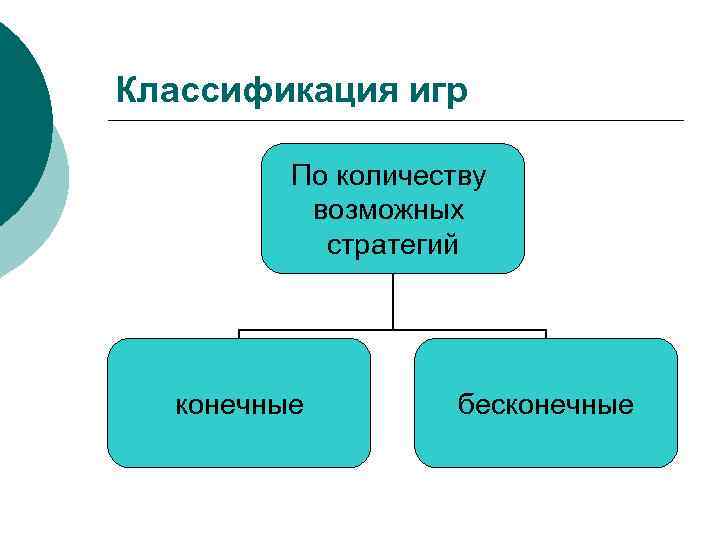Классификация игр По количеству возможных стратегий конечные бесконечные

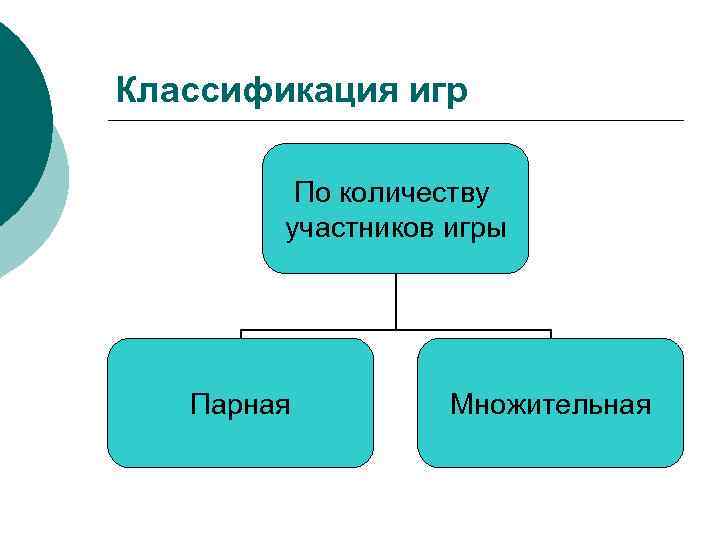Классификация игр По количеству участников игры Парная Множительная

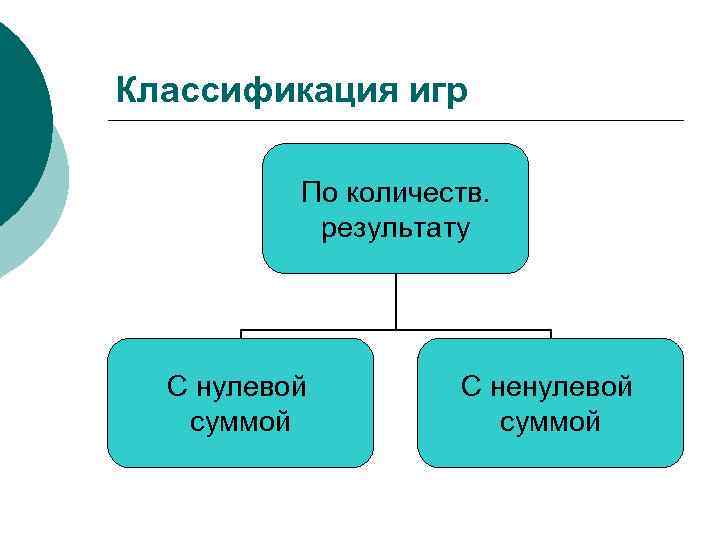Классификация игр По количеств. результату С нулевой суммой С ненулевой суммой

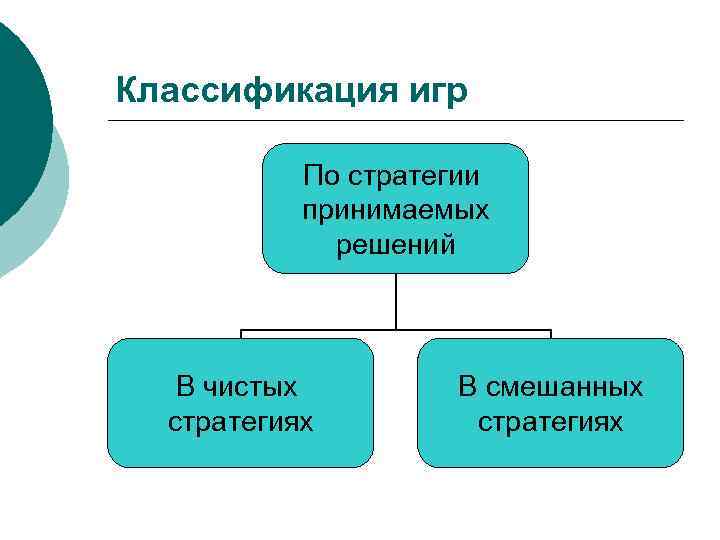Классификация игр По стратегии принимаемых решений В чистых стратегиях В смешанных стратегиях

Антагонистические игры и методы их решения

Антагонистическая игра ¡ ¡ ¡ Конечная парная игра с нулевой суммой является антагонистической, так как выигрыш одного игрока равен проигрышу второго, а следовательно цели этих игроков прямо противоположны. Такая игра описывается платежной матрицей, в которой задаются выигрыши первого игрока (они же являются проигрышами второго игрока). Антагонистическая игра называется также матричной игрой.

Пример 1. Правила игры: Игрок А выкладывает монету на стол; Игрок В угадывает ее верхнюю сторону. Если В угадывает – получает от А 1 очко, Не угадывает – уплачивает штраф 1 очко в пользу А. Построить платежную матрицу игры.

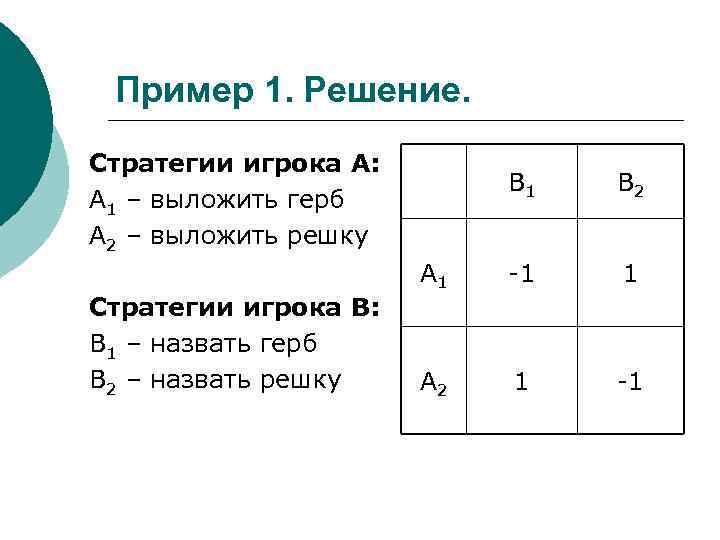Пример 1. Решение. Стратегии игрока А: А 1 – выложить герб А 2 – выложить решку Стратегии игрока В: В 1 – назвать герб В 2 – назвать решку В 1 В 2 А 1 -1 1 А 2 1 -1

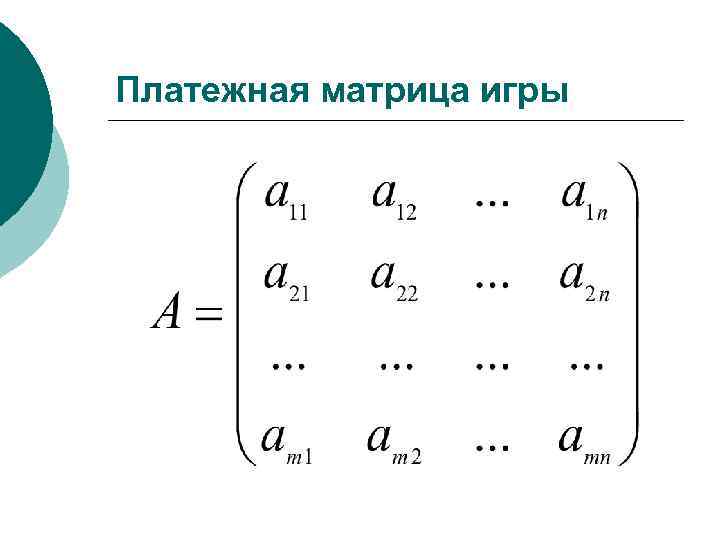Платежная матрица игры

Дополнительные условия Цель игрока А – получить наибольший выигрыш; Цель игрока В – получить наименьший проигрыш.

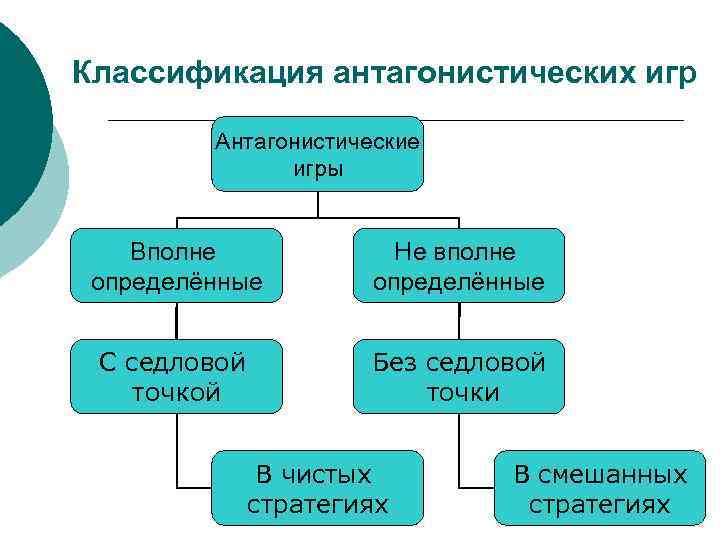Классификация антагонистических игр Антагонистические игры Вполне определённые Не вполне определённые С седловой точкой Без седловой точки В чистых стратегиях В смешанных стратегиях

Игры с седловой точкой

Верхняя и нижняя границы игры С позиции игрока А: 1) Минимумы по строкам αi=min aij; 2) Игрок А выберет стратегию, чтобы α=max αi α=max (min aij) – гарантированный выигрыш – нижняя граница игры ¡ С позиции игрока В: 1) Максимумы по столбцам βi=max aij; 2) Игрок В выберет стратегию, чтобы β =min βi β = min (max aij) – наибольший проигрыш – верхняя граница игры ¡

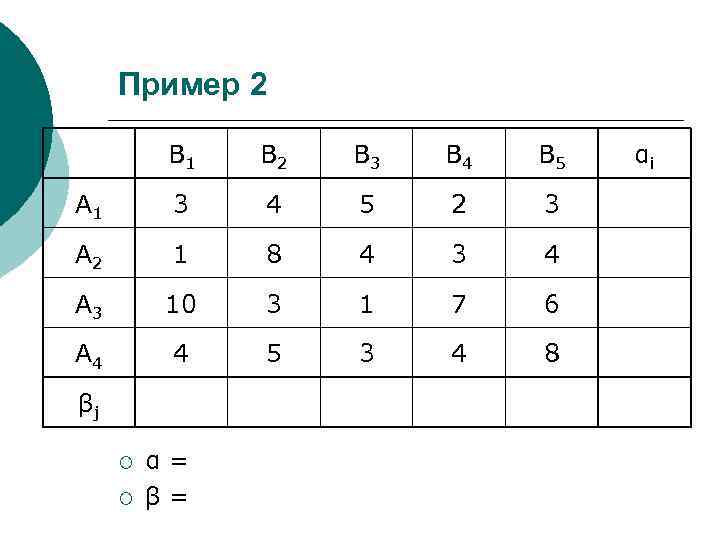Пример 2 B 1 B 2 B 3 B 4 B 5 А 1 3 4 5 2 3 А 2 1 8 4 3 4 А 3 10 3 1 7 6 А 4 4 5 3 4 8 βj ¡ ¡ α= β= αi

Игра с седловой точкой Если α = β, ¡ то минимаксы Аi и Вj будут устойчивыми; ¡ пара (Аi ; Вj) называется седловой точкой; цена игры ν = α = β; ¡ решение игры - (Аi 0 ; Вj 0; ν) ¡

Задача 1. B 1 B 2 B 3 B 4 А 1 2 4 7 5 А 2 7 6 8 7 А 3 5 3 4 1 βj ¡ α= ; β= ; ¡ Решение игры: (А ; В ; ν = ) αi

Игры без седловой точки

Смешанная стратегия набор чистых стратегий с указанными вероятностями их применения в игре. ¡ Общий вид: ¡ Краткая форма:

Зависимости строк (столбцов) ¡ ¡ ¡ Стратегия Аk называется доминирующей над стратегией Ар, если все выигрыши в строке Аk не меньше соответствующих выигрышей в строке Ар. Стратегия Вk называется доминирующей над стратегией Вр, если все проигрыши в столбце Вk не больше соответствующих проигрышей в столбце Вр. Две стратегии называются дублирующими, если все соответствующие выигрыши (проигрыши) одинаковы.

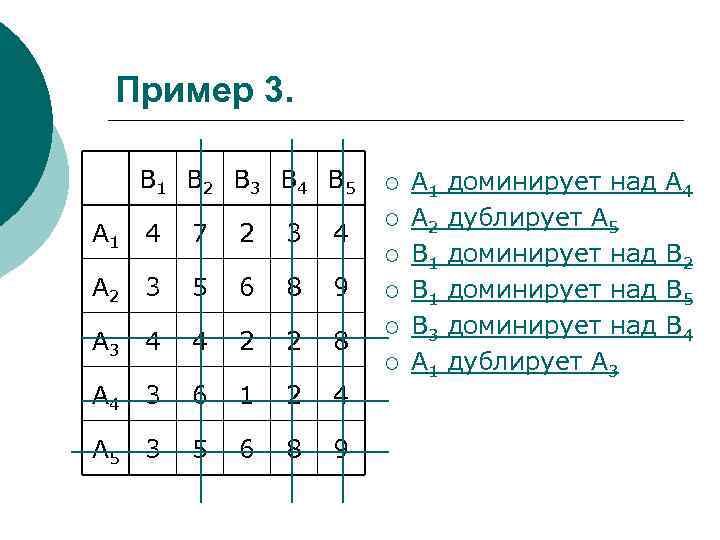Пример 3. B 1 B 2 B 3 B 4 B 5 А 1 4 7 2 3 4 А 2 3 5 6 8 9 А 3 4 4 2 2 8 А 4 3 6 1 2 4 А 5 3 5 6 8 9 ¡ ¡ ¡ А 1 А 2 В 1 В 3 А 1 доминирует над дублирует А 5 доминирует над дублирует А 3 А 4 В 2 В 5 В 4

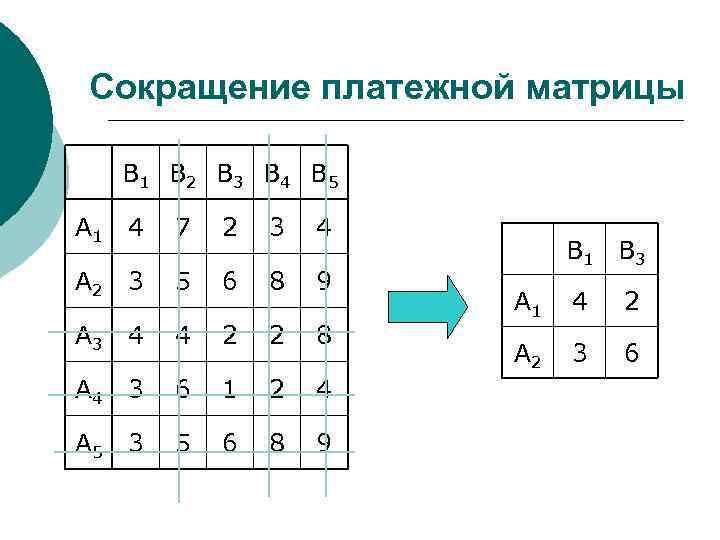Сокращение платежной матрицы B 1 B 2 B 3 B 4 B 5 А 1 4 7 2 3 4 А 2 3 5 6 8 9 А 3 4 4 2 2 8 А 4 3 6 1 2 4 А 5 3 5 6 8 9 B 1 B 3 А 1 4 2 А 2 3 6

Графический метод решения игр Применяется для ¡ Игр без седловой точки ¡ Игр, в которых хотя бы один игрок имеет только две активные стратегии (размерность платежной матрицы 2×n или m× 2)

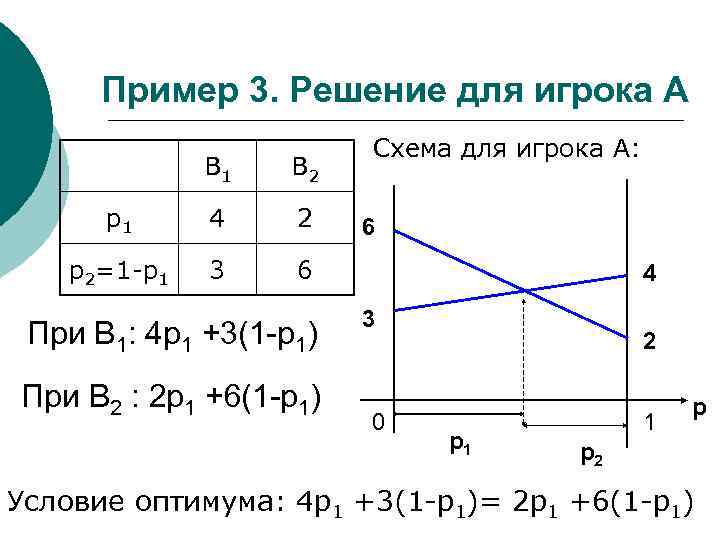Пример 3. Решение для игрока А В 1 В 2 р1 4 2 р2=1 -р1 3 Схема для игрока А: 6 При В 1: 4 р1 +3(1 -р1) При В 2 : 2 р1 +6(1 -р1) 6 4 3 0 2 р1 1 р р2 Условие оптимума: 4 р1 +3(1 -р1)= 2 р1 +6(1 -р1)

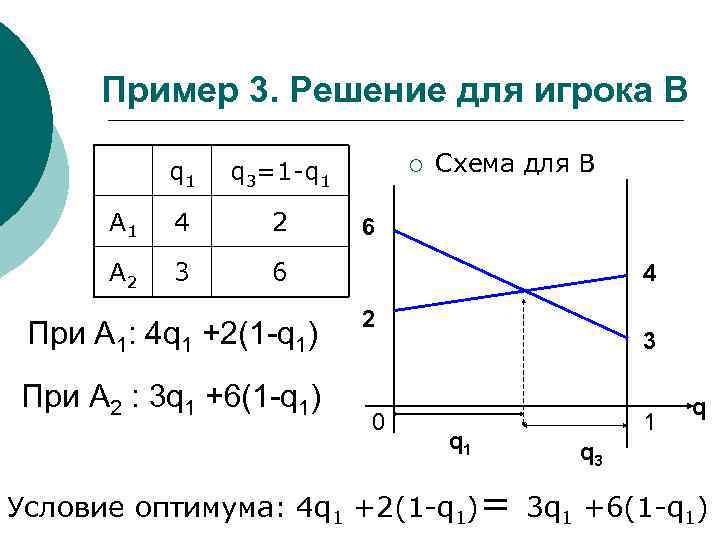Пример 3. Решение для игрока B q 1 q 3=1 -q 1 A 1 4 2 A 2 3 Схема для В 6 При А 1: 4 q 1 +2(1 -q 1) При A 2 : 3 q 1 +6(1 -q 1) ¡ 6 4 2 0 3 q 1 1 q q 3 Условие оптимума: 4 q 1 +2(1 -q 1)= 3 q 1 +6(1 -q 1)

Пример 3. Решение ¡ Найдём значения p 1 и q 1, решая уравнения: 4 р1 +3(1 -р1)= 2 р1 +6(1 -р1) ~ p 1=0. 6 ~ p 2=0. 4 4 q 1 +2(1 -q 1)= 3 q 1 +6(1 -q 1) ~ q 1=0. 8 ~ q 3=0. 2 ¡ ¡ Найдём цену игры, подставляя найденные значения р или q в любое из выражений: ν=4*0, 6+3*0, 4=3, 6 Ответ (в полной игре): SA 0=(0. 6, 0. 4, 0, 0, 0); SB 0=(0. 8, 0, 0. 2, 0, 0); ν=3. 6

Решение игр 2×n или m× 2 Такие игры сводятся к играм 2 х2, т. к. их решение содержит не более двух активных стратегий для каждого из игроков. ¡ Найти активные стратегии можно графическим методом, выбирая линии выигрышей, пересекающиеся в точке максимума (минимума). ¡

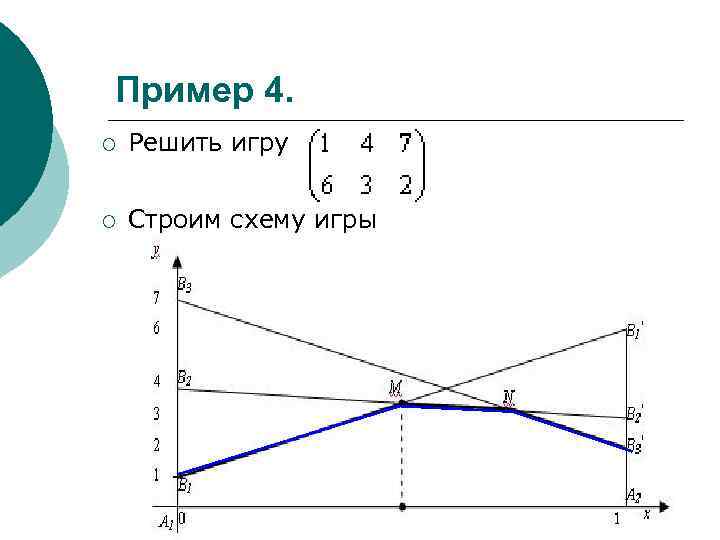Пример 4. ¡ Решить игру ¡ Строим схему игры

Пример 4. ¡ ¡ ¡ Выделяем нижнюю границу выигрыша В 1 МNВ 3′ и находим наивысшую точку М этой границы; ордината точки М равна цене игры ν. Определяем пару стратегий, пересекающихся в точке оптимума М. В этой точке пересекаются отрезки В 2 В 2′ и В 1 В 1′, соответствующие стратегиям В 1 и В 2 игрока B. Следовательно, стратегию В 3 ему применять невыгодно. Исключаем из матрицы третий столбец и решаем полученную игру 2 x 2

Пример 4. Ответ: SA 0=(1/2; 1/2); SB 0=(1/6; 5/6; 0); ν=7/2.

Сведение матричных игр к задачам линейного программирования

Игра в форме задачи линейного программирования Каждая конечная парная игра с нулевой суммой может быть представлена как задача линейного программирования ¡ и, наоборот, любая задача линейного программирования может быть представлена как игра. ¡ Любую задачу линейного программирования можно решить симплексным методом. ¡

Игра в форме ЗЛП Для первого игрока модель игры - выигрыш при ограничениях - выигрыш не меньше цены игры - вероятности использования стратегий

Преобразование модели игры ¡ Разделим каждое ограничение на ν: ¡ Обозначим Xi=xi/v. Если , то ¡

Игра в форме ЗЛП Для первого игрока Для второго игрока при ограничениях Взаимно двойственные задачи

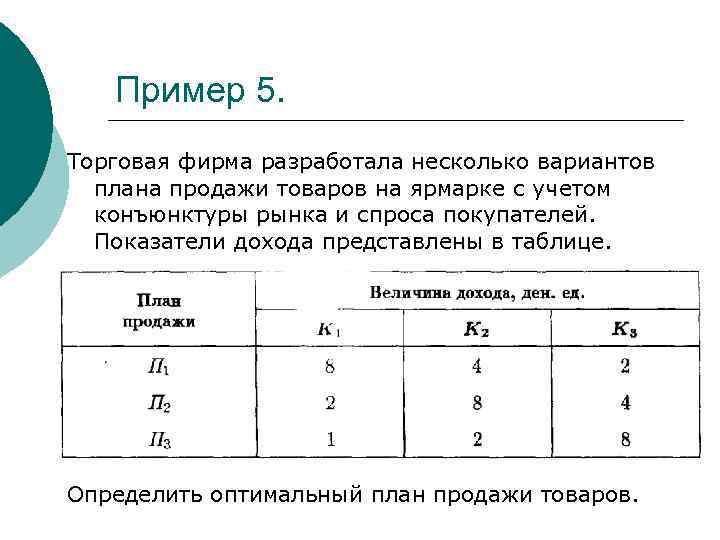Пример 5. Торговая фирма разработала несколько вариантов плана продажи товаров на ярмарке с учетом конъюнктуры рынка и спроса покупателей. Показатели дохода представлены в таблице. Определить оптимальный план продажи товаров.

Пример 5. ¡ Обозначим: l вероятность применения торговой фирмой стратегии П 1 — x 1, стратегии П 2 —x 2, П 3 — х3; l вероятность использования стратегии К 1 — у1, стратегии К 2 — y 2, К 3 — у3. Модель для первого игрока (торговой фирмы): при ограничениях Модель для второго игрока (коньюнктуры рынка): при ограничениях

Пример 5. ¡ Найдем оптимальное решение задачи для первого игрока симплексным методом*. Хопт = (5/49, 11/196, 1/14), L(X)min = 45/196 xi=Xi*v v =1/L(X)=196/45 ¡ Получим Ответ: фирма должна придерживаться стратегии при этом она получит доход не менее v =196/45≈4, 36 ден. ед.

Алгоритм решения игры 1. 2. 3. 4. Исключить из платежной матрицы заведомо невыгодные стратегии. Определить верхнюю и нижнюю границу игры, проверить наличие седловой точки. Если она есть, решить задачу в чистых стратегиях. Если седловая точка отсутствует, а игра имеет размерность 2×n или m× 2, решить ее графическим методом. При отсутствии седловой точки и большей размерности матрицы, свести игру к задаче линейного программирования.

Игры с «природой»

Игры с «природой» Основная особенность: информация об условиях осуществления действия (хода) отсутствует или неопределенна Игроки: Человек – игрок, действующий целенаправленно (обычно первый игрок) Природа – игрок, действующий случайно;

Принятие решений в условиях неопределенности Критерии выбора стратегии ¡ Вальде (пессимистический): max (min aij) ¡ максимума (оптимистический): max (max aij) ¡ Гурвица: max (α*min aij + (1 -α)*max aij)), α – степень оптимизма ¡ Сэвиджа: 1)строится матрица рисков R: rij=(max aij)–aij 2)критерий min (max rij)

Пример 6. ¡ ¡ Фирма "Фармацевт" производит медикаменты. Известно, что пик спроса на лекарственные препараты 1 -й группы приходится на летний период (сердечно-сосудистой группы, анальгетики), на препараты 2 -й группы — на осенний и весенний периоды (антиинфекционные, противокашлевые). Затраты на производство 1 ед. продукции за сентябрь-октябрь составили: по 1 -й группе — 20 р. ; по 2 -й группе— 15 р. при цене продажи 40 р. и 30 р. соответственно. Службой маркетинга установлено, что фирма может реализовать в условиях теплой погоды 3050 ед. продукции 1 -й группы и 1100 ед. продукции 2 -й группы; в условиях холодной погоды — 1525 ед. продукции 1 -й группы и 3690 ед. 2 -й группы. Определить стратегию фирмы в выпуске продукции, обеспечивающую максимальный доход от её реализации.

Пример 6. Фирма располагает двумя стратегиями: ¡ A 1 — в этом году будет теплая погода; ¡ A 2 — погода будет холодная. Рассматривая фирму и погоду в качестве двух игроков, получим платежную матрицу Цена игры лежит в диапазоне 16 500 р. ≤ v ≤ 77 500 р.

Пример 6. ¡ ¡ Обозначим: x 1 – вероятность применения фирмой стратегии А 1, x 2— стратегии А 2 , причем х1 = 1—х2. Решим игру графическим методом, получим Хопт = (0, 56; 0, 44), при этом цена игры v = 46 986 р. Оптимальный план производства лекарственных препаратов составит Ответ: фирме целесообразно производить в течение сентября и октября 2379 ед. препаратов 1 -й группы и 2239, 6 ед. препаратов 2 -й группы, тогда при любой погоде она получит доход не менее 46 986 р.

Пример 6. Если не представляется возможным использовать смешанную стратегию (договоры с другими организациями), для определения оптимальной стратегии фирмы используем критерии: ¡ Критерий Вальде: фирме целесообразно использовать стратегию A 1. ¡ Критерий максимума: целесообразно использовать стратегию А 2.

Пример 6. Критерий Гурвица: для определенности примем α=0, 4, тогда для стратегии фирмы А 1 ¡ для стратегии А 2 фирме целесообразно использовать стратегию А 2

Пример 6. Критерий Сэвиджа. Максимальный элемент в первом столбце — 77 500, во втором столбце — 85 850. Элементы матрицы рисков найдём по формуле ¡ Матрица рисков имеет вид целесообразно использовать стратегию A 1 или А 2