55609622901f395e48aea12047a26851.ppt
- Количество слайдов: 145

List, (dynamic) linked list Let’s first forget about ‘classes’, but only a dynamic list. We make lists with ‘classes’ afterwards.

A simple list Example: using a dynamic array * concept of a list, e. g. a list of integers n n n * Print out info Empty test Search an element Insertion (at head, at end, any position) Deletion … implemented by a static array (over-sized if necessary) int list[1000]; int size; n by a dynamic array int list[size]; int size; n by a linked list and more … n
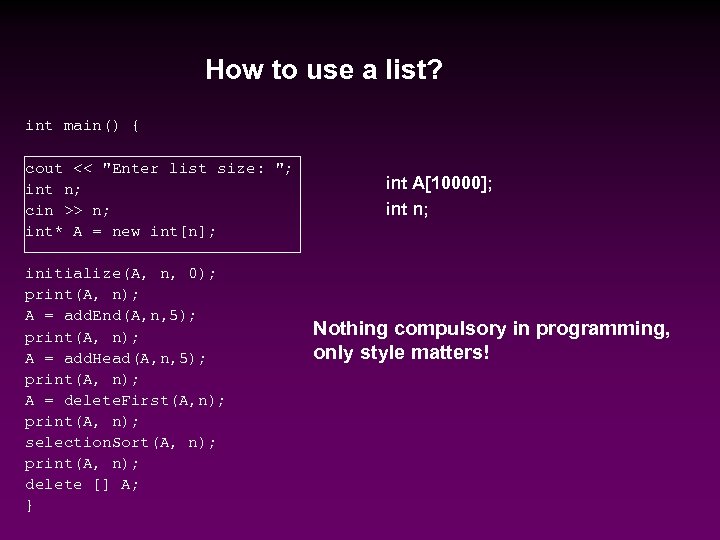
How to use a list? int main() { cout << "Enter list size: "; int n; cin >> n; int* A = new int[n]; initialize(A, n, 0); print(A, n); A = add. End(A, n, 5); print(A, n); A = add. Head(A, n, 5); print(A, n); A = delete. First(A, n); print(A, n); selection. Sort(A, n); print(A, n); delete [] A; } int A[10000]; int n; Nothing compulsory in programming, only style matters!
![Initialize void initialize(int list[], int size, int value){ for(int i=0; i<size; i++) list[i] = Initialize void initialize(int list[], int size, int value){ for(int i=0; i<size; i++) list[i] =](https://present5.com/presentation/55609622901f395e48aea12047a26851/image-4.jpg)
Initialize void initialize(int list[], int size, int value){ for(int i=0; i<size; i++) list[i] = value; }
![Print out a list void print(int list[], int size) { cout << "[ "; Print out a list void print(int list[], int size) { cout << "[ ";](https://present5.com/presentation/55609622901f395e48aea12047a26851/image-5.jpg)
Print out a list void print(int list[], int size) { cout << "[ "; for(int i=0; i<size; i++) cout << list[i] << " "; cout << "]" << endl; }

Delete the first element // for deleting the first element of the array int* delete. First(int list[], int& size){ int* new. List; new. List = new int[size-1]; // make new array if(size){ // copy and delete old array for(int i=0; i<size-1; i++) new. List[i] = list[i+1]; delete [] list; } size--; return new. List; }

Remark: Instead of A = delete. First(A, n) we can also just delete. First(A, n) if we define as a void type function: void delete. First(int*& A, int& size) { … A = new. List; } We can also B = delete. First(A, n) if we keep the original intact

Adding Elements // for adding a new element to end of array int* add. End(int list[], int& size, int value){ int* new. List; new. List = new int [size+1]; // make new array if(size){ // copy and delete old array for(int i=0; i<size; i++) new. List[i] = list[i]; delete [] list; } new. List[size] = value; size++; return new. List; }

Add at the beginning: // for adding a new element at the beginning of the array int* add. Head(int list[], int& size, int value){ int* new. List; new. List = new int [size+1]; // make new array if(size){ // copy and delete old array for(int i=0; i<size; i++) new. List[i+1] = list[i]; delete [] list; } new. List[0] = value; size++; return new. List; }

Linked list: a dynamic list
![Motivation * list using static array int my. Array[1000]; int n; We have to Motivation * list using static array int my. Array[1000]; int n; We have to](https://present5.com/presentation/55609622901f395e48aea12047a26851/image-11.jpg)
Motivation * list using static array int my. Array[1000]; int n; We have to decide (to oversize) in advance the size of the array (list) * list using dynamic array int* my. Array; int n; cin >> n; my. Array = new int[n]; We allocate an array (list) of any specified size while the program is running * linked-list (dynamic size) size = ? ? The list is dynamic. It can grow and shrink to any size.
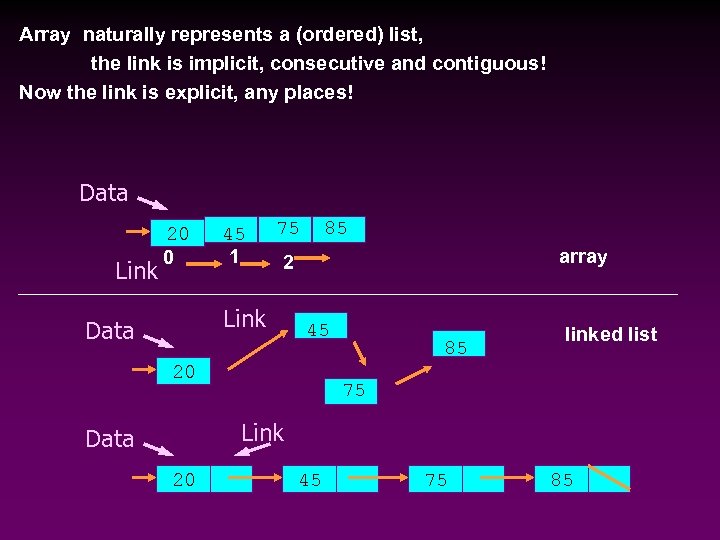
Array naturally represents a (ordered) list, the link is implicit, consecutive and contiguous! Now the link is explicit, any places! Data Link 20 0 45 1 75 array 2 Link Data 85 45 20 85 linked list 75 Link Data 20 45 75 85

Linked Lists: Basic Idea * * A linked list is an ordered collection of data Each element of the linked list has Some data n A link to the next element n * The link is used to chain the data Example: A linked list of integers: Link Data 20 45 75 85

Linked Lists: Basic Ideas * The list can grow and shrink 20 45 add. End(75), add. End(85) 20 45 75 85 delete. End(85), delete. Head(20), delete. Head(45) 75
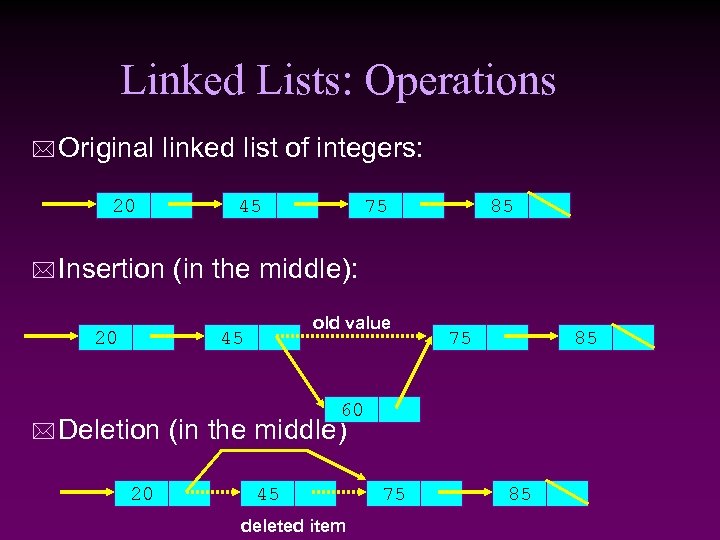
Linked Lists: Operations * Original linked list of integers: 20 45 75 85 * Insertion (in the middle): 20 old value 45 75 85 60 * Deletion (in the middle) 20 45 deleted item 75 85

Definition of linked list type: struct Node{ int data; Node* next; }; We can also: typedef Node* Node. Ptr;

Linked List Structure * Node : Data + Link n Definition struct Node { int data; Node* next; }; n Create a Node* p; p = new Node; n //contains useful information //points to next element or NULL Delete a Node delete p; //points to newly allocated memory

n Access fields in a node (*p). data; //access the data field (*p). next; //access the pointer field Or it can be accessed this way p->data //access the data field p->next //access the pointer field
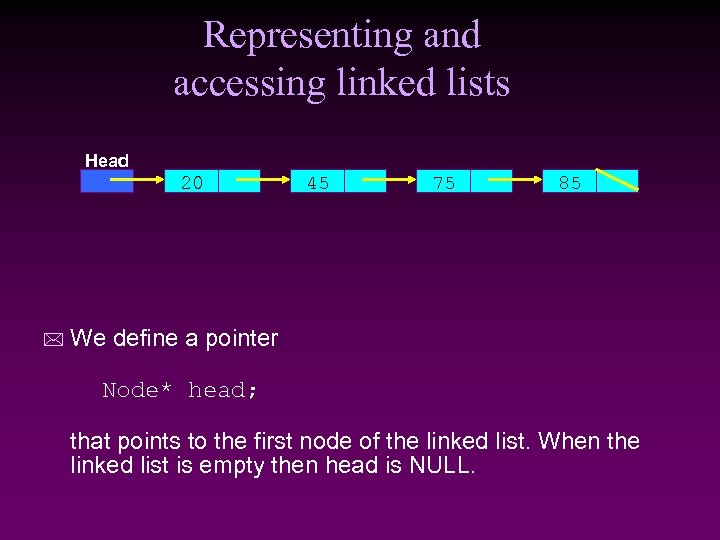
Representing and accessing linked lists Head 20 * 45 75 85 We define a pointer Node* head; that points to the first node of the linked list. When the linked list is empty then head is NULL.

Passing a Linked List to a Function It is roughly the same as for an array!!! * When passing a linked list to a function it should suffice to pass the value of head. Using the value of head the function can access the entire list. * Problem: If a function changes the beginning of a list by inserting or deleting a node, then head will no longer point to the beginning of the list. Solution: When passing head always pass it by reference (not good!) or using a function to return a new pointer value *

Implementation of an (Unsorted) Linked List
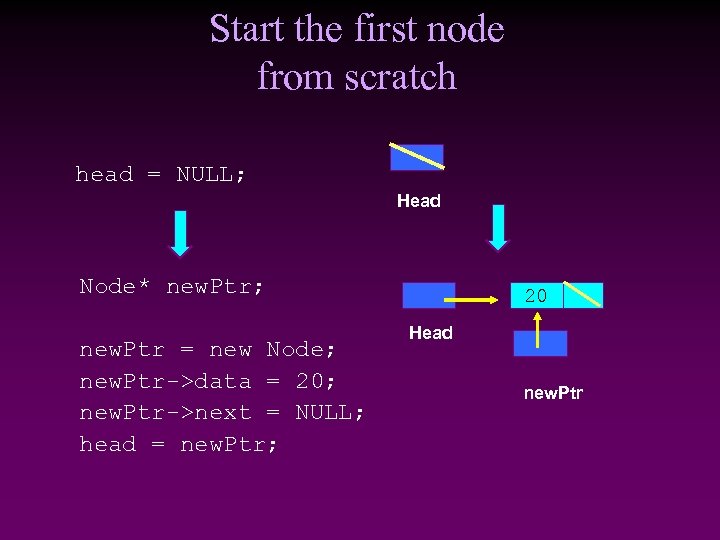
Start the first node from scratch head = NULL; Head Node* new. Ptr; new. Ptr = new Node; new. Ptr->data = 20; new. Ptr->next = NULL; head = new. Ptr; 20 Head new. Ptr
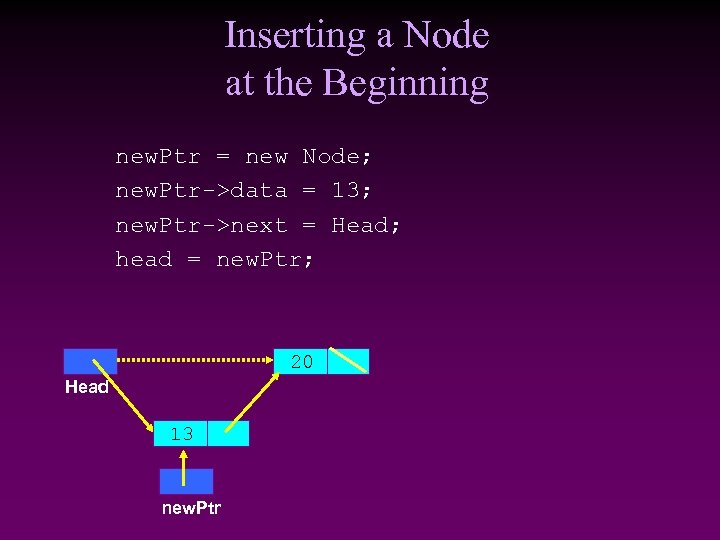
Inserting a Node at the Beginning new. Ptr = new Node; new. Ptr->data = 13; new. Ptr->next = Head; head = new. Ptr; 20 Head 13 new. Ptr

Keep going … Head 50 new. Ptr 40 13 20

Adding an element to the head: Node. Ptr& void add. Head(Node*& head, int newdata){ Node* new. Ptr = new Node; new. Ptr->data = newdata; new. Ptr->next = Head; head = new. Ptr; } Call by reference, scaring!!!

Also written (more functionally) as: Node* add. Head(Node* head, int newdata){ Node* new. Ptr = new Node; new. Ptr->data = newdata; new. Ptr->next = Head; return new. Ptr; } Compare it with ‘add. Head’ with a dynamic array implementation

Deleting the Head Node* p; p = head; head = head->next; delete p; head (to delete) 50 p 40 13 20
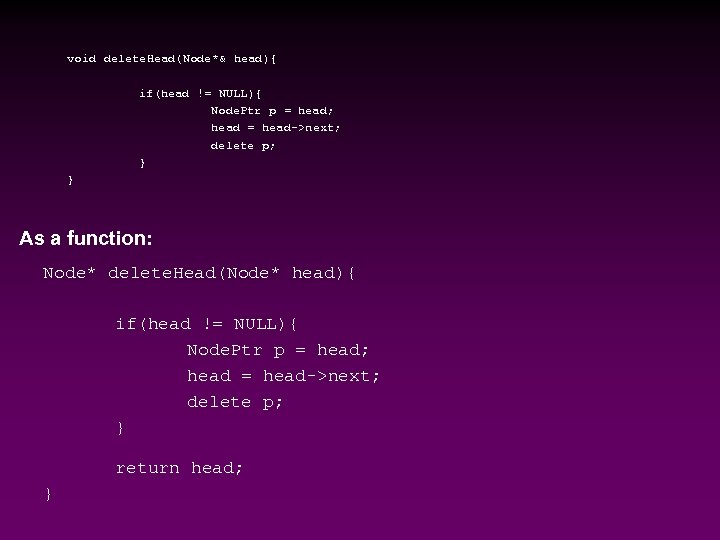
void delete. Head(Node*& head){ if(head != NULL){ Node. Ptr p = head; head = head->next; delete p; } } As a function: Node* delete. Head(Node* head){ if(head != NULL){ Node. Ptr p = head; head = head->next; delete p; } return head; }
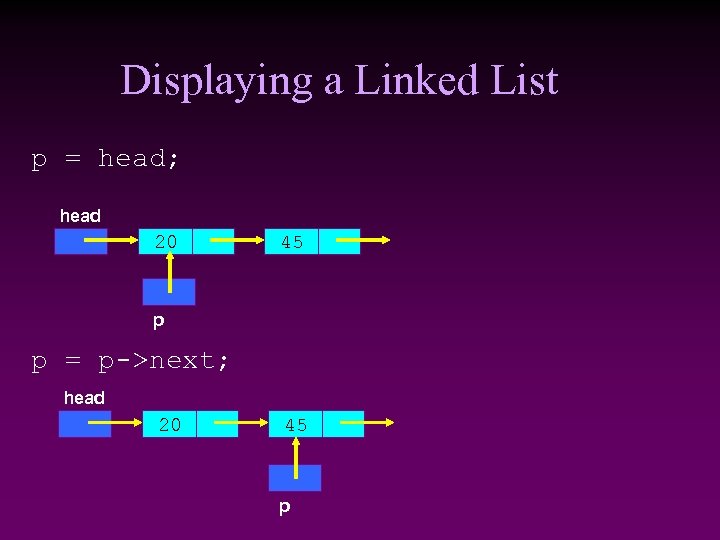
Displaying a Linked List p = head; head 20 45 p p = p->next; head 20 45 p

A linked list is displayed by walking through its nodes one by one, and displaying their data fields (similar to an array!). void display. List(Node* head){ Node. Ptr p; p = head; while(p != NULL){ cout << p->data << endl; p = p->next; } } For an array: void display. Array(int data[], int size) int n=0; while ( n<size ) { cout << data[i] << endl; n++; } } {
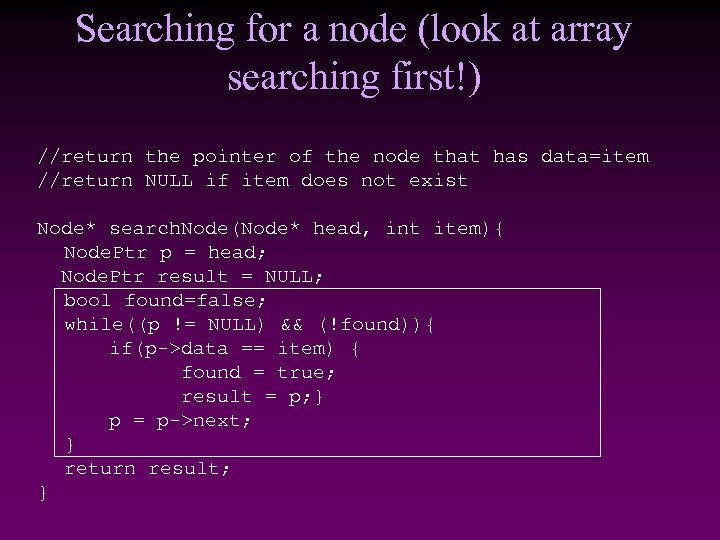
Searching for a node (look at array searching first!) //return the pointer of the node that has data=item //return NULL if item does not exist Node* search. Node(Node* head, int item){ Node. Ptr p = head; Node. Ptr result = NULL; bool found=false; while((p != NULL) && (!found)){ if(p->data == item) { found = true; result = p; } p = p->next; } return result; }
![Remember array searching algorithm: void main() { const int size=8; int data[size] = { Remember array searching algorithm: void main() { const int size=8; int data[size] = {](https://present5.com/presentation/55609622901f395e48aea12047a26851/image-32.jpg)
Remember array searching algorithm: void main() { const int size=8; int data[size] = { 10, 7, 9, 1, 17, 30, 5, 6 }; int value; cout << "Enter search element: "; cin >> value; int n=0; int position=-1; bool found=false; while ( (n<size) && (!found) ) { if(data[n] == value) { found=true; position=n; } n++; } if(position==-1) cout << "Not found!!n"; else cout << "Found at: " << position << endl; } It is essentially the same!

Variations of linked lists * Unsorted linked lists * Sorted linked lists * Circular linked lists * Doubly linked lists *…

Further considerations for the unsorted lists: * Physical copy of list for operators like ‘delete. Head’ and ‘add. Head’ * ‘delete. Head’ should be understood as a decomposition into a sub-list …
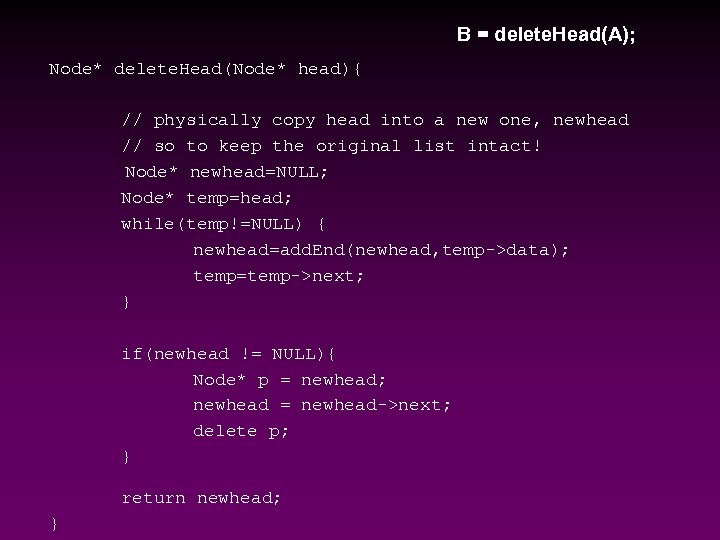
B = delete. Head(A); Node* delete. Head(Node* head){ // physically copy head into a new one, newhead // so to keep the original list intact! Node* newhead=NULL; Node* temp=head; while(temp!=NULL) { newhead=add. End(newhead, temp->data); temp=temp->next; } if(newhead != NULL){ Node* p = newhead; newhead = newhead->next; delete p; } return newhead; }

More operation: adding to the end * Original linked list of integers: 50 * 40 13 20 Add to the end (insert at the end): 50 40 13 20 60 Last element The key is how to locate the last element or node of the list!
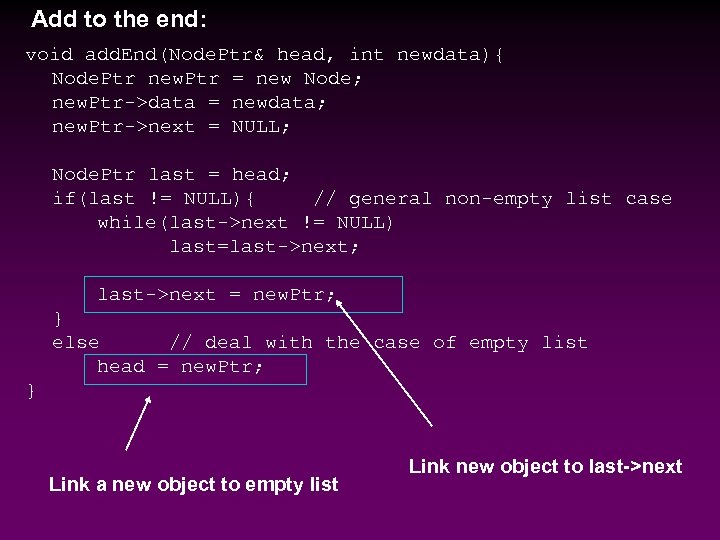
Add to the end: void add. End(Node. Ptr& head, int newdata){ Node. Ptr new. Ptr = new Node; new. Ptr->data = newdata; new. Ptr->next = NULL; Node. Ptr last = head; if(last != NULL){ // general non-empty list case while(last->next != NULL) last=last->next; last->next = new. Ptr; } else // deal with the case of empty list head = new. Ptr; } Link a new object to empty list Link new object to last->next

Add to the end as a function: Node. Ptr add. End(Node. Ptr head, int newdata){ Node. Ptr new. Ptr = new Node; new. Ptr->data = newdata; new. Ptr->next = NULL; Node. Ptr last = head; if(last != NULL){ // general non-empty list case while(last->next != NULL) last=last->next; last->next = new. Ptr; } else // deal with the case of empty list head = new. Ptr; return head; }

Implementation of a Sorted Linked List
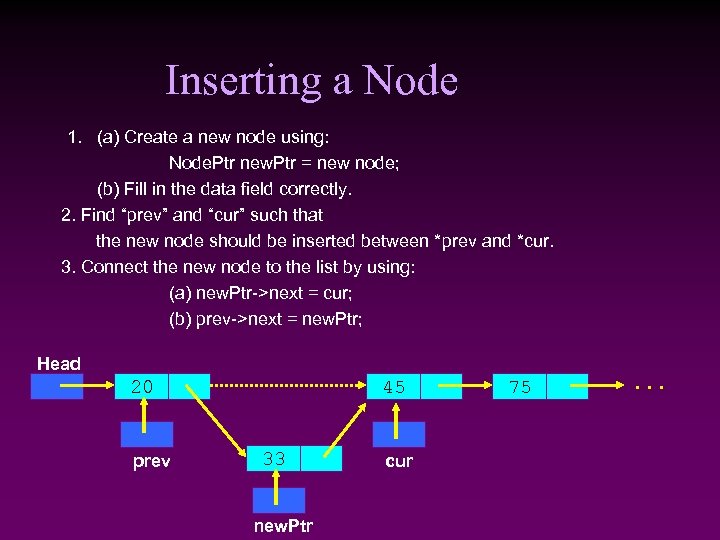
Inserting a Node 1. (a) Create a new node using: Node. Ptr new. Ptr = new node; (b) Fill in the data field correctly. 2. Find “prev” and “cur” such that the new node should be inserted between *prev and *cur. 3. Connect the new node to the list by using: (a) new. Ptr->next = cur; (b) prev->next = new. Ptr; Head 20 prev 45 33 new. Ptr cur 75 . . .

Finding prev and cur Suppose that we want to insert or delete a node with data value new. Value. Then the following code successfully finds prev and cur such that prev->data < new. Value <= cur->data

It’s a kind of search algo, prev = NULL; cur = head; found=false; while( (cur!=NULL) && (!found) ) { if (new. Value > cur->data) { prev=cur; cur=cur->next; } else found = true; } Prev is necessary as we can’t go back!

Finally, it is equivalent to: prev = NULL; cur = head; while( (cur!=NULL) && (new. Value>cur->data) ) { prev=cur; cur=cur->next; } Logical AND (&&) is short-circuited, sequential, i. e. if the first part is false, the second part will not be executed.
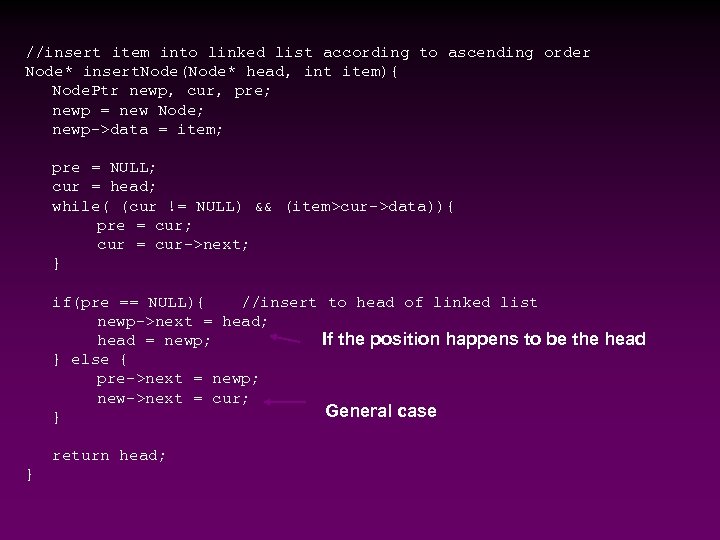
//insert item into linked list according to ascending order Node* insert. Node(Node* head, int item){ Node. Ptr newp, cur, pre; newp = new Node; newp->data = item; pre = NULL; cur = head; while( (cur != NULL) && (item>cur->data)){ pre = cur; cur = cur->next; } if(pre == NULL){ //insert to head of linked list newp->next = head; head = newp; If the position happens to be the head } else { pre->next = newp; new->next = cur; General case } return head; }
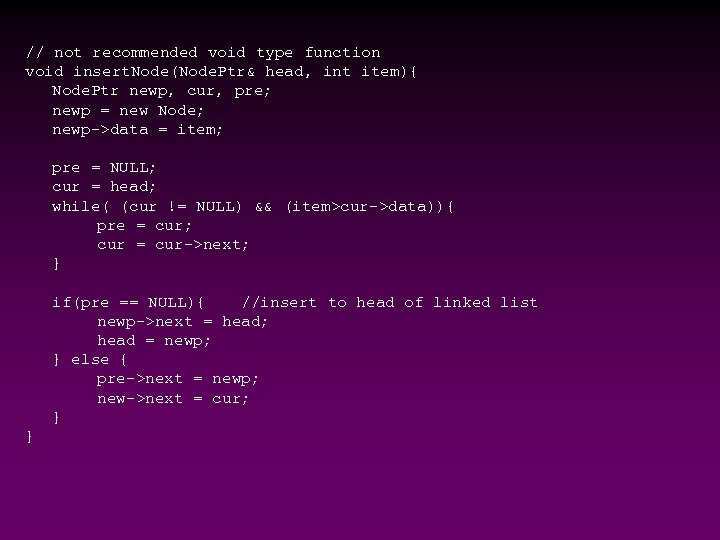
// not recommended void type function void insert. Node(Node. Ptr& head, int item){ Node. Ptr newp, cur, pre; newp = new Node; newp->data = item; pre = NULL; cur = head; while( (cur != NULL) && (item>cur->data)){ pre = cur; cur = cur->next; } if(pre == NULL){ //insert to head of linked list newp->next = head; head = newp; } else { pre->next = newp; new->next = cur; } }
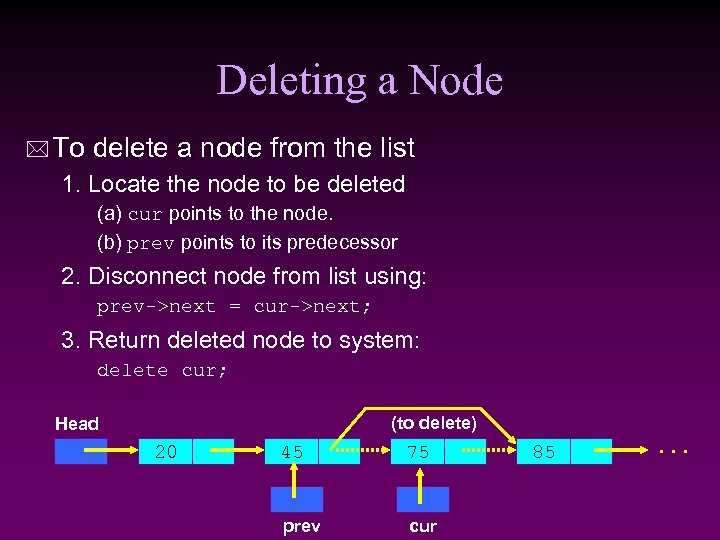
Deleting a Node * To delete a node from the list 1. Locate the node to be deleted (a) cur points to the node. (b) prev points to its predecessor 2. Disconnect node from list using: prev->next = cur->next; 3. Return deleted node to system: delete cur; (to delete) Head 20 45 75 prev cur 85 . . .
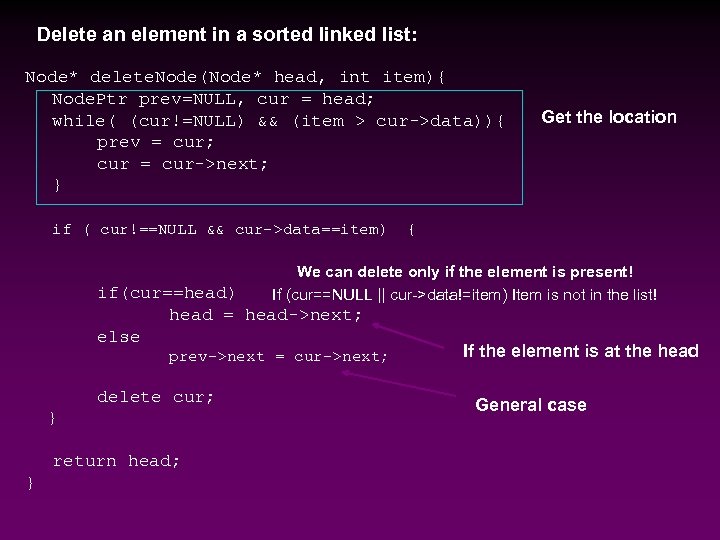
Delete an element in a sorted linked list: Node* delete. Node(Node* head, int item){ Node. Ptr prev=NULL, cur = head; while( (cur!=NULL) && (item > cur->data)){ prev = cur; cur = cur->next; } if ( cur!==NULL && cur->data==item) Get the location { We can delete only if the element is present! If (cur==NULL || cur->data!=item) Item is not in the list! if(cur==head) head = head->next; else prev->next = cur->next; delete cur; } return head; } If the element is at the head General case

// in a void function, not recommended void delete. Node(Node. Ptr& head, int item){ Node. Ptr prev=NULL, cur = head; while( (cur!=NULL) && (item > cur->data)){ prev = cur; cur = cur->next; } if ( cur!==NULL && cur->data==item) Get the location { We can delete only if the element is present! If (cur==NULL || cur->data!=item) Item is not in the list! if(cur==Head) Head = Head->next; else If the element is at the head prev->next = cur->next; delete cur; } } General case

Example of a (dynamic) class: linked list class
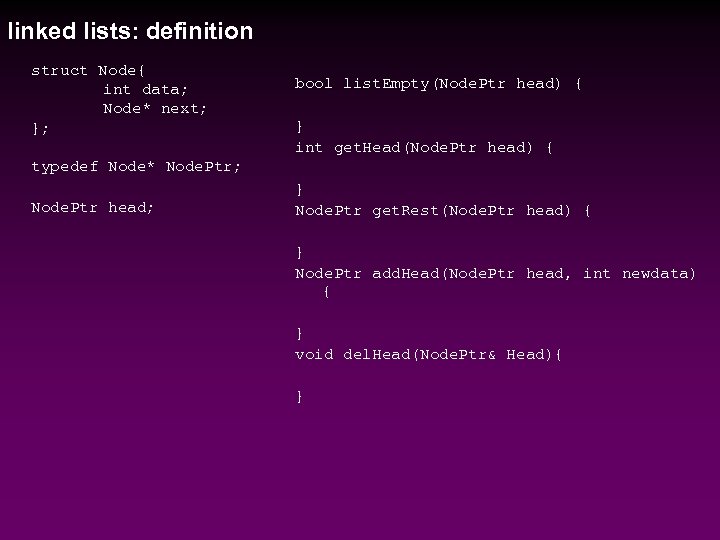
linked lists: definition struct Node{ int data; Node* next; }; bool list. Empty(Node. Ptr head) { } int get. Head(Node. Ptr head) { typedef Node* Node. Ptr; Node. Ptr head; } Node. Ptr get. Rest(Node. Ptr head) { } Node. Ptr add. Head(Node. Ptr head, int newdata) { } void del. Head(Node. Ptr& Head){ }
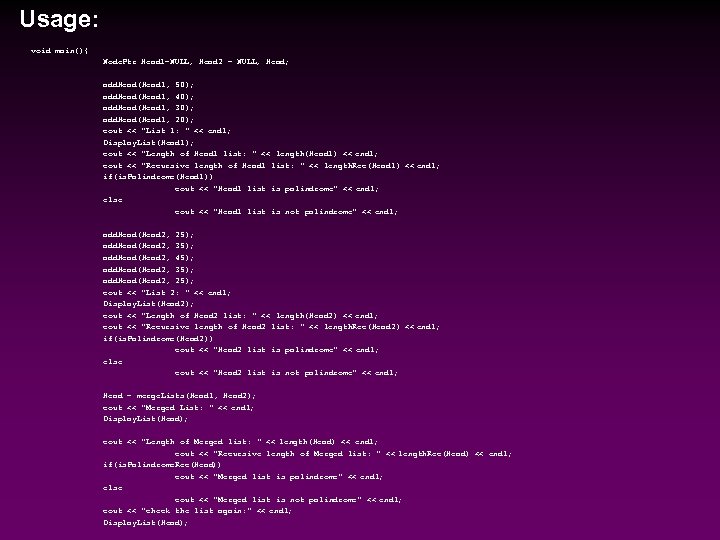
Usage: void main(){ Node. Ptr Head 1=NULL, Head 2 = NULL, Head; add. Head(Head 1, 50); add. Head(Head 1, 40); add. Head(Head 1, 30); add. Head(Head 1, 20); cout << "List 1: " << endl; Display. List(Head 1); cout << "Length of Head 1 list: " << length(Head 1) << endl; cout << "Recursive length of Head 1 list: " << length. Rec(Head 1) << endl; if(is. Palindrome(Head 1)) cout << "Head 1 list is palindrome" << endl; else cout << "Head 1 list is not palindrome" << endl; add. Head(Head 2, 25); add. Head(Head 2, 35); add. Head(Head 2, 45); add. Head(Head 2, 35); add. Head(Head 2, 25); cout << "List 2: " << endl; Display. List(Head 2); cout << "Length of Head 2 list: " << length(Head 2) << endl; cout << "Recursive length of Head 2 list: " << length. Rec(Head 2) << endl; if(is. Palindrome(Head 2)) cout << "Head 2 list is palindrome" << endl; else cout << "Head 2 list is not palindrome" << endl; Head = merge. Lists(Head 1, Head 2); cout << "Merged List: " << endl; Display. List(Head); cout << "Length of Merged list: " << length(Head) << endl; cout << "Recursive length of Merged list: " << length. Rec(Head) << endl; if(is. Palindrome. Rec(Head)) cout << "Merged list is palindrome" << endl; else cout << "Merged list is not palindrome" << endl; cout << "check the list again: " << endl; Display. List(Head);

Make an Abstract Data Type l l One more example of ADT: l integer linked list using class A class with dynamic objects: l Copy constructor l Destructor

struct Node{ public: int data; Node* next; }; typedef Node* Nodeptr; ‘new’ member functions class list { public: list(); // constructor list(const list& list 1); // copy constructor ~list(); // destructor bool empty() const; int head. Element() const; // boolean function // access functions void add. Head(int newdata); void delete. Head(); // add to the head // delete the head int length() const; void print() const; private: Nodeptr head; }; // utility function // output ‘old’ operations
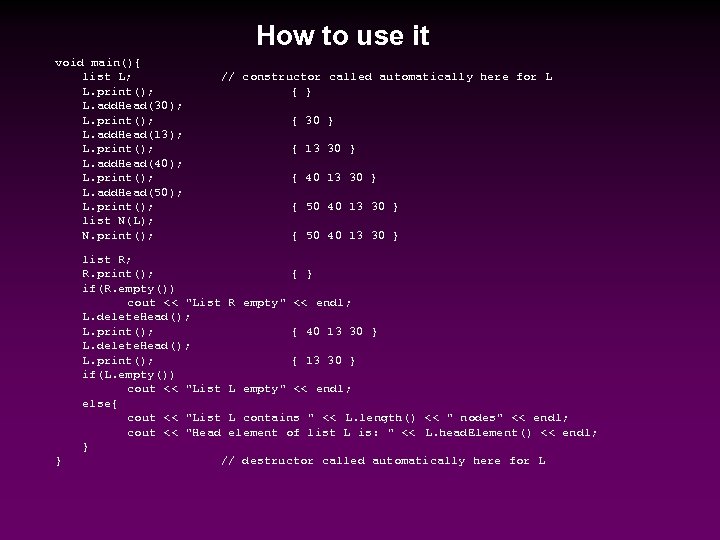
How to use it void main(){ list L; L. print(); L. add. Head(30); L. print(); L. add. Head(13); L. print(); L. add. Head(40); L. print(); L. add. Head(50); L. print(); list N(L); N. print(); } // constructor called automatically here for L { } { 30 } { 13 30 } { 40 13 30 } { 50 40 13 30 } list R; R. print(); { } if(R. empty()) cout << "List R empty" << endl; L. delete. Head(); L. print(); { 40 13 30 } L. delete. Head(); L. print(); { 13 30 } if(L. empty()) cout << "List L empty" << endl; else{ cout << "List L contains " << L. length() << " nodes" << endl; cout << "Head element of list L is: " << L. head. Element() << endl; } // destructor called automatically here for L

Implementation Some simple member functions: list: : list(){ head = NULL; } bool list: : empty() const{ if(head==NULL) return true; else return false; } int list: : head. Element() const { if(head != NULL) return head->data; else{ cout << "error: trying to find head of empty list" << endl; exit(1); } }
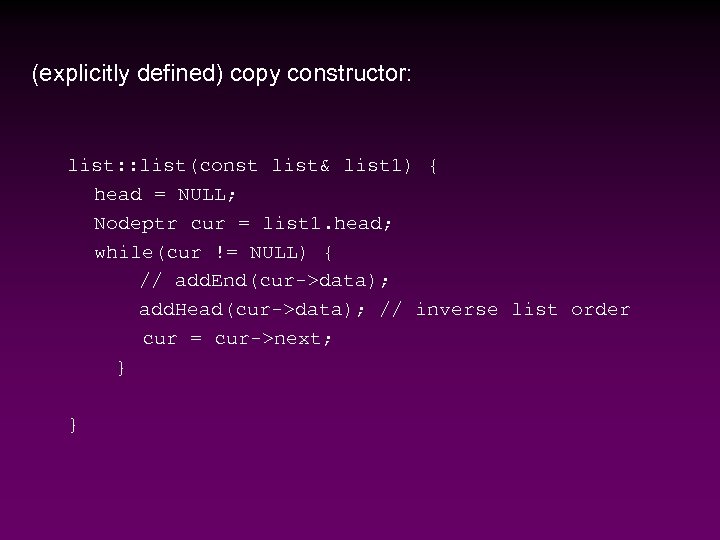
(explicitly defined) copy constructor: list: : list(const list& list 1) { head = NULL; Nodeptr cur = list 1. head; while(cur != NULL) { // add. End(cur->data); add. Head(cur->data); // inverse list order cur = cur->next; } }

Destructor: deallocation function list: : ~list(){ Nodeptr cur; while(head!=NULL){ cur = head; head = head->next; delete cur; } }

Adding an element to the head: void list: : add. Head(int newdata){ Nodeptr new. Ptr = new Node; new. Ptr->data = newdata; new. Ptr->next = head; head = new. Ptr; }
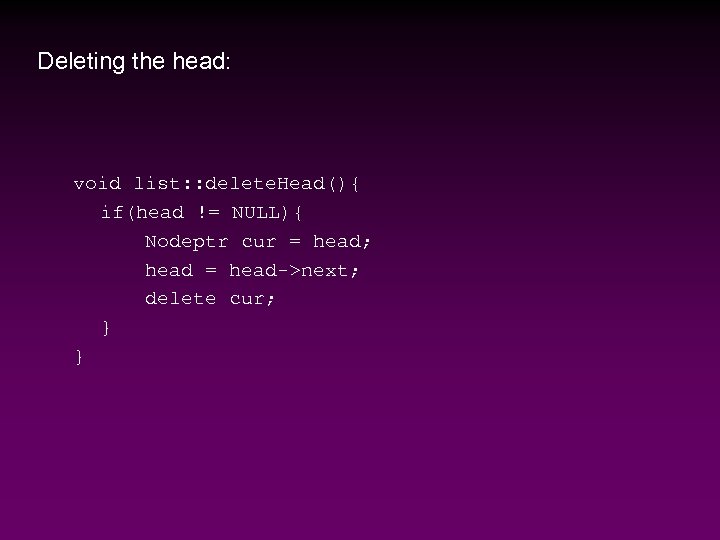
Deleting the head: void list: : delete. Head(){ if(head != NULL){ Nodeptr cur = head; head = head->next; delete cur; } }
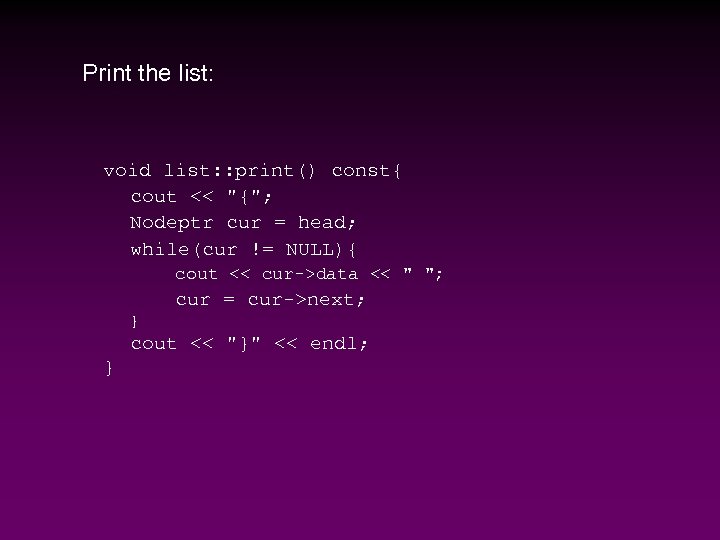
Print the list: void list: : print() const{ cout << "{"; Nodeptr cur = head; while(cur != NULL){ cout << cur->data << " "; cur = cur->next; } cout << "}" << endl; }
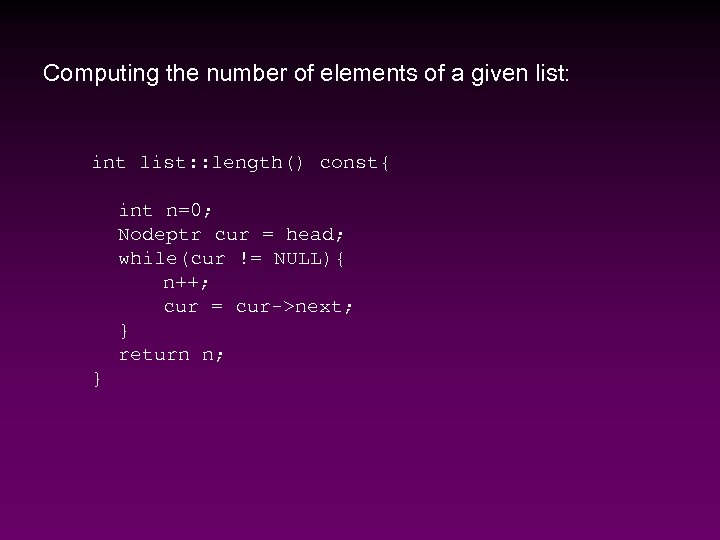
Computing the number of elements of a given list: int list: : length() const{ int n=0; Nodeptr cur = head; while(cur != NULL){ n++; cur = cur->next; } return n; }
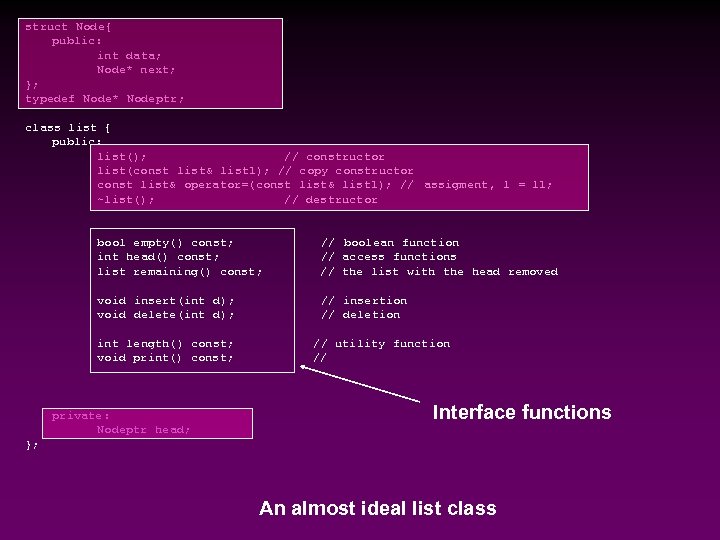
struct Node{ public: int data; Node* next; }; typedef Node* Nodeptr; class list { public: list(); // constructor list(const list& list 1); // copy constructor const list& operator=(const list& list 1); // assigment, l = l 1; ~list(); // destructor bool empty() const; int head() const; list remaining() const; // boolean function // access functions // the list with the head removed void insert(int d); void delete(int d); // insertion // deletion int length() const; void print() const; private: Nodeptr head; // utility function // Interface functions }; An almost ideal list class

copy constructor: list: : list(const list. Class& list 1) { head = NULL; Nodeptr cur = list 1. head; while(cur != NULL) { // add. End(cur->data); add. Head(cur->data); // inverse list order cur = cur->next; } Operator assignment, ‘deep copy’ } Const list& operator=(const list& list 1) { if (this != &list 1) { head = NULL; Nodeptr cur = list 1. head; while(cur != NULL) { // add. End(cur->data); add. Head(cur->data); // inverse list order cur = cur->next; } return *this; } Delete[] head; Big three: copy constructor, operator=, destructor

Usage difference list l 1, l 2; node* head 1, head 2; head 1 = NULL; head 2 = NULL l 1. add. End(5); add. End(head 1, 5); list l 3(l 1); node* head 3 = NULL; l 3 = l 2; copylist(head 1, head 3); head 3 = head 2;

Doubly Linked List

Motivation * Doubly linked lists are useful for playing video and sound files with “rewind” and instant “replay” * They are also useful for other linked data where “require” a “fast forward” of the data as needed

* list using an array: Knowledge of list size n Access is easy (get the ith element) n Insertion/Deletion is harder n * list using ‘singly’ linked lists: Insertion/Deletion is easy n Access is harder n n But, can not ‘go back’!

Doubly Linked Lists In a Doubly Linked-List each item points to both its predecessor and successor prev points to the predecessor n next points to the successor n 10 Head 20 Cur->prev 40 Cur 55 Cur->next 70

Doubly Linked List Definition struct Node{ int data; Node* next; Node* prev; }; typedef Node* Node. Ptr;

Doubly Linked List Operations * insert. Node(Node. Ptr& Head, int item) //add new node to ordered doubly linked //list * delete. Node(Node. Ptr& Head, int item) //remove a node from doubly linked list * Search. Node(Node. Ptr Head, int item) * Print(node. Ptr Head, int item)
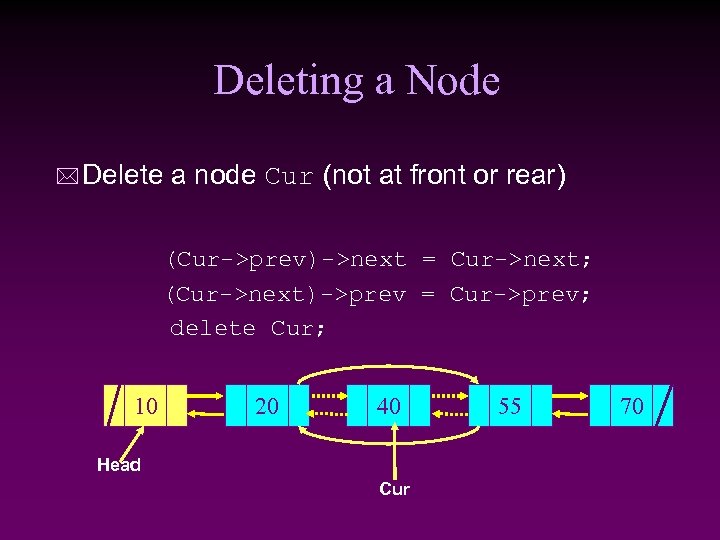
Deleting a Node * Delete a node Cur (not at front or rear) (Cur->prev)->next = Cur->next; (Cur->next)->prev = Cur->prev; delete Cur; 10 20 40 Head Cur 55 70

void delete. Node(Node. Ptr& head, int item) { Node. Ptr cur; cur = search. Node(head, item); if (head==NULL) { … } else if (cur->prev == NULL) { … } else if (cur->next==NULL) { … } else { Empty case At-the-beginning case At-the-end case General case (cur->prev)->next = cur->next; (cur->next)->prev = cur->prev; delete cur; } } A systematic way is to start from all these cases, then try to simply the codes, …
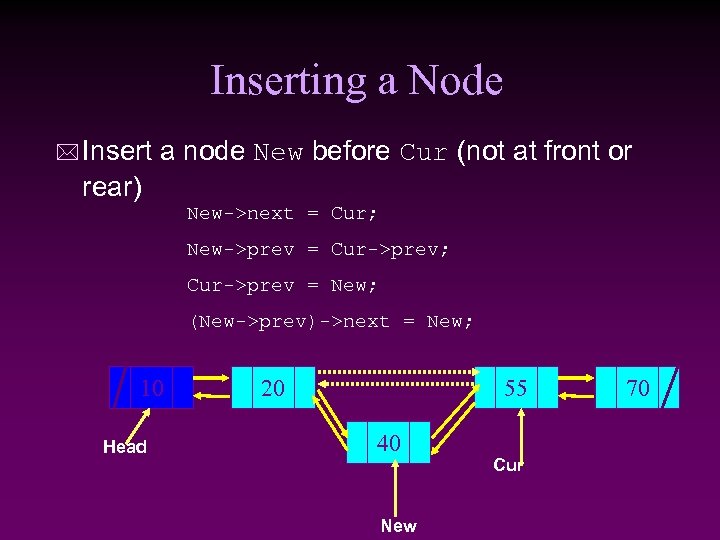
Inserting a Node * Insert a node New before Cur (not at front or rear) New->next = Cur; New->prev = Cur->prev; Cur->prev = New; (New->prev)->next = New; 10 Head 20 55 40 New Cur 70
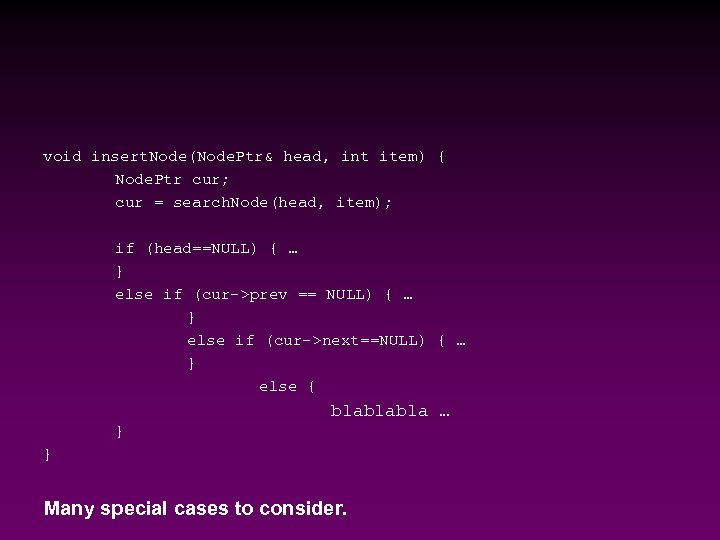
void insert. Node(Node. Ptr& head, int item) { Node. Ptr cur; cur = search. Node(head, item); if (head==NULL) { … } else if (cur->prev == NULL) { … } else if (cur->next==NULL) { … } else { blablabla … } } Many special cases to consider.

Many different linked lists … * singly linked lists Without ‘dummy’ n With dummy n circular n * doubly linked lists Without ‘dummy’ n With dummy n Using ‘dummy’ is a matter of personal preference! + simplify codes (not that much - Less logically sounds
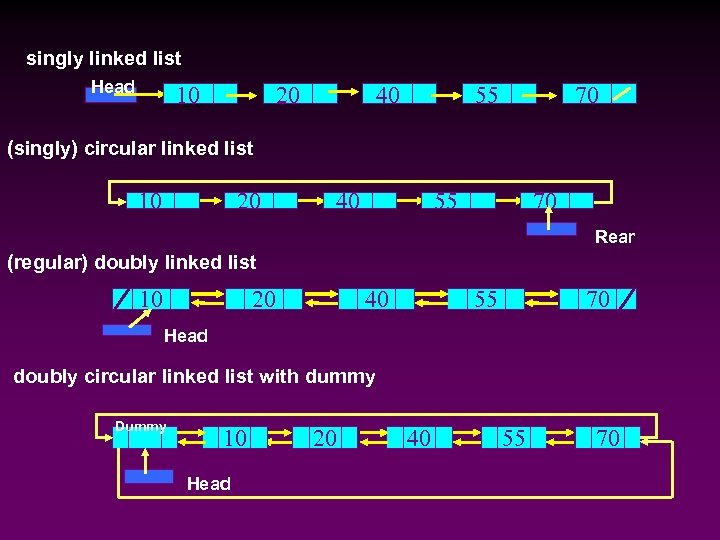
singly linked list Head 10 20 20 40 55 70 (singly) circular linked list 10 20 40 55 70 Rear (regular) doubly linked list 10 20 40 55 70 Head doubly circular linked list with dummy Dummy 10 Head 20 40 55 70

Doubly Linked Lists with Dummy Head Node * To simplify insertion and deletion by avoiding special cases of deletion and insertion at front and rear, a dummy head node is added at the head of the list * The last node also points to the dummy head node as its successor

Idea of ‘dummy’ object ‘dummy object’ is also called a ‘sentinel’, it allows the simplification of special cases, but confuses the emptyness NULL! l l Instead of pointing to NULL, point to the ‘dummy’!!! Skip over the dummy for the real list Dummy Head Node 10 Head 20 40 55 70
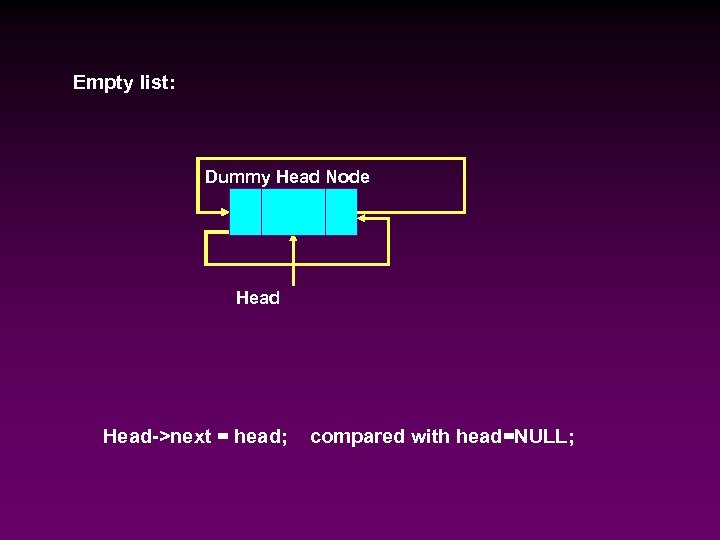
Empty list: Dummy Head Node Head->next = head; compared with head=NULL;

operations creation Doubly linked with dummy void create. Head(Node. Ptr& head){ head = new Node; head->next = head; head->prev = head; } Singly linked Node. Ptr head=NULL; Node. Ptr head; create. Head(head); reference Node. Ptr cur=head; Start from cur=cur->next; cur=head; Empty test cur=head; // dummy head cur=NULL; // or head=NULL;
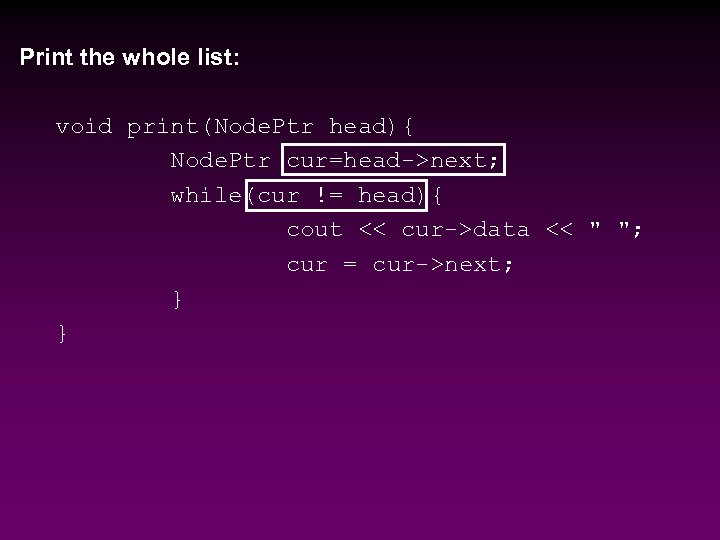
Print the whole list: void print(Node. Ptr head){ Node. Ptr cur=head->next; while(cur != head){ cout << cur->data << " "; cur = cur->next; } }

Searching a node (returning NULL if not found the element): Node. Ptr search. Node(Node. Ptr head, int item){ Node. Ptr cur = head->next; while ((cur != head) && (item != cur->data)) cur=cur->next; if (cur == head) cur = NULL; // we didn’t find return cur; } End of the list, empty
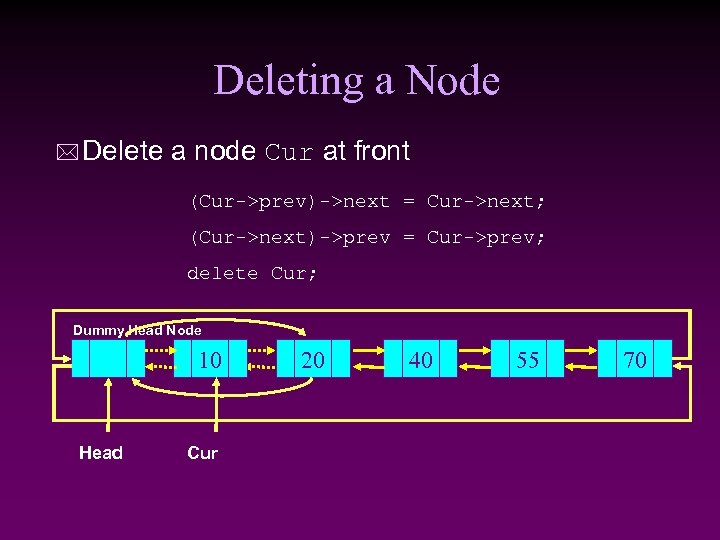
Deleting a Node * Delete a node Cur at front (Cur->prev)->next = Cur->next; (Cur->next)->prev = Cur->prev; delete Cur; Dummy Head Node 10 Head Cur 20 40 55 70

* Delete a node Cur in the middle (Cur->prev)->next = Cur->next; (Cur->next)->prev = Cur->prev; delete Cur; // same as delete front! Dummy Head Node 10 Head 20 40 Cur 55 70

* Delete a node Cur at rear (Cur->prev)->next = Cur->next; (Cur->next)->prev = Cur->prev; delete Cur; // same as delete front and middle! Dummy Head Node 10 Head 20 40 55 70 Cur
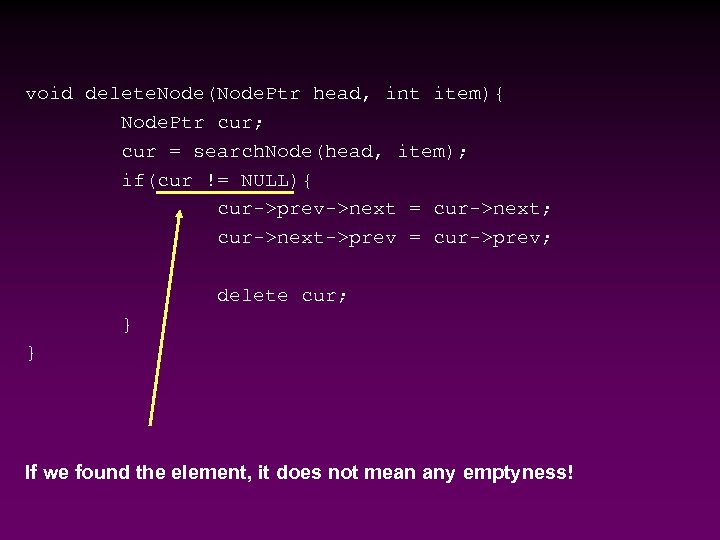
void delete. Node(Node. Ptr head, int item){ Node. Ptr cur; cur = search. Node(head, item); if(cur != NULL){ cur->prev->next = cur->next; cur->next->prev = cur->prev; delete cur; } } If we found the element, it does not mean any emptyness!
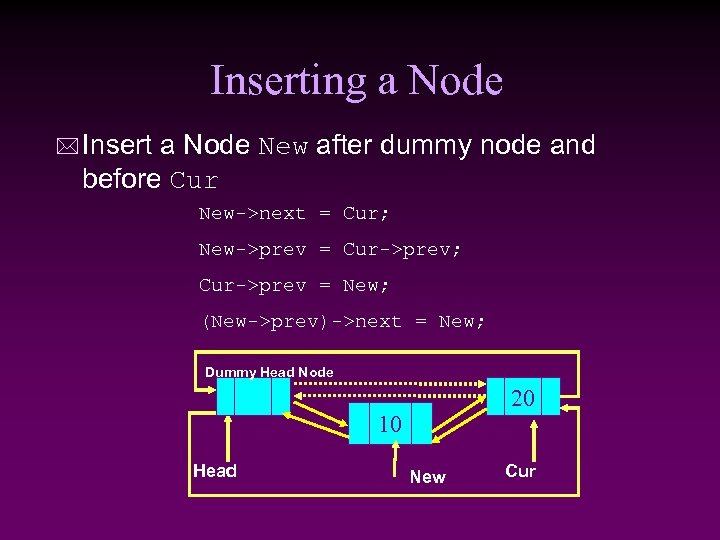
Inserting a Node * Insert a Node New after dummy node and before Cur New->next = Cur; New->prev = Cur->prev; Cur->prev = New; (New->prev)->next = New; Dummy Head Node 20 10 Head New Cur
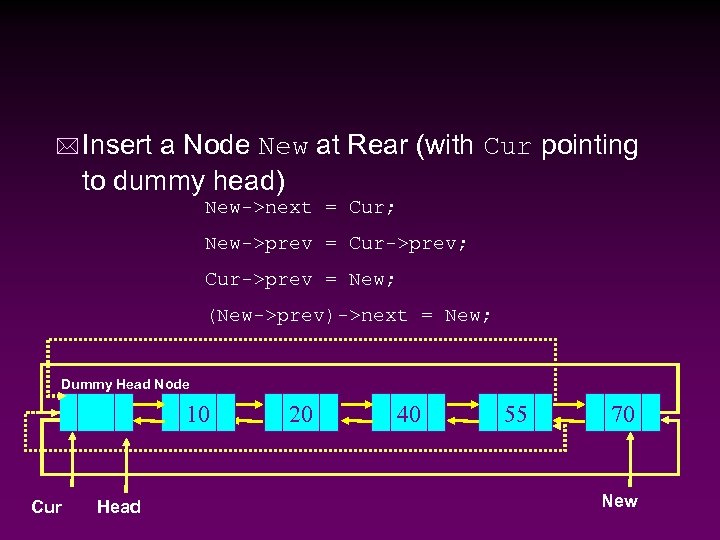
* Insert a Node New at Rear (with Cur pointing to dummy head) New->next = Cur; New->prev = Cur->prev; Cur->prev = New; (New->prev)->next = New; Dummy Head Node 10 Cur Head 20 40 55 70 New
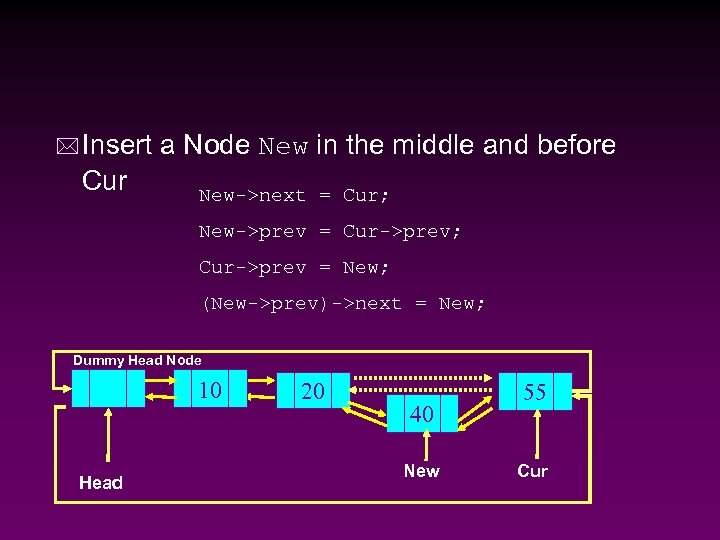
* Insert a Node New in the middle and before Cur New->next = Cur; New->prev = Cur->prev; Cur->prev = New; (New->prev)->next = New; Dummy Head Node 10 Head 20 40 New 55 Cur
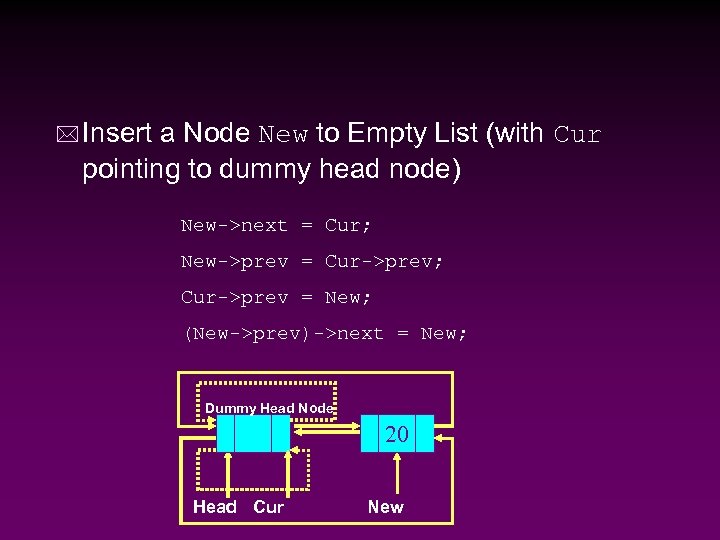
* Insert a Node New to Empty List (with Cur pointing to dummy head node) New->next = Cur; New->prev = Cur->prev; Cur->prev = New; (New->prev)->next = New; Dummy Head Node 20 Head Cur New
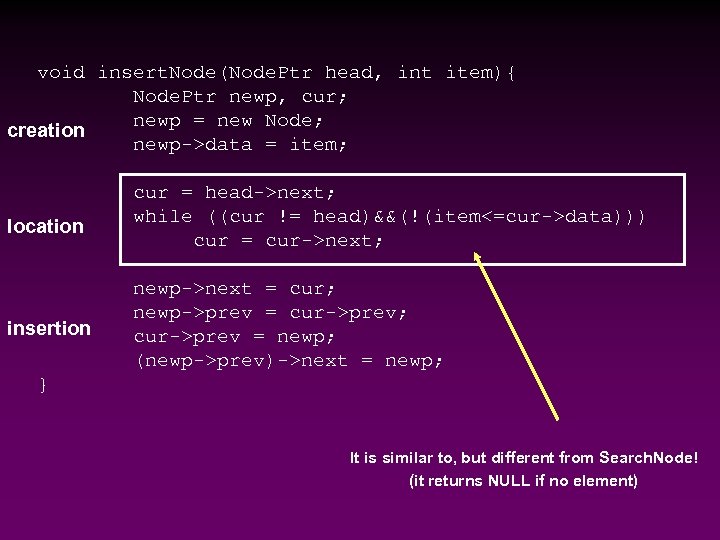
void insert. Node(Node. Ptr head, int item){ Node. Ptr newp, cur; newp = new Node; creation newp->data = item; location cur = head->next; while ((cur != head)&&(!(item<=cur->data))) cur = cur->next; insertion newp->next = cur; newp->prev = cur->prev; cur->prev = newp; (newp->prev)->next = newp; } It is similar to, but different from Search. Node! (it returns NULL if no element)
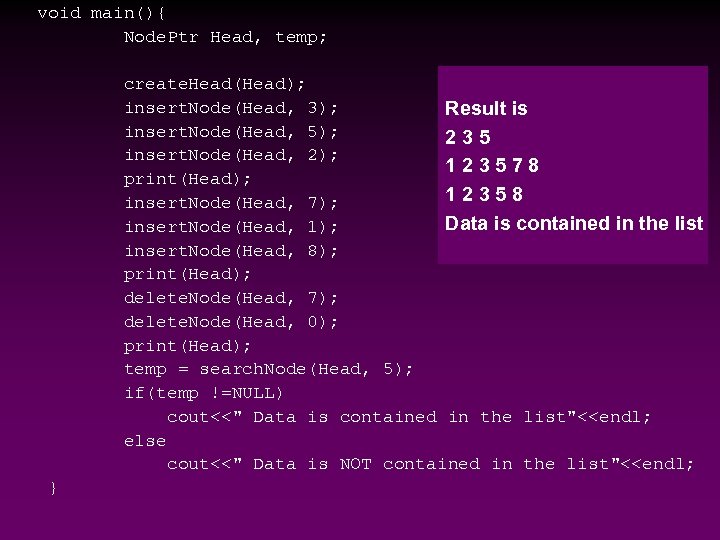
void main(){ Node. Ptr Head, temp; create. Head(Head); insert. Node(Head, 3); Result is insert. Node(Head, 5); 235 insert. Node(Head, 2); 123578 print(Head); 12358 insert. Node(Head, 7); Data is contained in the list insert. Node(Head, 1); insert. Node(Head, 8); print(Head); delete. Node(Head, 7); delete. Node(Head, 0); print(Head); temp = search. Node(Head, 5); if(temp !=NULL) cout<<" Data is contained in the list"<<endl; else cout<<" Data is NOT contained in the list"<<endl; }

Stacks and Queues
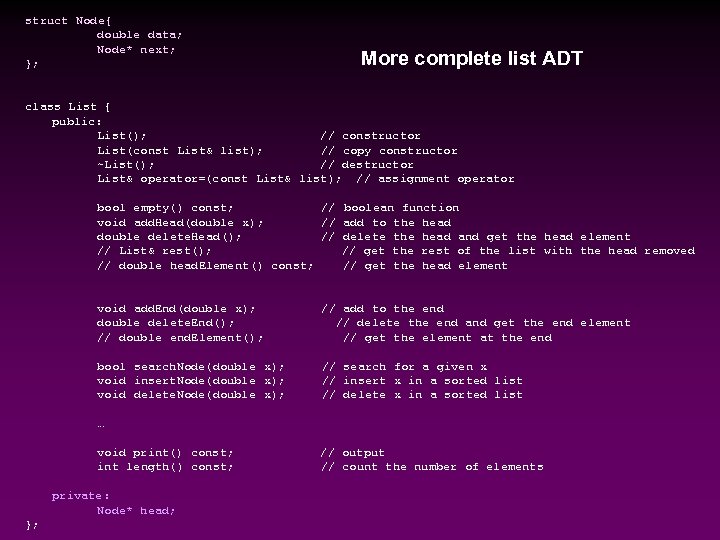
struct Node{ double data; Node* next; }; More complete list ADT class List { public: List(); // constructor List(const List& list); // copy constructor ~List(); // destructor List& operator=(const List& list); // assignment operator bool empty() const; // boolean function void add. Head(double x); // add to the head double delete. Head(); // delete the head and get the head element // List& rest(); // get the rest of the list with the head removed // double head. Element() const; // get the head element void add. End(double x); double delete. End(); // double end. Element(); // add to the end // delete the end and get the end element // get the element at the end bool search. Node(double x); void insert. Node(double x); void delete. Node(double x); // search for a given x // insert x in a sorted list // delete x in a sorted list … void print() const; int length() const; private: Node* head; }; // output // count the number of elements

Stack Overview * Stack ADT * Basic operations of stack n Pushing, popping etc. * Implementations of stacks using array n linked list n

Stack * A stack is a list in which insertion and deletion take place at the same end This end is called top n The other end is called bottom n * Stacks are known as LIFO (Last In, First Out) lists. n The last element inserted will be the first to be retrieved

Push and Pop * Primary operations: Push and Pop * Push n Add an element to the top of the stack * Pop n Remove the element at the top of the stack empty stack push an element top top A push another B A pop top A

Implementation of Stacks * Any list implementation could be used to implement a stack Arrays (static: the size of stack is given initially) n Linked lists (dynamic: never become full) n * We will explore implementations based on array and linked list

Stack ADT class Stack { public: Stack(); // constructor Stack(const Stack& stack); // copy constructor ~Stack(); // destructor bool empty() const; void push(const double x); double pop(); // change the stack double top() const; // bool full(); // void print() const; // keep the stack unchanged inspection, access // optional private: … }; Compare with List, see that it’s ‘operations’ that define the type!
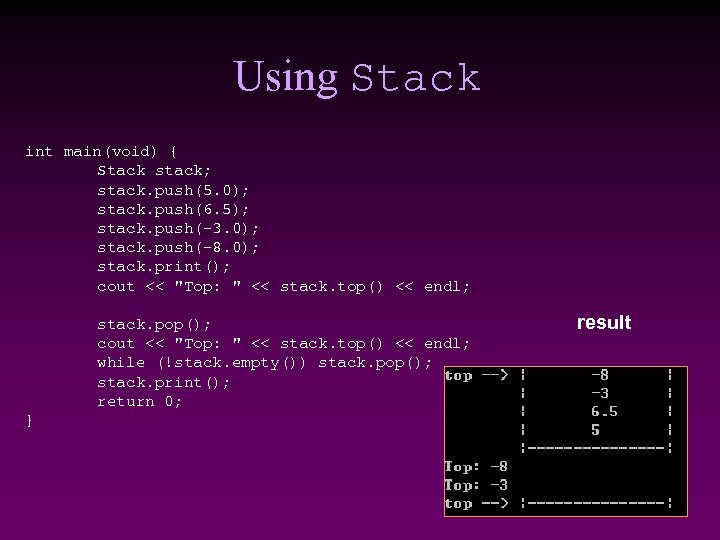
Using Stack int main(void) { Stack stack; stack. push(5. 0); stack. push(6. 5); stack. push(-3. 0); stack. push(-8. 0); stack. print(); cout << "Top: " << stack. top() << endl; stack. pop(); cout << "Top: " << stack. top() << endl; while (!stack. empty()) stack. pop(); stack. print(); return 0; } result
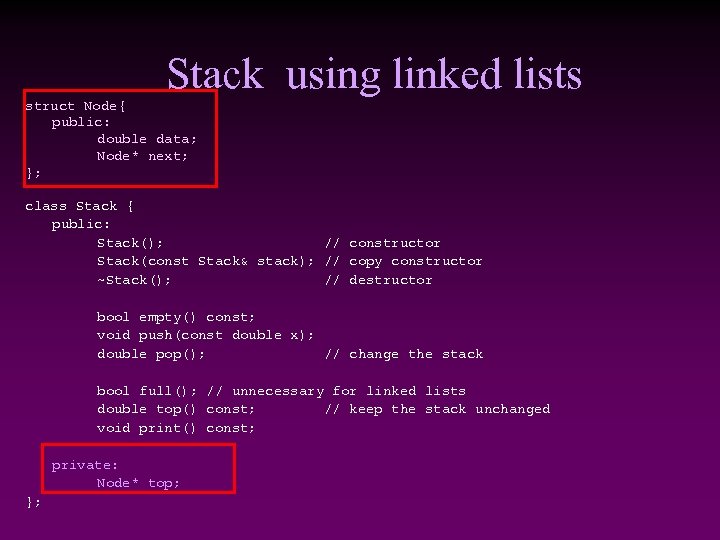
Stack using linked lists struct Node{ public: double data; Node* next; }; class Stack { public: Stack(); // constructor Stack(const Stack& stack); // copy constructor ~Stack(); // destructor bool empty() const; void push(const double x); double pop(); // change the stack bool full(); // unnecessary for linked lists double top() const; // keep the stack unchanged void print() const; private: Node* top; };
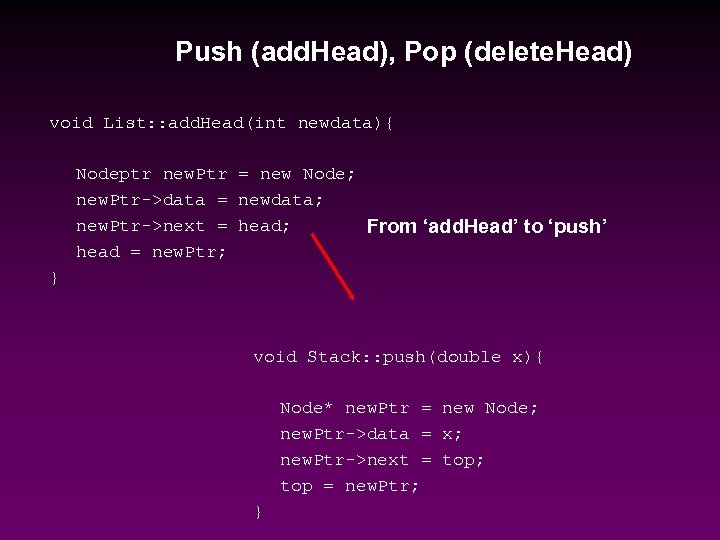
Push (add. Head), Pop (delete. Head) void List: : add. Head(int newdata){ Nodeptr new. Ptr = new Node; new. Ptr->data = newdata; new. Ptr->next = head; From ‘add. Head’ to ‘push’ head = new. Ptr; } void Stack: : push(double x){ Node* new. Ptr = new Node; new. Ptr->data = x; new. Ptr->next = top; top = new. Ptr; }

Implementation based on ‘existing’ linked lists * Optional to learn * Good to see that we may ‘re-use’ linked lists
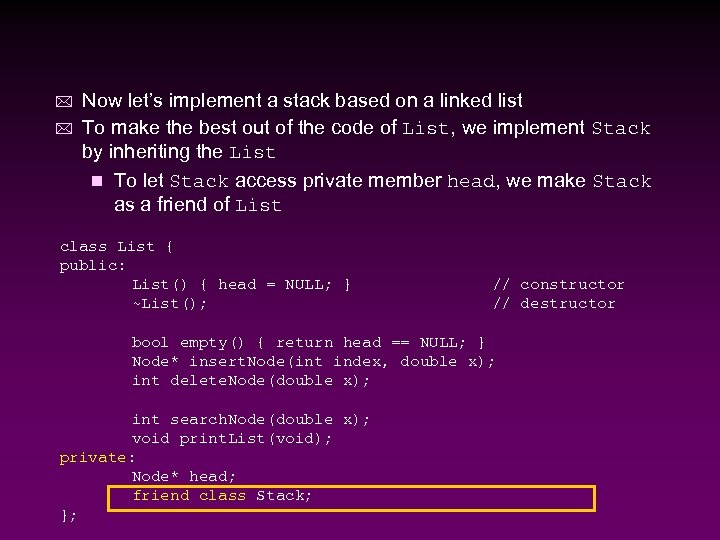
* * Now let’s implement a stack based on a linked list To make the best out of the code of List, we implement Stack by inheriting the List n To let Stack access private member head, we make Stack as a friend of List class List { public: List() { head = NULL; } ~List(); // constructor // destructor bool empty() { return head == NULL; } Node* insert. Node(int index, double x); int delete. Node(double x); int search. Node(double x); void print. List(void); private: Node* head; friend class Stack; };
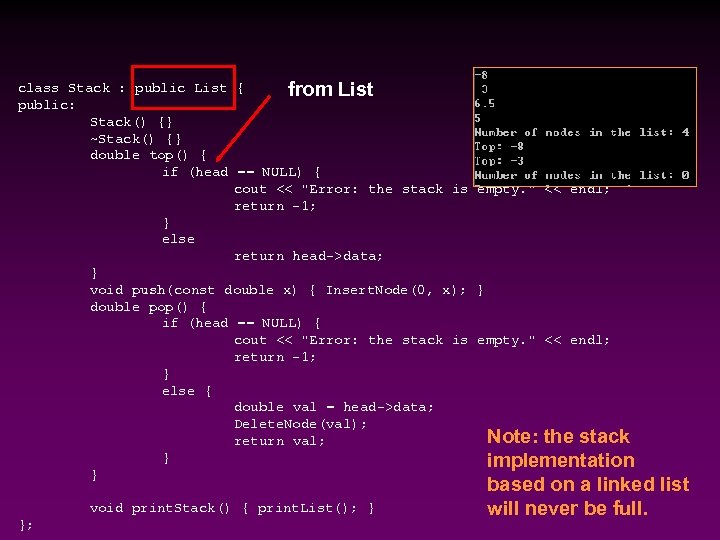
class Stack : public List { from List public: Stack() {} ~Stack() {} double top() { if (head == NULL) { cout << "Error: the stack is empty. " << endl; return -1; } else return head->data; } void push(const double x) { Insert. Node(0, x); } double pop() { if (head == NULL) { cout << "Error: the stack is empty. " << endl; return -1; } else { double val = head->data; Delete. Node(val); Note: the stack return val; } implementation } void print. Stack() { print. List(); } }; based on a linked list will never be full.
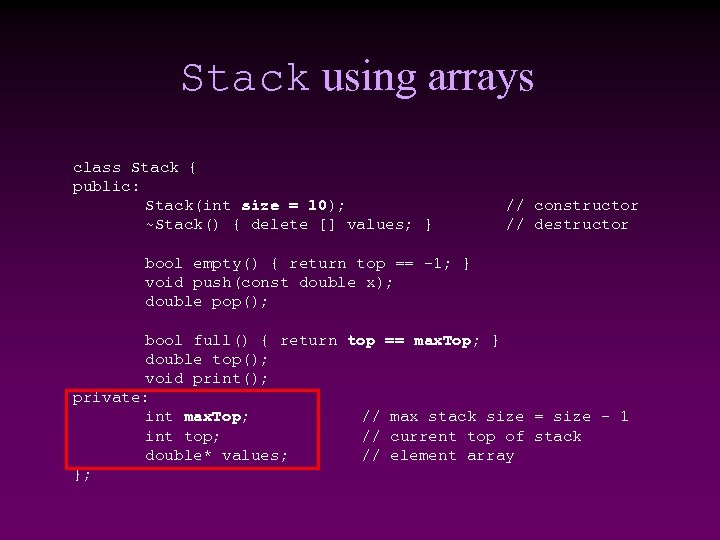
Stack using arrays class Stack { public: Stack(int size = 10); ~Stack() { delete [] values; } // constructor // destructor bool empty() { return top == -1; } void push(const double x); double pop(); bool full() { return top == max. Top; } double top(); void print(); private: int max. Top; // max stack size = size - 1 int top; // current top of stack double* values; // element array };

* Attributes of Stack max. Top: the max size of stack n top: the index of the top element of stack n values: point to an array which stores elements of stack n * Operations of Stack n n n empty: return true if stack is empty, return false otherwise full: return true if stack is full, return false otherwise top: return the element at the top of stack push: add an element to the top of stack pop: delete the element at the top of stack print: print all the data in the stack

Stack constructor Allocate a stack array of size. By default, size = 10. n Initially top is set to -1. It means the stack is empty. n When the stack is full, top will have its maximum value, i. e. n size – 1. Stack: : Stack(int size /*= 10*/) { values = new double[size]; top = -1; max. Top = size - 1; } Although the constructor dynamically allocates the stack array, the stack is still static. The size is fixed after the initialization.

* void push(const double x); Push an element onto the stack n Note top always represents the index of the top element. After pushing an element, increment top. n void Stack: : push(const double x) { if (full()) // if stack is full, print error cout << "Error: the stack is full. " << endl; else values[++top] = x; }

* double pop() Pop and return the element at the top of the stack n Don’t forgot to decrement top n double Stack: : pop() { if (empty()) { //if stack is empty, print error cout << "Error: the stack is empty. " << endl; return -1; } else { return values[top--]; } }

* double top() Return the top element of the stack n Unlike pop, this function does not remove the top element n double Stack: : top() { if (empty()) { cout << "Error: the stack is empty. " << endl; return -1; } else return values[top]; }
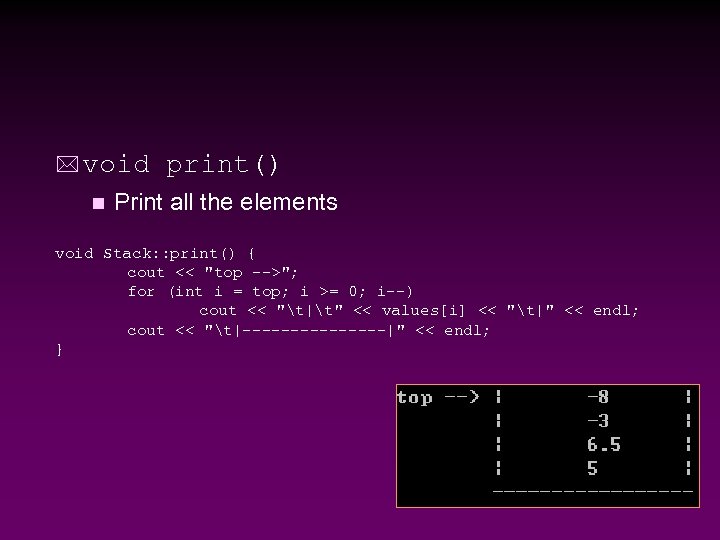
* void n print() Print all the elements void Stack: : print() { cout << "top -->"; for (int i = top; i >= 0; i--) cout << "t|t" << values[i] << "t|" << endl; cout << "t|--------|" << endl; }

Stack Application: Balancing Symbols * To check that every right brace, bracket, and parentheses must correspond to its left counterpart n e. g. [( )] is legal, but [( ] ) is illegal * How? Need to memorize n Use a counter, several counters, each for a type of parenthesis … n

Balancing Symbols using a stack * Algorithm (1) Make an empty stack. (2) Read characters until end of file i. If the character is an opening symbol, push it onto the stack ii. If it is a closing symbol, then if the stack is empty, report an error iii. Otherwise, pop the stack. If the symbol popped is not the corresponding opening symbol, then report an error (3) At end of file, if the stack is not empty, report an error

Stack Application: postfix, infix expressions and calculator * Postfix expressions a b c * + d e * f + g * + n Operands are in a stack n * Convert infix to postfix a+b*c+(d*e+f)*g a b c * + d e * f + g * + n Operators are in a stack n * Calculator n Adding more operators …

Stack Application: function calls and recursion * Take the example of factorial! And run it. #include <iostream> using namespace std; int fac(int n){ int product; if(n <= 1) product = 1; else product = n * fac(n-1); return product; } void main(){ int number; cout << "Enter a positive integer : " << endl; ; cin >> number; cout << fac(number) << endl; }

Stack Application: function calls and recursion * Take the example of factorial! And run it. #include <iostream> using namespace std; int fac(int n){ int product; if(n <= 1) product = 1; else product = n * fac(n-1); return product; } void main(){ int number; cout << "Enter a positive integer : " << endl; ; cin >> number; cout << fac(number) << endl; }

Tracing the program … Assume the number typed is 3. fac(3): 3<=1 ? No. product 3 = 3*fac(2): 2<=1 ? No. product 2 = 2*fac(1): 1<=1 ? Yes. return 1 has the final returned value 6 product 3=3*2=6, return 6, product 2=2*1=2, return 2,

Call is to ‘push’ and return is to ‘pop’! top fac(1) prod 1=1 fac(2) prod 2=2*fac(1) fac(3) prod 3=3*fac(2)

Array versus linked list implementations * push, pop, top are all constant-time operations in both array and linked list implementation Caveat: insert. Node and delete. Node have to be done at the beginning of the list! n For array implementation, the operations are performed in very fast constant time n

Queue Overview * Queue ADT * Basic operations of queue n Enqueuing, dequeuing etc. * Implementation of queue Linked list n Array n

Queue * A queue is also a list. However, insertion is done at one end, while deletion is performed at the other end. * It is “First In, First Out (FIFO)” order. n Like customers standing in a check-out line in a store, the first customer in is the first customer served.

Enqueue and Dequeue * Primary queue operations: Enqueue and Dequeue * Like check-out lines in a store, a queue has a front and a rear. * Enqueue – insert an element at the rear of the queue * Dequeue – remove an element from the front of the queue Remove (Dequeue) front rear Insert (Enqueue)

Implementation of Queue * Just as stacks can be implemented as arrays or linked lists, so with queues. * Dynamic queues have the same advantages over static queues as dynamic stacks have over static stacks * (“static” should be interpreted as “non-dynamic” here!)
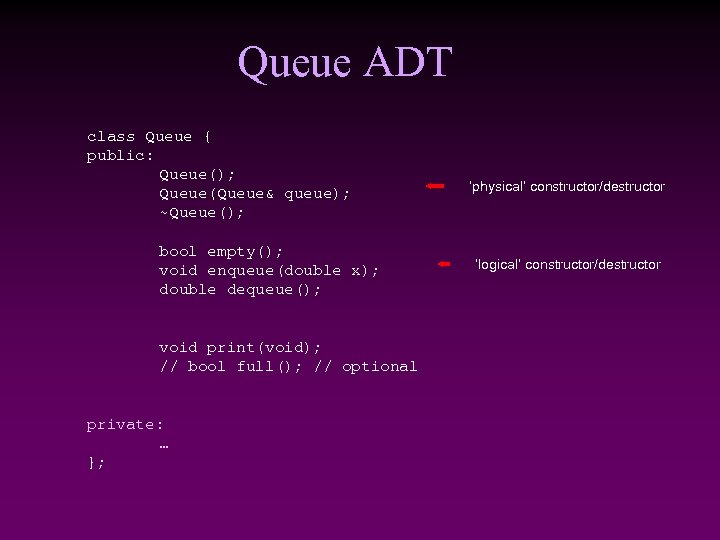
Queue ADT class Queue { public: Queue(); Queue(Queue& queue); ~Queue(); bool empty(); void enqueue(double x); double dequeue(); void print(void); // bool full(); // optional private: … }; ‘physical’ constructor/destructor ‘logical’ constructor/destructor
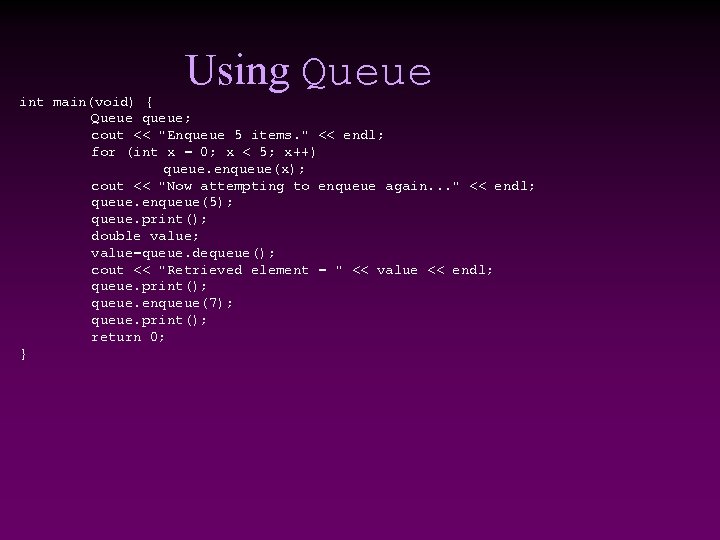
Using Queue int main(void) { Queue queue; cout << "Enqueue 5 items. " << endl; for (int x = 0; x < 5; x++) queue. enqueue(x); cout << "Now attempting to enqueue again. . . " << endl; queue. enqueue(5); queue. print(); double value; value=queue. dequeue(); cout << "Retrieved element = " << value << endl; queue. print(); queue. enqueue(7); queue. print(); return 0; }
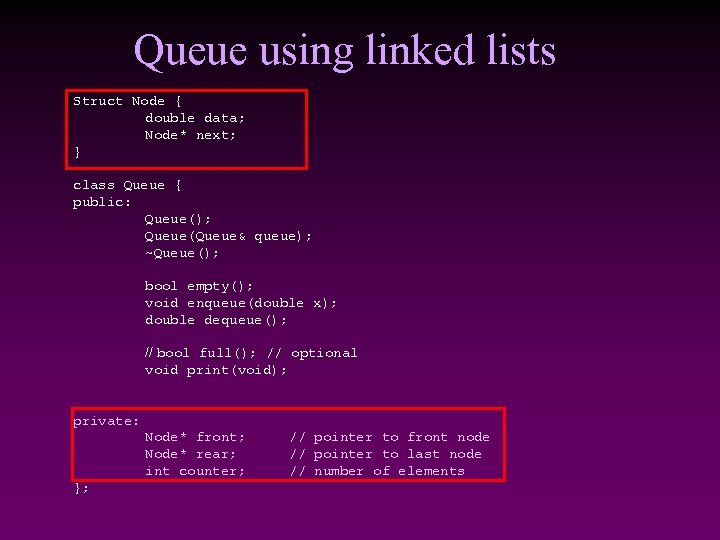
Queue using linked lists Struct Node { double data; Node* next; } class Queue { public: Queue(); Queue(Queue& queue); ~Queue(); bool empty(); void enqueue(double x); double dequeue(); // bool full(); // optional void print(void); private: Node* front; Node* rear; int counter; }; // pointer to front node // pointer to last node // number of elements

Implementation of some online member functions … class Queue { public: Queue() { // constructor front = rear = NULL; counter = 0; } ~Queue() { // destructor double value; while (!empty()) dequeue(value); } bool empty() { if (counter) return false; else return true; } void enqueue(double x); double dequeue(); // bool full() {return false; }; void print(void); private: Node* front; Node* rear; int counter; }; // pointer to front node // pointer to last node // number of elements, not compulsary

Enqueue (add. End) void Queue: : enqueue(double x) { Node* new. Node = new Node; new. Node->data = x; new. Node->next = NULL; if (empty()) { front = new. Node; } else { rear->next = new. Node; } rear 5 8 rear = new. Node; counter++; } 8 5 new. Node
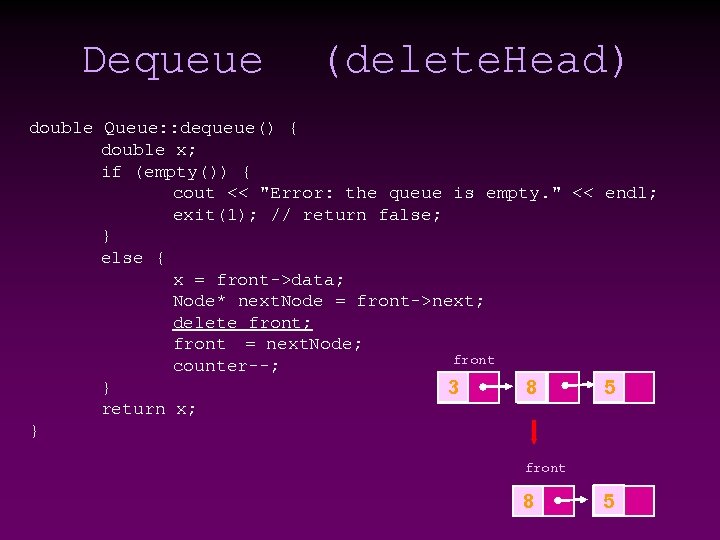
Dequeue (delete. Head) double Queue: : dequeue() { double x; if (empty()) { cout << "Error: the queue is empty. " << endl; exit(1); // return false; } else { x = front->data; Node* next. Node = front->next; delete front; front = next. Node; front counter--; } 3 8 5 return x; } front 8 5

Printing all the elements void Queue: : print() { cout << "front -->"; Node* curr. Node = front; for (int i = 0; i < counter; i++) { if (i == 0) cout << "t"; else cout << "tt"; cout << curr. Node->data; if (i != counter - 1) cout << endl; else cout << "t<-- rear" << endl; curr. Node = curr. Node->next; } }
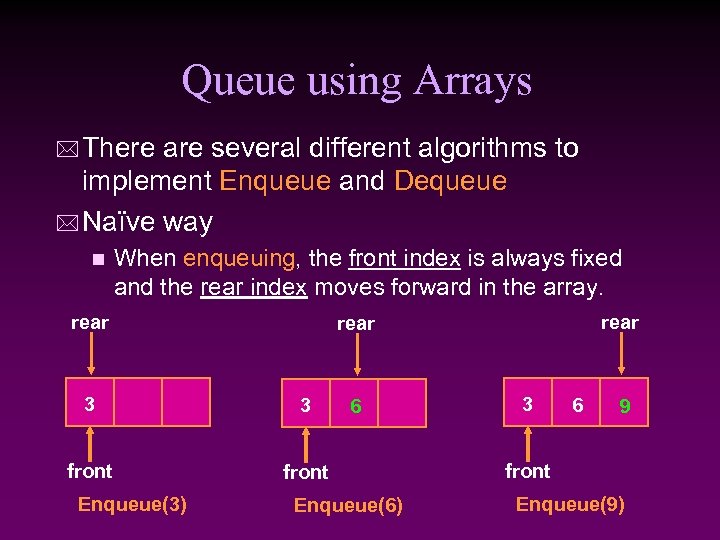
Queue using Arrays * There are several different algorithms to implement Enqueue and Dequeue * Naïve way n When enqueuing, the front index is always fixed and the rear index moves forward in the array. rear 3 3 front Enqueue(3) rear 6 Enqueue(6) 3 6 9 front Enqueue(9)
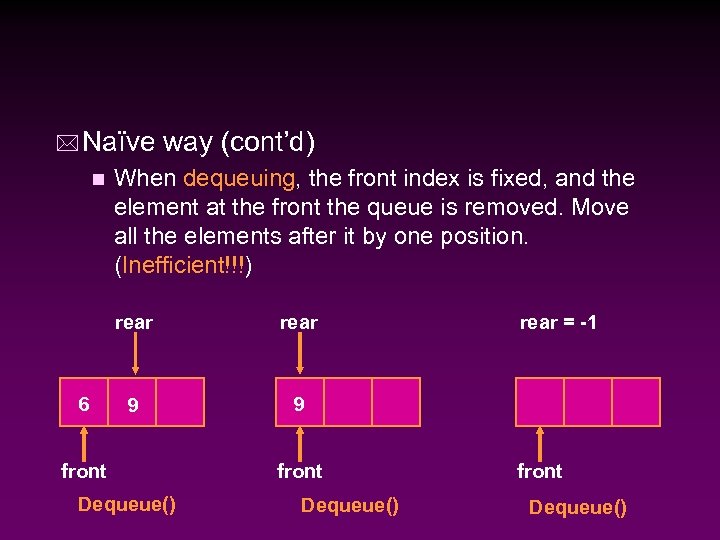
* Naïve way (cont’d) n When dequeuing, the front index is fixed, and the element at the front the queue is removed. Move all the elements after it by one position. (Inefficient!!!) rear 6 rear 9 9 front Dequeue() rear = -1 front Dequeue()

* A better way When enqueued, the rear index moves forward. n When dequeued, the front index also moves forward by one element n (front) XXXXOOOOO (rear) OXXXXOOOO (after 1 dequeue, and 1 enqueue) OOXXXXXOO (after another dequeue, and 2 enqueues) OOOOXXXXX (after 2 more dequeues, and 2 enqueues) The problem here is that the rear index cannot move beyond the last element in the array.

Using Circular Arrays * Using a circular array * When an element moves past the end of a circular array, it wraps around to the beginning, e. g. n OOOOO 7963 4 OOOO 7963 (after Enqueue(4)) * How to detect an empty or full queue, using a circular array algorithm? n Use a counter of the number of elements in the queue.
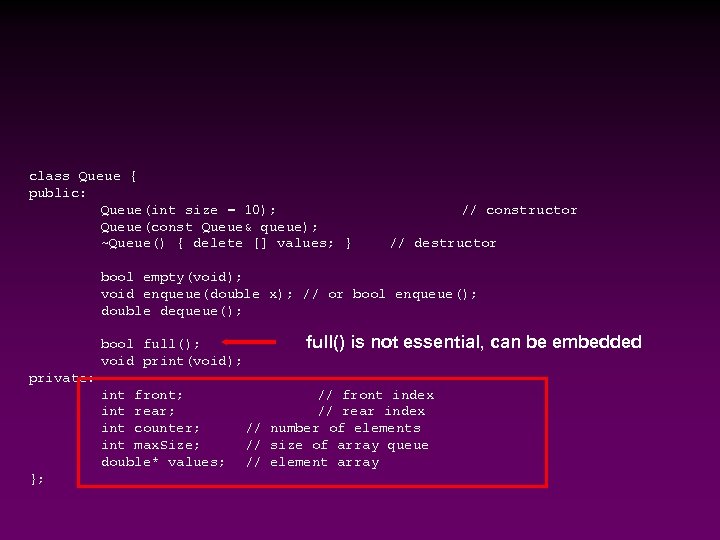
class Queue { public: Queue(int size = 10); Queue(const Queue& queue); ~Queue() { delete [] values; } // constructor // destructor bool empty(void); void enqueue(double x); // or bool enqueue(); double dequeue(); bool full(); void print(void); full() is not essential, can be embedded private: int front; int rear; int counter; int max. Size; double* values; }; // front index // rear index // number of elements // size of array queue // element array

* Attributes of Queue front/rear: front/rear index n counter: number of elements in the queue n max. Size: capacity of the queue n values: point to an array which stores elements of the queue n * Operations of Queue n n n empty: return true if queue is empty, return false otherwise full: return true if queue is full, return false otherwise enqueue: add an element to the rear of queue dequeue: delete the element at the front of queue print: print all the data

Queue constructor * Queue(int size = 10) Allocate a queue array of size. By default, size = 10. n front is set to 0, pointing to the first element of the array n rear is set to -1. The queue is empty initially. n Queue: : Queue(int size /* = 10 */) { values = new double[size]; max. Size = size; front = 0; rear = -1; counter = 0; }

Empty & Full * Since we keep track of the number of elements that are actually in the queue: counter, it is easy to check if the queue is empty or full. bool Queue: : empty() { if (counter==0) return else return } bool Queue: : full() { if (counter < max. Size) else } true; false; return true;

Enqueue Or ‘bool’ if you want void Queue: : enqueue(double x) { if (full()) { cout << "Error: the queue is full. " << endl; exit(1); // return false; } else { // calculate the new rear position (circular) rear = (rear + 1) % max. Size; // insert new item values[rear] = x; // update counter++; // return true; } }
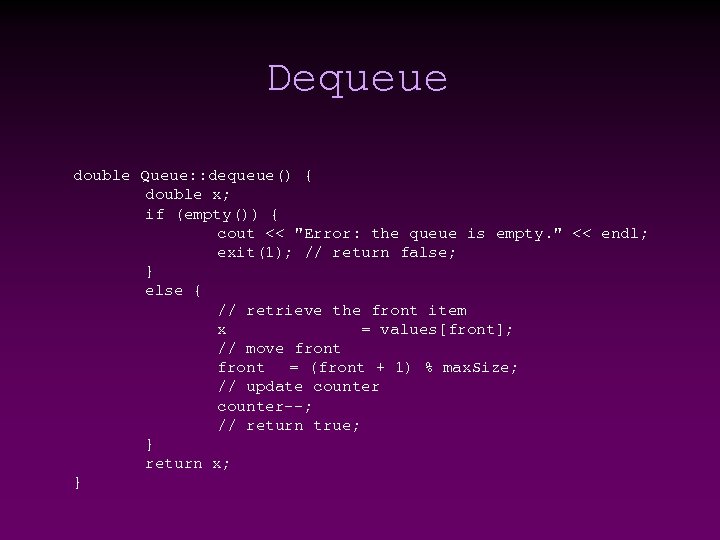
Dequeue double Queue: : dequeue() { double x; if (empty()) { cout << "Error: the queue is empty. " << endl; exit(1); // return false; } else { // retrieve the front item x = values[front]; // move front = (front + 1) % max. Size; // update counter--; // return true; } return x; }

Printing the elements void Queue: : print() { cout << "front -->"; for (int i = 0; i < counter; i++) { if (i == 0) cout << "t"; else cout << "tt"; cout << values[(front + i) % max. Size]; if (i != counter - 1) cout << endl; else cout << "t<-- rear" << endl; } }
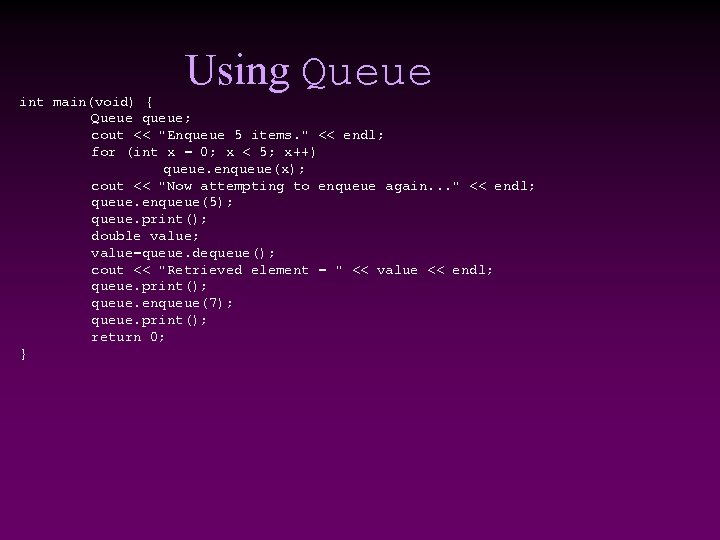
Using Queue int main(void) { Queue queue; cout << "Enqueue 5 items. " << endl; for (int x = 0; x < 5; x++) queue. enqueue(x); cout << "Now attempting to enqueue again. . . " << endl; queue. enqueue(5); queue. print(); double value; value=queue. dequeue(); cout << "Retrieved element = " << value << endl; queue. print(); queue. enqueue(7); queue. print(); return 0; }

Results based on array based on linked list Queue implemented using linked list will be never full!

Queue applications * When jobs are sent to a printer, in order of arrival, a queue. * Customers at ticket counters …
55609622901f395e48aea12047a26851.ppt