Liquids and Gases The unit of volume is

Liquids and Gases The unit of volume is the meter cubed , m 3, which is a very large volume. Very often we use cm 3 = cc, or Litres = 103 cc Other everyday units are gallons, quarts, pints 1 qt = 2 lbs H 2 O, 1 L = 2. 2 lbs H 2 O = 1 kg H 2 O As we know liquids and gases (fluids) act very differently than solids. Liquids and gases have mass but their constituent atoms are not rigidly bound. Therefore each part of the liquid or gas can move. The atoms of a liquid are more tightly bound so a liquid can be kept in an open container whereas gas usually requires a closed container. Liquids, like solids are not very compressible, that is, it is difficult to change the volume. The volume of a gas can be changed fairly easily by changing the pressure. Both liquids and gases have the property of being able to flow, Hence the name “fluid”. For example water and gas lines in a house. Feb. 25 -29, 2008 Physics 214 Spring 2007 1

Pressure A volume of liquid or gas has mass and F = ma is still a good law, except if we exert a force at a point on, say, the surface of water in a container, only the water near the point moves, and that movement is quite complicated. So generally we work with liquids and gases in containers and exert forces over a surface. We define pressure as P = F/A “force per unit area” that is, the force divided by the area over which the force acts. Any change in pressure is transmitted uniformly throughout a liquid. Units are N/m 2 Feb. 25 -29, 2008 1 N/m 2 = 1 Pascal Physics 214 Spring 2007 2

Hydraulic Jack If the liquid levels on each side are the same height then the pressure just below each piston is the same and F 1/A 1 = F 2/A 2 so F 2 = F 1 A 2/A 1 If we make A 2/A 1 = 100 then an F 1 force of 50 lbs can lift 5000 lbs. Of course if we push F 1 down a distance h 1 then the F 2 Side will only rise h 2=h 1 A 1/A 2 because h 1 A 1 = Vol. = h 2 A 2, that is, the displaced volumes must be the same. Work done = F 1 h 1 = F 2 h 2 Like a lever, the small force works over the long distance and vice versa. Feb. 25 -29, 2008 Physics 214 Spring 2007 3

Atmospheric pressure If I stack a pile of bricks each brick has to support all the bricks above it. So as We go down the stack the force increases, as does the pressure. In the example shown the force on the face of the bottom brick would be 6 mg and the pressure = 6 mg/A, where A is the area of contact g F At the earths surface we are supporting a column of air which exerts a weight force. Because it is a gas the air exerts an equal pressure In all directions. This pressure comes from the weight of air above a given horizontal area. Feb. 25 -29, 2008 Physics 214 Spring 2007 4

Density If one takes two objects of exactly the same volume made of different materials they usually have different weights. So we define a useful quantity ρ (rho) Density ρ = mass/unit volume, kg/m 3 or grams/cc so the mass of an object is M= ρV and the weight is W= ρVg If an object is put into a container of liquid it will float if ρobject is less than ρliquid It will sink if ρobject is greater than ρliquid Feb. 25 -29, 2008 Physics 214 Spring 2007 5

Density and pressure In a container of liquid the pressure at any depth is the weight of the column of water above that depth divided by the horizontal area of the column. (Relative to the surface, where the pressure is typically one atmosphere. ) g Mass/unit volume ρ = kg/m 3. Other times we use grams/cubic centimeter 1 gram/cm 3 = 1000 kg/m 3 ρwater is 1 gram/cc or 1 Ton/m 3 , where we mean Metric Ton (= 103 kg) Column weighs W = mg = ρAhg Pressure P = W/A = ρgh. P increases with depth. At a given depth, pressure is uniform (and omnidirectional. ) Start with atmospheric pressure at the top surface of the liquid. Feb. 25 -29, 2008 Physics 214 Spring 2007 6

Effects of Atmospheric Pressure In our everyday lives we do not feel that we are supporting a very large weight because it is the environment in which we developed. Also the pressure is almost the same inside our lungs, and inside our ears, as it is outside us. If we fill a tube with a liquid so that all the air bubbles are removed and then we raise the tube to a vertical position we find that atmospheric pressure supports 76 cm of mercury or 33 feet of water. No Air g Knowing the weight of the Mercury and the area of the tube we find that 1 Atmosphere = 1. 013 105 Pa This is equal to ρgh for the Mercury, so all we actually need to know is h, and ρHg=13. 534 gm/cc , (and g) Feb. 25 -29, 2008 Physics 214 Spring 2007 P is the same 7

Everyday examples v Suction cups – remove the air and the atmosphere holds it in place. v Drinking through a straw – create a partial vacuum in your mouth and the atmospheric pressure pushes the fluid up the straw v Impossible to suck water higher than 33 ft, can’t have less than a vacuum at the top (except in tree sap channels, where water is IN TENSION – effectively a negative pressure) v Air pressure is lower at higher altitudes – water boils at a lower temperature v Pressure is higher the deeper you go in the ocean – leads to more nitrogen being absorbed in blood, and the bends. Also raises boiling point of water (hot vents at midocean ridges, weird critters there) Feb. 25 -29, 2008 Physics 214 Spring 2007 8

Suction cup Question: What is the minimum area of a suction cup that can be used to lift 100 kg. The suction cup will stay attached to the block providing PA is greater than F/A. In practice there would only be a partial vacuum under the cup so the cup would break away from the block at a lower force and pressure. 1. 013 x 105 N/m 2 x A = W = 100 kgx 9. 8 m/s 2 = 980 N A = 980/101, 300(N/m 2)/N =. 00967 m 2 or 96. 7 cm 2 This would be a circle of diameter just over 4 inches Feb. 25 -29, 2008 Physics 214 Spring 2007 F PA mg 9

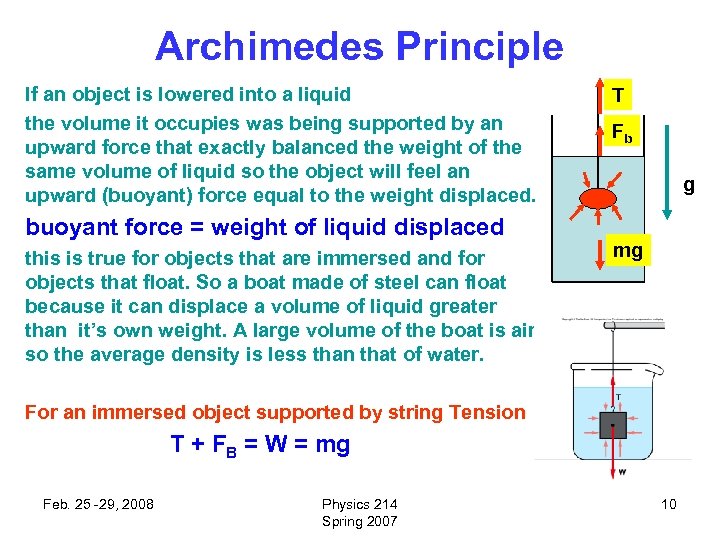Archimedes Principle If an object is lowered into a liquid the volume it occupies was being supported by an upward force that exactly balanced the weight of the same volume of liquid so the object will feel an upward (buoyant) force equal to the weight displaced. buoyant force = weight of liquid displaced this is true for objects that are immersed and for objects that float. So a boat made of steel can float because it can displace a volume of liquid greater than it’s own weight. A large volume of the boat is air so the average density is less than that of water. T Fb g mg For an immersed object supported by string Tension T + FB = W = mg Feb. 25 -29, 2008 Physics 214 Spring 2007 10

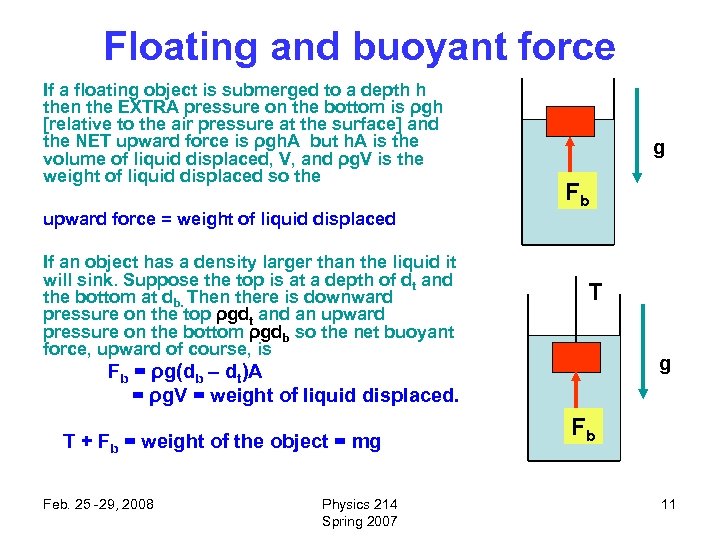Floating and buoyant force If a floating object is submerged to a depth h then the EXTRA pressure on the bottom is ρgh [relative to the air pressure at the surface] and the NET upward force is ρgh. A but h. A is the volume of liquid displaced, V, and ρg. V is the weight of liquid displaced so the upward force = weight of liquid displaced If an object has a density larger than the liquid it will sink. Suppose the top is at a depth of dt and the bottom at db. Then there is downward pressure on the top ρgdt and an upward pressure on the bottom ρgdb so the net buoyant force, upward of course, is g Fb T g Fb = ρg(db – dt)A = ρg. V = weight of liquid displaced. T + Fb = weight of the object = mg Feb. 25 -29, 2008 Physics 214 Spring 2007 Fb 11

Floating and buoyant force Water ice is LESS dense than liquid water (by about 10%). Water is a very ususual substance. Upward force = weight of liquid displaced So ice floats in water with about 10% of its volume above the water level. If the red “ice cube” melts, THE WATER LEVEL WILL NOT CHANGE. If floating sea ice melts (like the Arctic) the sea level will not change. If ice ON LAND melts, (Greenland, West Antarctic) sea level WILL rise. ~20 feet each!! There’s enough ice on land right now to raise sea level roughly 100 meters (300 feet). It wouldn’t even have to melt, if it slid off into the sea and floated!! (Greenland? ? ***** Break for web pages ***** Feb. 25 -29, 2008 Physics 214 Spring 2007 g Fb 12

Pressure and Volume of a Gas In the apparatus shown the pressure at point A is the same as at point B. First example: volume V 1 is at atmospheric pressure. Second example, more mercury is added. The extra height of mercury adds ρgh to the pressure at (new) point A. The new volume, V 2, is less. It feels a total pressure of 1 Atmosphere + ρgh g h A A B B If the temperature does not change we find PV = constant Feb. 25 -29, 2008 Physics 214 Spring 2007 13

Fluids in motion Liquid flow in a pipe: speed x cross sectional area is constant due to “conservation of volume” (incompressibility) A 1 v 1 = A 2 v 2 A 1 v 2 A 2 Feb. 25 -29, 2008 Physics 214 Spring 2007 14

Fluids in motion Liquid flow – Bernoulli’s Principle PV (Pressure x Volume) has units of energy, and represents Potential Energy stored in a given volume of liquid. Bernoulli realized that if the flow is streamlined, and we can neglect drag, the Mech. Energy of the liquid, which is KE + PE, is conserved. Faster liquid has greater KE, therefore it MUST have lower PE and hence, lower Pressure. DEMOS (F/A)V : [N/m 2]x m 3 = [Nm] = [Joules] Feb. 25 -29, 2008 Physics 214 Spring 2007 A 1 v 2 A 2 15

ANNOUNCEMENT BONUS and MAKEUP POLICY ONE-HALF OF YOUR FINAL EXAM SCORE WILL REPLACE YOUR LOWEST HOUR-EXAM SCORE, IF THAT IS TO YOUR ADVANTAGE (i. e. if that amount is MORE than your lowest hour-exam score) This will also be the “makeup” score for an EXCUSED missed hour-exam. Example: T 1 05 points T 2 75 Final 160/2=80, 80 replaces worst score so T 1 becomes 80 Feb. 25 -29, 2008 Physics 214 Spring 2007 16

Summary of Chapter 9 P = F/A Pascals or N/m 2 P = 1 Atm + ρgh F 1/A 1 = F 2/A 2 Work done = F 1 h 1 = F 2 h 2 1 Atmosphere = 1. 013 105 Pa = 101. 3 k. Pa (kilo. Pascals) and will support 76 cm of mercury 33 feet of water Feb. 25 -29, 2008 No Air g Physics 214 Spring 2007 17

Summary: Liquids P = W/A = ρgh + pressure at top of liquid Water density is 1 gram/cc 1 gram/cm 3 = 1000 kg/m 3 = 1 Ton/m 3 T buoyant force = the weight of liquid displaced T + FB = W = mg Fb T = external support force g For a floating object T = 0 mg Feb. 25 -29, 2008 Physics 214 Spring 2007 18

Summary Fluids in motion Liquid flow in a pipe: speed x cross sectional area is constant due to “conservation of volume” (incompressibility) A 1 v 1 = A 2 v 2 A 1 v 2 A 2 Feb. 25 -29, 2008 Physics 214 Spring 2007 19

Summary: Bernoulli’s Principle WHEN A FLUID SPEEDS UP, ITS PRESSURE DROPS. A 1 P v 1 Faster-flowing liquid has greater KE, therefore it MUST have lower PE and hence, lower Pressure. PV = (F/A)V [N/m 2]x m 3 = [Nm] = [Joules] v 2 p This is true not only for flow in tubes, but for wings, sails, boat keels, etc. (these “free” objects can experience “lift”) A 2 Feb. 25 -29, 2008 20 Physics 214 Spring 2007

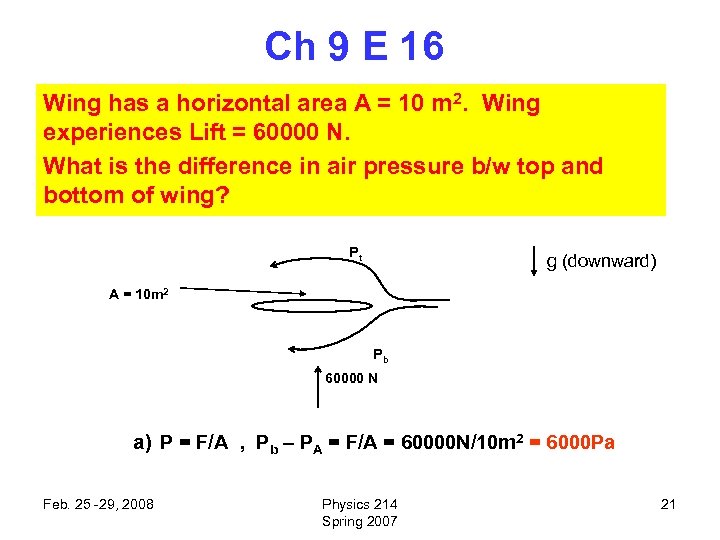Ch 9 E 16 Wing has a horizontal area A = 10 m 2. Wing experiences Lift = 60000 N. What is the difference in air pressure b/w top and bottom of wing? Pt g (downward) A = 10 m 2 Pb 60000 N a) P = F/A , Pb – PA = F/A = 60000 N/10 m 2 = 6000 Pa Feb. 25 -29, 2008 Physics 214 Spring 2007 21

2 A-03 Vacuum Demos Effects of Vacuum on objects made largely of air or air pockets. Why do the balloons burst in the vacuum ? Why do the marshmallows get bigger in vacuum ? Do the balloons burst in vacuum differently then they normally burst ? What will happen when the marshmallows are returned to normal pressure ? Can you guess what happens when Shaving Cream is placed in vacuum ? AN AIR-POCKET/BALLOON WILL EXPAND WHEN THE PRESSURE IS REDUCED AND IT WILL DEFLATE WHEN THE PRESSURE IS INCREASED. SO BALLOONS WILL EXPAND AS THEY RISE IN THE ATMOSHPERE AND THE EXPANSION OF A PARTIALLY EVACUATED CAN IS USED IN BAROMETERS. Feb. 25 -29, 2008 Physics 214 Spring 2007 22

Q 11 If you filled an airtight balloon at the top of a mountain, would the balloon expand or contract as you descend the mountain? It would contract because the atmospheric pressure would increase and the pressure inside the balloon would increase to balance this change Q 12 When you go over a mountain pass in an automobile, your ears often “pop” both on the way up and on the way down. How can you explain this effect? As you go up or down the atmospheric pressure changes and the popping is the inner ear adjusting to the pressure change – air flows out or in via the eustacean tubes (if they aren’t stopped up. ) Feb. 25 -29, 2008 Physics 214 Spring 2007 23

2 B-08 Buoyant Force Compare the Buoyant Force between two cylinders of equal volume and different mass. T Which object experiences the greater buoyant force, the heavier one or lighter one ? T FB Mg Scale reads tension in cord: T = Mg – FB Mg = FB + T Mg We find Fb to be exactly equal for both masses BUOYANT FORCE DOES NOT DEPEND ON THE MATERIAL OF THE OBJECT DISPLACING THE FLUID. THE BUOYANT FORCE DEPENDS ONLY ON THE VOLUME OF FLUID DISPLACED. Feb. 25 -29, 2008 Physics 214 Spring 2007 24

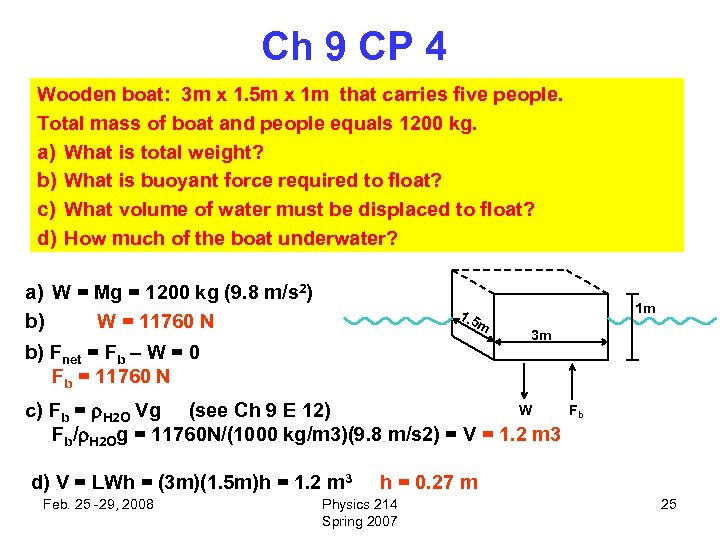Ch 9 CP 4 Wooden boat: 3 m x 1. 5 m x 1 m that carries five people. Total mass of boat and people equals 1200 kg. a) What is total weight? b) What is buoyant force required to float? c) What volume of water must be displaced to float? d) How much of the boat underwater? a) W = Mg = 1200 kg (9. 8 m/s 2) b) W = 11760 N 1. 5 m b) Fnet = Fb – W = 0 Fb = 11760 N 1 m 3 m W c) Fb = H 2 O Vg (see Ch 9 E 12) Fb/ H 2 Og = 11760 N/(1000 kg/m 3)(9. 8 m/s 2) = V = 1. 2 m 3 d) V = LWh = (3 m)(1. 5 m)h = 1. 2 m 3 Feb. 25 -29, 2008 Fb h = 0. 27 m Physics 214 Spring 2007 25

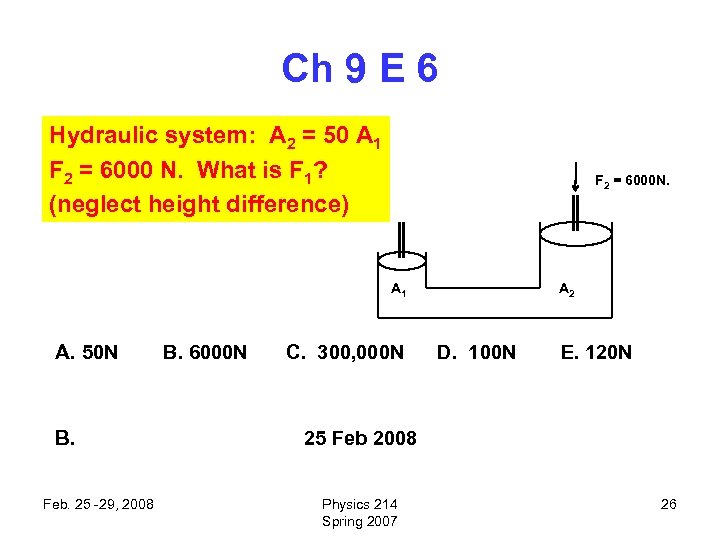Ch 9 E 6 Hydraulic system: A 2 = 50 A 1 F 2 = 6000 N. What is F 1? (neglect height difference) F 2 = 6000 N. A 1 A. 50 N B. Feb. 25 -29, 2008 B. 6000 N C. 300, 000 N A 2 D. 100 N E. 120 N 25 Feb 2008 Physics 214 Spring 2007 26

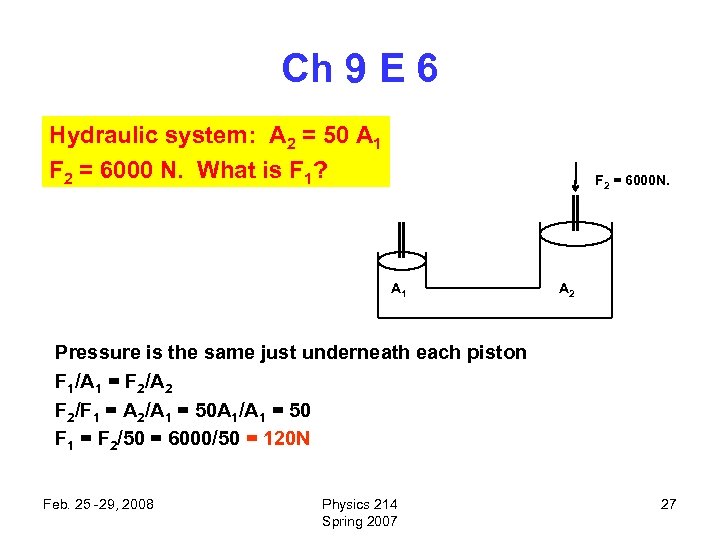Ch 9 E 6 Hydraulic system: A 2 = 50 A 1 F 2 = 6000 N. What is F 1? F 2 = 6000 N. A 1 A 2 Pressure is the same just underneath each piston F 1/A 1 = F 2/A 2 F 2/F 1 = A 2/A 1 = 50 A 1/A 1 = 50 F 1 = F 2/50 = 6000/50 = 120 N Feb. 25 -29, 2008 Physics 214 Spring 2007 27

Questions Chapter 9 Q 1 Is it possible for a 100 -lb woman to exert a greater pressure on the ground than a 250 -lb man? Explain. Yes. The pressure will be mg/A so if A is small e. g. small heels the pressure will be very large Q 3 The same force is applied to two cylinders that contain air. One has a piston with a large area, and the other has a piston with a small area. In which cylinder will the pressure be greater? The pressure is F/A so the one with the smallest A Feb. 25 -29, 2008 Physics 214 Spring 2007 28

Q 4 A penny and a quarter are embedded in the concrete bottom of a swimming pool filled with water. Which of these coins experiences the greater downward force due to water pressure acting on it? Each coin has to support the weight of water in a vertical column so the quarter has the biggest force F =PA Q 5 Why are bicycle tires often inflated to a higher pressure than automobile tires, even though the automobile tires must support a much larger weight? Once again the upward force has to support the weight so F = mg but F = PA where A is the area of the tire on the road so M/m = (PA)car/(Pa)bike so Ma/m. A = Pcar /Pbike the ratio of the areas is smaller than the ratio of the weights so Pbike is higher. Feb. 25 -29, 2008 Physics 214 Spring 2007 29

Q 6 The fluid in a hydraulic system pushes against two pistons, one with a large area and the other with a small area. A. Which piston experiences the greater force due to fluid pressure acting on it? B. When the smaller piston moves, does the larger piston move through the same distance, a greater distance, or a smaller distance than the smaller piston? A. The pressure is the same and F = PA so the larger piston has the larger force. B. The work done is the same so the small piston moves the most. Equivalently, to “conserve liquid volume” the smaller piston moves the larger distance. Q 8 When a mercury barometer is used to measure atmospheric pressure, does the closed end of the tube above the mercury column usually contain air? No it needs to be a vacuum Feb. 25 -29, 2008 Physics 214 Spring 2007 30

Q 9 Could we use water instead of mercury to make a barometer? What advantages and disadvantages would be associated with the use of water? The height of the liquid depends on the density. So one can use water but the column would be 33 feet high Q 10 If you climbed a mountain carrying a mercury barometer, would the level of the mercury column in the glass tube of the barometer increase or decrease (compared to the mercury reservoir) as you climb the mountain? The pressure decreases because you have a smaller column of air to support so the height would decrease Feb. 25 -29, 2008 Physics 214 Spring 2007 31

Q 15 Is it possible for a solid metal ball to float in mercury? The upward force is the weight of liquid displaced and the downward force is the weight of the ball. If the density of the liquid is greater than that of the ball it will float. Steel or copper will float, gold will sink (and amalgmate with the mercury, but that’s another story. ) Q 16 A rectangular metal block is suspended by a string in a breaker of water so that the block is completely surrounded by water. Is the water pressure at the bottom of the block equal to, greater than, or less than the water pressure at the top of the block? The pressure is ρgh so the pressure is higher at the bottom. The difference in pressure provides the upward force on the block Feb. 25 -29, 2008 Physics 214 Spring 2007 32

Q 19 A large bird lands on a rowboat that is floating in a swimming pool. Will the water level in the pool increase, decrease, or remain the same when the bird lands on the boat? The buoyant force is the weight of liquid displaced so to support a larger weight more liquid is displaced and the level rises Q 20 A rowboat is floating in a swimming pool when the anchor is dropped over the side. When the anchor is dropped, will the water level in the swimming pool increase, decrease, or remain the same? When the anchor is in the boat it’s whole weight is supported and the amount of water displaced balances that weight. When it is thrown overboard it sinks and only displaces it’s volume so the water level falls Feb. 25 -29, 2008 Physics 214 Spring 2007 33

Q 22 If an object has the same density as water, will the object float to the top, sink to the bottom, or take neither course? Providing the object and water are incompressible the object will stay at whatever depth it is placed. It will not sink or rise. Feb. 25 -29, 2008 Physics 214 Spring 2007 34

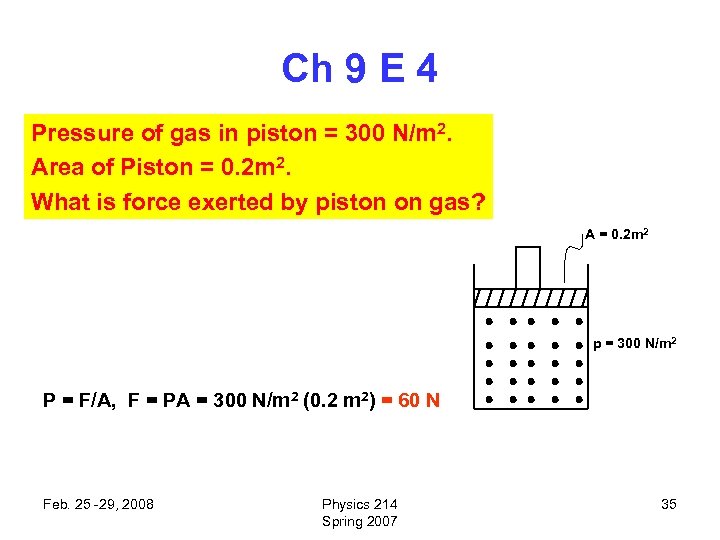Ch 9 E 4 Pressure of gas in piston = 300 N/m 2. Area of Piston = 0. 2 m 2. What is force exerted by piston on gas? A = 0. 2 m 2 p = 300 N/m 2 P = F/A, F = PA = 300 N/m 2 (0. 2 m 2) = 60 N Feb. 25 -29, 2008 Physics 214 Spring 2007 35

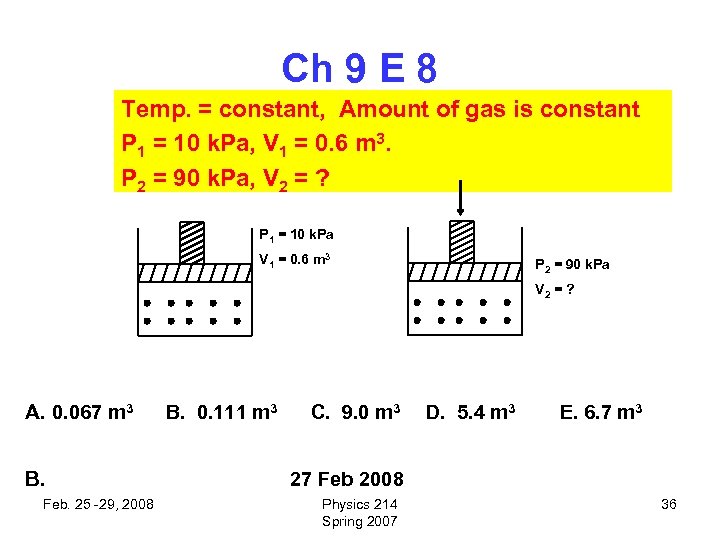Ch 9 E 8 Temp. = constant, Amount of gas is constant P 1 = 10 k. Pa, V 1 = 0. 6 m 3. P 2 = 90 k. Pa, V 2 = ? P 1 = 10 k. Pa V 1 = 0. 6 m 3 P 2 = 90 k. Pa V 2 = ? A. 0. 067 m 3 B. Feb. 25 -29, 2008 B. 0. 111 m 3 C. 9. 0 m 3 D. 5. 4 m 3 E. 6. 7 m 3 27 Feb 2008 Physics 214 Spring 2007 36

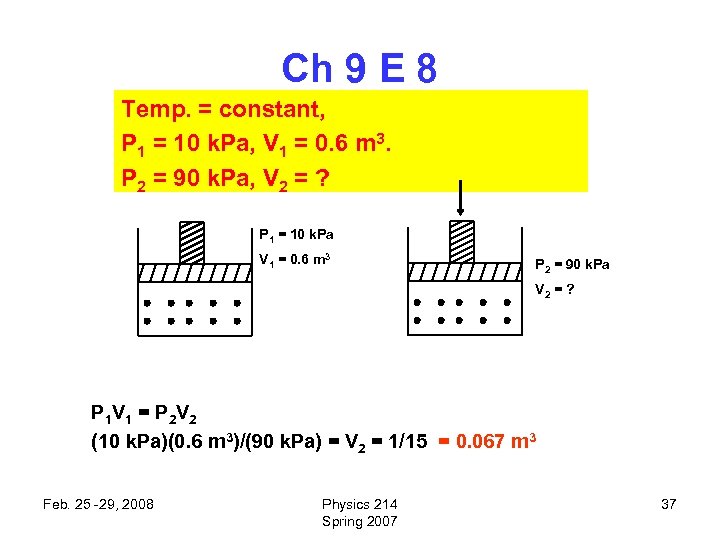Ch 9 E 8 Temp. = constant, P 1 = 10 k. Pa, V 1 = 0. 6 m 3. P 2 = 90 k. Pa, V 2 = ? P 1 = 10 k. Pa V 1 = 0. 6 m 3 P 2 = 90 k. Pa V 2 = ? P 1 V 1 = P 2 V 2 (10 k. Pa)(0. 6 m 3)/(90 k. Pa) = V 2 = 1/15 = 0. 067 m 3 Feb. 25 -29, 2008 Physics 214 Spring 2007 37

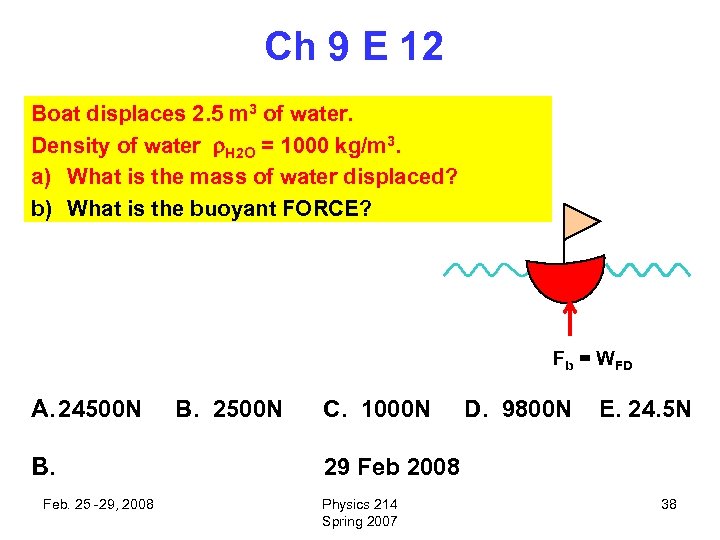Ch 9 E 12 Boat displaces 2. 5 m 3 of water. Density of water H 2 O = 1000 kg/m 3. a) What is the mass of water displaced? b) What is the buoyant FORCE? Fb = WFD A. 24500 N B. Feb. 25 -29, 2008 B. 2500 N C. 1000 N D. 9800 N E. 24. 5 N 29 Feb 2008 Physics 214 Spring 2007 38

Ch 9 E 12 Boat displaces 2. 5 m 3 of water. Density of water H 2 O = 1000 kg/m 3. a) What is the mass of water displaced? b) What is the buoyant force? a) Mass of fluid displaced b) (m. FD) = volume x density of fluid. c) MFD = VFD H 2 O = (2. 5 m 3)(1000 kg/m 3) = 2500 Fb = WFD kg b) Buoyant force equals weight of fluid displaced. c) Fb = WFD = m. FD g = (2500 kg)(9. 8 m/s 2) = 24500 N Feb. 25 -29, 2008 Physics 214 Spring 2007 39

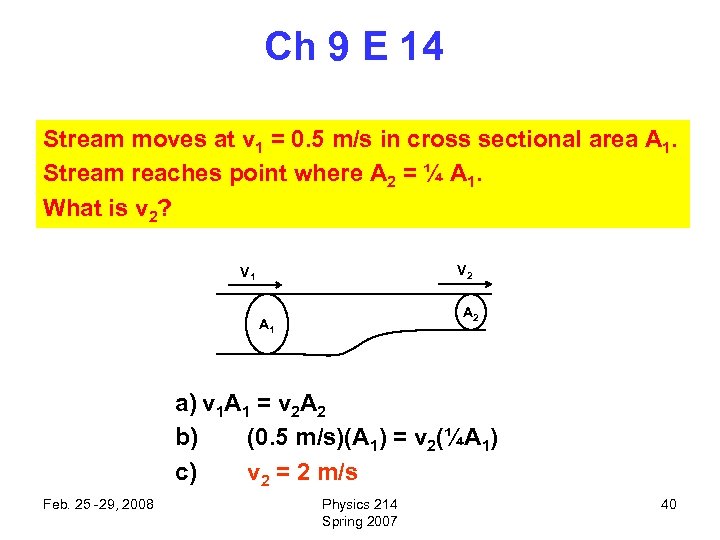Ch 9 E 14 Stream moves at v 1 = 0. 5 m/s in cross sectional area A 1. Stream reaches point where A 2 = ¼ A 1. What is v 2? V 2 V 1 A 2 A 1 a) v 1 A 1 = v 2 A 2 b) (0. 5 m/s)(A 1) = v 2(¼A 1) c) v 2 = 2 m/s Feb. 25 -29, 2008 Physics 214 Spring 2007 40

Ch 9 CP 2 Water density = H 2 O = 1000 kg/m 3. Depth of swimming pool = 3 m. a) What is the volume of a column of water 3 m deep and cross sectional area 0. 5 m 2? b) What is its mass? c) What is its weight? d) What is the excess pressure exerted on the pool bottom? e) Compare to atmospheric pressure. a) V = Ad = (0. 5 m 2)(3 m) = 1. 5 m 3 b) M = V = (1. 5 m 3)(1000 kg/m 3) = 1500 kg c) W = Mg = (1500 kg)(9. 8 m/s 2) = 14700 N 0. 5 m 2 3 m d) P = F/A = 14700 N/0. 5 m 2 = 29400 Pa e) Atmospheric Pressure is about 100 k. Pa f) P is about 30 k. Pa g) P/Atm = (29400 Pa)/(1. 013 x 105 Pa) = 0. 29 Feb. 25 -29, 2008 Physics 214 Spring 2007 41

Balloons FB mg Feb. 25 -29, 2008 Any object in the atmosphere is subject to a buoyant force and Archimedes law applies so if the buoyant force is greater than the weight of an object it will rise. So since the material of a balloon has a density greater than air then the balloon must be filled with a gas having a density less than air. In practice balloons either use Helium or hot air. As the balloon rises the buoyant force decreases and the balloon will float at constant altitude when the buoyant force is equal to the weight. Physics 214 Spring 2007 42

Surface tension The molecules and atoms in a liquid are continually in motion so that a molecule at the surface can escape and this is evaporation. However a molecule at the surface feels an attractive force pulling it back into the liquid and this is surface tension. This is the reason that one can form bubbles and water drops The capiilary action is caused by “wetting” forces between the edge of the liquid surface and the walls of the tube. Feb. 25 -29, 2008 Physics 214 Spring 2007 43

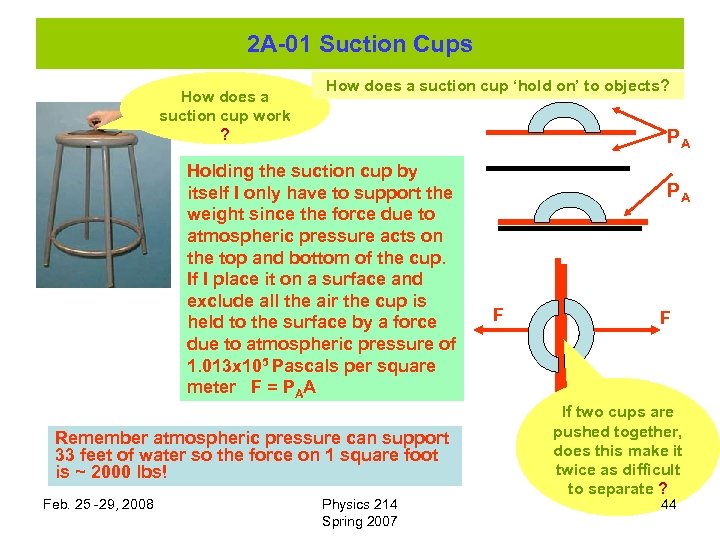2 A-01 Suction Cups How does a suction cup work ? How does a suction cup ‘hold on’ to objects? PA Holding the suction cup by itself I only have to support the weight since the force due to atmospheric pressure acts on the top and bottom of the cup. If I place it on a surface and exclude all the air the cup is held to the surface by a force due to atmospheric pressure of 1. 013 x 105 Pascals per square meter F = PAA Remember atmospheric pressure can support 33 feet of water so the force on 1 square foot is ~ 2000 lbs! Feb. 25 -29, 2008 Physics 214 Spring 2007 PA F F If two cups are pushed together, does this make it twice as difficult to separate ? 44

Otto von Guericke 1602 - 1686 was the “inventor” of the nothing we now call a vacuum. Von Guericke created a vacuum by attaching two hemispheres and then evacuating the air from the resultant sphere. Von Guericke demonstrated the force of the vacuum before the German emperor Ferdinand III by having two teams of horses attempt to disengage the hemispheres. Feb. 25 -29, 2008 Physics 214 Spring 2007 45

2 B-05 Pressure Forces in Liquids An open ended cylinder kept shut by liquid pressure What happens as the submerged cylinder filled with air is filled with water ? There are two forces acting on the plate. It’s weight down and PA up. When PA exceeds the weight the cylinder stays intact In this situation the plate has to now support the weight of the water and when the weight of the water plus plate exceeds PA the cylinder opens Air PA Water PA THE LIQUID PRESSURE DEPENDS ONLY ON DEPTH P = ρgh. THE UPWARD FORCE DEPENDS ON THE AREA F = PA Feb. 25 -29, 2008 Physics 214 Spring 2007 46

2 B-04 Liquid Pressure Investigating Pressure in different directions within a liquid in equilibrium. What will happen to the reading on the manometer as the sensor is rotated ? PRESSURE IS NOT A VECTOR. IT ACTS EQUALLY IN ALL DIRECTIONS g A B The increase in pressure ρgh is measured by the difference in height of the liquid in the U tube. h A B IF A LIQUID IS IN EQUILIBRIUM, THE FORCES ACTING AT A POINT CANNOT HAVE A PREFERENTIAL DIRECTION OR THE LIQUID WOULD MOVE. AT ANY GIVEN POINT IN A STATIONARY LIQUID, THE PRESSURE IS THE SAME IN ALL DIRECTIONS. Feb. 25 -29, 2008 Physics 214 Spring 2007 47

2 B-09 Archimedes I T What happens to the reading on the upper scale when the block is lowered into the beaker of water ? FB Mg Should anything happen to the reading on the lower scale ? The fluid exerts a buoyant force on the block, which reduces the tension on the cord. The reading on the scale is lowered. T = Mg – FB Since the fluid exerts a force on the block, the block exerts an EQUAL and OPPOSITE force on the fluid. EVEN THOUGH THE BLOCK DOES NOT ‘TOUCH’ THE LOWER SCALE, THE FORCE ON THE FLUID DUE TO THE BLOCK IS TRANSMITTED TO THE SCALE. THE REDUCTION IN READING ON THE UPPER SCALE IS EXACTLY EQUAL TO THE INCREASE IN READING ON THE LOWER SCALE. IF THE CONTAINER WAS FULL SO THAT WHEN THE BLOCK WAS INSERTED THE VOLUME THE BLOCK DISPLACED SPILLS OUT OF THE CONTAINER THEN THE BOTTOM SCALE WOULD NOT CHANGE. Feb. 25 -29, 2008 Physics 214 Spring 2007 48

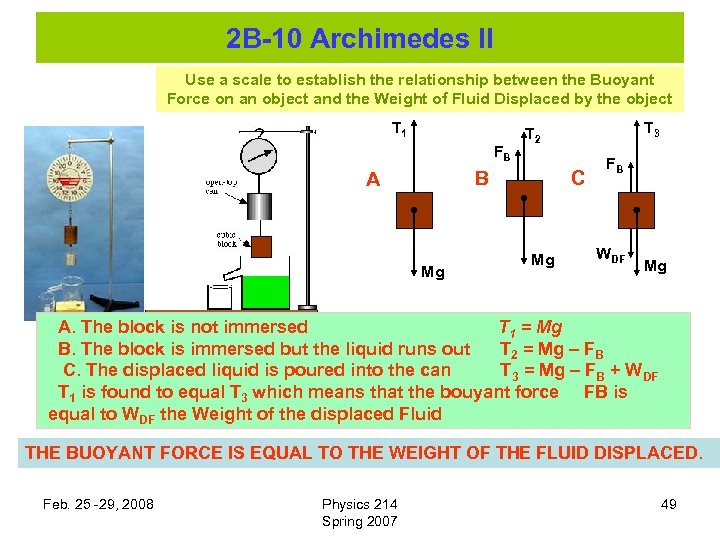2 B-10 Archimedes II Use a scale to establish the relationship between the Buoyant Force on an object and the Weight of Fluid Displaced by the object T 1 FB B A Mg T 3 T 2 C Mg FB WDF Mg A. The block is not immersed T 1 = Mg B. The block is immersed but the liquid runs out T 2 = Mg – FB C. The displaced liquid is poured into the can T 3 = Mg – FB + WDF T 1 is found to equal T 3 which means that the bouyant force FB is equal to WDF the Weight of the displaced Fluid THE BUOYANT FORCE IS EQUAL TO THE WEIGHT OF THE FLUID DISPLACED. Feb. 25 -29, 2008 Physics 214 Spring 2007 49