a2134294c0eecd575e5ce2a53083d149.ppt
- Количество слайдов: 44

Liquid flows on surfaces: the boundary condition E. CHARLAIX University of Lyon, France NANOFLUIDICS SUMMER SCHOOL August 20 -24 2007 THE ABDUS SALAM INTERNATIONAL CENTER FOR THEORETICAL PHYSICS

The no-slip boundary condition (bc): a long lasting empiricism regularly questionned Some examples of importance of the b. c. in nanofluidics Pressure drop in nanochannels Elektrokinetics effects Dispersion & mixing Theory of the h. b. c. for simple liquids Slippage effects in macroscopic flows ?

Microchannels… …nanochannels 500 nm Miniaturization increases surface to volume ratio: importance of surface phenomena The description of flows requires constitutive equation (bulk property of fluid) + boundary condition (surface property) Yesterday we saw that N. S. equation for simple liquids is very robust constitutive equation down to (some) molecular scale. What about boundary condition ?
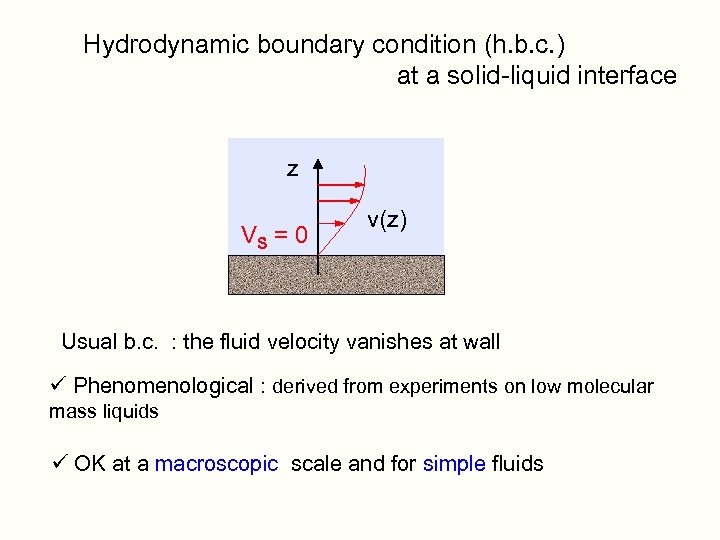
Hydrodynamic boundary condition (h. b. c. ) at a solid-liquid interface z VS = 0 v(z) Usual b. c. : the fluid velocity vanishes at wall ü Phenomenological : derived from experiments on low molecular mass liquids ü OK at a macroscopic scale and for simple fluids

The nature of hydrodynamics bc’s has been widely debated in 19 th century Goldstein S. 1969. Fluid mechanics in the first half of this century. Annu. Rev. Fluid Mech 1: 1– 28 Lauga & al, in Handbook of Experimental Fluid Dynamics, 2005 M. Denn, 2001 Annu. Rev. Fluid Mech. 33: 265– 87 Batchelor, An introduction to fluid dynamics, 1967 Goldstein 1938

But wall slippage occurs in polymer flows… Shark-skin effect in extrusion of polymer melts Pudjijanto & Denn 1994 J. Rheol. 38: 1735 … and some time suspected on non-wetting surfaces And also Bulkley (1931), Chen & Emrich (1963), Debye & Cleland (1958)…
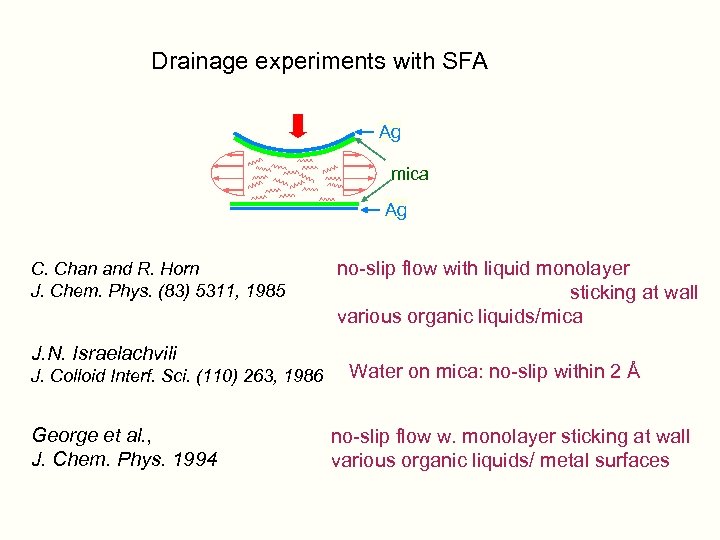
Drainage experiments with SFA Ag mica Ag C. Chan and R. Horn J. Chem. Phys. (83) 5311, 1985 J. N. Israelachvili J. Colloid Interf. Sci. (110) 263, 1986 George et al. , J. Chem. Phys. 1994 no-slip flow with liquid monolayer sticking at wall various organic liquids/mica Water on mica: no-slip within 2 Å no-slip flow w. monolayer sticking at wall various organic liquids/ metal surfaces

N. V. Churaev, V. D; Sobolev and A. NSomov J. Colloid Interf. Sci. (97) 574, 1984 Water slips in hydrophobic capillaries slip length 70 nm

Partial slip and solid-liquid friction z b Navier 1823 Maxwell 1856 v(z) VS ≠ 0 Tangentiel stress at interface VS : slip velocity s. S : tangential stress at the solid surface h : liquid viscosity l : liquid-solid friction coefficient b : slip length ∂V = g : shear rate ∂z
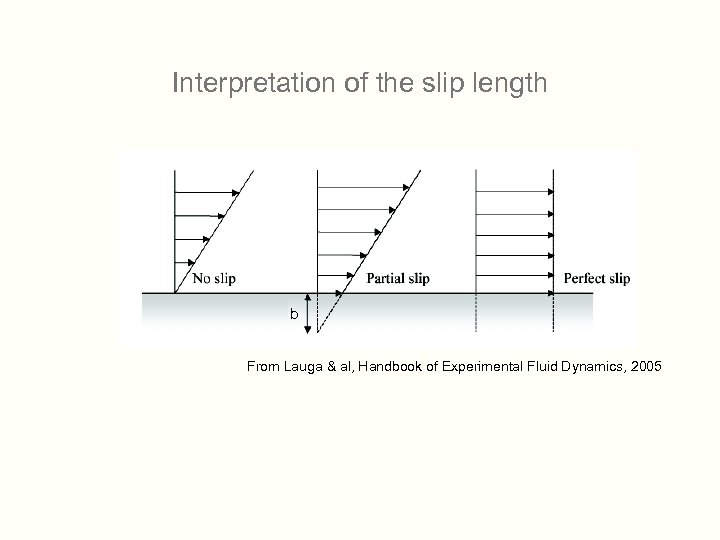
Interpretation of the slip length b From Lauga & al, Handbook of Experimental Fluid Dynamics, 2005

Some properties of the slip length n No-slip bc (b=0) is associated to very large liquid-solid friction n The bc is an interface property. The slip length has not to be related to an internal scale in the fluid On a mathematically smooth surface, b=∞ (perfect slip). n The hydrodynamic b. c. is fully characterized by b(g) n The hydrodynamic bc is linear if the slip length does not depend on the shear rate.

The no-slip boundary condition (bc): a long lasting empiricism regularly questionned Some examples of importance of the b. c. in nanofluidics Pressure drop in nanochannels Elektrokinetics effects Dispersion & mixing Theory of the h. b. c. for simple liquids Slippage effects in macroscopic flows ?
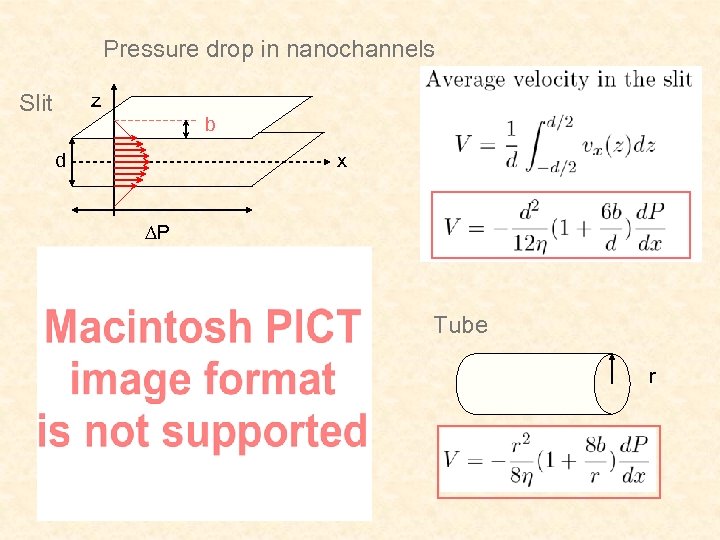
Pressure drop in nanochannels z Slit b d x ∆P Tube r

Exemple 1 slit d=1 µm Exemple 2 r = 2 nm tube %error on permeability : 12% b=20 nm Error factor on permeability : 80 (2 order of magnitude)
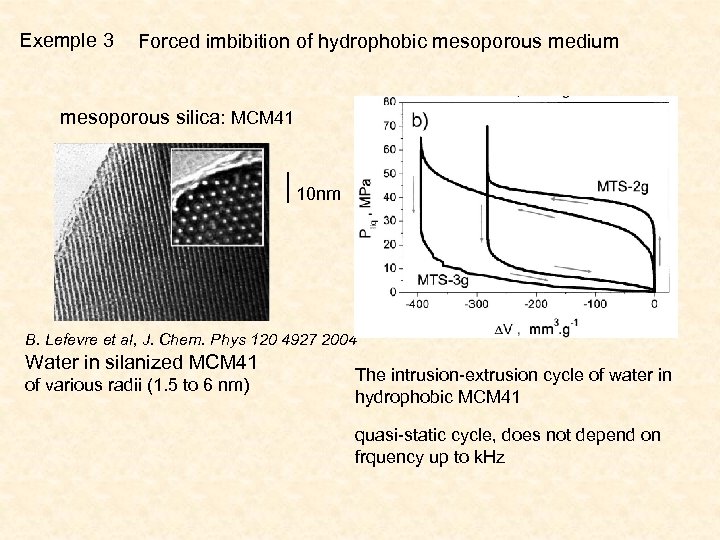
Exemple 3 Forced imbibition of hydrophobic mesoporous medium mesoporous silica: MCM 41 10 nm B. Lefevre et al, J. Chem. Phys 120 4927 2004 Water in silanized MCM 41 of various radii (1. 5 to 6 nm) The intrusion-extrusion cycle of water in hydrophobic MCM 41 quasi-static cycle, does not depend on frquency up to k. Hz
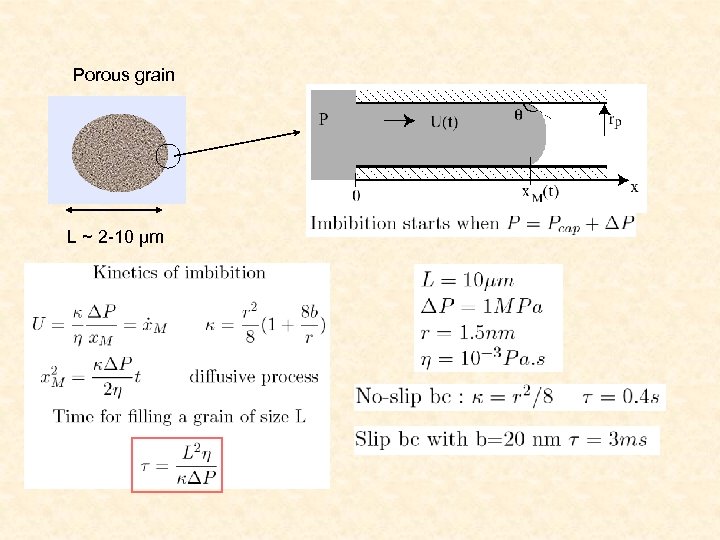
Porous grain L ~ 2 -10 µm

Dispersion of transported species - Mixing d Taylor dispersion t=0 injection time t Without molecular diffusion: Molecular diffusion spreads the solute through the width within Solute motion is analogous to random walk:
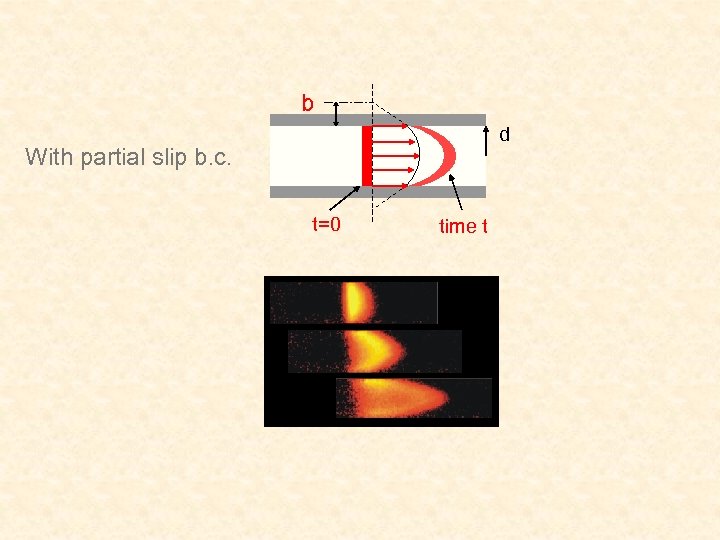
b d With partial slip b. c. t=0 time t
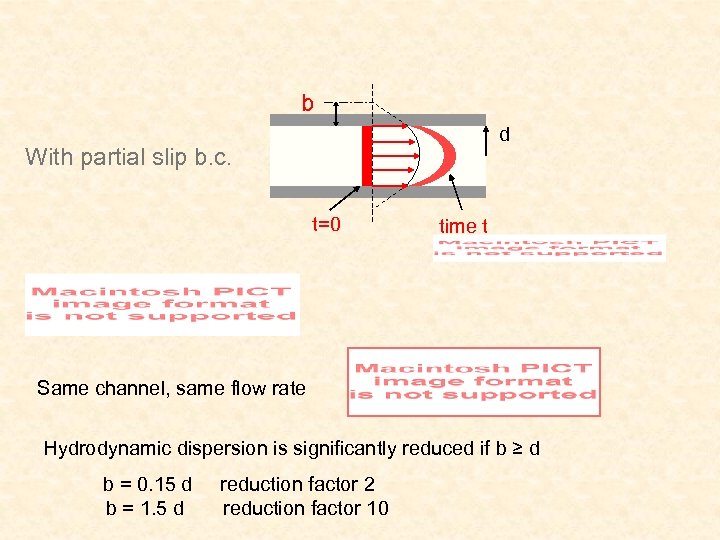
b d With partial slip b. c. t=0 time t Same channel, same flow rate Hydrodynamic dispersion is significantly reduced if b ≥ d b = 0. 15 d reduction factor 2 b = 1. 5 d reduction factor 10
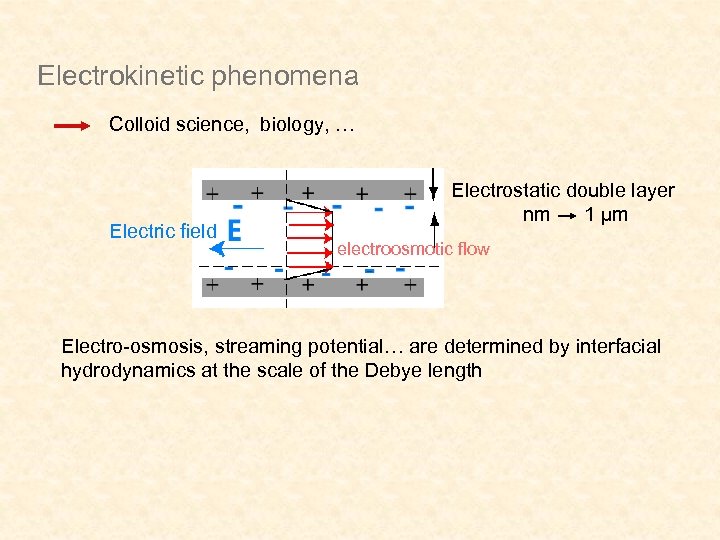
Electrokinetic phenomena Colloid science, biology, … Electric field Electrostatic double layer nm 1 µm electroosmotic flow Electro-osmosis, streaming potential… are determined by interfacial hydrodynamics at the scale of the Debye length

z vos E + + + + + - - - x
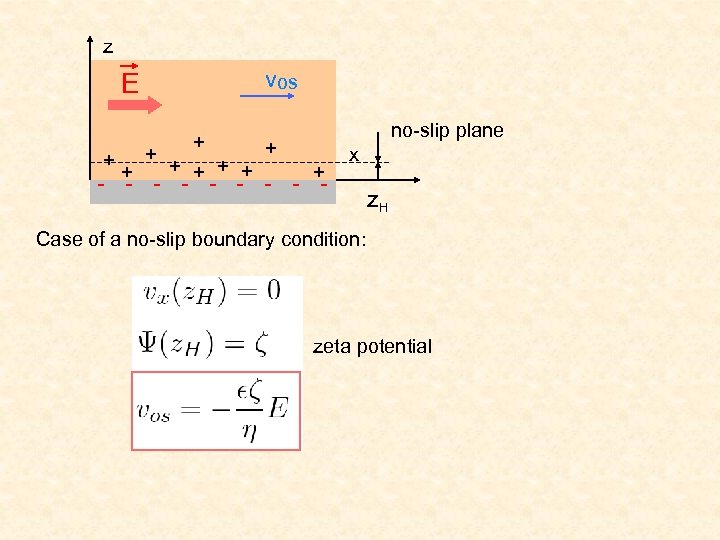
z E vos + + + + + no-slip plane + x - - - z. H Case of a no-slip boundary condition: zeta potential

z vos E + + + + + x - - Case of a partial slip boundary condition:

Ø At constant Ys the electroosmotic velocity depends on Debye length. Pb for measuring surface charges Ø Possibility of very large el-osmotic flow by decreasing k-1 ? Example: b=20 nm k-1 = 3 nm at 10 -2 M nos increased by 800% Churaev et al, Adv. Colloid Interface Sci. 2002 L. Joly et al, Phys. Rev. Lett, 2004

The no-slip boundary condition (bc): a long lasting empiricism regularly questionned Some examples of importance of the b. c. in nanofluidics Pressure drop in nanochannels Elektrokinetics effects Dispersion & mixing Theory of the h. b. c. for simple liquids What about macroscopic flows ?
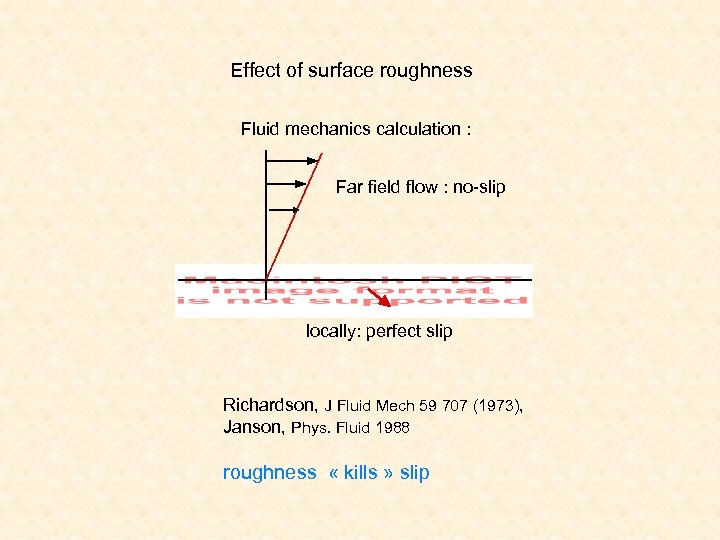
Effect of surface roughness Fluid mechanics calculation : Far field flow : no-slip locally: perfect slip Richardson, J Fluid Mech 59 707 (1973), Janson, Phys. Fluid 1988 roughness « kills » slip
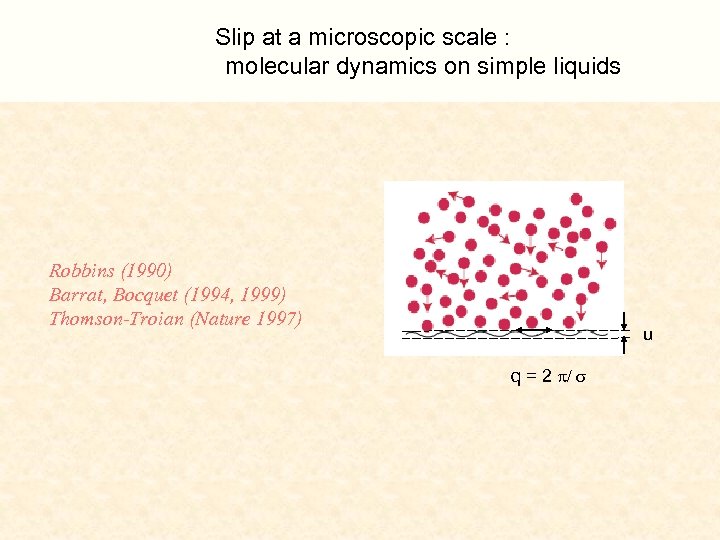
Slip at a microscopic scale : molecular dynamics on simple liquids Robbins (1990) Barrat, Bocquet (1994, 1999) Thomson-Troian (Nature 1997) u q = 2 p/ s

Thermodynamic equilibrium determination of b. c. with Molecular Dynamics simulations Bocquet & Barrat, Phys Rev E 49 3079 (1994) Be j(r, t) the fluctuating momentum density at point r Assume that it obeys Navier-Stokes equation And assume boundary condition b

Then take its <x, y> average And auto-correlation function C(z, z’, t) obeys a diffusion equation with boundary condition b and initial value given by thermal equilibrium 2 D density C(z, z’, t) can be solved analytically and obtained as a function of b b can be determined by ajusting analytical solution to data measured in equilibrium Molecular Dynamics simulation
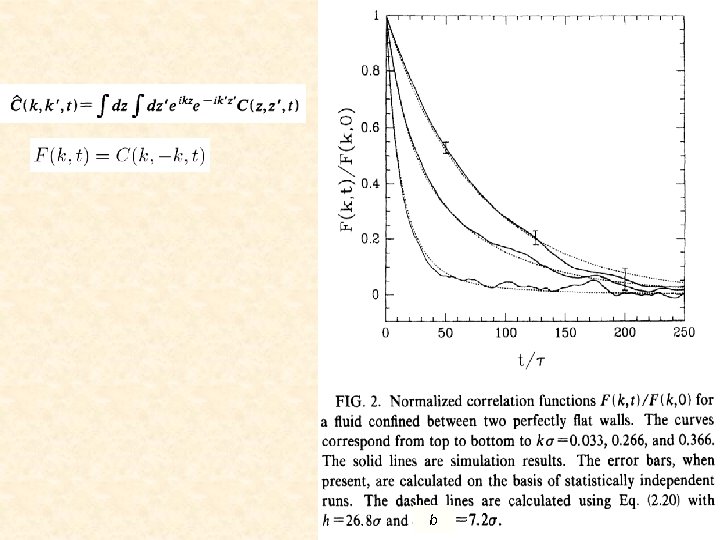
b
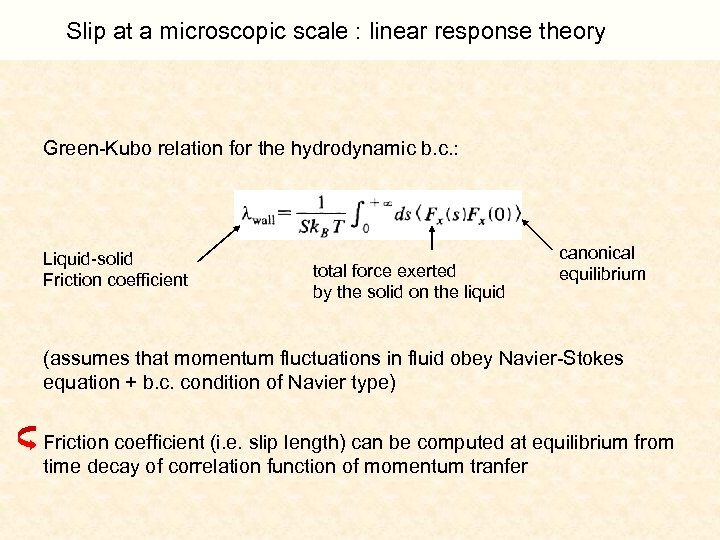
Slip at a microscopic scale : linear response theory Green-Kubo relation for the hydrodynamic b. c. : Liquid-solid Friction coefficient total force exerted by the solid on the liquid canonical equilibrium (assumes that momentum fluctuations in fluid obey Navier-Stokes equation + b. c. condition of Navier type) Friction coefficient (i. e. slip length) can be computed at equilibrium from time decay of correlation function of momentum tranfer
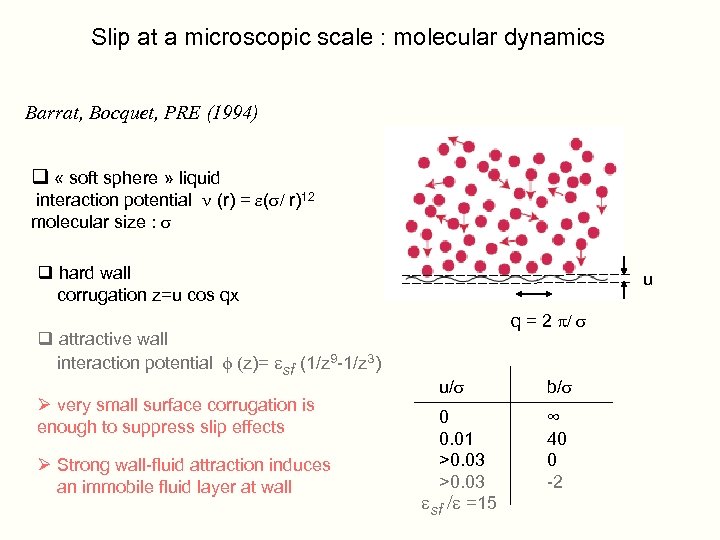
Slip at a microscopic scale : molecular dynamics Barrat, Bocquet, PRE (1994) q « soft sphere » liquid interaction potential n (r) = e(s/ r)12 molecular size : s q hard wall corrugation z=u cos qx q attractive wall interaction potential f (z)= esf (1/z 9 -1/z 3) Ø very small surface corrugation is enough to suppress slip effects Ø Strong wall-fluid attraction induces an immobile fluid layer at wall u q = 2 p/ s u/s 0 0. 01 >0. 03 esf /e =15 b/s ∞ 40 0 -2
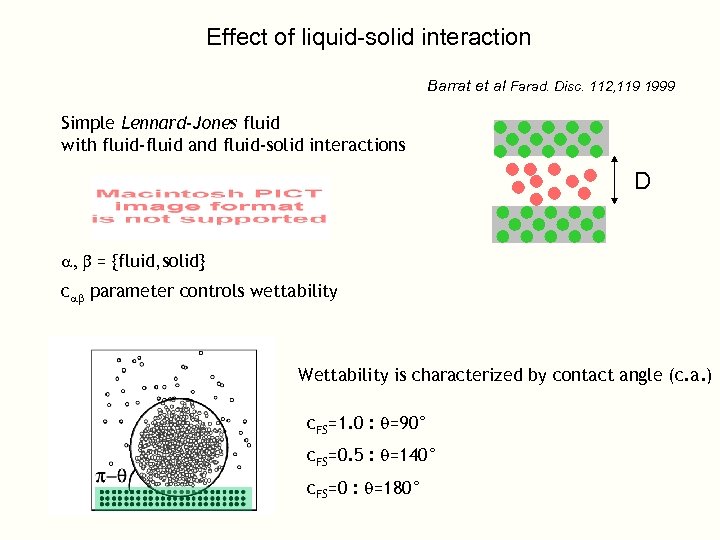
Effect of liquid-solid interaction Barrat et al Farad. Disc. 112, 119 1999 Simple Lennard-Jones fluid with fluid-fluid and fluid-solid interactions D a, b = {fluid, solid} cab parameter controls wettability Wettability is characterized by contact angle (c. a. ) c. FS=1. 0 : q=90° c. FS=0. 5 : q=140° c. FS=0 : q=180°
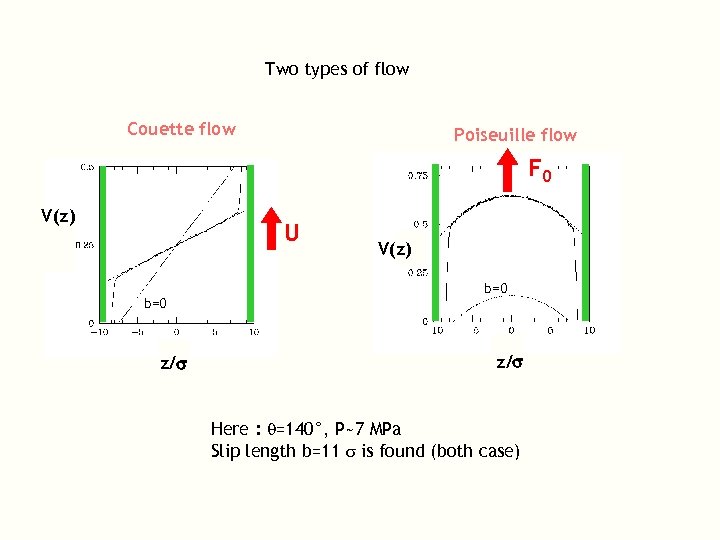
Two types of flow Couette flow Poiseuille flow F 0 V(z) U b=0 z/s V(z) b=0 z/s Here : q=140°, P~7 MPa Slip length b=11 s is found (both case)
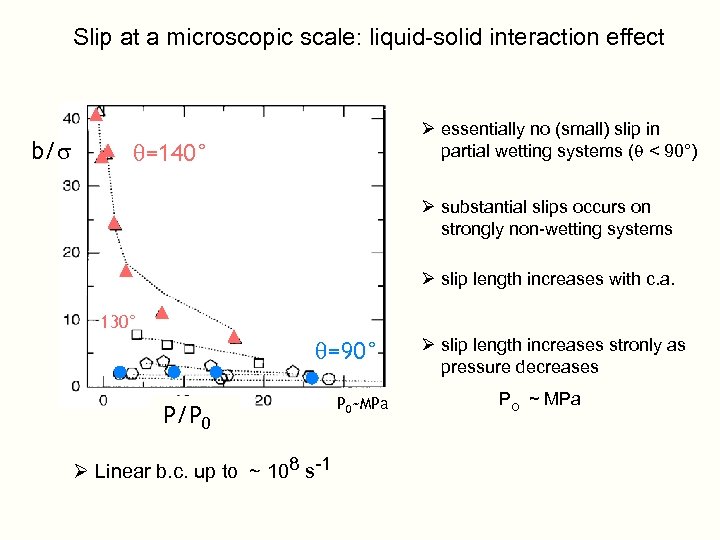
Slip at a microscopic scale: liquid-solid interaction effect b/s Ø essentially no (small) slip in partial wetting systems (q < 90°) q=140° Ø substantial slips occurs on strongly non-wetting systems Ø slip length increases with c. a. 130° q=90° P/P 0 Ø Linear b. c. up to ~ 108 s-1 P 0~MPa Ø slip length increases stronly as pressure decreases Po ~ MPa

fluid density profile across the cell Soft spheres on hard repulsive wall Lennard-Jones fluid q = 137° Slip increases with reduced fluid density at wall. However slippage does not reduce to « air cushion » at wall.
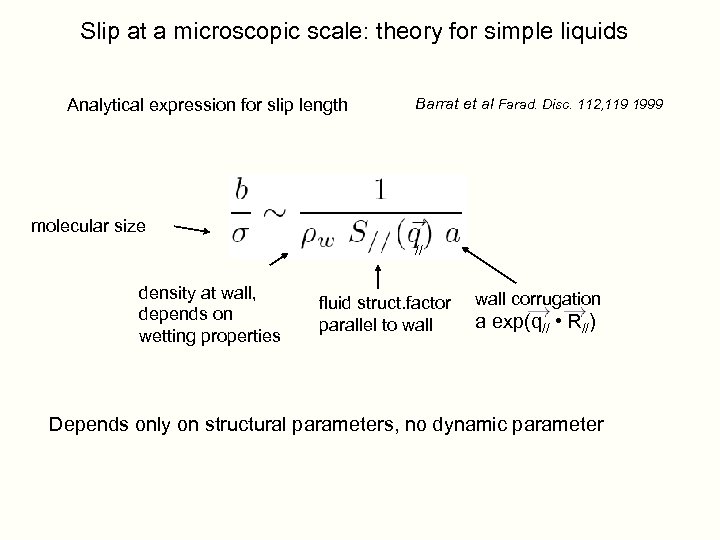
Slip at a microscopic scale: theory for simple liquids Analytical expression for slip length Barrat et al Farad. Disc. 112, 119 1999 molecular size // density at wall, depends on wetting properties fluid struct. factor parallel to wall corrugation a exp(q// • R//) Depends only on structural parameters, no dynamic parameter

Intrinsic b. c. on smooth surfaces : conclusion. Ø at moderate shear rate (g < 108 s-1 ) essentially no slip in wetting systems Ø substantial slips occurs in strongly non-wetting systems slip length increases with c. a. slip length depends strongly on pressure Ø slip length amplitude is moderate (~ 5 nm at q ~ 120° ) Ø slip length is not expected to depend on fluid viscosity (≠ polymers) Ø non-linear slip develops above a (high) critical shear rate (~ 109 s-1 ) Thomson-Troian Nature 1997

The no-slip boundary condition (bc): a long lasting empiricism regularly questionned Some examples of importance of the b. c. in nanofluidics Pressure drop in nanochannels Elektrokinetics effects Dispersion & mixing Theory of the h. b. c. for simple liquids Slippage effects in macroscopic flows ?

Duez, Ybert, Clanet, Bocquet Nature Physics 3, 180, 2007
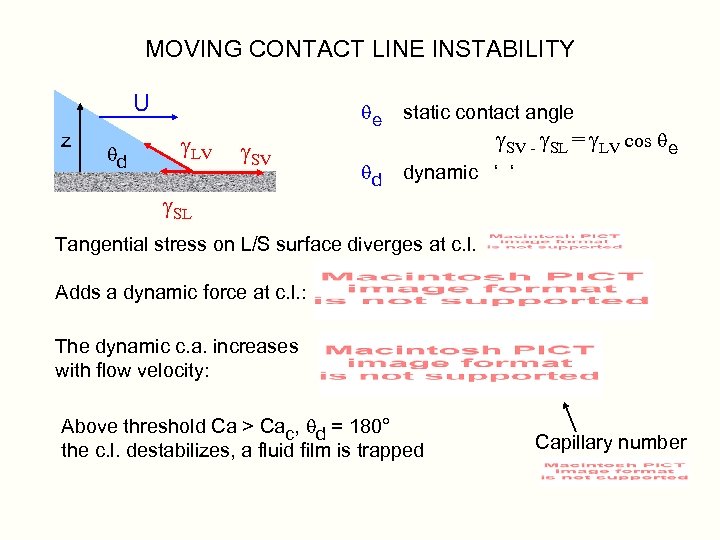
MOVING CONTACT LINE INSTABILITY U z qd g. LV qe g. SV g. SL static contact angle qd dynamic ‘ ‘ g. SV - g. SL = g. LV cos qe Tangential stress on L/S surface diverges at c. l. Adds a dynamic force at c. l. : The dynamic c. a. increases with flow velocity: Above threshold Ca > Cac, qd = 180° the c. l. destabilizes, a fluid film is trapped Capillary number
LANDAU-LEVITCH EFFECT U De Gennes, Brochart et Quéré, Gouttes bulles perles et ondes, 2005

ANTI LANDAU-LEVITCH EFFECT U Duez & al Nature Physics 3, 180, 2007

Duez & al Nature Physics 3, 180, 2007
a2134294c0eecd575e5ce2a53083d149.ppt