Линейные пространства и операторы Пушникова Марина Юрьевна

Линейные пространства и операторы Пушникова Марина Юрьевна

Определение вектора N-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде =(х1, х2, …, хn), где xi – i-я компонента вектора Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты

Действия над векторами § Суммой двух векторов одинаковой размерности n называется вектор, компоненты которого равны сумме соответствующих компонент слагаемых векторов § Произведением вектора на действительное число называется вектор, компоненты которого равны произведению этого числа на соответствующие компоненты вектора

1. 2. 3. 4. 5. 6. 7. 8. Свойства действий над векторами Переместительное свойство суммы Сочетательное свойство относительно числового множителя Распределительное свойство суммы числовых множителей Существование нулевого вектора Существование противоположного вектора Существование единицы

Определения векторного и линейного пространства § Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие 8 аксиомам, называется векторным пространством § Линейное пространство – это множество элементов, в котором определены операции сложения и умножения на число, удовлетворяющие 8 аксиомам

Линейная зависимость и линейная независимость векторов § Вектор называется линейной комбинацией векторов , если он равен сумме произведений этих векторов на произвольные действительные числа , т. е. § Векторы называются линейно зависимыми, если существуют такие числа , не равные одновременно нулю, что. В противном случае эти векторы называются линейно независимыми

Свойства линейно зависимых векторов § Векторы линейно зависимы тогда и только тогда, когда по крайней мере один из них линейно выражается через остальные § Если среди векторов имеется нулевой вектор, то эти векторы линейно зависимы § Если часть векторов являются линейно зависимыми, то и все эти векторы – линейно зависимые

Пример: являются ли векторы линейно зависимыми? Ответ: векторы линейно зависимы

Размерность пространства § Линейное пространство R называется nмерным, если в нем существуют nлинейно независимых векторов, а любые из (n+1) векторов уже являются зависимыми § Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов § Обозначается dim. R=n

Базис линейного пространства § Базисом линейного пространства R называется совокупность линейно независимых векторов n–мерного пространства R § Любой вектор линейного пространства R можно представить и притом единственным образом в виде линейной комбинации векторов базиса § разложение вектора по базису , а числа координаты вектора относительно этого базиса

Пример: доказать, что векторы образуют базис Ответ: векторы образуют базис

Переход к новому базису Пусть R, а - старый базис в пространстве - новый базис, т. е. Между координатами вектора относительно нового и старого базиса существует следующая взаимосвязь:

Пример: в базисе векторы Вектор , заданный в базисе выразить в базисе заданы. ,

Ответ:

Скалярное произведение Скалярным произведением двух nмерных векторов называется число, равное сумме произведений соответствующих координат Свойства: 1. Переместительное 2. Распределительное относительно сложения 3. Распределительное относительно умножения на число 4. Скалярный квадрат вектора является неотрицательным числом

Евклидовое пространство Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее 4 свойствам (аксиомам), называется евклидовым Экономический смысл скалярного произведения: Скалярное произведение вектора объема различных товаров на вектор их цен выражает суммарную стоимость этих товаров

Длина (норма) вектора Длиной (нормой) вектора в евклидовом пространстве называется число, равное квадратному корню из скалярного квадрата вектора Свойства длины вектора: 1. Норма нулевого вектора равна нулю 2. Норма вектора, умноженного на число, равна произведению модуля этого числа на норму самого вектора 3. Неравенство Коши - Буняковского 4. Неравенство треугольника

Углы и перпендикулярность § Угол между векторами равен скалярному произведению этих векторов, разделенному на произведение норм этих векторов § Два вектора ортогональны, если их скалярное произведение равно нулю § Векторы n-мерного евклидова пространства образуют ортонормированный базис, если эти векторы попарно ортогональны и норма каждого равна единице § В любом n-мерном евклидовом пространстве существует ортонормированный базис

Линейный оператор § Оператором, действующим из одного линейного пространства в другое, называется закон при котором каждому вектору из первого пространства ставится в соответствие единственный вектор из другого пространства, при этом первый вектор называется прообразом второго вектора, а второй – образом первого § Оператор называется линейным, если выполняются § свойство аддитивности § свойство однородности

Матрица линейного оператора Каждому линейному оператору соответствует матрица в данном базисе и обратно, любой матрице n-го порядка соответствует линейный оператор n-мерного пространства - где А – матрица линейного оператора, прообраз вектора , - образ вектора

Пример: найти образ вектора если матрица оператора имеет вид

Действия над линейными операторами 1. Сумма двух линейных операторов 2. Произведение линейного оператора на число 3. Произведение линейных операторов

Классификация линейных операторов § Нулевой оператор – это оператор, который переводит все векторы линейного пространства в нулевые § Тождественный оператор – это оператор, который оставляет все векторы линейного пространства без изменения

Зависимость между матрицами одного оператора в разных базисах Матрицы А и А* линейного оператора А(х) в базисах связаны соотношением , где С – матрица перехода от старого базиса к новому

Пример: в двумерном базисе оператор имеет матрицу в новом базисе . Найти матрицу этого оператора

Собственный вектор и собственное значение Ненулевой вектор называется собственным вектором оператора А, если существует такое число λ, что при этом число λ называется собственным значением оператора А соответствующим вектору уравнение называется характеристическим уравнением оператора А, а определитель – характеристическим многочленом оператора А

Пример: найти собственные векторы и собственные значения оператора А, заданного матрицей Ответ: при λ= -5 собственный вектор при λ=7 собственный вектор где t – любое число

Самая простая матрица линейного оператора § Матрица линейного оператора А в базисе, состоящем из его собственных векторов, является диагональной § Если матрица линейного оператора А в некотором базисе является диагональной, то все векторы этого базиса собственные § Если линейный оператор имеет n попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид

Пример: привести матрицу к диагональному виду

Квадратичная форма Квадратичной формой от n переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом причем

Пример: записать квадратичную форму в матричном виде

Свойства квадратичных форм § При невырожденном линейном преобразовании X=CY матрица квадратичной формы принимает вид A*=CTAC § Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду § Число слагаемых с положительными (отрицательными) коэффициентами не зависит от способа приведения формы к этому виду § Ранг матрицы квадратичной формы равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях

Пример: Дана квадратичная форма L(x 1, x 2)=2 x 12+4 x 1 x 2 -3 x 22. Найти квадратичную форму L(y 1, y 2), полученную из данной линейным преобразованием x 1=2 y 1 -3 y 2, x 2=y 1+y 2

Пример: привести к каноническому виду квадратичную форму

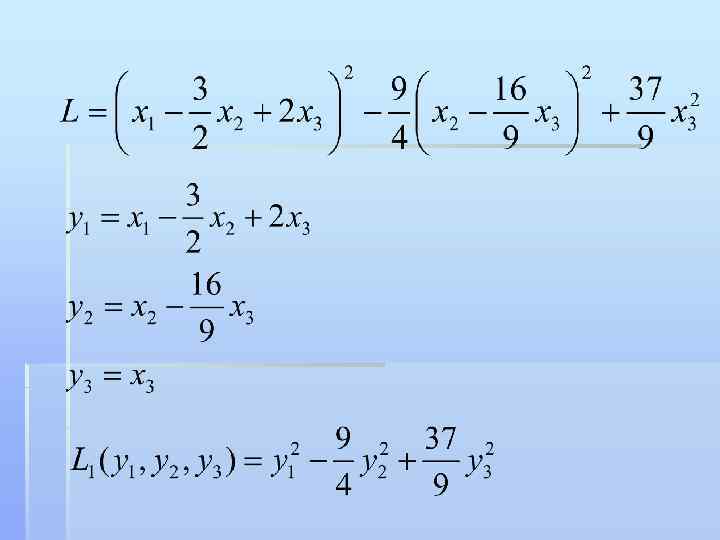
Положительно определенные квадратичные формы § Квадратичная форма называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля, она положительна (отрицательна) § Для того чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения матрицы были положительны (отрицательны) § Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры этой матрицы были положительны (для отрицательно определенных квадратичных форм главные миноры чередуют свои знаки, начиная с минуса)

Пример: Доказать, что квадратичная форма является положительно определенной

Пример: Доказать, что квадратичная форма является положительно определенной