Линейные преобразования графика функции 1 курс 1 семестр Автор Календарева Н. Е. © 2011 г.
План 1. 2. 3. 4. 5. 6. 7. 8. Перенос вдоль оси Ох Перенос вдоль оси Оу Сжатие (растяжение) вдоль оси Ох Сжатие (растяжение) вдоль оси Оу Симметрия относительно оси Ох Симметрия относительно оси Оу Примеры Домашнее задание
Линейные преобразования графика функции К линейным преобразованиям графика функции относятся 1) перенос вдоль оси Ох; 2) перенос вдоль оси Оу; 3) сжатие (растяжение) вдоль оси Ох; 4) сжатие (растяжение) вдоль оси Оу. И как частный случай сжатия – симметрия относительно оси Оу и оси Ох.
Как построить график с помощью линейных преобразований Пусть дан график функции y = f(x). Рассмотрим, как построить график функции y = Аf(аx + b) + B, где А, В, а, b − числа, причем А ≠ 0, а ≠ 0. Обычно строят график этой функции постепенно. 1) Сначала перенос вдоль Ох, 2) затем сжатие (растяжение) к оси Оу, 3) сжатие (растяжение) к оси Ох, 4) перенос вдоль Оу.
Преобразуем 1) 2) 3) 4) Перенос вдоль оси Ох на число − b/a. Сжатие в а раз вдоль оси Ох (к оси Оу). Сжатие в А раз вдоль оси Оу. (к оси Ох). Перенос вдоль оси Оу на число В.
Прежде всего начать следует с О. О. функции, затем функцию преобразовать и выписать 4 (или сколько получится) вспомогательные функции: у1, у2, у3, у4. Затем начертить оси, подписать их, отметить масштаб. Последовательно построить все четыре графика разноцветными карандашами и подписать графики. Это на «пятерку» .
Пример функции у = 1/x В качестве повторения сначала рассмотрим свойства функции у = 1/x. Область определения (− ∞; 0)U(0; +∞). Множество значений Def(y) = (− ∞; 0)U(0; +∞). Нечетная. Док-во. Область определения симметрична относительно 0 и имеет место равенство
Непериодическая (без доказательства) Убывающая Док-во. Пусть два числа х1 и х2 таковы, что х1 < x 2 и оба числа положительны. Надо доказать, что f(x 1) > f(x 2). Рассмотрим разность
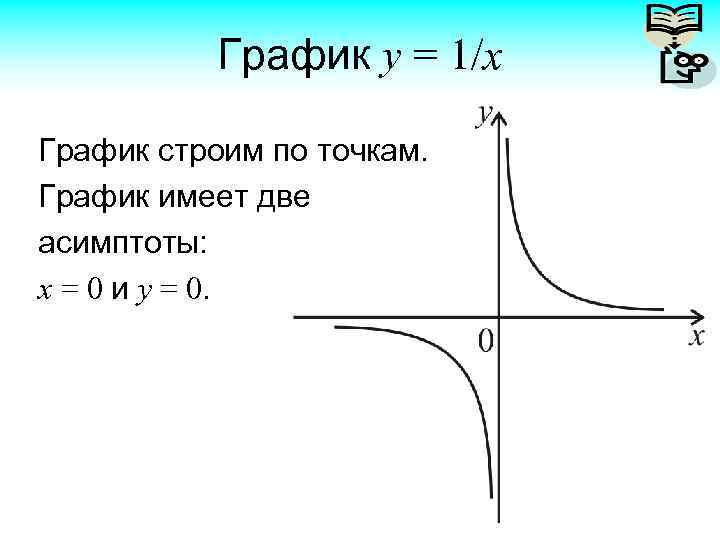
График y = 1/x График строим по точкам. График имеет две асимптоты: х = 0 и у = 0.
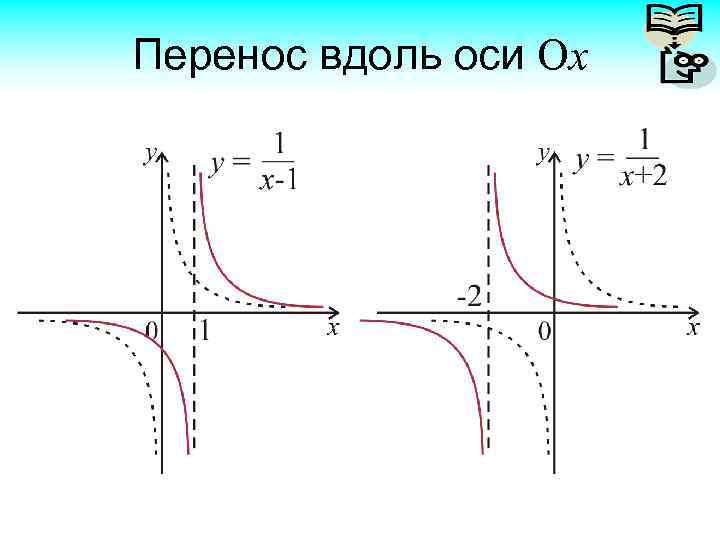
Перенос вдоль оси Ох
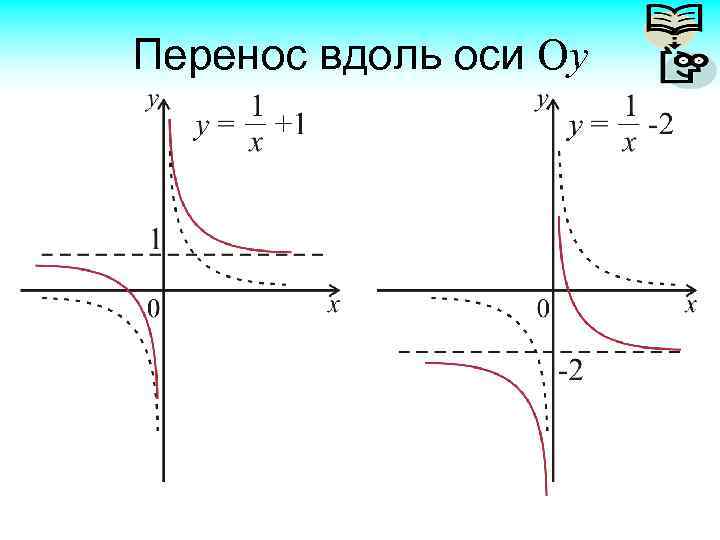
Перенос вдоль оси Оу
Перенос вдоль осей: выводы Пусть дана функция y = f(x). Надо построить график функции y = f(x + c). Это построение реализуется переносом вдоль оси Ох. Если надо построить график функции y = f(x) + В, то это перенос вдоль оси Оу.
Сжатие (растяжение) вдоль оси Ох к оси Оу Пусть дана функция y = f(x). Надо построить график функции y = f(аx), где а ≠ 0. 1) Если а > 1, то сжатие вдоль оси Ох к оси Оу. 2) Если 0 < a < 1, то растяжение вдоль оси Ох в 1/a раз. 3) а = − 1 − это симметрия относительно оси Оу.
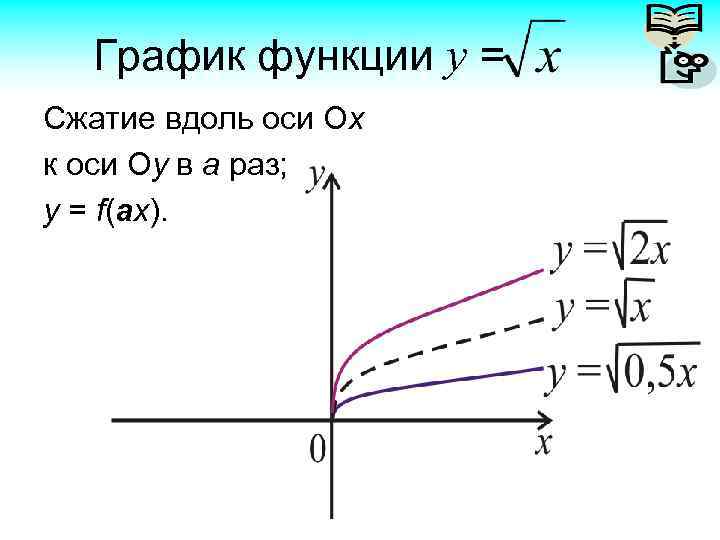
График функции у = Сжатие вдоль оси Ох к оси Оу в а раз; y = f(аx).
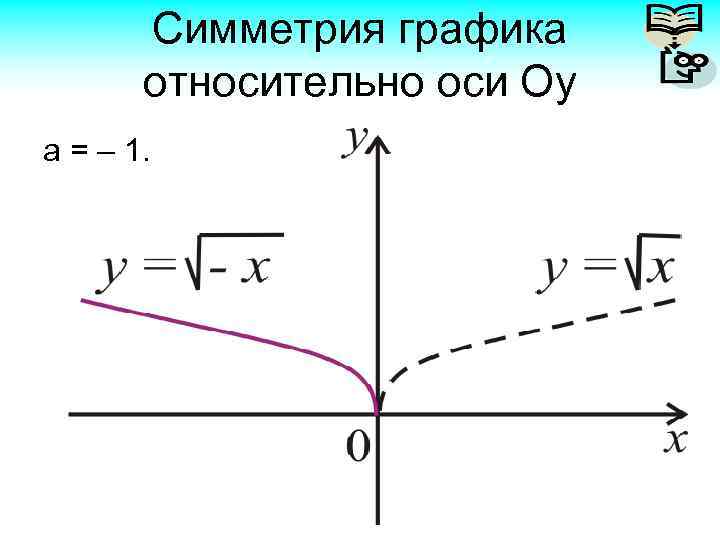
Симметрия графика относительно оси Оу а = – 1.
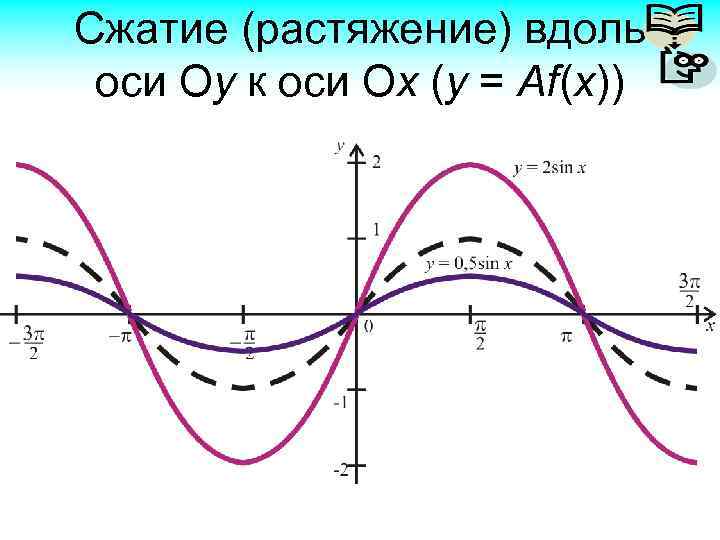
Сжатие (растяжение) вдоль оси Оу к оси Ох (у = Аf(x))
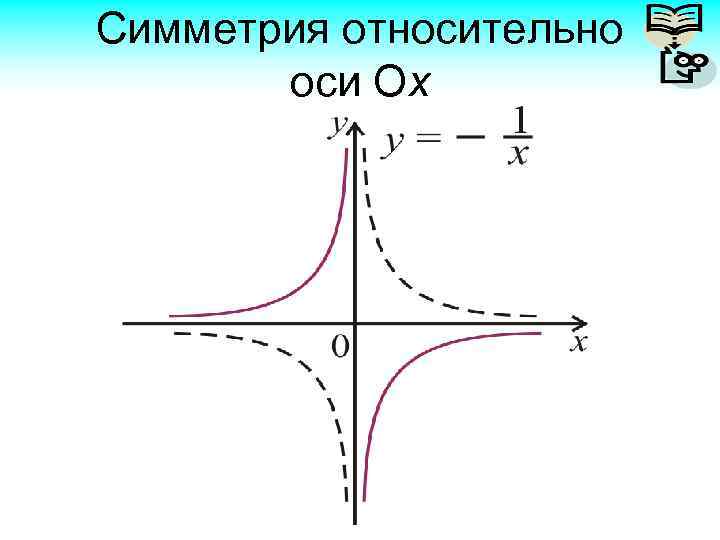
Симметрия относительно оси Ох
Задача. Постройте график функции у = |2 x + 3| 1) Сначала преобразуем у = | 2(x + 3/2)| Или у = 2 | x + 1, 5|. Здесь два преобразования: Перенос вдоль оси Ох на − 1, 5 и сжатие в 2 раза. Построим у1 = | x + 1, 5| и у2 = 2 у1.
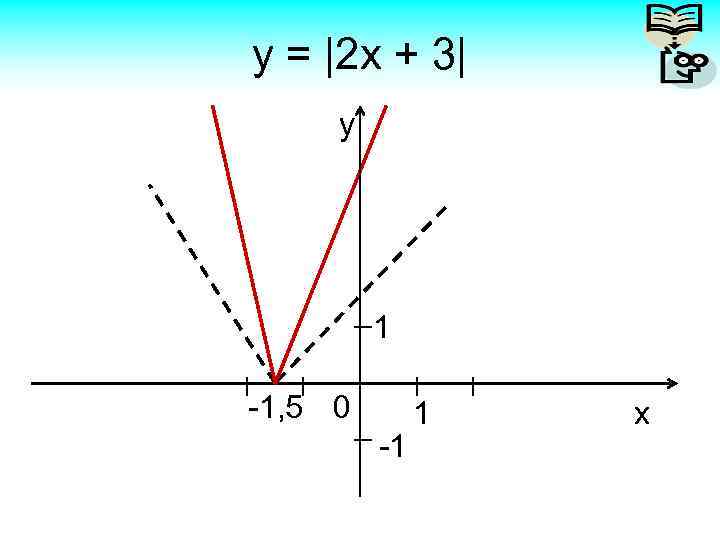
у = |2 x + 3| у 1 -1, 5 0 -1 1 х
Задача. Постройте график функции y = sin(2 x +π/2) Преобразуем y = sin(2(x + π/4)) y 1 = sin(x + π/4) – перенос влево; y 2 = sin(2(x + π/4)) – сжатие. Или второй способ y 1 = sin 2 x y 2 = sin(2 x + π/2) Фактически надо построить график у = cos 2 x.
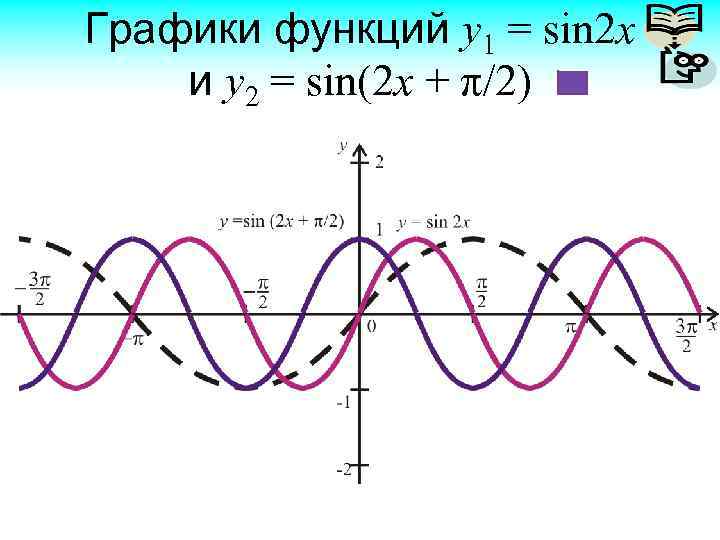
Графики функций y 1 = sin 2 x и y 2 = sin(2 x + π/2)
Задача. Постройте график функции y = Область определения 4 х + 8 ≥ 0, т. е. х ≥ − 2. Преобразуем у = , т. е. у=. Здесь два преобразования: перенос вдоль оси Ох на число − 2 и сжатие в два раза вдоль оси Оу к оси Ох.
Домашнее задание 1. Разобраться с преобразованиями 2. Научиться строить графики с использованием линейных преобразований 3. Получить зачетное задание № 2 на индивидуальной карточке и сделать аккуратно на листочке в клеточку графики функций посредством линейных преобразований. Сдать в понедельник. Подписать!
Скачать презентацию Линейные преобразования графика функции 1 курс 1 семестр
Линейные преобразования графика функции.pptx