Линейные операции в координатной форме.

































































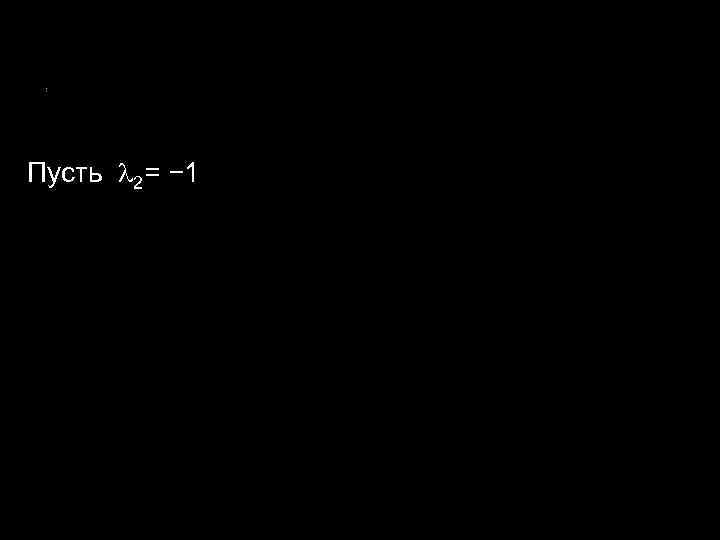























![Примеры. 2)Рассмотрим - множество функций бесконечно дифференцируемых на [0, 1], Примеры. 2)Рассмотрим - множество функций бесконечно дифференцируемых на [0, 1],](https://present5.com/presentation/3/173142797_132636254.pdf-img/173142797_132636254.pdf-96.jpg)




ч.1.лин. алг.(н).ppt
- Количество слайдов: 99
 Линейные операции в координатной форме. Базисом B линейного пространства V называется упорядоченная линейно независимая система векторов из этого пространства, таких, что любой вектор может быть единственным образом представлен в виде линейной комбинации базисных векторов: Данное выражение называется разложением вектора по базису
Линейные операции в координатной форме. Базисом B линейного пространства V называется упорядоченная линейно независимая система векторов из этого пространства, таких, что любой вектор может быть единственным образом представлен в виде линейной комбинации базисных векторов: Данное выражение называется разложением вектора по базису
 В линейном пространстве V может быть задано несколько базисов, но все базисы пространства V состоят из одинакового числа векторов. Если базис пространства V состоит из n векторов, то говорят, что пространство n-мерно. dim. V=n.
В линейном пространстве V может быть задано несколько базисов, но все базисы пространства V состоят из одинакового числа векторов. Если базис пространства V состоит из n векторов, то говорят, что пространство n-мерно. dim. V=n.
 Пусть в линейном пространстве Vn задан базис Тогда для любых элементов и Утверждение:
Пусть в линейном пространстве Vn задан базис Тогда для любых элементов и Утверждение:
 Доказательство: ◄ ►
Доказательство: ◄ ►
 Пусть в линейном пространстве V заданы два базиса: и Векторы Их можно разложить по базису
Пусть в линейном пространстве V заданы два базиса: и Векторы Их можно разложить по базису
 Составим матрицу , j-ый столбец которой есть координаты вектора в базисе B: Матрица называется матрицей перехода от базиса B к базису B'. Матрица перехода невырожденная, так как базисные векторы линейно независимы.
Составим матрицу , j-ый столбец которой есть координаты вектора в базисе B: Матрица называется матрицей перехода от базиса B к базису B'. Матрица перехода невырожденная, так как базисные векторы линейно независимы.
 Пусть Тот же элемент в новом базисе B': Тогда
Пусть Тот же элемент в новом базисе B': Тогда
 В силу единственности разложения вектора по базису имеем:
В силу единственности разложения вектора по базису имеем:
 Координаты вектора в базисе B находим по формуле: где -координаты вектора в базисе B' ; -координаты вектора в базисе B.
Координаты вектора в базисе B находим по формуле: где -координаты вектора в базисе B' ; -координаты вектора в базисе B.
 Пример. Даны два базиса: Найти матрицу перехода от базиса В к базису В'. Решение. ►Пусть - стандартный канонический базис. Тогда
Пример. Даны два базиса: Найти матрицу перехода от базиса В к базису В'. Решение. ►Пусть - стандартный канонический базис. Тогда
 Так как , то Таким образом:
Так как , то Таким образом:
 ►
►
 Линейные отображения линейных пространств. Пусть V и W – линейные пространства размерности m и n. Определение. Отображение f: V→W, сопоставляющее каждому элементу линейного пространства V некоторый элемент линейного пространства W, называется линейным, если для
Линейные отображения линейных пространств. Пусть V и W – линейные пространства размерности m и n. Определение. Отображение f: V→W, сопоставляющее каждому элементу линейного пространства V некоторый элемент линейного пространства W, называется линейным, если для
 Примеры: 1. где а = const; 2. где вектор фиксированный единичный вектор пространства 3. Пусть V=W=Pn – пространство многочленов, степень которых не выше n. Каждому многочлену из Pn ставится в соответствие его производная: Данное отображение является линейным, так как производная суммы равна сумме производных, а постоянный множитель можно вынести из-под знака производной.
Примеры: 1. где а = const; 2. где вектор фиксированный единичный вектор пространства 3. Пусть V=W=Pn – пространство многочленов, степень которых не выше n. Каждому многочлену из Pn ставится в соответствие его производная: Данное отображение является линейным, так как производная суммы равна сумме производных, а постоянный множитель можно вынести из-под знака производной.
 4. Умножение матрицы А размера m×n на произвольный столбец X высоты n справа является линейным отображением пространства столбцов высоты n в пространство столбцов высоты m:
4. Умножение матрицы А размера m×n на произвольный столбец X высоты n справа является линейным отображением пространства столбцов высоты n в пространство столбцов высоты m:
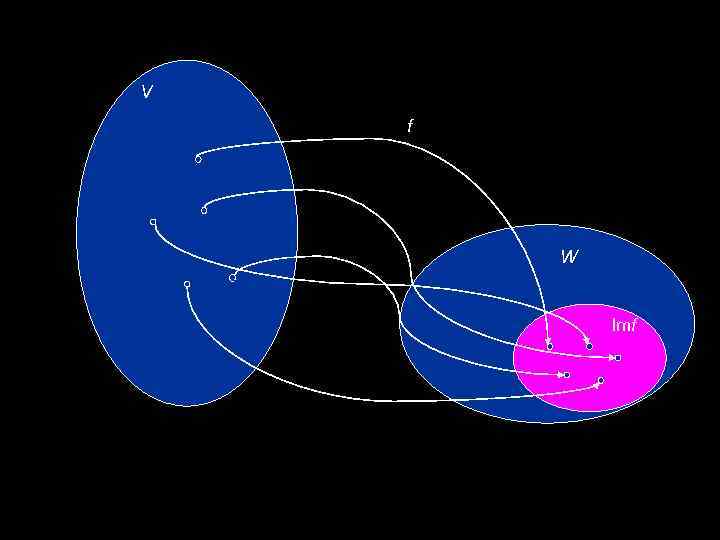
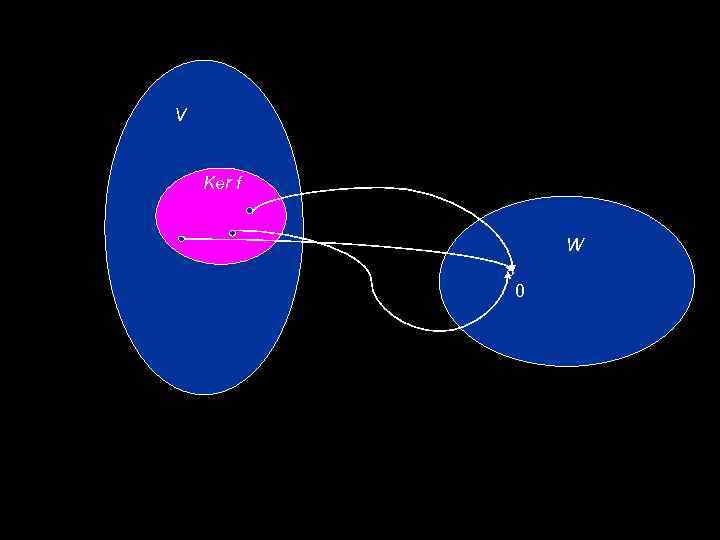
 Ядро и образ линейного отображения. Определение. Образом линейного отображения f: V→W называется множество всех элементов из линейного пространства W, обладающих следующим свойством: , если в пространстве V существует элемент , такой что Определение. Ядром линейного отображения f: V→W называется множество всех элементов из линейного пространства V, каждый из которых линейное отображение f переводит в нулевой вектор линейного пространства W.
Ядро и образ линейного отображения. Определение. Образом линейного отображения f: V→W называется множество всех элементов из линейного пространства W, обладающих следующим свойством: , если в пространстве V существует элемент , такой что Определение. Ядром линейного отображения f: V→W называется множество всех элементов из линейного пространства V, каждый из которых линейное отображение f переводит в нулевой вектор линейного пространства W.
 V f W Imf
V f W Imf
 V Ker f W 0
V Ker f W 0
 Свойства ядра и образа 1. Образ линейного отображения f: V→W является линейным подпространством пространства W. 2. Ядро линейного отображения f: V→W является линейным подпространством пространства V. 3. Размерность образа линейного отображения называется рангом этого отображения dim Im f = rf , а размерность ядра называется дефектом dim Ker f = n f.
Свойства ядра и образа 1. Образ линейного отображения f: V→W является линейным подпространством пространства W. 2. Ядро линейного отображения f: V→W является линейным подпространством пространства V. 3. Размерность образа линейного отображения называется рангом этого отображения dim Im f = rf , а размерность ядра называется дефектом dim Ker f = n f.
 Пример. Образом отображения дифференцирования в пространстве Pn является совокупность, многочленов, степени не выше n-1 , а ядром этого отображения является множество многочленов нулевой степени.
Пример. Образом отображения дифференцирования в пространстве Pn является совокупность, многочленов, степени не выше n-1 , а ядром этого отображения является множество многочленов нулевой степени.
 Линейные операторы. Линейным оператором в линейном пространстве V называется любое отображение : V V пространства V в себя, обладающее следующими свойствами: Примеры линейных операторов. 1. Оператор дифференцирования. Пусть V=Pn – пространство многочленов, степень которых не выше n. Каждому многочлену из Pn ставится в соответствие его производная:
Линейные операторы. Линейным оператором в линейном пространстве V называется любое отображение : V V пространства V в себя, обладающее следующими свойствами: Примеры линейных операторов. 1. Оператор дифференцирования. Пусть V=Pn – пространство многочленов, степень которых не выше n. Каждому многочлену из Pn ставится в соответствие его производная:
 2. Оператор поворота на угол φ на плоскости против часовой стрелки. 3. Оператор проектирования на заданную плоскость в пространстве R³.
2. Оператор поворота на угол φ на плоскости против часовой стрелки. 3. Оператор проектирования на заданную плоскость в пространстве R³.
 Ядро и образ линейного оператора. Определение. Образом линейного оператора : V→V называется множество Размерность образа линейного оператора называется рангом. Определение. Ядром линейного оператора : V→V называется множество Размерность ядра линейного оператора называется дефектом.
Ядро и образ линейного оператора. Определение. Образом линейного оператора : V→V называется множество Размерность образа линейного оператора называется рангом. Определение. Ядром линейного оператора : V→V называется множество Размерность ядра линейного оператора называется дефектом.
 Операции над линейными операторами и их матрицами. В множестве всех линейных операторов, дейст- вующих в линейном пространстве V, определены операции суммы и умножения операторов на число. Определение. Суммой линейных операторов и , действующих в линейном пространстве V, называется линейный оператор : V→V, определяемый равенством Определение. Произведением линейного оператора на число λ называется линейный оператор λ : V→V, определяемый равенством
Операции над линейными операторами и их матрицами. В множестве всех линейных операторов, дейст- вующих в линейном пространстве V, определены операции суммы и умножения операторов на число. Определение. Суммой линейных операторов и , действующих в линейном пространстве V, называется линейный оператор : V→V, определяемый равенством Определение. Произведением линейного оператора на число λ называется линейный оператор λ : V→V, определяемый равенством
 Определение. Нулевым оператором называется линейный оператор Ô: V→V, отображающий все элементы линейного пространства V в нулевой вектор: Определение. Линейный оператор Ê: V→V, называется тождественным, если Определение. Линейный оператор (− ): V→V называется противоположным к линейному оператору : V→V, если
Определение. Нулевым оператором называется линейный оператор Ô: V→V, отображающий все элементы линейного пространства V в нулевой вектор: Определение. Линейный оператор Ê: V→V, называется тождественным, если Определение. Линейный оператор (− ): V→V называется противоположным к линейному оператору : V→V, если
 Замечание. Множество всех линейных операторов, действующих в линейном пространстве V , с указанными выше операциями суммы и умножения на скаляр, является линейным пространством. Определение. Пусть и - линейные операторы, действующие в линейном пространстве V. Произведением линейного оператора на линейный оператор называется оператор , действующий в линейном пространстве V по правилу: Корректность определения:
Замечание. Множество всех линейных операторов, действующих в линейном пространстве V , с указанными выше операциями суммы и умножения на скаляр, является линейным пространством. Определение. Пусть и - линейные операторы, действующие в линейном пространстве V. Произведением линейного оператора на линейный оператор называется оператор , действующий в линейном пространстве V по правилу: Корректность определения:
 Свойства: Определение. Линейный оператор Ĉ: V→V называется обратным для линейного оператора : V→V , если
Свойства: Определение. Линейный оператор Ĉ: V→V называется обратным для линейного оператора : V→V , если
 Утверждение. Для того, чтобы линейный оператор имел обратный необходимо и достаточно, чтобы образ данного оператора совпадал со всем линейным пространством V. Следствие. Линейный оператор обратим тогда и только тогда, когда его ядро тривиально,
Утверждение. Для того, чтобы линейный оператор имел обратный необходимо и достаточно, чтобы образ данного оператора совпадал со всем линейным пространством V. Следствие. Линейный оператор обратим тогда и только тогда, когда его ядро тривиально,
 Матрица линейного оператора. Пусть тогда
Матрица линейного оператора. Пусть тогда
 В силу единственности разложения вектора по базису получим: Тогда матрица называется матрицей оператора в базисе B. Столбцами этой матрицы являются координаты образов базисных векторов при действии линейного оператора.
В силу единственности разложения вектора по базису получим: Тогда матрица называется матрицей оператора в базисе B. Столбцами этой матрицы являются координаты образов базисных векторов при действии линейного оператора.
 Замечания. 1. Если оператор нулевой, то все элементы матрицы этого оператора равны 0 в любом базисе. 2. Если оператор единичный (тождественный), то матрица этого оператора также единичная. 3. При сложении линейных операторов их матрицы (заданные в одном и том же базисе) складываются, а при умножении линейного оператора на число его матрица умножается на это число. 4. Матрица произведения операторов и Ĉ равна произведению матриц данных операторов: С·А.
Замечания. 1. Если оператор нулевой, то все элементы матрицы этого оператора равны 0 в любом базисе. 2. Если оператор единичный (тождественный), то матрица этого оператора также единичная. 3. При сложении линейных операторов их матрицы (заданные в одном и том же базисе) складываются, а при умножении линейного оператора на число его матрица умножается на это число. 4. Матрица произведения операторов и Ĉ равна произведению матриц данных операторов: С·А.
 Таким образом, мы установили, что каждому л. о. : V→V при заданном базисе линейного пространства V размерности n соответствует матрица А размера n x n. И обратно, для любой матрицы А размера n x n существует и при том единственный л. о. , матрицей которого в заданном базисе является матрица А. То есть между множеством матриц размера n x n и множеством линейных операторов : V→V существует взаимно однозначное соответствие. Действия с линейными операторами сводятся к соответствующим действиям с их матрицами.
Таким образом, мы установили, что каждому л. о. : V→V при заданном базисе линейного пространства V размерности n соответствует матрица А размера n x n. И обратно, для любой матрицы А размера n x n существует и при том единственный л. о. , матрицей которого в заданном базисе является матрица А. То есть между множеством матриц размера n x n и множеством линейных операторов : V→V существует взаимно однозначное соответствие. Действия с линейными операторами сводятся к соответствующим действиям с их матрицами.
 Примеры:
Примеры:
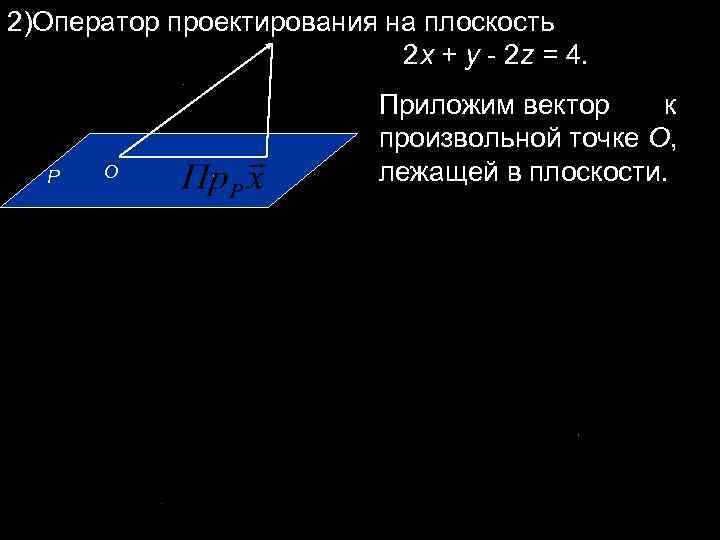
 2)Оператор проектирования на плоскость 2 x + y - 2 z = 4. Приложим вектор к произвольной точке О, P O лежащей в плоскости.
2)Оператор проектирования на плоскость 2 x + y - 2 z = 4. Приложим вектор к произвольной точке О, P O лежащей в плоскости.
 3)Оператор проектирования на плоскость XOY.
3)Оператор проектирования на плоскость XOY.
 Формула преобразования матрицы линейного оператора при преобразовании базиса: Пусть в линейном пространстве V заданы два базиса: А– матрица линейного оператора в базисе B; А – матрица этого же л. оператора в базисе B , – матрица перехода от базиса B к B.
Формула преобразования матрицы линейного оператора при преобразовании базиса: Пусть в линейном пространстве V заданы два базиса: А– матрица линейного оператора в базисе B; А – матрица этого же л. оператора в базисе B , – матрица перехода от базиса B к B.
 Получили формулу преобразования матрицы л. о. при преобразовании базиса: Собственные векторы и собственные числа линейного оператора. Их свойства. Определение. Ненулевой вектор называется собственным вектором линейного оператора : V→V , если Число λ - собственное значение л. о. , отвечающее собственному вектору
Получили формулу преобразования матрицы л. о. при преобразовании базиса: Собственные векторы и собственные числа линейного оператора. Их свойства. Определение. Ненулевой вектор называется собственным вектором линейного оператора : V→V , если Число λ - собственное значение л. о. , отвечающее собственному вектору
 Утверждение. Множество собственных векторов л. о. , отвечающих одному и тому же собственному значению λ, дополненное нулевым вектором, является линейным подпространством линейного пространства V. Доказательство. ◄Пусть и - собственные векторы л. о. , отвечающие собственному значению λ. Тогда - собственный вектор линейного оператора . ►
Утверждение. Множество собственных векторов л. о. , отвечающих одному и тому же собственному значению λ, дополненное нулевым вектором, является линейным подпространством линейного пространства V. Доказательство. ◄Пусть и - собственные векторы л. о. , отвечающие собственному значению λ. Тогда - собственный вектор линейного оператора . ►
 Примеры. 1. Найти собственные числа и собственные векторы оператора проектирования на плоскость XOY в . Решение. Пусть PXOY - оператор проектирования на плоскость XOY, а - собственный вектор этого оператора. Тогда Это означает, что ортогональная проекция вектора на плоскость XOY коллинеарна вектору Возможны два случая: 1. и вектор коллинеарен плоскости XOY. Для всех таких векторов то есть они являются собственными векторами л. о. , отвечающими собственному значению λ=1.
Примеры. 1. Найти собственные числа и собственные векторы оператора проектирования на плоскость XOY в . Решение. Пусть PXOY - оператор проектирования на плоскость XOY, а - собственный вектор этого оператора. Тогда Это означает, что ортогональная проекция вектора на плоскость XOY коллинеарна вектору Возможны два случая: 1. и вектор коллинеарен плоскости XOY. Для всех таких векторов то есть они являются собственными векторами л. о. , отвечающими собственному значению λ=1.
 2. и вектор ортогонален плоскости XOY. Для всех таких векторов то есть они являются собственными векторами л. о. , отвечающими собственному значению λ=0. В итоге получили, что оператор проектирования на плоскость XOY имеет два собственных значения: λ 1 =1 и λ 2=0, соответствующие им собственные векторы:
2. и вектор ортогонален плоскости XOY. Для всех таких векторов то есть они являются собственными векторами л. о. , отвечающими собственному значению λ=0. В итоге получили, что оператор проектирования на плоскость XOY имеет два собственных значения: λ 1 =1 и λ 2=0, соответствующие им собственные векторы:
 2. Найти собственные числа и собственные векторы оператора поворота на угол φ вокруг начала координат против часовой стрелки в пространстве Решение. Пусть Uφ- оператор поворота на угол φ (0 ≤ φ < 2 ) , а - собственный вектор этого оператора. Y При φ≠ 0 и φ≠ данный оператор не имеет собственных φ векторов, так как ни один вектор не перейдет ни в коллинеарный ему вектор, ни в нулевой вектор. O X При φ=0 а при
2. Найти собственные числа и собственные векторы оператора поворота на угол φ вокруг начала координат против часовой стрелки в пространстве Решение. Пусть Uφ- оператор поворота на угол φ (0 ≤ φ < 2 ) , а - собственный вектор этого оператора. Y При φ≠ 0 и φ≠ данный оператор не имеет собственных φ векторов, так как ни один вектор не перейдет ни в коллинеарный ему вектор, ни в нулевой вектор. O X При φ=0 а при
 Характеристический многочлен, его независимость от выбора базиса. Пусть А – матрица линейного оператора в некотором базисе линейного пространства V. Функция является многочленом от λ и называется характеристическим многочленом л. о. . Коэффициент равный сумме диагональных элементов матрицы А называется следом линейного оператора и обозначается tr. A.
Характеристический многочлен, его независимость от выбора базиса. Пусть А – матрица линейного оператора в некотором базисе линейного пространства V. Функция является многочленом от λ и называется характеристическим многочленом л. о. . Коэффициент равный сумме диагональных элементов матрицы А называется следом линейного оператора и обозначается tr. A.
 Утверждение. Определитель матрицы линейного оператора не зависит от выбора базиса. Доказательство. ◄ Пусть в линейном пространстве V заданы два базиса: А– матрица линейного оператора в базисе B; А – матрица этого же линейного оператора в базисе B , матрица перехода от базиса B к B. Тогда Вычислим определитель матрицы А': так как ►
Утверждение. Определитель матрицы линейного оператора не зависит от выбора базиса. Доказательство. ◄ Пусть в линейном пространстве V заданы два базиса: А– матрица линейного оператора в базисе B; А – матрица этого же линейного оператора в базисе B , матрица перехода от базиса B к B. Тогда Вычислим определитель матрицы А': так как ►
 Утверждение. Характеристические многочлены подобных матриц совпадают. Доказательство. ◄ ►
Утверждение. Характеристические многочлены подобных матриц совпадают. Доказательство. ◄ ►
 Отыскание собственных чисел и собственных векторов линейного оператора. Теорема 1. Пусть А – матрица линейного оператора в некотором базисе линейного пространства V. Тогда – собственное значение л. о. тогда и только тогда, когда – корень уравнения det(A – Е) = 0. Это уравнение называется характеристическим и записывается в виде:
Отыскание собственных чисел и собственных векторов линейного оператора. Теорема 1. Пусть А – матрица линейного оператора в некотором базисе линейного пространства V. Тогда – собственное значение л. о. тогда и только тогда, когда – корень уравнения det(A – Е) = 0. Это уравнение называется характеристическим и записывается в виде:
 Доказательство: ◄ 1. Пусть λ – собственное значение л. о. Однородная система линейных уравнений имеет ненулевое решение, если rang(A− E) < n det(A− E) = 0.
Доказательство: ◄ 1. Пусть λ – собственное значение л. о. Однородная система линейных уравнений имеет ненулевое решение, если rang(A− E) < n det(A− E) = 0.
 2. Пусть λ – корень уравнения det(A − E)=0 Система имеет ненулевое решение λ – собственное значение л. о. . ► Замечание. Собственные векторы, отвечающие собственному значению , можно найти, построив фундаментальную систему решений однородной системы линейных уравнений или записанную в виде:
2. Пусть λ – корень уравнения det(A − E)=0 Система имеет ненулевое решение λ – собственное значение л. о. . ► Замечание. Собственные векторы, отвечающие собственному значению , можно найти, построив фундаментальную систему решений однородной системы линейных уравнений или записанную в виде:
 Примеры. 1. Найти собственные числа и собственные векторы оператора проектирования на плоскость XOY в . Решение. Запишем матрицу оператора проектирования на плоскость XOY: Найдем det(PXOY− E):
Примеры. 1. Найти собственные числа и собственные векторы оператора проектирования на плоскость XOY в . Решение. Запишем матрицу оператора проектирования на плоскость XOY: Найдем det(PXOY− E):
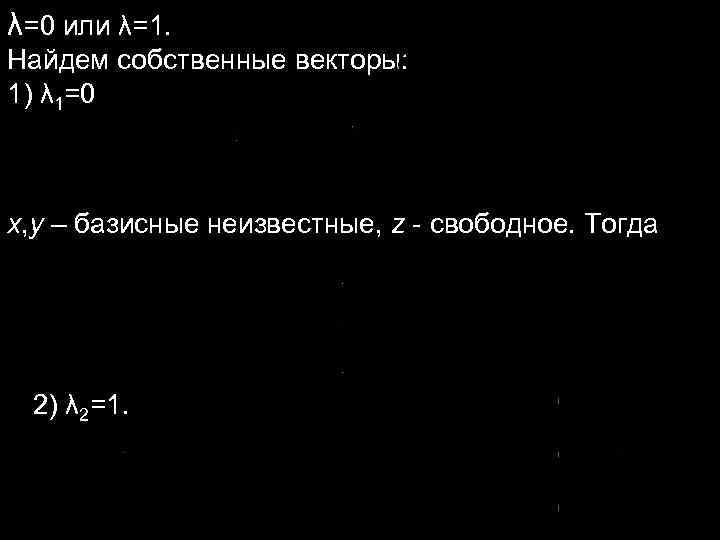
 λ=0 или λ=1. Найдем собственные векторы: 1) λ 1=0 x, y – базисные неизвестные, z - свободное. Тогда 2) λ 2=1.
λ=0 или λ=1. Найдем собственные векторы: 1) λ 1=0 x, y – базисные неизвестные, z - свободное. Тогда 2) λ 2=1.
 z– базисное неизвестное, x, y - свободные неизвестные. Тогда 2. Найти собственные числа и собственные векторы оператора поворота на угол φ вокруг начала координат против часовой стрелки в пространстве Решение. Запишем матрицу оператора на угол φ вокруг начала координат против часовой стрелки в пространстве
z– базисное неизвестное, x, y - свободные неизвестные. Тогда 2. Найти собственные числа и собственные векторы оператора поворота на угол φ вокруг начала координат против часовой стрелки в пространстве Решение. Запишем матрицу оператора на угол φ вокруг начала координат против часовой стрелки в пространстве
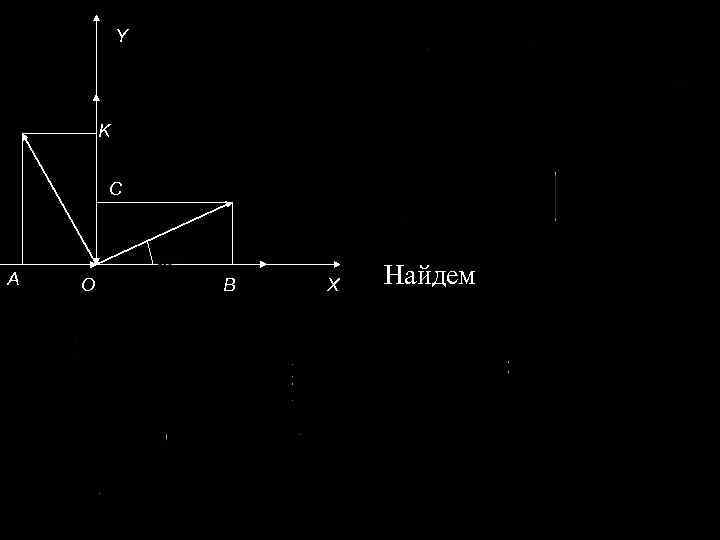
 Y K C A O B X Найдем
Y K C A O B X Найдем
 Теорема 2. Собственные векторы, отвечающие различным собственным значениям л. о. , линейно независимы. Доказательство: ◄ Пусть − собственные значения л. о. , причем − собственные векторы л. о. , отвечающие собственным значениям т. е. Докажем методом математической индукции. Очевидно, что линейно независим, так как Предположим, что векторы линейно независимы и докажем, что векторы линейно независимы.
Теорема 2. Собственные векторы, отвечающие различным собственным значениям л. о. , линейно независимы. Доказательство: ◄ Пусть − собственные значения л. о. , причем − собственные векторы л. о. , отвечающие собственным значениям т. е. Докажем методом математической индукции. Очевидно, что линейно независим, так как Предположим, что векторы линейно независимы и докажем, что векторы линейно независимы.
 Составим их линейную комбинацию: Подействуем на данное выражение л. о. : - линейный оператор, следовательно, Так как то
Составим их линейную комбинацию: Подействуем на данное выражение л. о. : - линейный оператор, следовательно, Так как то
 Из выражения (2) вычтем выражение (1), умноженное на k: Так как i k (при i k) по условию, а векторы линейно независимы по предположению индукции, то Получили, что все векторы линейно независимы.
Из выражения (2) вычтем выражение (1), умноженное на k: Так как i k (при i k) по условию, а векторы линейно независимы по предположению индукции, то Получили, что все векторы линейно независимы.
 Теорема 3. Матрица линейного оператора в базисе диагональная, тогда и только тогда, когда векторы - собственные векторы л. о. Доказательство: ◄ 1. Пусть - собственные векторы л. о. , т. е. Вектор
Теорема 3. Матрица линейного оператора в базисе диагональная, тогда и только тогда, когда векторы - собственные векторы л. о. Доказательство: ◄ 1. Пусть - собственные векторы л. о. , т. е. Вектор
 Матрица л. о. – диагональная. 2. Пусть матрица л. о. – диагональная, т. е. - собственный вектор л. о. . ►
Матрица л. о. – диагональная. 2. Пусть матрица л. о. – диагональная, т. е. - собственный вектор л. о. . ►
 Следствие 1. Если л. о. : V→V (dim V = n) имеет n различных собственных значений, то в базисе из собственных векторов матрица этого линейного оператора имеет диагональный вид. Доказательство. ◄Для каждого собственного значения можно найти собственный вектор. По теореме 2 собственные векторы, отвечающие различным собственным значениям, линейно независимы, а так количество собственных векторов равно размерности линейного пространства, то система выбранных таким образом собственных векторов образует базис этого пространства. По теореме 3 матрица линейного оператора в этом базисе имеет диагональный вид. ►
Следствие 1. Если л. о. : V→V (dim V = n) имеет n различных собственных значений, то в базисе из собственных векторов матрица этого линейного оператора имеет диагональный вид. Доказательство. ◄Для каждого собственного значения можно найти собственный вектор. По теореме 2 собственные векторы, отвечающие различным собственным значениям, линейно независимы, а так количество собственных векторов равно размерности линейного пространства, то система выбранных таким образом собственных векторов образует базис этого пространства. По теореме 3 матрица линейного оператора в этом базисе имеет диагональный вид. ►
 Следствие 2. Если характеристическое уравнение квадратной матрицы размера n× n имеет ровно n попарно различных действительных корней, то эта матрица подобна некоторой диагональной матрице. Замечания. 1. Замена матрицы А диагональной матрицей А', подобной матрице А, называется приведением матрицы А к диагональному виду. 2. Если характеристическое уравнение линейного оператора имеет кратные действительные корни, то такой линейный оператор может иметь диагональную матрицу в некотором базисе, но так бывает не всегда.
Следствие 2. Если характеристическое уравнение квадратной матрицы размера n× n имеет ровно n попарно различных действительных корней, то эта матрица подобна некоторой диагональной матрице. Замечания. 1. Замена матрицы А диагональной матрицей А', подобной матрице А, называется приведением матрицы А к диагональному виду. 2. Если характеристическое уравнение линейного оператора имеет кратные действительные корни, то такой линейный оператор может иметь диагональную матрицу в некотором базисе, но так бывает не всегда.
 Приведение матрицы линейного оператора к диагональному виду. Рассмотрим два линейных оператора, матрицы которых в некотором базисе имеют вид: Характеристические уравнения этих операторов совпадают: Оба эти оператора имеют собственное значение λ=2 кратности 2. Матрица первого линейного оператора уже имеет диагональный вид, то есть исходный базис состоит из собственных векторов этого оператора.
Приведение матрицы линейного оператора к диагональному виду. Рассмотрим два линейных оператора, матрицы которых в некотором базисе имеют вид: Характеристические уравнения этих операторов совпадают: Оба эти оператора имеют собственное значение λ=2 кратности 2. Матрица первого линейного оператора уже имеет диагональный вид, то есть исходный базис состоит из собственных векторов этого оператора.
 Можно показать, что любой ненулевой вектор для этого оператора является собственным и поэтому для него любой базис является базисом из собственных векторов. У второго л. о. все собственные векторы, отвечают собст. значению λ=2, но размерность собственного подпространства линейного оператора для этого собственного значения одномерно. Следовательно, найти два линейно независимых собственных вектора для этого линейного оператора невозможно, и базиса из собственных векторов не существует.
Можно показать, что любой ненулевой вектор для этого оператора является собственным и поэтому для него любой базис является базисом из собственных векторов. У второго л. о. все собственные векторы, отвечают собст. значению λ=2, но размерность собственного подпространства линейного оператора для этого собственного значения одномерно. Следовательно, найти два линейно независимых собственных вектора для этого линейного оператора невозможно, и базиса из собственных векторов не существует.
 Определение. Пусть i – корень характер. уравнения det(A− E)=0 кратности ki, то есть Тогда ki – алгебраическая кратность собственного значения i , то есть кратность i как корня характеристического уравнения. Рассмотрим подпространство - подпространство линейного пространства V , состоящее из всех собственных векторов, соответствующих собственному значению i , дополненное нулевым вектором.
Определение. Пусть i – корень характер. уравнения det(A− E)=0 кратности ki, то есть Тогда ki – алгебраическая кратность собственного значения i , то есть кратность i как корня характеристического уравнения. Рассмотрим подпространство - подпространство линейного пространства V , состоящее из всех собственных векторов, соответствующих собственному значению i , дополненное нулевым вектором.
 Если собственное подпространство линейного пространства V, соответствующее собственному значению i . Определение. геометрическая кратность собственного значения i.
Если собственное подпространство линейного пространства V, соответствующее собственному значению i . Определение. геометрическая кратность собственного значения i.
 Если рассмотреть систему линейных уравнений то однородная С. Л. У. , с определителем равным нулю, имеет нетривиальное решение. Линейное пространство всех решений этой системы совпадает с собственным подпространством
Если рассмотреть систему линейных уравнений то однородная С. Л. У. , с определителем равным нулю, имеет нетривиальное решение. Линейное пространство всех решений этой системы совпадает с собственным подпространством
 Теорема 1. Геометрическая кратность собственного значения не превосходит его алгебраической кратности. Теорема 2. Пусть - линейный оператор, действующий в линейном пространстве V. Для существования базиса из собственных векторов необходимо и достаточно выполнения следующих условий: 1) все корни характеристического уравнения вещественны; 2)геометрическая кратность каждого собственного значения совпадает с его алгебраической кратностью.
Теорема 1. Геометрическая кратность собственного значения не превосходит его алгебраической кратности. Теорема 2. Пусть - линейный оператор, действующий в линейном пространстве V. Для существования базиса из собственных векторов необходимо и достаточно выполнения следующих условий: 1) все корни характеристического уравнения вещественны; 2)геометрическая кратность каждого собственного значения совпадает с его алгебраической кратностью.
 Следствие. В базисе из собственных векторов матрица линейного оператора диагональная, причем на главной диагонали стоят соответствующие собственные значения с учетом их кратностей:
Следствие. В базисе из собственных векторов матрица линейного оператора диагональная, причем на главной диагонали стоят соответствующие собственные значения с учетом их кратностей:
 Примеры. Выяснить возможность приведения матрицы линейного оператора к диагональному виду. 1. Решение. 1)Найдем собственные числа л. о. . 1= 1 −корень кратности 2; 1= 2 − кратности 1.
Примеры. Выяснить возможность приведения матрицы линейного оператора к диагональному виду. 1. Решение. 1)Найдем собственные числа л. о. . 1= 1 −корень кратности 2; 1= 2 − кратности 1.
 2) Найдем собственные векторы. Пусть 1= 1, тогда Геометрическая кратность собственного значения 1= 1 меньше его алгебраической кратности, следовательно, базиса из собственных векторов не существует, а значит, данный оператор нельзя привести к диагональному виду.
2) Найдем собственные векторы. Пусть 1= 1, тогда Геометрическая кратность собственного значения 1= 1 меньше его алгебраической кратности, следовательно, базиса из собственных векторов не существует, а значит, данный оператор нельзя привести к диагональному виду.
 2. Решение. 1)Найдем собственные числа л. о. Ĉ.
2. Решение. 1)Найдем собственные числа л. о. Ĉ.
 1= 1 − корень кратности 2; 2= − 1 корень кратности 1. 2) Найдем собственные векторы. Пусть 1= 1, тогда Геометрическая кратность собственного значения 1= 1 равна его алгебраической кратности. Получили собственные векторы:
1= 1 − корень кратности 2; 2= − 1 корень кратности 1. 2) Найдем собственные векторы. Пусть 1= 1, тогда Геометрическая кратность собственного значения 1= 1 равна его алгебраической кратности. Получили собственные векторы:
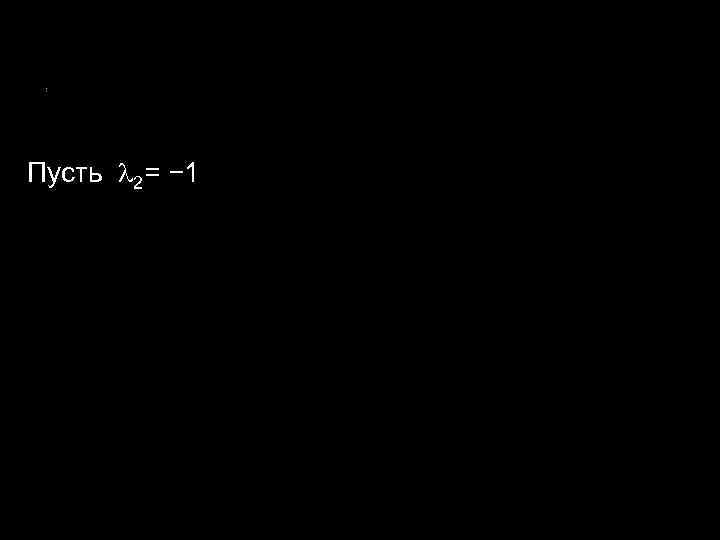 Пусть 2= − 1
Пусть 2= − 1
 Получили базис из собственных векторов: Все собственные значения л. о. вещественны и алгебраические кратности каждого из них совпадают с геометрическими кратностями, значит, данный оператор можно привести к диагональному виду:
Получили базис из собственных векторов: Все собственные значения л. о. вещественны и алгебраические кратности каждого из них совпадают с геометрическими кратностями, значит, данный оператор можно привести к диагональному виду:
 Понятие о евклидовом пространстве, свойства нормы элемента. Определение. Скалярным произведением в вещественном линейном пространстве V называется функция , такая что каждой паре элементов и из этого пространства поставлено в соответствие действительное число так, что для и для
Понятие о евклидовом пространстве, свойства нормы элемента. Определение. Скалярным произведением в вещественном линейном пространстве V называется функция , такая что каждой паре элементов и из этого пространства поставлено в соответствие действительное число так, что для и для
 Следствия. Доказательство свойства 5.
Следствия. Доказательство свойства 5.
 Замечание. Понятие скалярного произведения обобщает понятие скалярного произведения геометрических векторов. Определение. Евклидовым пространством называется вещественное линейное пространство, в котором задана операция скалярного произведения. Обозначения: (V, < >) или E. - евклидово пространство размерности n. Определение. Длиной(нормой) элемента называется число
Замечание. Понятие скалярного произведения обобщает понятие скалярного произведения геометрических векторов. Определение. Евклидовым пространством называется вещественное линейное пространство, в котором задана операция скалярного произведения. Обозначения: (V, < >) или E. - евклидово пространство размерности n. Определение. Длиной(нормой) элемента называется число
 Определение. Элемент, длина которого равна 1, называется нормированным. Примеры евклидовых пространств. 1. Линейное пространство геометрических векторов с обычным скалярным произведением. 2. Пространство строк длины n, где 3. С [0, 1] – пространство функций непрерывных на отрезке [0, 1] со скалярным произведением:
Определение. Элемент, длина которого равна 1, называется нормированным. Примеры евклидовых пространств. 1. Линейное пространство геометрических векторов с обычным скалярным произведением. 2. Пространство строк длины n, где 3. С [0, 1] – пространство функций непрерывных на отрезке [0, 1] со скалярным произведением:
 Определение. Система векторов называется ортогональной, если при Определение. Система векторов называется ортонормированной, если
Определение. Система векторов называется ортогональной, если при Определение. Система векторов называется ортонормированной, если
 Лемма 1. Любой ортонормированный набор векторов евклидова пространства Е всегда линейно не зависим. Доказательство. ◄Пусть - ортонормированный набор векторов евклидова пространства Е. Составим их линейную комбинацию: Умножим скалярно на
Лемма 1. Любой ортонормированный набор векторов евклидова пространства Е всегда линейно не зависим. Доказательство. ◄Пусть - ортонормированный набор векторов евклидова пространства Е. Составим их линейную комбинацию: Умножим скалярно на
 Так как , то получим Тогда αk = 0 для k=1, 2, …, n (в силу произвольности выбора вектора ). Следовательно, векторы линейно независимы. ►
Так как , то получим Тогда αk = 0 для k=1, 2, …, n (в силу произвольности выбора вектора ). Следовательно, векторы линейно независимы. ►
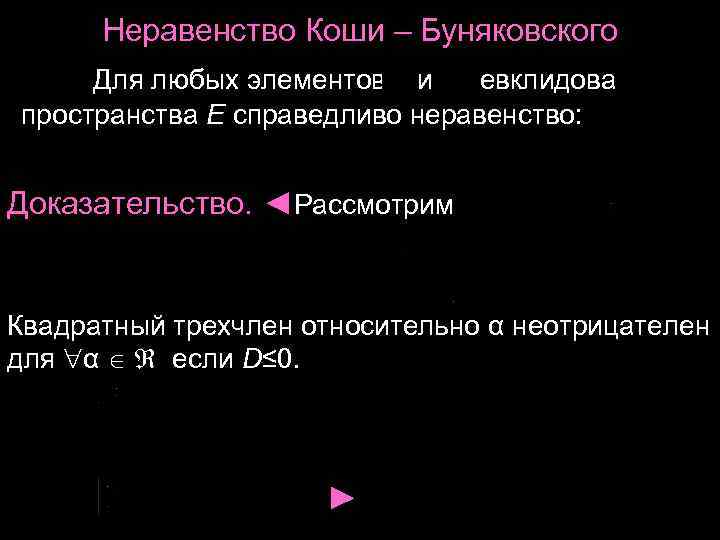
 Неравенство Коши – Буняковского Для любых элементов и евклидова пространства E справедливо неравенство: Доказательство. ◄Рассмотрим Квадратный трехчлен относительно α неотрицателен для α если D≤ 0. ►
Неравенство Коши – Буняковского Для любых элементов и евклидова пространства E справедливо неравенство: Доказательство. ◄Рассмотрим Квадратный трехчлен относительно α неотрицателен для α если D≤ 0. ►
 Неравенство Минковского Для любых элементов и евклидова пространства E справедливо неравенство: Доказательство. ◄ ►
Неравенство Минковского Для любых элементов и евклидова пространства E справедливо неравенство: Доказательство. ◄ ►
 Определение. Углом между ненулевыми элементами называется угол φ, косинус которого: Замечания. 1. Определение корректно, так как согласно неравенству Коши-Буняковского: 2. Если то векторы ортогональны. 3. Нулевой вектор ортогонален любому вектору.
Определение. Углом между ненулевыми элементами называется угол φ, косинус которого: Замечания. 1. Определение корректно, так как согласно неравенству Коши-Буняковского: 2. Если то векторы ортогональны. 3. Нулевой вектор ортогонален любому вектору.
 Определение. Ортонормированным базисом в n мерном евклидовом пространстве называется любая ортонормированная система из n элементов. Замечание. Данное определение корректно, так как по лемме 1 любой ортонормированный набор векторов евклидова пространства Е всегда линейно не зависим, а в n- мерном пространстве любая система, состоящая из n линейно независимых векторов, образует базис.
Определение. Ортонормированным базисом в n мерном евклидовом пространстве называется любая ортонормированная система из n элементов. Замечание. Данное определение корректно, так как по лемме 1 любой ортонормированный набор векторов евклидова пространства Е всегда линейно не зависим, а в n- мерном пространстве любая система, состоящая из n линейно независимых векторов, образует базис.
 Ортогонализация системы векторов в евклидовом пространстве. Теорема. В любом n-мерном евклидовом пространстве En существует ортонормированный базис. Доказательство. ◄Пусть – произвольный базис n- мерного евклидова пространства En. Покажем, что существует ортогональный базис такой, что векторы линейно выражаются через векторы 1. Положим, Очевидно, что 2. Вектор будем искать в виде линейной комбинации векторов
Ортогонализация системы векторов в евклидовом пространстве. Теорема. В любом n-мерном евклидовом пространстве En существует ортонормированный базис. Доказательство. ◄Пусть – произвольный базис n- мерного евклидова пространства En. Покажем, что существует ортогональный базис такой, что векторы линейно выражаются через векторы 1. Положим, Очевидно, что 2. Вектор будем искать в виде линейной комбинации векторов
 Так как векторы линейно независимы (базисные векторы), то Коэффициент с21 найдем из условия 3. Вектор будем искать в виде линейной комбинации векторов Так как векторы линейно независимы (базисные векторы), то Коэффициенты с31 и с32 найдем из условий:
Так как векторы линейно независимы (базисные векторы), то Коэффициент с21 найдем из условия 3. Вектор будем искать в виде линейной комбинации векторов Так как векторы линейно независимы (базисные векторы), то Коэффициенты с31 и с32 найдем из условий:
 Следовательно,
Следовательно,
 Пусть векторы уже построены. Тогда вектор ищем в виде Вектор , так как в противном случае вектор был бы линейной комбинацией базисных векторов что невозможно в силу линейной независимости базисных векторов. Коэффициенты сn j найдем из условий:
Пусть векторы уже построены. Тогда вектор ищем в виде Вектор , так как в противном случае вектор был бы линейной комбинацией базисных векторов что невозможно в силу линейной независимости базисных векторов. Коэффициенты сn j найдем из условий:
 Таким образом, система векторов ортогональная система. Нормируем ее. Пусть Тогда ортонормированная система векторов. По лемме 1 они образуют базис в Приведенный алгоритм построения О. Н. Б. называется процессом ортогонализации. ►
Таким образом, система векторов ортогональная система. Нормируем ее. Пусть Тогда ортонормированная система векторов. По лемме 1 они образуют базис в Приведенный алгоритм построения О. Н. Б. называется процессом ортогонализации. ►
 Свойства О. Н. Б. Пусть О. Н. Б. евклидова пространства En. Тогда Доказательство.
Свойства О. Н. Б. Пусть О. Н. Б. евклидова пространства En. Тогда Доказательство.
 Доказательство.
Доказательство.
 Определение. Множество векторов, ортогональных данному вектору является подпространством евклидова пространства E и называется ортогональным дополнением к вектору . Определение. Пусть W - подпространство евклидова пространства E. Совокупность всех элементов пространства E, таких что , называется ортогональным дополнением подпространства W.
Определение. Множество векторов, ортогональных данному вектору является подпространством евклидова пространства E и называется ортогональным дополнением к вектору . Определение. Пусть W - подпространство евклидова пространства E. Совокупность всех элементов пространства E, таких что , называется ортогональным дополнением подпространства W.
 Сопряженные линейные операторы в евклидовом пространстве. Пусть E – евклидово пространство. Определение. Оператор A* называется сопряженным к линейному оператору : E→E, если Замечание. A* - линейный оператор. Доказательство. ◄Если оператор A* - линейный , то Из определения сопряженного оператора:
Сопряженные линейные операторы в евклидовом пространстве. Пусть E – евклидово пространство. Определение. Оператор A* называется сопряженным к линейному оператору : E→E, если Замечание. A* - линейный оператор. Доказательство. ◄Если оператор A* - линейный , то Из определения сопряженного оператора:
 Из свойств скалярного произведения: Данное равенство верно для любого A* - линейный. ►
Из свойств скалярного произведения: Данное равенство верно для любого A* - линейный. ►
 Утверждение. Пусть : E→E – линейный оператор, A* − сопряженный оператор. Матрица сопряженного оператора в любом ортонормированном базисе является транспонированной к матрице A, т. е. A*=At Доказательство. ◄
Утверждение. Пусть : E→E – линейный оператор, A* − сопряженный оператор. Матрица сопряженного оператора в любом ортонормированном базисе является транспонированной к матрице A, т. е. A*=At Доказательство. ◄
 (так как базис ортонормированный) Тогда ►
(так как базис ортонормированный) Тогда ►
![> Примеры. 2)Рассмотрим - множество функций бесконечно дифференцируемых на [0, 1], > Примеры. 2)Рассмотрим - множество функций бесконечно дифференцируемых на [0, 1],](https://present5.com/presentation/3/173142797_132636254.pdf-img/173142797_132636254.pdf-96.jpg) Примеры. 2)Рассмотрим - множество функций бесконечно дифференцируемых на [0, 1], у которых в точках 0 и 1 значения функций и значения производных любого порядка равны 0, то есть
Примеры. 2)Рассмотрим - множество функций бесконечно дифференцируемых на [0, 1], у которых в точках 0 и 1 значения функций и значения производных любого порядка равны 0, то есть
 Оператор - оператор дифференцирования: Тогда
Оператор - оператор дифференцирования: Тогда
 Свойства сопряженного оператора. 5) У каждого л. о. существует ровно один сопряженный ему оператор. 6) Если матрица л. о. невырожденная, то
Свойства сопряженного оператора. 5) У каждого л. о. существует ровно один сопряженный ему оператор. 6) Если матрица л. о. невырожденная, то
 Самосопряженные линейные операторы в евклидовом пространстве. Определение. Оператор : E→E называется самосопряженным, если , то есть Примеры. 1. Тождественный оператор является самосопряженным: 2. Нулевой оператор является самосопряженным:
Самосопряженные линейные операторы в евклидовом пространстве. Определение. Оператор : E→E называется самосопряженным, если , то есть Примеры. 1. Тождественный оператор является самосопряженным: 2. Нулевой оператор является самосопряженным:
 – самосопряженный линейный оператор.
– самосопряженный линейный оператор.

