Линейные дифференциальные уравнения второго порядка Лекция 19

Линейные дифференциальные уравнения второго порядка Лекция № 19 1

Линейные дифференциальные уравнения 2 -го порядка Линейным дифф. уравнением 2 -го порядка называется уравнение вида y`` + p(x) y` + q(x) y = f(x), где у - искомая функция, p(x), q(x) и f(x) - функции, непрерывные на некотором (a, b). Если f(x) = 0, ур-е называется линейным однородным, в противном случае линейным неоднородным уравнением. 2

Линейные однородные уравнения 2 -го порядка Рассмотрим свойства решений линейных однородных диф. уравнений 2 -го порядка y``+ p(x) y`+ q(x) y = 0. Теорема 1. Пусть функции у1(х) и у2(х) решения этого уравнения. Тогда функция у = С 1 у1(х) + С 2 у2(х) также является решением этого уравнения при любых постоянных С 1 и С 2. Доказательство: подстановкой указанной функции в диф. ур-е. 3

Определение. Функции у1(х) и у2(х) называются линейно зависимыми на (a, b), если можно найти такие числа 1 и 2, не равные нулю одновременно, что для х (a, b) выполняется равенство 1 у1(х) + 2 у2(х) = 0. В этом случае у1(х) и у2(х) пропорциональны. Обратное утверждение также верно: если две функции пропорциональны на (a, b), то они линейно зависимы. Если нельзя найти двух одновременно 0 чисел 1 и 2, то функции называются линейно независимыми на (a, b). 4

Введем понятие определителя Вронского: Теорема 2. Если функции у1(х) и у2(х) линейно зависимы на интервале (a, b), то определитель Вронского, составленный из них, равен 0 на этом интервале; если же функции линейно независимы на (a, b), то определитель Вронского 0 на (a, b). Доказательство: Пусть у1 и у2 линейно зависимы на (a, b) y 1 = ky 2 y 1`= k y 2` 5

в определителе W(x) будут пропорциональны столбцы W(x)=0 на (a, b). Ч. т. д. Теорема 3. Пусть решения диф. уравнения у1(х) и у2(х) линейно независимы на (a, b). Тогда функция у(х) = С 1 у1(х) + С 2 у2(х), где С 1 и С 2 - произвольные постоянные, является общим решением однородного линейного диф. уравнения 2 -го порядка. 6

Линейные неоднородные уравнения второго порядка Теорема. Общее решение уравнения y``+ p(x) y`+ q(x) y = f(x) состоит из суммы его частного решения и общего решения соответствующего однородного уравнения: y(x) = Y(x) + y*(x). Доказательство: Пусть Y(x) - решение соответствующего однородного уравнения. Подставим разность y(x) - Y(x) в неоднородное диф. уравнение 7

[y - Y]``+ p(x) [y - Y]` + q(x)[y - Y] = =[y``+ p(x)y`+ q(x)y] - [Y ``+p(x)Y `+ q(x)Y]= = f(x) - f(x) = 0 y - Y(x) = C 10 y 1(x) + C 20 y 2(x) - частное решение диф. уравнения. Теорема доказана. Эта теорема указывает способ нахождения неоднородного диф. уравнения: нужно найти общее решение соответствующего однородного диф. уравнения и какое-либо частное решение неоднородного уравнения. 8

Частное решение можно найти методом вариации произвольных постоянных С 1 и С 2: Вначале находят общее решение однородного диф. уравнения Y = C 1(x) y 1(x) + C 2(x) y 2(x). C 1(x) и С 2(х) можно найти, решив систему затем проинтегрировав С 1`(x) и С 2`(x). 9

Линейные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами Пусть функции p(x) и q(x) – постоянные величины. Тогда диф. уравнение называется линейным уравнением с постоянными коэффициентами. Линейное однородное уравнение с постоянными коэффициентами y``+ p y` + q y = 0. Будем искать решение этого уравнения в виде y = ekx (k – некоторое число). 10

Подставим эту функцию в уравнение: k 2 ekx + pk ekx + q ekx = 0. Сократим обе части равенства на ekx, получим k 2 + p k + q = 0. Это уравнение называется характеристическим уравнением. k является корнем этого уравнения. Вид решение зависит от того, какие корни имеет характеристическое уравнение. 11

12

Доказательство: Достаточно убедиться в том, что каждое из слагаемых в правых частях является решением диф. ур-я, а затем по определителю Вронского удостовериться в том, что каждая пара функций в этих равенствах линейно независима. 13

Пример 1. y`` - 5 y` + 4 y = 0. Характеристическое уравнение данного диф. уравнения имеет вид k 2 - 5 k + 4 = 0. Его корни вещественны и различны: k 1 = 1 и k 2 = 4. Общее решение данного диф. уравнения y = C 1 ex + C 2 e 4 x. 14

Пример 2. y`` - 6 y` + 9 y = 0. Составим характеристическое уравнение k 2 - 6 k + 9 = 0, (k - 3)2 = 0. Оно имеет кратный корень k = 3. Общее решение имеет вид y = e 3 x(C 1 + C 2 x). 15

Пример 3. y``- 2 y` + 2 = 0. Характеристическое уравнение k 2 -2 k+2=0 не имеет вещественных корней. a = -1, b = 1. Общее решение диф. уравнения y = e-x (C 1 sinx + C 2 cosx). 16

Пример 4. Решить неоднородное уравнение y`` - 3 y` + 2 y = ex. Вначале решим соответствующее однородное уравнение y`` - 3 y` + 2 y = 0. Характеристическое уравнение k 2 - 3 k + 2 = 0, корни этого уравнения k 1 = 1 и k 2 = 2. Общее решение однородного уравнения y = C 1 y 1(x) + C 2 y 1(x) = C 1 ex + C 2 e 2 x. Полагаем теперь, что С 1 и С 2 - функции переменной х: 17

y = C 1(x) ex + C 2(x) e 2 x (1) - в таком виде будем искать решение данного диф. уравнения. С 1(х) и С 2(х) найдем методом вариации произвольных постоянных. Найдем первые производные этих функций, решая систему: 18

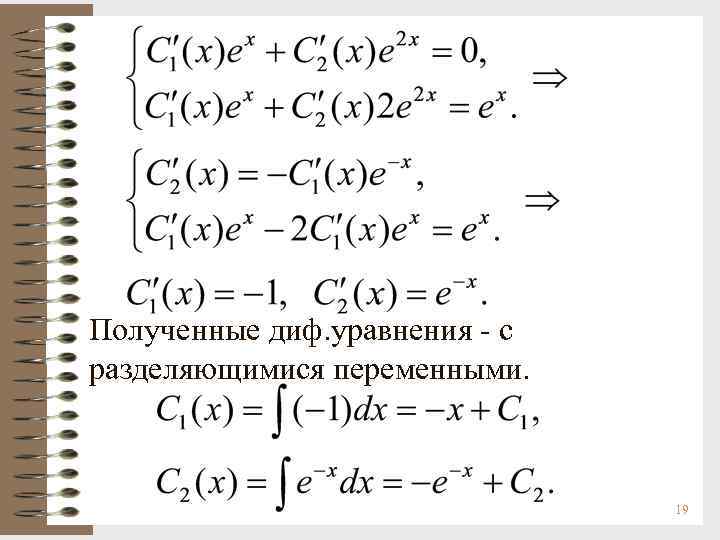Полученные диф. уравнения - с разделяющимися переменными. 19

Подставим найденные С 1(х) и С 2(х) в формулу (1), получим общее решение исходного неоднородного диф. уравнения: y = (-x + C 1) ex + (-e-x + C 2) e 2 x = = C 1 ex + C 2 e 2 x + (-x - 1) ex. Обратите внимание на структуру полученного решения: Здесь Y(x) = C 1 ex + C 2 e 2 x - общее решение однородного уравнения, y*(x) = (-x - 1) ex - частное решение неоднородного диф. уравнения. y = Y(x) + y*(x). 20