lin_ur_1poryadka.ppt
- Количество слайдов: 60
 Линейные дифференциальные уравнения 1 - го порядка Лекция
Линейные дифференциальные уравнения 1 - го порядка Лекция
 Линейные уравнения первого порядка Определение Линейное дифференциальное уравнение первого порядка - ДУ 1 -го порядка, линейное относительно неизвестной функции y и ее производной y . В общем случае линейное уравнение 1 -го порядка можно записать в виде y + p(x) y = f(x) , где p(x) , f(x) – заданные непрерывные функции. Ø Ø Определение Если f(x) ≡ 0 , то линейное уравнение y + p(x) y = 0 называется однородным. В противном случае уравнение называется неоднородным.
Линейные уравнения первого порядка Определение Линейное дифференциальное уравнение первого порядка - ДУ 1 -го порядка, линейное относительно неизвестной функции y и ее производной y . В общем случае линейное уравнение 1 -го порядка можно записать в виде y + p(x) y = f(x) , где p(x) , f(x) – заданные непрерывные функции. Ø Ø Определение Если f(x) ≡ 0 , то линейное уравнение y + p(x) y = 0 называется однородным. В противном случае уравнение называется неоднородным.
 Линейное однородное уравнение y + p(x) y = 0 является уравнением с разделяющимися переменными. Его общее решение:
Линейное однородное уравнение y + p(x) y = 0 является уравнением с разделяющимися переменными. Его общее решение:

 Пример
Пример
 Пример
Пример
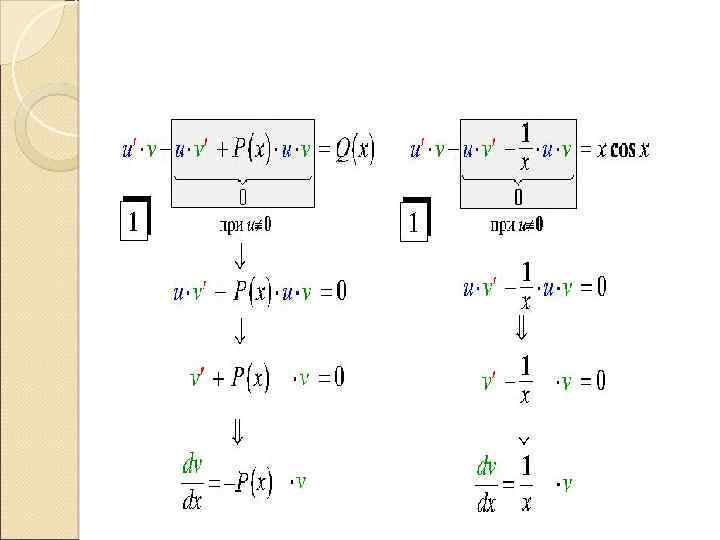


 Пример
Пример

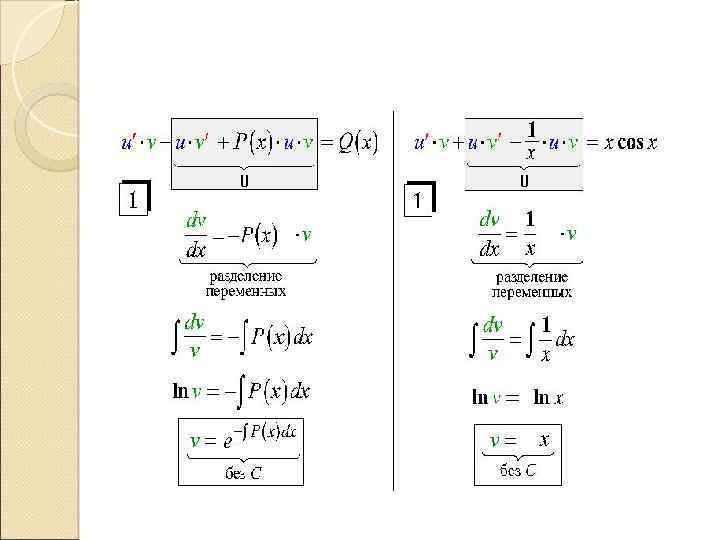
 Метод вариации постоянной (метод Лагранжа) y + p(x) y = f(x) 1)Интегрируем однородное уравнение y + p(x) y = 0, Соответствующее данному неоднородному уравнению. Его общее решение имеет вид : 2) Полагаем, что решение неоднородного уравнения Функцию C(x) найдем, подставив y и y в исходное неоднородное уравнение.
Метод вариации постоянной (метод Лагранжа) y + p(x) y = f(x) 1)Интегрируем однородное уравнение y + p(x) y = 0, Соответствующее данному неоднородному уравнению. Его общее решение имеет вид : 2) Полагаем, что решение неоднородного уравнения Функцию C(x) найдем, подставив y и y в исходное неоднородное уравнение.
 Получим: Таким образом, общее решение линейного неоднородного уравнения имеет вид: q Замечания. Раскроем скобки
Получим: Таким образом, общее решение линейного неоднородного уравнения имеет вид: q Замечания. Раскроем скобки
 Уравнения в полных дифференциалах
Уравнения в полных дифференциалах
 ТЕОРЕМА Пусть функции M(x , y) , N(x , y) определены и непрерывны в области D и имеют в ней непрерывные частные производные Для того чтобы выражение M(x , y)dx + N(x , y)dy представляло собой полный дифференциал некоторой функции u(x , y) , необходимо и достаточно, чтобы во всех точках области D выполнялось условие
ТЕОРЕМА Пусть функции M(x , y) , N(x , y) определены и непрерывны в области D и имеют в ней непрерывные частные производные Для того чтобы выражение M(x , y)dx + N(x , y)dy представляло собой полный дифференциал некоторой функции u(x , y) , необходимо и достаточно, чтобы во всех точках области D выполнялось условие
 Способы нахождения функции u(x , y): 1) используя одну из следующих формул: где (x 0 , y 0) – любая точка области D непрерывности функций M(x , y), N(x , y).
Способы нахождения функции u(x , y): 1) используя одну из следующих формул: где (x 0 , y 0) – любая точка области D непрерывности функций M(x , y), N(x , y).
 Метод интегрируемых комбинаций. Суть метода интегрируемых комбинаций: выделить в M(x , y)dx + N(x , y)dy выражения, являющиеся дифференциалами известных функций ( «интегрируемые комбинации» ) и привести его таким образом к виду du(x , y). ПРИМЕРЫ интегрируемых комбинаций:
Метод интегрируемых комбинаций. Суть метода интегрируемых комбинаций: выделить в M(x , y)dx + N(x , y)dy выражения, являющиеся дифференциалами известных функций ( «интегрируемые комбинации» ) и привести его таким образом к виду du(x , y). ПРИМЕРЫ интегрируемых комбинаций:
 Интегрирующий множитель Определение Функция m(x, y) называется интегрирующим множителем уравнения M(x , y)dx + N(x , y)dy = 0, если после его умножения на m(x, y) левая часть уравнения становится полным дифференциалом некоторой функции. Ø Пусть функции M(x , y) , N(x , y) определены и непрерывны в области D плоскости x. Oy и имеют в ней непрерывные частные производные
Интегрирующий множитель Определение Функция m(x, y) называется интегрирующим множителем уравнения M(x , y)dx + N(x , y)dy = 0, если после его умножения на m(x, y) левая часть уравнения становится полным дифференциалом некоторой функции. Ø Пусть функции M(x , y) , N(x , y) определены и непрерывны в области D плоскости x. Oy и имеют в ней непрерывные частные производные
 ТЕОРЕМА (о существовании интегрирующего множителя вида m(x) или m(y)). Пусть 1) Если = (x), то уравнение имеет
ТЕОРЕМА (о существовании интегрирующего множителя вида m(x) или m(y)). Пусть 1) Если = (x), то уравнение имеет
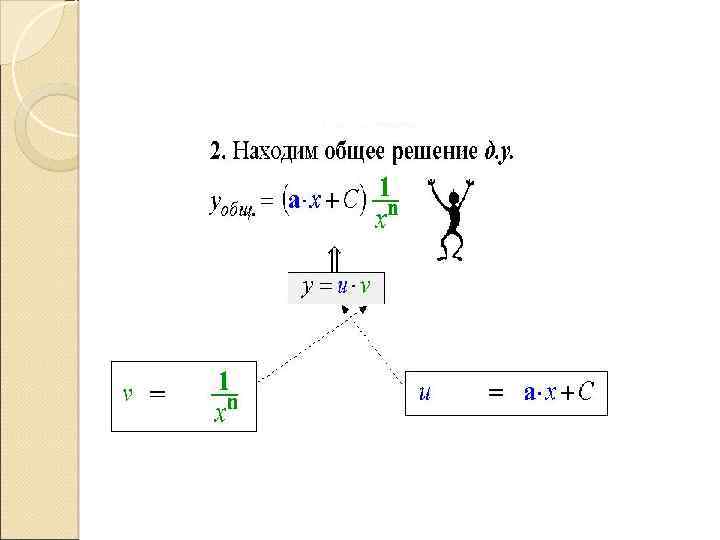
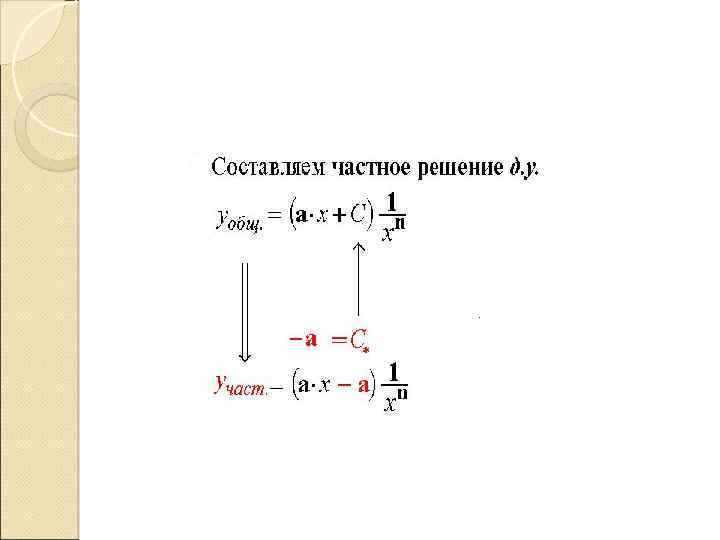
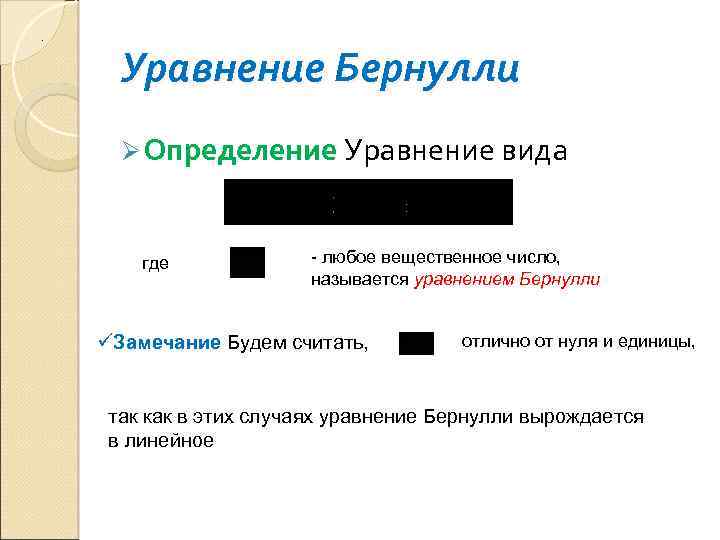 . Уравнение Бернулли Ø Определение Уравнение вида где - любое вещественное число, называется уравнением Бернулли üЗамечание Будем считать, отлично от нуля и единицы, так как в этих случаях уравнение Бернулли вырождается в линейное
. Уравнение Бернулли Ø Определение Уравнение вида где - любое вещественное число, называется уравнением Бернулли üЗамечание Будем считать, отлично от нуля и единицы, так как в этих случаях уравнение Бернулли вырождается в линейное
 Уравнение Бернулли всегда может быть сведено к линейному уравнению заменой деля уравнение на ü Замечание Особым решением Если может быть лишь при частное решение, особое решение.
Уравнение Бернулли всегда может быть сведено к линейному уравнению заменой деля уравнение на ü Замечание Особым решением Если может быть лишь при частное решение, особое решение.
 2) Решив получившееся после замены линейное уравнение методом Бернулли, получим: z = u(x) v(x) , Таким образом, решение уравнения Бернулли можно сразу искать в виде произведения двух функций методом Бернулли, не приводя предварительно к линейному уравнению.
2) Решив получившееся после замены линейное уравнение методом Бернулли, получим: z = u(x) v(x) , Таким образом, решение уравнения Бернулли можно сразу искать в виде произведения двух функций методом Бернулли, не приводя предварительно к линейному уравнению.
 Дифференциальные уравнения высшего порядка Ø Определение Сведение уравнение более высокого порядка к уравнению порядком ниже называется понижением порядка. Рассмотрим некоторые случаи, в которых данное дифференциальное уравнений высшего порядка может быть упрощено понижением его порядка.
Дифференциальные уравнения высшего порядка Ø Определение Сведение уравнение более высокого порядка к уравнению порядком ниже называется понижением порядка. Рассмотрим некоторые случаи, в которых данное дифференциальное уравнений высшего порядка может быть упрощено понижением его порядка.
 Определение Дифференциальными уравнениями высшего порядка называют уравнения порядка выше первого. В общем случае ДУ высшего порядка имеет вид F(x, y , … , y(n)) = 0 , где n > 1. ü Замечание Функция F может и не зависеть от некоторых из аргументов x, y , … , y(n– 1). Ø ü Определение ДУ высшего порядка, которое можно записать в виде: y(n) = f(x, y , … , y(n– 1)) , называют уравнением, разрешенным относительно старшей производной.
Определение Дифференциальными уравнениями высшего порядка называют уравнения порядка выше первого. В общем случае ДУ высшего порядка имеет вид F(x, y , … , y(n)) = 0 , где n > 1. ü Замечание Функция F может и не зависеть от некоторых из аргументов x, y , … , y(n– 1). Ø ü Определение ДУ высшего порядка, которое можно записать в виде: y(n) = f(x, y , … , y(n– 1)) , называют уравнением, разрешенным относительно старшей производной.
 Дифференциальные уравнения 1 -го порядка, не разрешенные относительно производной ДУ 1 -го порядка, разрешенное относительно производной – уравнение, которое можно записать в виде y = f(x, y). В общем случае ДУ 1 -го порядка имеет вид: F(x, y, y ) = 0. Если из уравнения F(x, y, y ) = 0 нельзя выразить y , то уравнение называют не разрешенным относительно производной.
Дифференциальные уравнения 1 -го порядка, не разрешенные относительно производной ДУ 1 -го порядка, разрешенное относительно производной – уравнение, которое можно записать в виде y = f(x, y). В общем случае ДУ 1 -го порядка имеет вид: F(x, y, y ) = 0. Если из уравнения F(x, y, y ) = 0 нельзя выразить y , то уравнение называют не разрешенным относительно производной.
 Уравнения, разрешаемые относительно y неоднозначно Пусть F(x, y, y ) = 0 таково, что его можно разрешить относительно y неоднозначно. Т. е. уравнение F(x, y, y ) = 0 эквивалентно k различным уравнениям y = f 1(x, y) , y = f 2(x, y) , y = f 3(x, y) , … , y = fk(x, y). Предположим, что для каждого из уравнений найден общий интеграл: Φ 1(x , y , C) = 0 , Φ 2(x , y , C) = 0 , …. , Φk(x , y , C) = 0. Совокупность общих интегралов называется общим интегралом уравнения разрешаемого относительно y неоднозначно.
Уравнения, разрешаемые относительно y неоднозначно Пусть F(x, y, y ) = 0 таково, что его можно разрешить относительно y неоднозначно. Т. е. уравнение F(x, y, y ) = 0 эквивалентно k различным уравнениям y = f 1(x, y) , y = f 2(x, y) , y = f 3(x, y) , … , y = fk(x, y). Предположим, что для каждого из уравнений найден общий интеграл: Φ 1(x , y , C) = 0 , Φ 2(x , y , C) = 0 , …. , Φk(x , y , C) = 0. Совокупность общих интегралов называется общим интегралом уравнения разрешаемого относительно y неоднозначно.
 Замечания Если уравнение ü F(x, y, y ) = 0 разрешается относительно y неоднозначно, то через каждую точку M 0(x 0 , y 0) области, будет проходить в общем случае k интегральных кривых. Однако условие единственности для этой точки будет считаться нарушенным только в том случае, когда хотя бы две кривые в точке M 0 будут иметь общую касательную.
Замечания Если уравнение ü F(x, y, y ) = 0 разрешается относительно y неоднозначно, то через каждую точку M 0(x 0 , y 0) области, будет проходить в общем случае k интегральных кривых. Однако условие единственности для этой точки будет считаться нарушенным только в том случае, когда хотя бы две кривые в точке M 0 будут иметь общую касательную.
 ПРИМЕР Найти общий интеграл уравнения (y )2 – 4 x 2 = 0. Найти решение, удовлетворяющее условию а) y(1) = 1 , б) y(0) = 0.
ПРИМЕР Найти общий интеграл уравнения (y )2 – 4 x 2 = 0. Найти решение, удовлетворяющее условию а) y(1) = 1 , б) y(0) = 0.
 ДУ порядка n имеет множество решений (интегралов). Чтобы выбрать одно из них, задают n условий, которым должно удовлетворять искомое решение. Обычно, задают значение искомой функции и всех ее производных до порядка n – 1 включительно при некотором значении аргумента x = x 0 : y(x 0)=y 0 , y (x 0) =y 01, y (x 0)= y 02 , …, y(n– 1)(x 0)=y 0 n– 1. Совокупность этих условий называется начальными условиями для дифференциального уравнения n-го порядка. Ø Определение Нахождение решения уравнения, удовлетворяющего заданным начальным условиям , называется решением задачи Коши для этого уравнения.
ДУ порядка n имеет множество решений (интегралов). Чтобы выбрать одно из них, задают n условий, которым должно удовлетворять искомое решение. Обычно, задают значение искомой функции и всех ее производных до порядка n – 1 включительно при некотором значении аргумента x = x 0 : y(x 0)=y 0 , y (x 0) =y 01, y (x 0)= y 02 , …, y(n– 1)(x 0)=y 0 n– 1. Совокупность этих условий называется начальными условиями для дифференциального уравнения n-го порядка. Ø Определение Нахождение решения уравнения, удовлетворяющего заданным начальным условиям , называется решением задачи Коши для этого уравнения.
 ü Замечание Единственность решения задачи Коши для уравнения n-го порядка (n > 1) НЕ ОЗНАЧАЕТ, что через данную точку M 0(x 0 , y 0) плоскости x. Oy проходит одна интегральная кривая y = (x). Кривых через точку M 0 проходит множество, а единственность означает, что они различаются набором значений y (x 0) , …, y(n– 1)(x 0). Из теоремы 1 1) ДУ имеет множество решений. 2) Совокупность решений зависит от n произвольных постоянных.
ü Замечание Единственность решения задачи Коши для уравнения n-го порядка (n > 1) НЕ ОЗНАЧАЕТ, что через данную точку M 0(x 0 , y 0) плоскости x. Oy проходит одна интегральная кривая y = (x). Кривых через точку M 0 проходит множество, а единственность означает, что они различаются набором значений y (x 0) , …, y(n– 1)(x 0). Из теоремы 1 1) ДУ имеет множество решений. 2) Совокупность решений зависит от n произвольных постоянных.
 ОПРЕДЕЛЕНИЕ. Общим решением дифференциального уравнения y(n) = f(x, y, y , … , y(n– 1)) в области D существования и единственности решения задачи Коши называется функция y = (x , C 1 , C 2 , … , Cn) , зависящая от x и n произвольных постоянных C 1 , C 2 , … , Cn , которая удовлетворяет следующим двум условиям: 1) при любых допустимых значениях C 1 , C 2 , … , Cn она удовлетворяет уравнению 2) каковы бы ни были начальные условия y(x 0) = y 0, y (x 0) = y 01, y (x 0) = y 02, … , y(n– 1)(x 0) = y 0 n– (где (x 0, y 01, y 02, …, y 0 n– 1) D), можно найти единственный набор значений C 1 = C 01 , C 2 = C 02 , … , Cn = C 0 n такой, что функция y = (x , C 01 , C 02 , … , C 0 n) удовлетворяет заданным начальным условиям. Ø
ОПРЕДЕЛЕНИЕ. Общим решением дифференциального уравнения y(n) = f(x, y, y , … , y(n– 1)) в области D существования и единственности решения задачи Коши называется функция y = (x , C 1 , C 2 , … , Cn) , зависящая от x и n произвольных постоянных C 1 , C 2 , … , Cn , которая удовлетворяет следующим двум условиям: 1) при любых допустимых значениях C 1 , C 2 , … , Cn она удовлетворяет уравнению 2) каковы бы ни были начальные условия y(x 0) = y 0, y (x 0) = y 01, y (x 0) = y 02, … , y(n– 1)(x 0) = y 0 n– (где (x 0, y 01, y 02, …, y 0 n– 1) D), можно найти единственный набор значений C 1 = C 01 , C 2 = C 02 , … , Cn = C 0 n такой, что функция y = (x , C 01 , C 02 , … , C 0 n) удовлетворяет заданным начальным условиям. Ø

 Уравнение Φ(x , y , C 1 , C 2 , … , Cn) = 0 , задающее общее решение в неявном виде, называется общим интегралом уравнения. С геометрической точки зрения общее решение (общий интеграл) дифференциального уравнения представляет собой семейство интегральных кривых, зависящих от n параметров. Решение , в каждой точке которого выполняется условие единственности, называется частным. Любое решение , получающееся из общего решения (интеграла) при конкретных значениях постоянных Ci (включая Ci = ), является частным. Решение , в каждой точке которого нарушено условие единственности, называется особым. Особое решение, не входит в общее решение дифференциального уравнения.
Уравнение Φ(x , y , C 1 , C 2 , … , Cn) = 0 , задающее общее решение в неявном виде, называется общим интегралом уравнения. С геометрической точки зрения общее решение (общий интеграл) дифференциального уравнения представляет собой семейство интегральных кривых, зависящих от n параметров. Решение , в каждой точке которого выполняется условие единственности, называется частным. Любое решение , получающееся из общего решения (интеграла) при конкретных значениях постоянных Ci (включая Ci = ), является частным. Решение , в каждой точке которого нарушено условие единственности, называется особым. Особое решение, не входит в общее решение дифференциального уравнения.
 ТЕОРЕМА (Коши). Пусть для уравнения y(n) = f(x, y , … , y(n– 1)) выполняются два условия: 1) функция f(x, y , … , y(n– 1)) непрерывна как функция (n + 1)-ой переменной x, y , … , y(n– 1) 2) функция f(x, y , … , y(n– 1)) имеет в этой
ТЕОРЕМА (Коши). Пусть для уравнения y(n) = f(x, y , … , y(n– 1)) выполняются два условия: 1) функция f(x, y , … , y(n– 1)) непрерывна как функция (n + 1)-ой переменной x, y , … , y(n– 1) 2) функция f(x, y , … , y(n– 1)) имеет в этой
 Дифференциальные уравнения 2 порядка
Дифференциальные уравнения 2 порядка

 Дифференциальные уравнения n-го порядка Простейшее дифференциальное уравнение n-го порядка – уравнение вида - легко интегрируется в квадратурах. Решение уравнения находится кратным интегрированием. интегрируя , получим общее решение
Дифференциальные уравнения n-го порядка Простейшее дифференциальное уравнение n-го порядка – уравнение вида - легко интегрируется в квадратурах. Решение уравнения находится кратным интегрированием. интегрируя , получим общее решение
 Пример Найти общее решение уравнения и частное решение, удовлетворяющее краевым условиям: Решение общее решение частное решение
Пример Найти общее решение уравнения и частное решение, удовлетворяющее краевым условиям: Решение общее решение частное решение
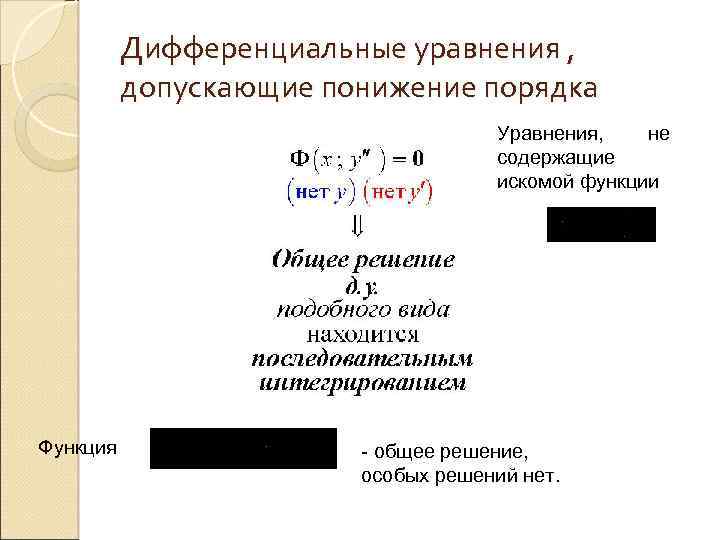 Дифференциальные уравнения , допускающие понижение порядка Уравнения, не содержащие искомой функции Функция - общее решение, особых решений нет.
Дифференциальные уравнения , допускающие понижение порядка Уравнения, не содержащие искомой функции Функция - общее решение, особых решений нет.
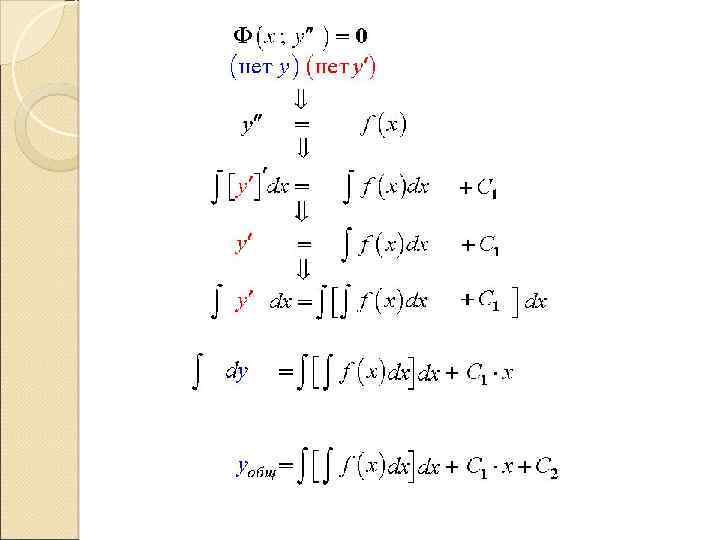
 Пример
Пример
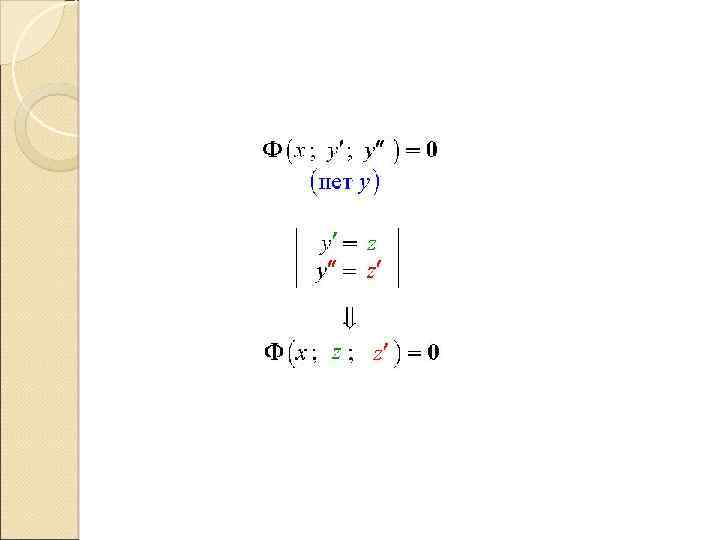
 Пример
Пример
 Пример
Пример

 Уравнения, не содержащие независимой переменной Обратимся к перевернутому уравнению Разделим на , интегрируя, получим общее решение Рассмотрим то прямая Если оно имеет решение вида решение, частное или особое
Уравнения, не содержащие независимой переменной Обратимся к перевернутому уравнению Разделим на , интегрируя, получим общее решение Рассмотрим то прямая Если оно имеет решение вида решение, частное или особое
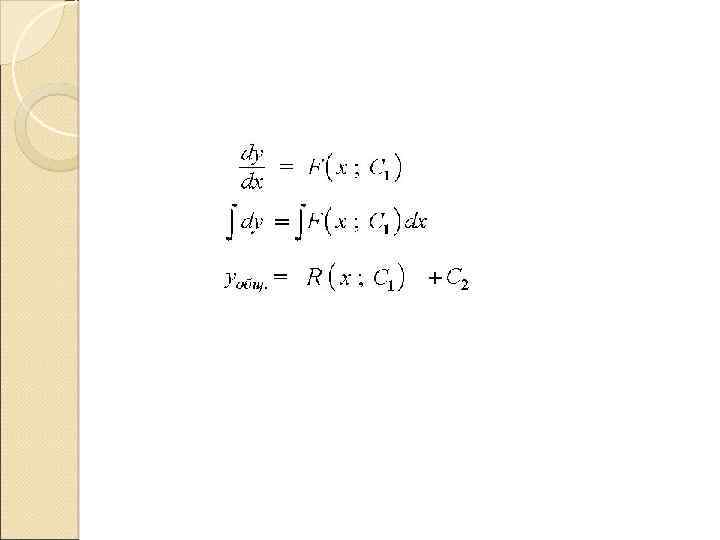
 Уравнения, не содержащие искомой функции Пусть ДУ имеет вид F(x, y ) = 0 , Возможны 2 случая: 1) разрешимо относительно y неоднозначно; 2)неразрешимо относительно y , но допускает параметрическое представление, т. е. может быть заменено двумя урав нениями вида x = (t) , y = (t). Тогда решения уравнения могут быть найдены в параметрическом виде. Имеем: dy = y dx , x = (t) dx = dt , dy = (t) dt ,
Уравнения, не содержащие искомой функции Пусть ДУ имеет вид F(x, y ) = 0 , Возможны 2 случая: 1) разрешимо относительно y неоднозначно; 2)неразрешимо относительно y , но допускает параметрическое представление, т. е. может быть заменено двумя урав нениями вида x = (t) , y = (t). Тогда решения уравнения могут быть найдены в параметрическом виде. Имеем: dy = y dx , x = (t) dx = dt , dy = (t) dt ,
 Таким образом, интегральные кривые уравнения имеют параметрические уравнения: Замечания 1) Общий интеграл уравнения получается исключением параметра t из системы (если это возможно). 2) Если уравнение можно разрешить относительно x, т. е. записать в виде x = (y ) , то в качестве параметра удобно брать t = y . Тогда общий интеграл уравнения ü
Таким образом, интегральные кривые уравнения имеют параметрические уравнения: Замечания 1) Общий интеграл уравнения получается исключением параметра t из системы (если это возможно). 2) Если уравнение можно разрешить относительно x, т. е. записать в виде x = (y ) , то в качестве параметра удобно брать t = y . Тогда общий интеграл уравнения ü
 Пример
Пример

 Уравнения, содержащее только производную Пусть ДУ имеет вид F(y ) = 0. Тогда y не должна зависеть от x и y, т. е. быть постоянной. Пусть y = ki удовлетворяет уравнению F(y ) = 0. Тогда y = ki x + C , Общий интеграл уравнения будет иметь вид
Уравнения, содержащее только производную Пусть ДУ имеет вид F(y ) = 0. Тогда y не должна зависеть от x и y, т. е. быть постоянной. Пусть y = ki удовлетворяет уравнению F(y ) = 0. Тогда y = ki x + C , Общий интеграл уравнения будет иметь вид

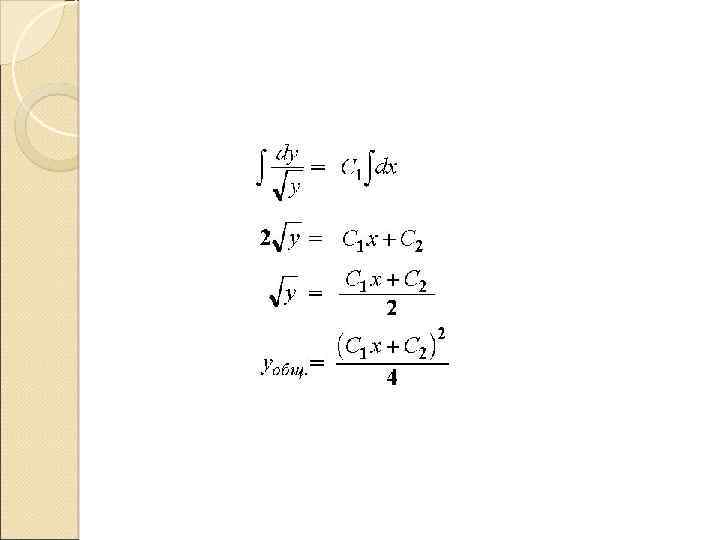
 Уравнение Лагранжа Уравнение F(x, y, y ) = 0 называется уравнением Лагранжа, если оно является линейным относительно x и y, т. е. имеет вид: F 1(y ) x + F 2(y ) y = G(y ). Так как F 2(y ) 0 (иначе это будет неполное уравнение), то уравнение Лагранжа можно записать в виде y = x (y ) + (y ). Общее решение уравнения Лагранжа можно найти в параметрическом виде. Если (y ) ≢ y , то общее решение уравнения будет иметь вид:
Уравнение Лагранжа Уравнение F(x, y, y ) = 0 называется уравнением Лагранжа, если оно является линейным относительно x и y, т. е. имеет вид: F 1(y ) x + F 2(y ) y = G(y ). Так как F 2(y ) 0 (иначе это будет неполное уравнение), то уравнение Лагранжа можно записать в виде y = x (y ) + (y ). Общее решение уравнения Лагранжа можно найти в параметрическом виде. Если (y ) ≢ y , то общее решение уравнения будет иметь вид:
 Уравнение Клеро Пусть в уравнении Лагранжа (y ) ≡ y . В этом случае, уравнение называют уравнением Клеро. Уравнение F(x, y, y ) = 0 называется уравнением Клеро, если оно может быть записано в виде y = x y + (y ). Общее решение уравнения Клеро имеет вид: y = x C + (C). Кроме того, если (t) const , то уравнение Клеро имеет особое решение
Уравнение Клеро Пусть в уравнении Лагранжа (y ) ≡ y . В этом случае, уравнение называют уравнением Клеро. Уравнение F(x, y, y ) = 0 называется уравнением Клеро, если оно может быть записано в виде y = x y + (y ). Общее решение уравнения Клеро имеет вид: y = x C + (C). Кроме того, если (t) const , то уравнение Клеро имеет особое решение


