Линейные цепи переменного тока t
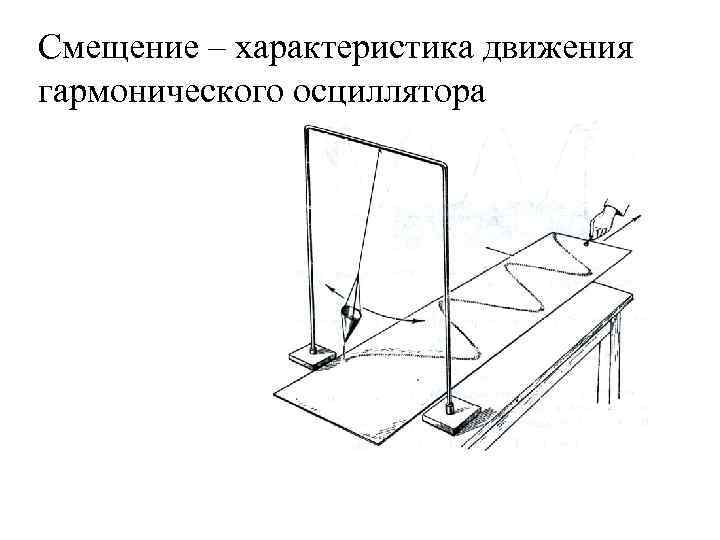Смещение – характеристика движения гармонического осциллятора
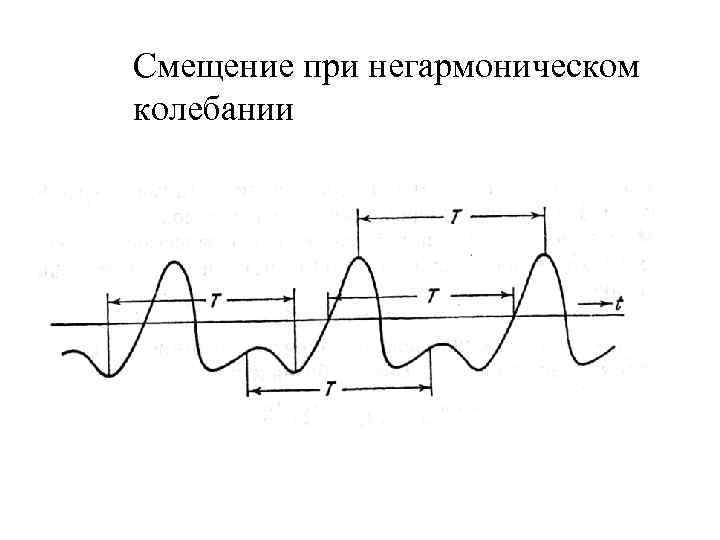Смещение при негармоническом колебании
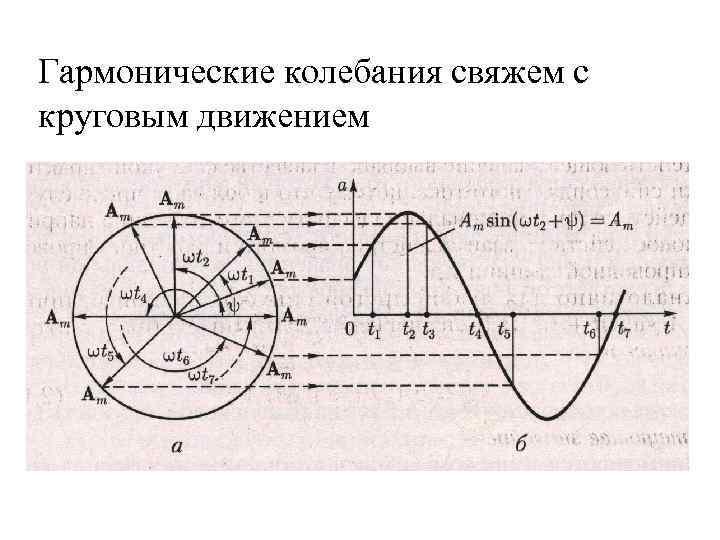Гармонические колебания свяжем с круговым движением
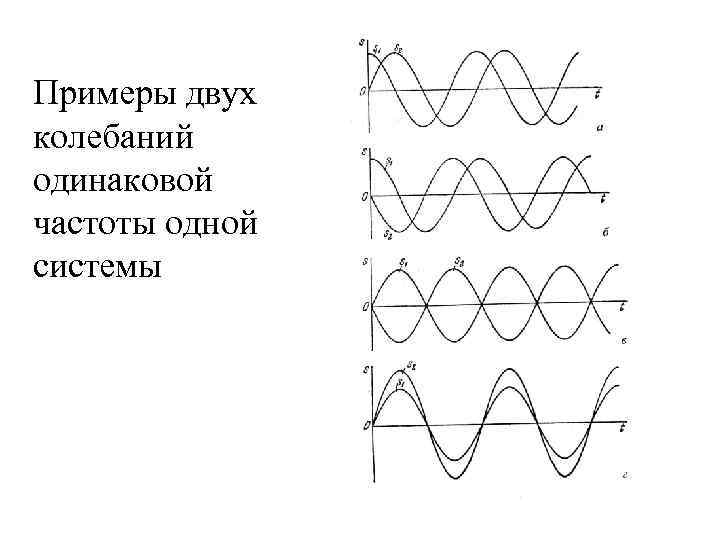Примеры двух колебаний одинаковой частоты одной системы
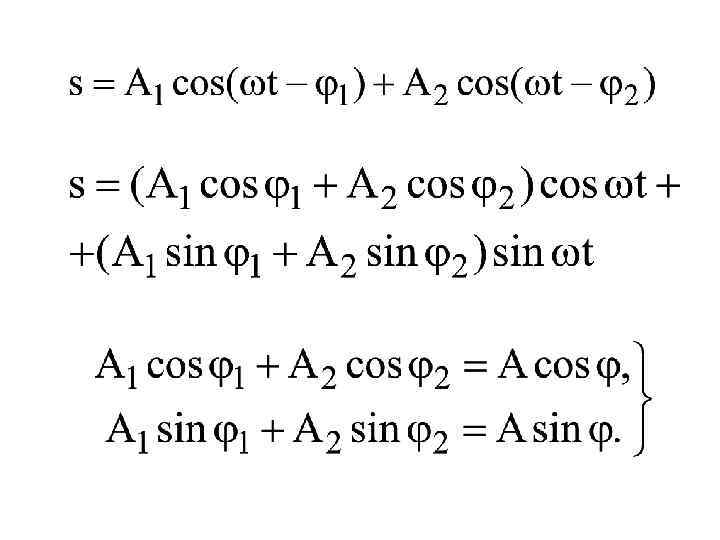
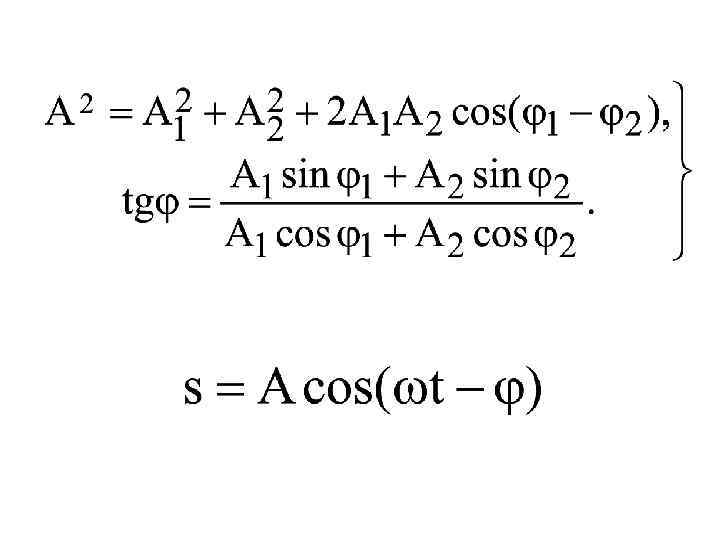
Векторная диаграмма сложения колебаний одной системы
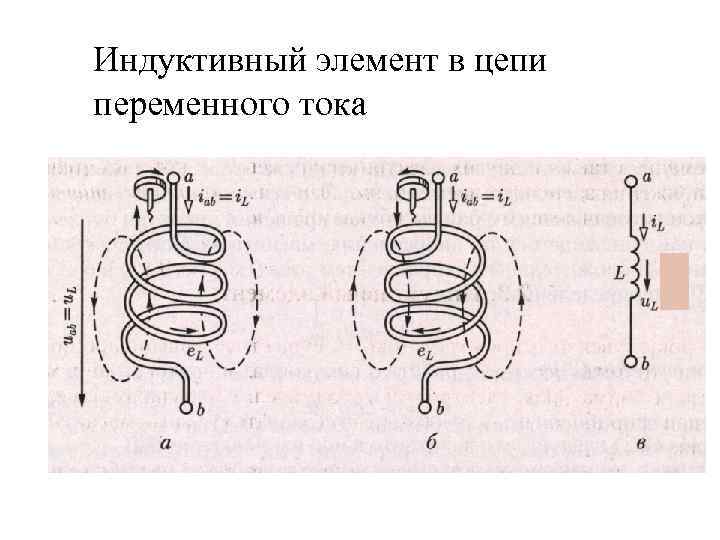Индуктивный элемент в цепи переменного тока
Вокруг тока или движущегося заряда – магнитное поле. Если iab постоянен, поток - постоянен. В индуктивности определяем потокосцепление - поток от каждого витка.
; - собственное потокосцепление. при переменном токе и препятствует изменению тока.
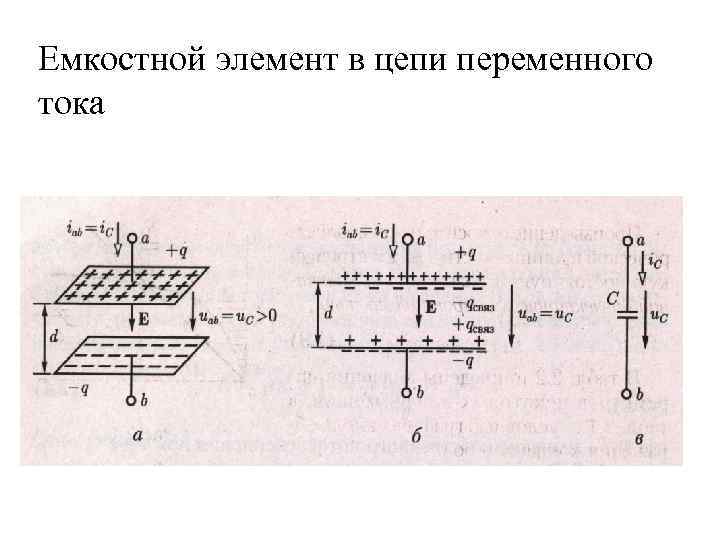Емкостной элемент в цепи переменного тока
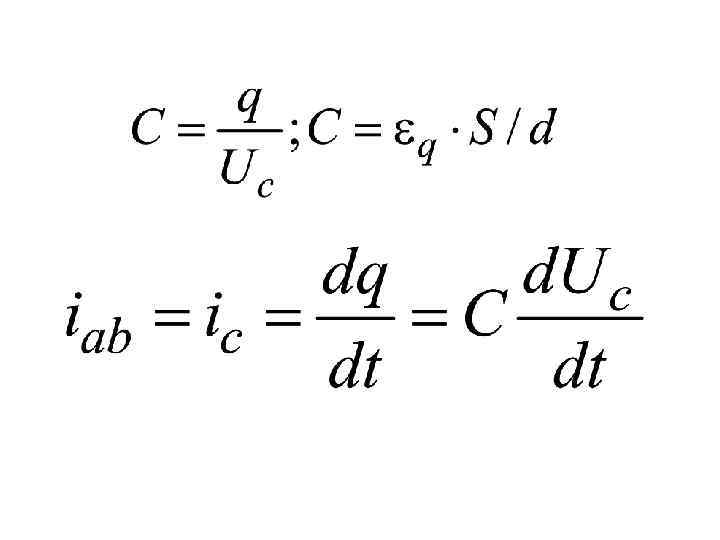
Сосредоточенные элементы цепи переменного тока
1 – резистивный элемент учитывает необратимые преобразования электрической энергии в тепловую энергию
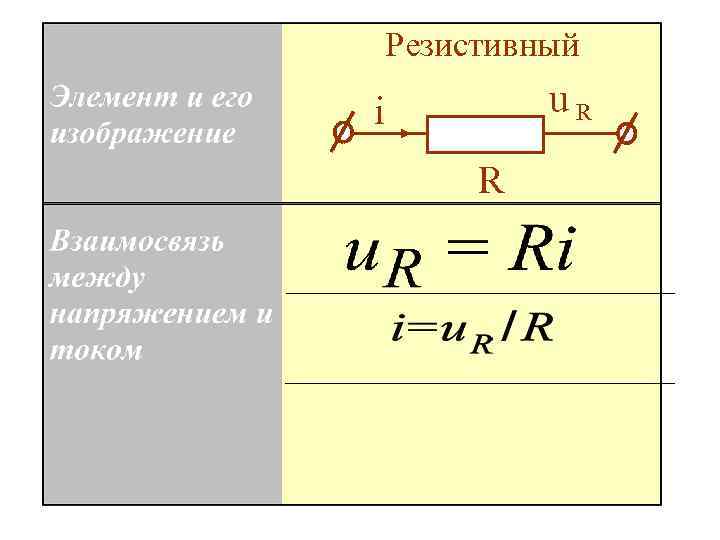Резистивный u. R i R
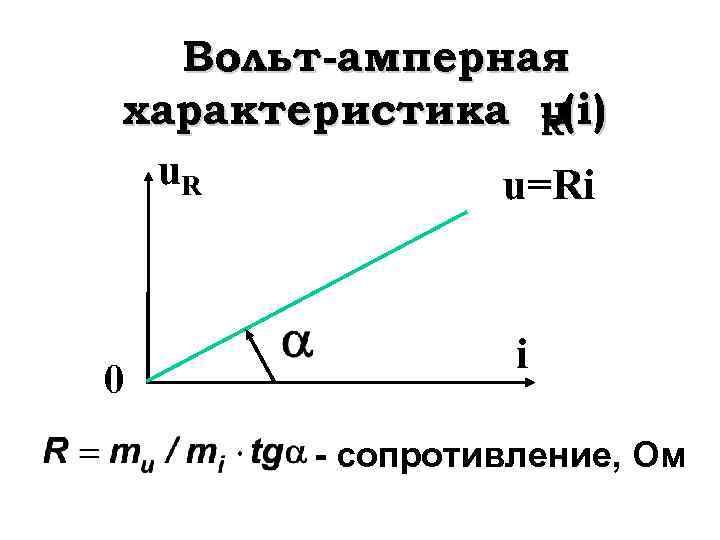Вольт-амперная характеристика u(i) R u=Ri 0 i - сопротивление, Ом
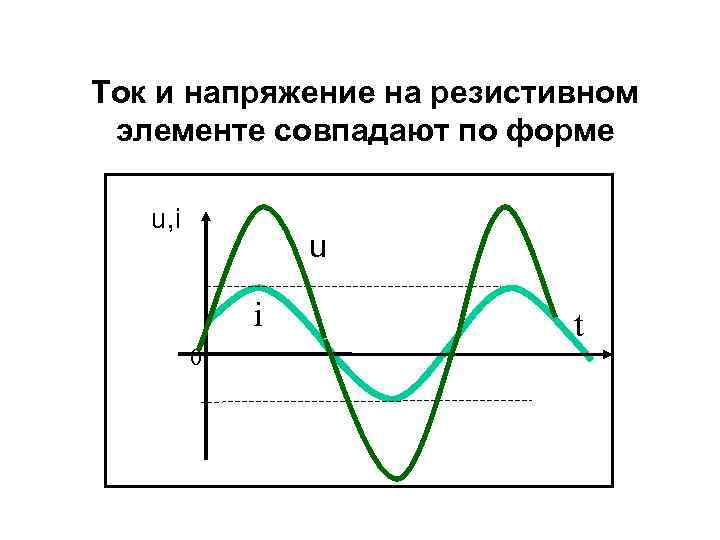Ток и напряжение на резистивном элементе совпадают по форме u, i u i 0 t
2. Индуктивный элемент учитывает накопление энергии в магнитном поле катушки индуктивности
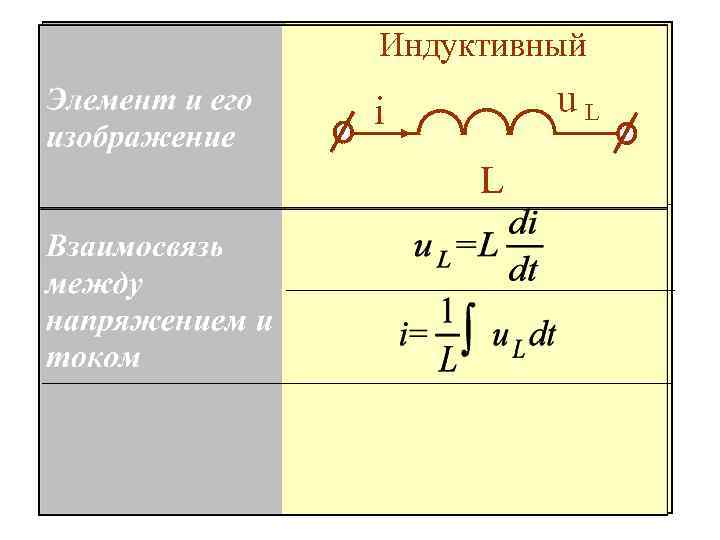Индуктивный u. L i L
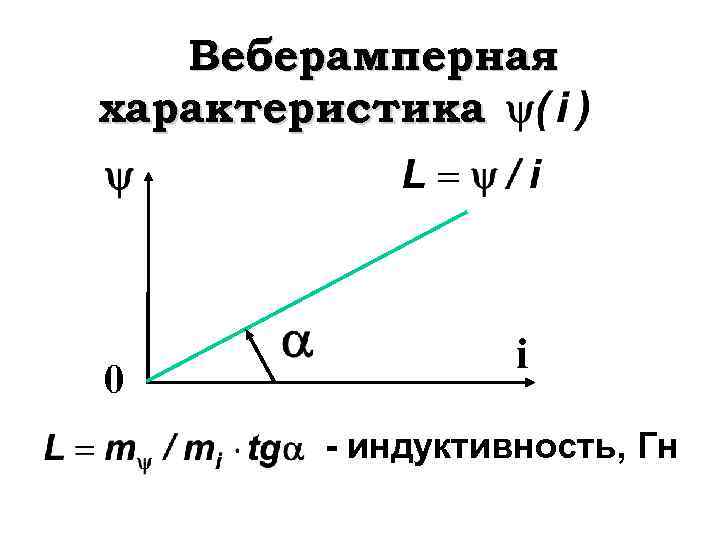Веберамперная характеристика 0 i - индуктивность, Гн
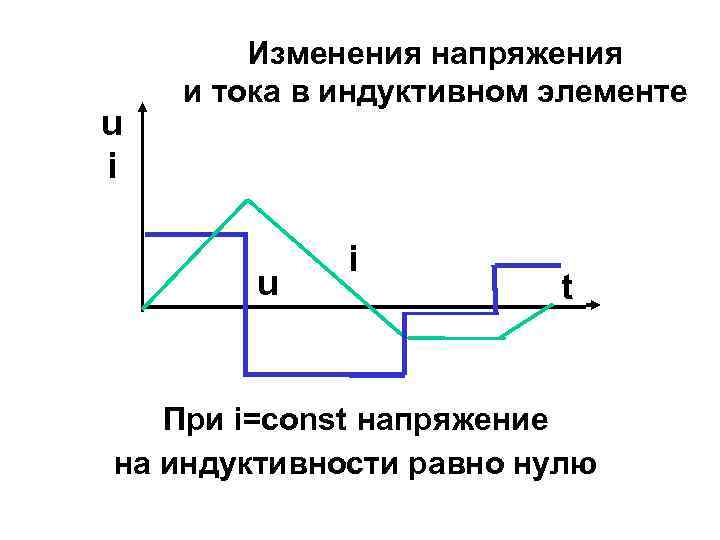u i Изменения напряжения и тока в индуктивном элементе u i t При i=const напряжение на индуктивности равно нулю
Если ток меняется по линейному закону: то напряжение на этих участках времени будет постоянным
3. Емкостный элемент учитывает накопление энергии в электрическом поле конденсатора
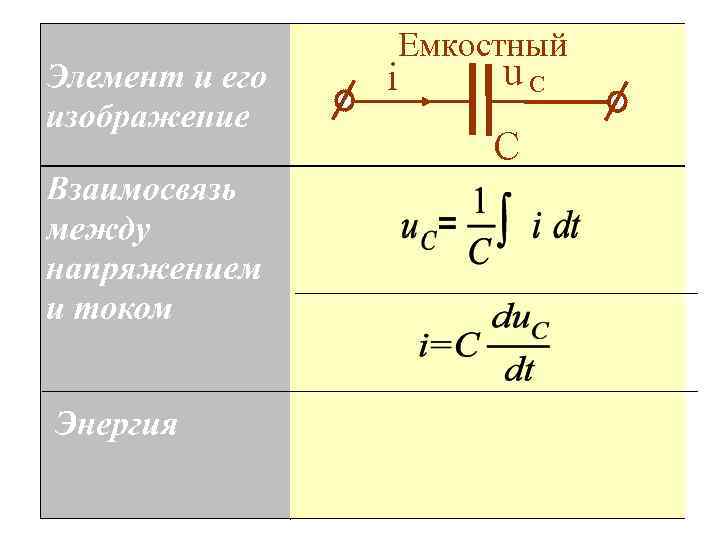Емкостный i u. С С
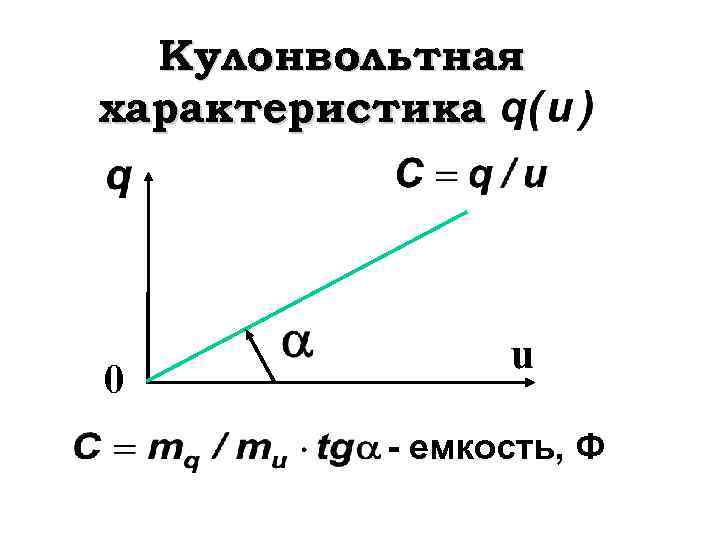Кулонвольтная характеристика 0 u - емкость, Ф
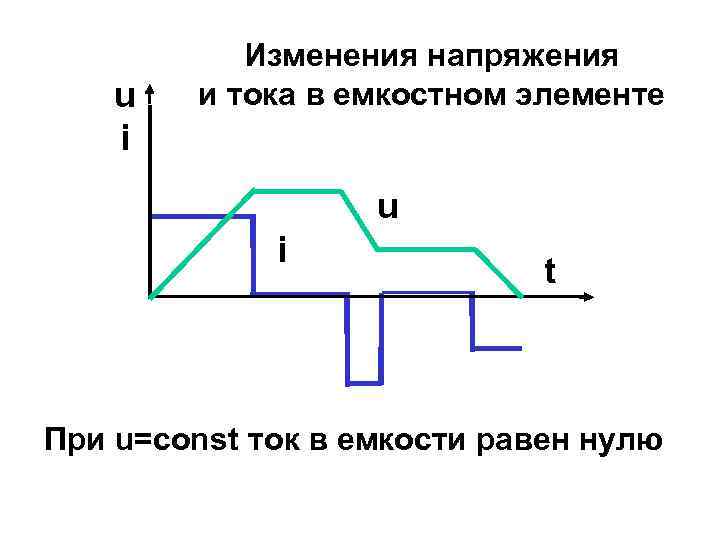u i Изменения напряжения и тока в емкостном элементе u i t При u=const ток в емкости равен нулю
Если напряжение меняется по линейному закону: то ток на этих участках времени будет постоянным
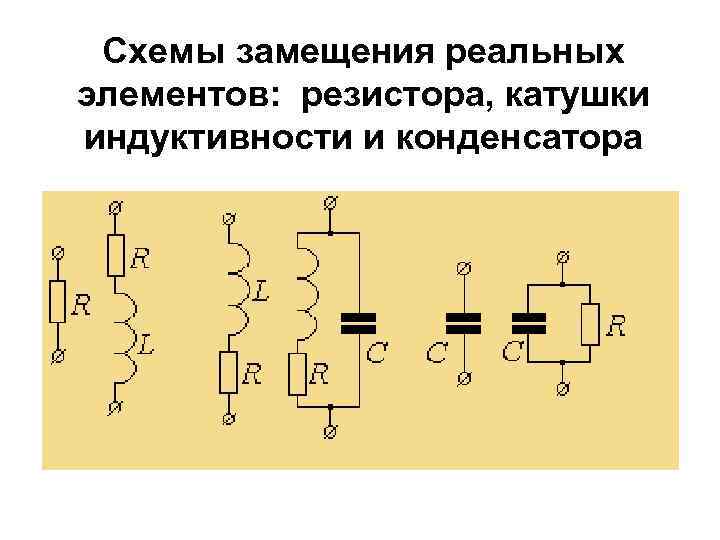Схемы замещения реальных элементов: резистора, катушки индуктивности и конденсатора
где: - мгновенное значение - амплитудное значение (рад/с) - угловая частота (1/с) или (Гц) - циклическая частота
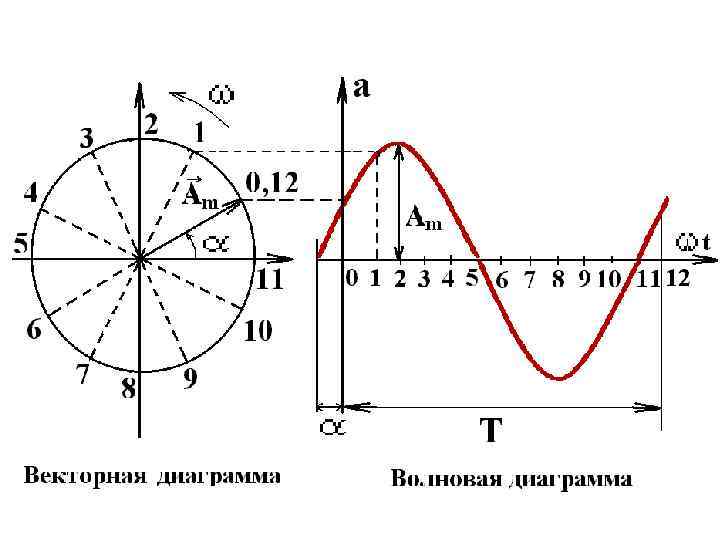
Векторная диаграмма - это изображение синусоиды в виде вектора в прямоугольной системе координат, длина которого равна амплитуде синусоиды, а угол поворота равен начальной фазе и отсчитывается от оси абсцисс против часовой стрелки. Волновая диаграмма - это развертка вращающегося вектора во времени.
Действующие значения гармонических токов и напряжений
Действующие значения тока и напряжения характеризуют тепловое действие в линейном резистивном элементе с сопротивлением R
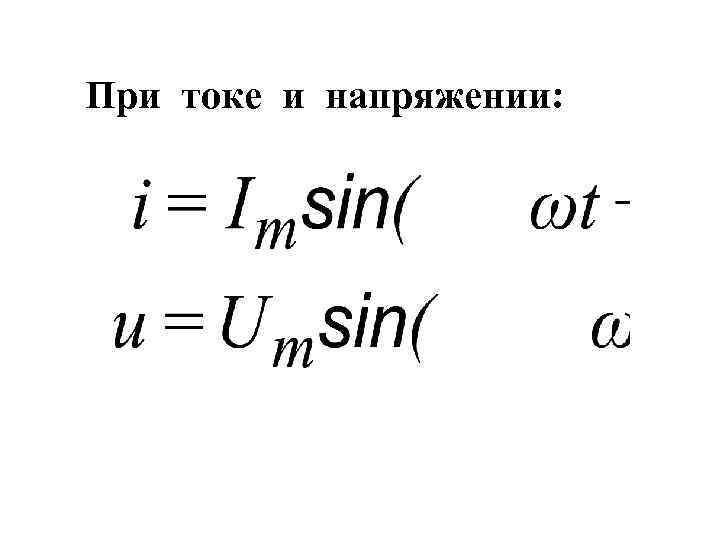При токе и напряжении:
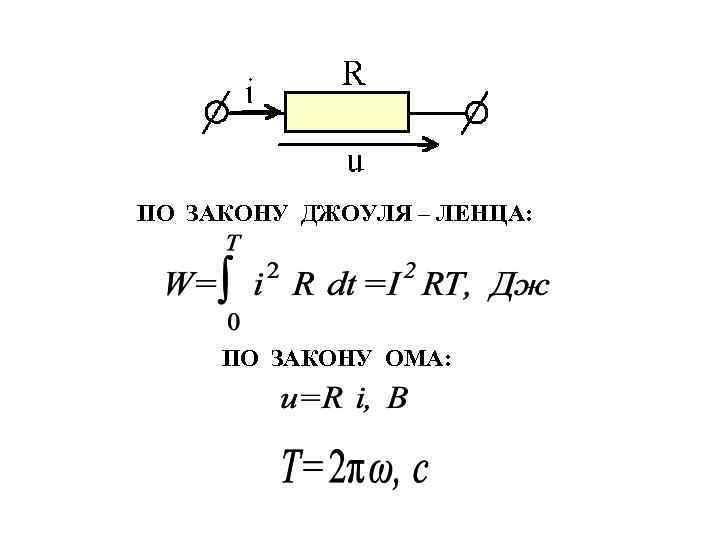R i + u ПО ЗАКОНУ ДЖОУЛЯ – ЛЕНЦА: ПО ЗАКОНУ ОМА:
Действующее значение тока
Действующее значение напряжения
Действующее значение гармонического тока i численно равно такому постоянному току I , который за время Т в том же сопротивлении R выделяет такое же количества тепла W
Действующие значения тока и напряжения не зависят от угловой частоты и начальной фазы
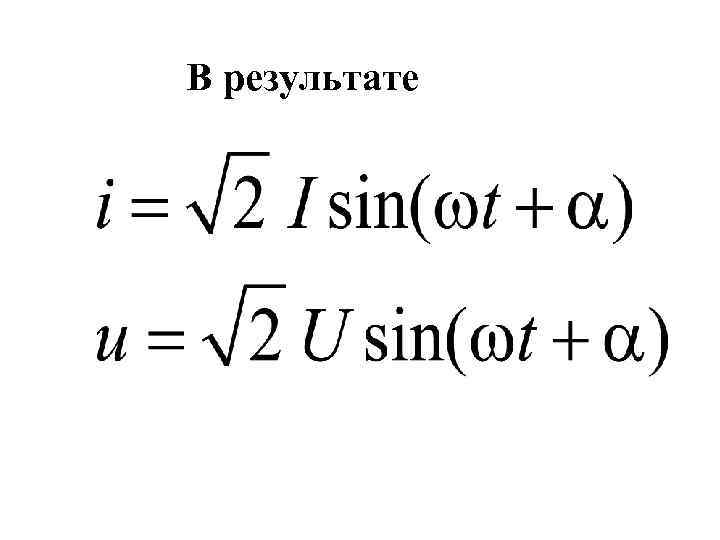В результате
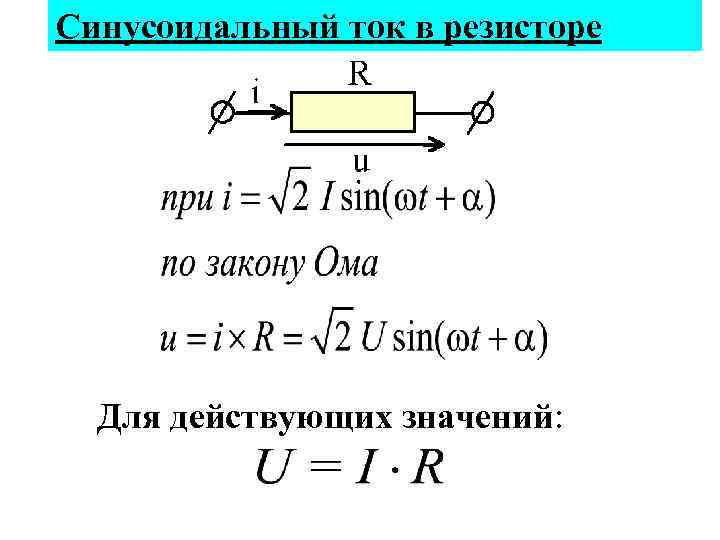Синусоидальный ток в резисторе Для действующих значений:
Ток и напряжение в резисторе совпадают по фазе. Мгновенная активная мощность равна: Средняя за период Т активная мощность:
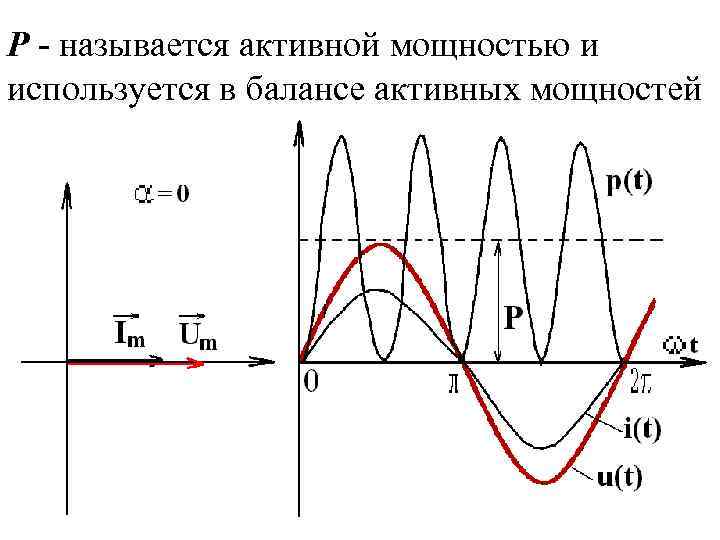Р - называется активной мощностью и используется в балансе активных мощностей
Синусоидальный ток в индуктивности
Для действующих значений: где - индуктивное реактивное сопротивление В индуктивности напряжение опережает ток на 900. Мгновенная активная мощность равна:
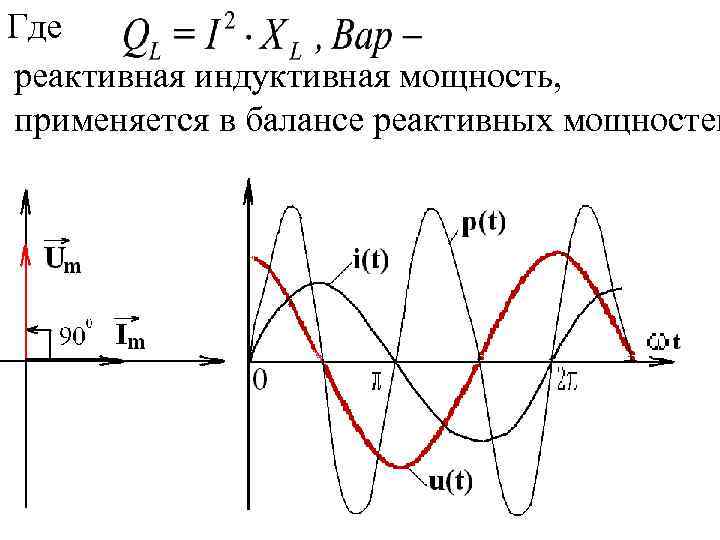Где реактивная индуктивная мощность, применяется в балансе реактивных мощностей
Когда индуктивность потребляет энергию, которая запасается в магнитном поле; запасенная энергия Когда возвращается в сеть. Средняя за период Т активная мощность Р=0.
Синусоидальный ток в ёмкости i С
Для действующих значений:
В ёмкости напряжение отстаёт от тока на 900 Мгновенная активная мощность равна:
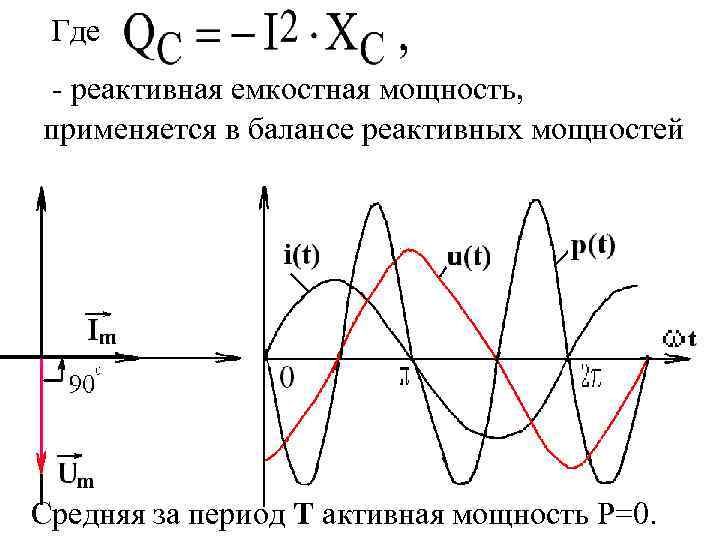Где - реактивная емкостная мощность, применяется в балансе реактивных мощностей Средняя за период Т активная мощность Р=0.
Когда ёмкость потребляет энергию, которая запасается в электрическом поле; Когда запасенная энергия возвращается в сеть. Средняя за период Т активная мощность Р=0.
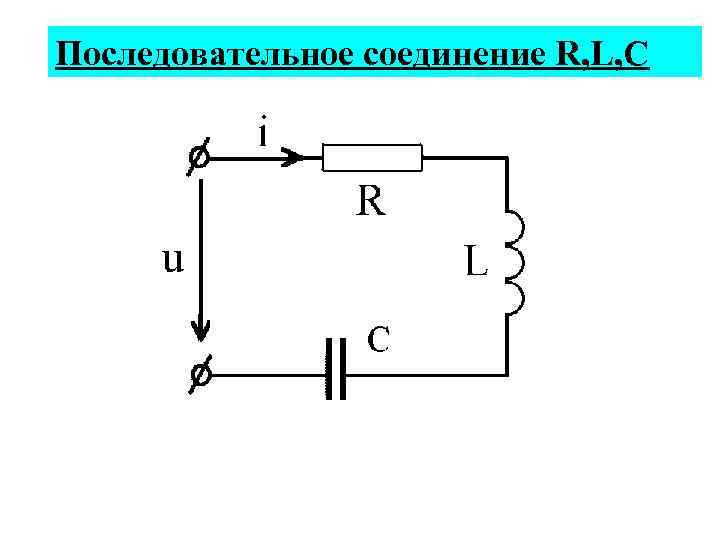Последовательное соединение R, L, C
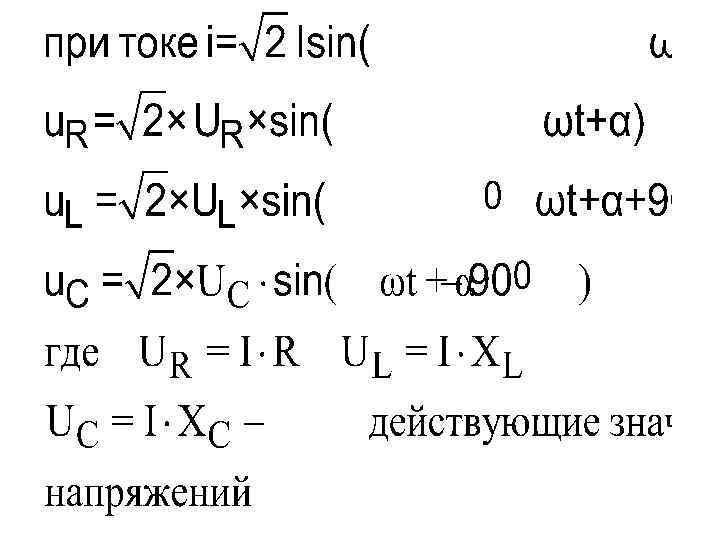
По второму закону Кирхгофа: Построим векторную диаграмму для действующих значений
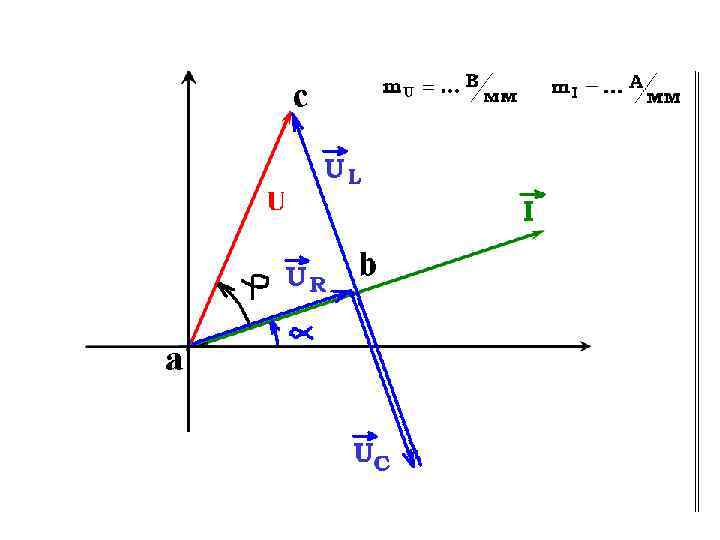
Получим: а) треугольник напряжений abc - мгновенное значение входного напряжения
б) треугольник сопротивлений Где: Z (Ом) – полное сопротивление - угол нагрузки
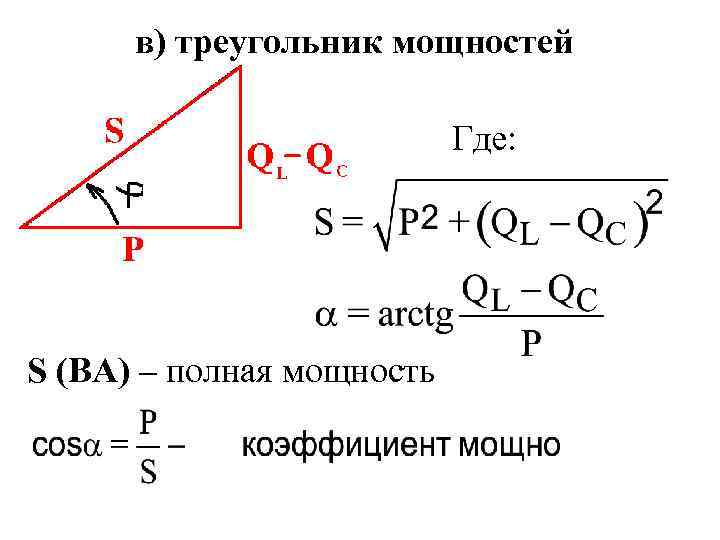в) треугольник мощностей Где: S (ВА) – полная мощность
- показывает, какая часть полной мощности используется в виде активной мощности
На основании треугольника мощностей составляется баланс мощности в эл. цепи а) мощность источников: б) потребляемая мощность
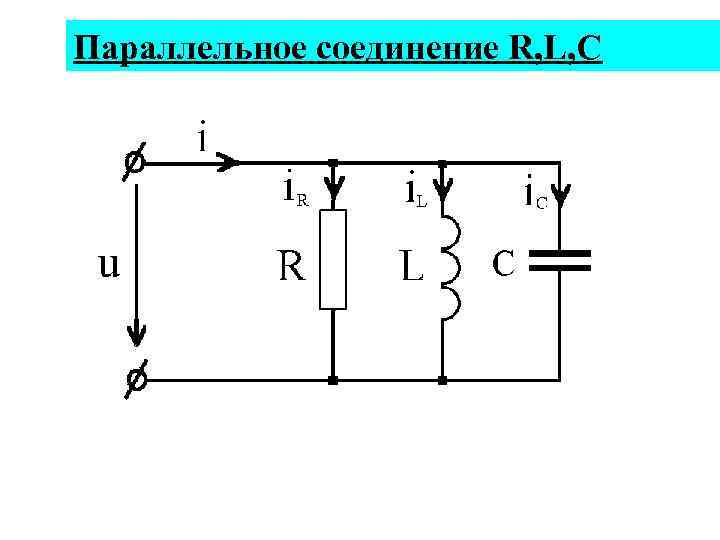Параллельное соединение R, L, C
По первому закону Кирхгофа для входного тока: Построим векторную диаграмму для действующих значений токов
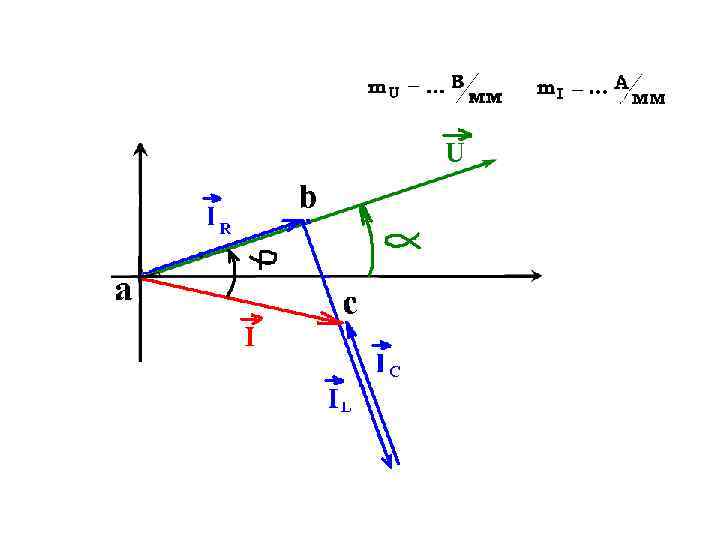
Получим: а) треугольник токов abc
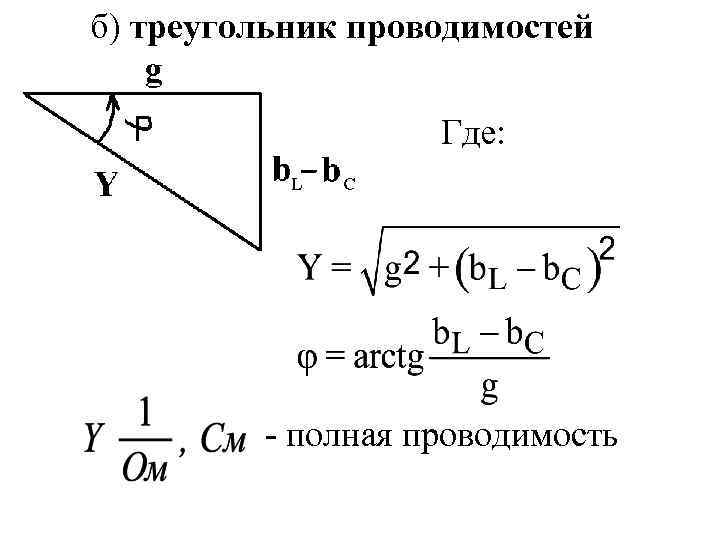б) треугольник проводимостей Где: - полная проводимость
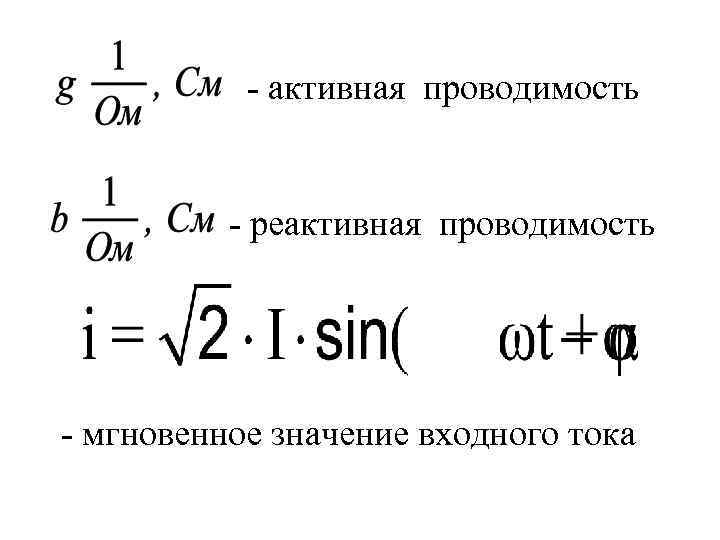- активная проводимость - реактивная проводимость - мгновенное значение входного тока