ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ оглавление 1 2 3 4

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

оглавление 1. 2. 3. 4. 5. 6. 7. 8. Постановка задачи линейного программирования Задача об использовании сырья Задача о составлении рациона Задача о максимальной загрузке оборудования Примеры задач Формы записи задач линейного программирования Геометрическая интерпретация задач

ПОСТАНОВКА ЗАДАЧ ►Опр. Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением задач оптимизации и разработкой методов их решения. В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции при условиях , где f и gi – заданные функции, а bi – некоторые действительные числа.

ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Если f и gi – линейные функции, то решается задача линейного программирования. Если же хотя бы одна функция будет нелинейной, то это задача нелинейного программирования (выпуклого, целочисленного, параметрического, динамического и т. д. ) Многие задачи линейного программирования являются математическими моделями разнообразных реальных процессов, наблюдаемых в экономике. Эти методы учитывают только линейные связи между объектами исследования. Среди многочисленных задач линейного программирования можно выделить задачи об использовании сырья, о составлении рациона, транспортную задачу и т. д.

ЗАДАЧА ОБ ИСПОЛЬЗОВАНИИ СЫРЬЯ Предприятие выпускает n видов продукции P 1, P 2, …Pn, используя при этом m-видов сырья S 1, S 2, …Sm, запасы которого равны соответственно b 1, b 2, …bm. На каждый Pi вид продукции используется Si вида сырья в количестве aij, единиц. Каждый вид продукции Pi приносит предприятию прибыль сj. Требуется составить такой план производства, чтобы прибыль от его реализации была максимальной, при имеющихся запасах сырья.

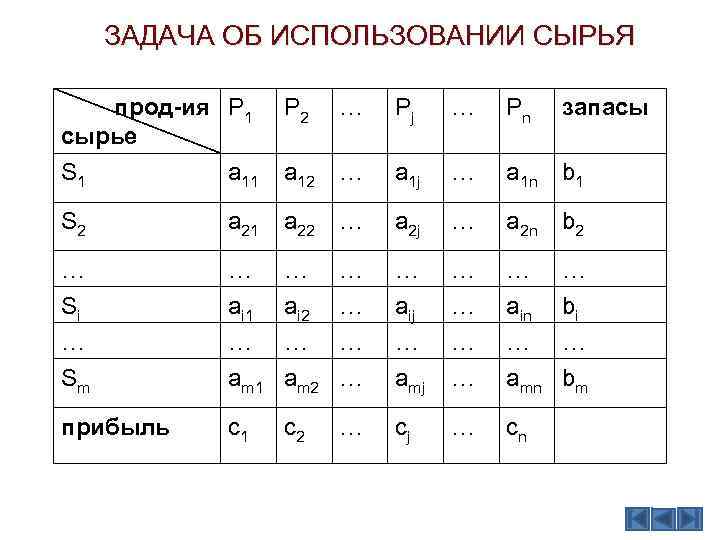ЗАДАЧА ОБ ИСПОЛЬЗОВАНИИ СЫРЬЯ прод-ия P 1 сырье S 1 a 11 P 2 … Pj … Pn запасы a 12 … a 1 j … a 1 n b 1 S 2 a 21 a 22 … a 2 j … a 2 n b 2 … Si … Sm … ai 1 … am 1 … ai 2 … am 2 … … … aij … amj … … … ain … amn … bi … bm прибыль c 1 c 2 … cj … cn

ЗАДАЧА ОБ ИСПОЛЬЗОВАНИИ СЫРЬЯ Обозначим x 1, x 2, … xn – кол-во выпускаемой продукции каждого вида. Тогда для сырья S 1 расход будет следующий: и т. д. Получаем систему ограничений: система ограничений Количество выпускаемой продукции - величина положительная, поэтому Прибыль предприятия от реализации продукции равна: Целевая функция

ЗАДАЧА ОБ ИСПОЛЬЗОВАНИИ СЫРЬЯ Итак, получаем мат. модель поставленной задачи. Среди неотрицательных решений системы (1) найти такое, которое дает максимальное значение целевой функции (2).

ЗАДАЧА О СОСТАВЛЕНИИ РАЦИОНА Имеется n видов продукции P 1, P 2, …Pn по цене за единицу продукции соответственно с1, с2, …сn. В продукции содержатся питательные вещества S 1, S 2, …Sm. Известна суточная потребность организма в питательном веществе Si, она должна быть не менее bi. Требуется составить суточный рацион n видов продукции, который будет иметь минимальную стоимость, если известно, что в Pj виде продукции содержится питательного вещества Si в количестве aij.

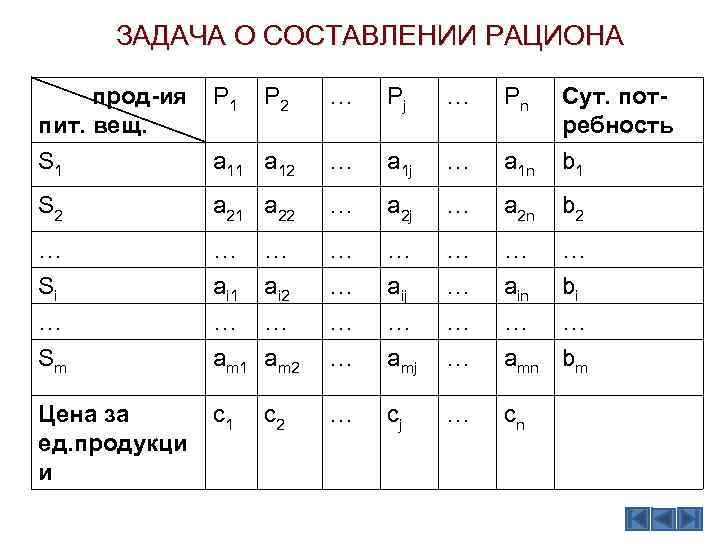ЗАДАЧА О СОСТАВЛЕНИИ РАЦИОНА прод-ия пит. вещ. S 1 P 2 … Pj … Pn a 11 a 12 … a 1 j … a 1 n Сут. потребность b 1 S 2 a 21 a 22 … a 2 j … a 2 n b 2 … Si … Sm … ai 1 … am 1 … ai 2 … am 2 … … … aij … amj … … … ain … amn … bi … bm Цена за ед. продукци и c 1 c 2 … cj … cn

ЗАДАЧА О СОСТАВЛЕНИИ РАЦИОНА Обозначим x 1, x 2, … xn – кол-во продуктов, входящих в рацион. Тогда суточная потребность в питательном веществе S 1 должна быть не менее b 1: и т. д. Получаем систему ограничений: Минимальная стоимость суточного рациона равна:

ЗАДАЧА О МАКСИМАЛЬНОЙ ЗАГРУЗКЕ ОБОРУДОВАНИЯ Пусть имеется m видов оборудования S 1, S 2, …Sm, с помощью которых обрабатываются изделия вида P 1, P 2, …Pn. Известен фонд полезного времени оборудования b 1, b 2, …bm. Требуется рассчитать план выпуска изделий, обеспечивающий максимальную загрузку оборудования, если известно, что при изготовлении одной единицы изделия вида Pj требуется времени на оборудовании Si в количестве aij единиц.

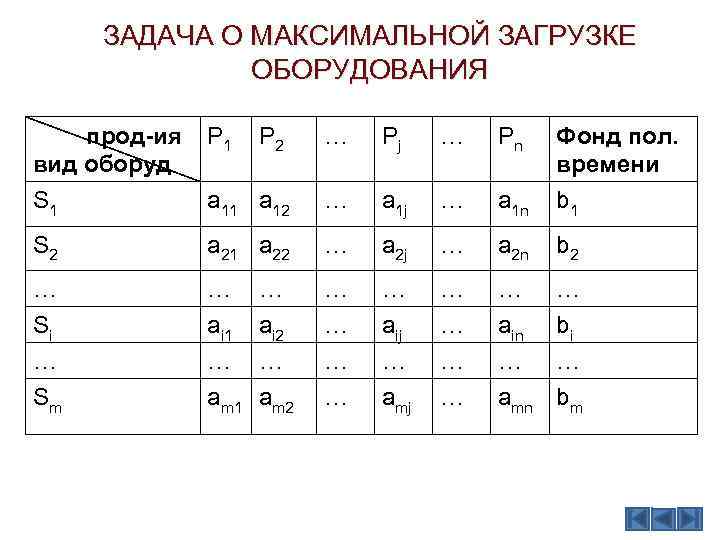ЗАДАЧА О МАКСИМАЛЬНОЙ ЗАГРУЗКЕ ОБОРУДОВАНИЯ прод-ия вид оборуд S 1 P 2 … Pj … Pn a 11 a 12 … a 1 j … a 1 n Фонд пол. времени b 1 S 2 a 21 a 22 … a 2 j … a 2 n b 2 … Si … Sm … ai 1 … am 1 … … … aij … amj … … … ain … amn … bi … bm … ai 2 … am 2

ЗАДАЧА О МАКСИМАЛЬНОЙ ЗАГРУЗКЕ ОБОРУДОВАНИЯ Обозначим x 1, x 2, … xn – кол-во единиц выпускаемой продукции каждого вида P 1, P 2, …Pn. Тогда расход времени оборудования S 1 будет следующим: и т. д. Получаем систему ограничений: Составим функцию F загрузки оборудования:

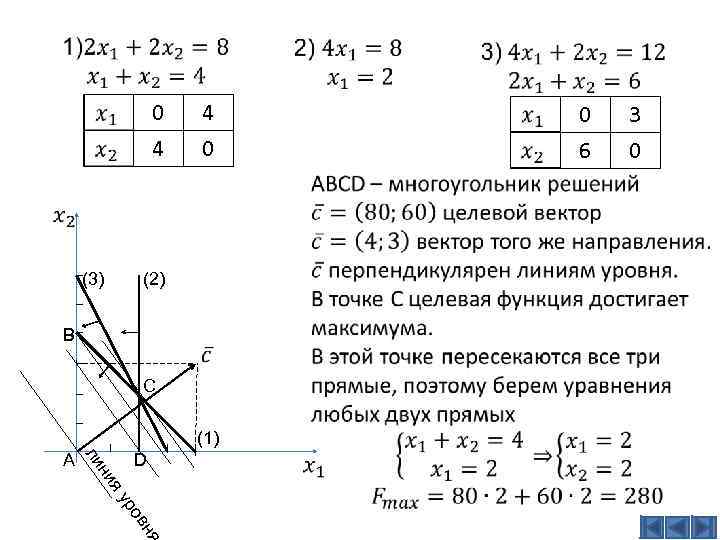
ПРИМЕРЫ ЗАДАЧ Пример 1 Мебельный кооператив делает стулья и табуретки. Используется древесина двух сортов (1 и 2) по 8 единиц каждой. На стул расходуется древесина 1 и 2 вида, соответственно 2 и 4 единицы, на табурет расходуется древесина только 1 вида в количестве 2 единиц. Для того, чтобы сделать стул, надо затратить 4 часа, а табурет 2 часа. Определить сколько следует изготовлять кооперативу стульев и табуреток, если прибыль от реализации одного табурета 60 рублей, а одного стула 80 рублей. А общее количество затрат труда не более 12 часов.

прод-ия стул табурет запасы сырье Древесина 1 2 2 8 Древесина 2 4 _ 8 Трудоемкость 4 2 12 прибыль 80 60

ПОСТАНОВКА ЗАДАЧ Пример 2 На трех станках обрабатывается 2 вида изделий B 1 и B 2. Трудоемкость обработки единицы изделия В 1 на каждом станке 4, 0 и 2 единицы времени, соответственно. А изделие В 2 – 2, 3 и 2 единицы времени. Фонд полезного времени работы первого станка - 48 часов, второго – 36 часов, а третьего 40. Цена единицы изделия В 1 – 15 рублей, изделия В 2 – 12 рублей. Найти план производства изделий, обеспечивающий выполнение плана не менее чем на 120 рублей при наименьшей загрузке оборудования.

ПОСТАНОВКА ЗАДАЧ Пример 3 Кооператив шьет женские и мужские костюмы, на которые идет 3 вида ткани. Расход ткани каждого вида на женский костюм 2, 4 и 1 метр, соответственно. На мужской костюм – 3, 3 и 0. Количество ткани каждого вида составляет 21, 27 и 5 метров. Сколько костюмов надо сшить кооперативу, чтобы прибыль была наибольшей, если оба костюма дают прибыль по 400 рублей.

ПОСТАНОВКА ЗАДАЧ Пример 4 Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства (мощность) первой линии 60 изделий, второй линии 80 изделий. На радиоприемник первой модели расходуется 15 однотипных элементов электронных схем, на радиоприемник второй модели 10 таких же элементов. Максимальный суточный запас используемых элементов равен 950 единиц. Прибыли от реализации одного радиоприемника первой и второй моделей равны 40$ и 20$ соответственно. Определите оптимальные суточные объемы производства первой и второй моделей.

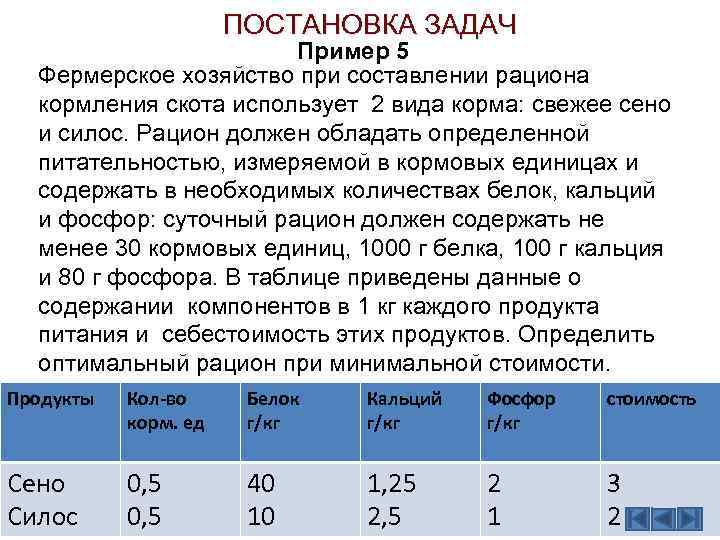ПОСТАНОВКА ЗАДАЧ Пример 5 Фермерское хозяйство при составлении рациона кормления скота использует 2 вида корма: свежее сено и силос. Рацион должен обладать определенной питательностью, измеряемой в кормовых единицах и содержать в необходимых количествах белок, кальций и фосфор: суточный рацион должен содержать не менее 30 кормовых единиц, 1000 г белка, 100 г кальция и 80 г фосфора. В таблице приведены данные о содержании компонентов в 1 кг каждого продукта питания и себестоимость этих продуктов. Определить оптимальный рацион при минимальной стоимости. Продукты Кол-во корм. ед Белок г/кг Кальций г/кг Фосфор г/кг стоимость Сено Силос 0, 5 40 10 1, 25 2, 5 2 1 3 2

ФОРМЫ ЗАПИСИ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Опр. Общей задачей ЛП называется задача, которая состоит в определении max (min) значения функции: при ограничениях: где aij, bi, cj – заданные постоянные величины

ФОРМЫ ЗАПИСИ ЗАДАЧ ЛП Опр. Стандартной (симметричной) задачей ЛП называется задача, которая состоит в определении max значения целевой функции (1), при выполнении условий (2), (5), где k=l, p=n; или в определении min значения целевой функции (1), при выполнении условий (4), (5), где m=0, p=n. Опр. Основной (канонической) задачей ЛП называется задача, которая состоит в определении max значения целевой функции (1), при выполнении условий (3), (5), где k=0, m=l, p=n.

ФОРМЫ ЗАПИСИ ЗАДАЧ ЛП Указанные выше три формы записи задач ЛП (общая, симметричная и каноническая) эквивалентны в том смысле, что каждая задача может быть с помощью несложных преобразований переведена из одной формы в другую. Чтобы перейти от одной задачи ЛП к другой нужно уметь: 1. переходить от минимизации целевой функции к максимизации; 2. переходить в системе ограничений от неравенств к уравнениям и наоборот.

ФОРМЫ ЗАПИСИ ЗАДАЧ ЛП Примеры

ФОРМЫ ЗАПИСИ ЗАДАЧ ЛП Пример 1. Записать задачу ЛП в канонической форме:

ФОРМЫ ЗАПИСИ ЗАДАЧ ЛП Пример 2. Записать задачу ЛП в симметричной форме:

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Графически можно решать задачи ЛП в следующих случаях: 1. если 2. n = 3 (сложно рисовать плоскости на листе, т. к. лист – 2 -хмерное пространство) 3. , для задач, заданных в канонической форме. Геометрический метод не является общим методом решения задач ЛП. Он выполняет лишь вспомогательную роль и позволяет наглядно представить себе свойства задачи ЛП и ее решение симплекс-методом.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Рассмотрим задачу:

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Пару неизвестных х1 и х2 рассмотрим как координаты точек плоскости в декартовой системе координат с осями х1 и х2. Опр. Множество пар значений Х(х1, х2), удовлетворяющих системе ограничений (2) – это множество допустимых решений задачи ЛП. Тогда множеству допустимых решений задачи в плоскости Х 1 ОХ 2 будет отвечать некоторая область. Определим вид этой области.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Каждое из неравенств системы (2) заменим на уравнение: Это будет граничная прямая, делящая плоскость на две части (на две полуплоскости). Чтобы выяснить, какая полуплоскость удовлетворяет неравенству, берем любую точку М(x’, y’) из любой полуплоскости (не на граничной прямой) и подставляем в неравенство. Если неравенство верно, то полуплоскость, которой принадлежит точка М, является искомой. Если неравенство оказалось неверным, то следует выбрать противоположную полуплоскость.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Очевидно, что решением системы (2) будут точки, принадлежащие всем неравенствам одновременно. Совокупность этих точек называется многоугольником решений. Для случая n > 2 совокупность этих точек называется многогранником решений. Опр. Множество М называется выпуклым, если с любыми двумя точками a и b, принадлежащими М оно содержит и отрезок [a; b], их соединяющий.

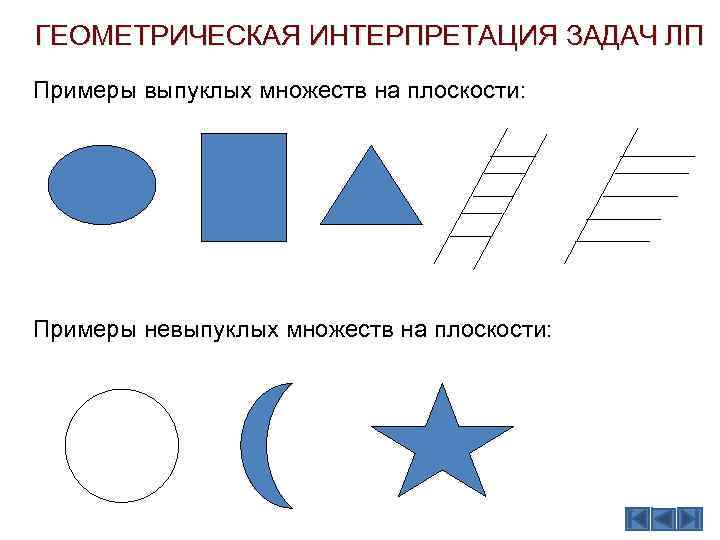ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Примеры выпуклых множеств на плоскости: Примеры невыпуклых множеств на плоскости:

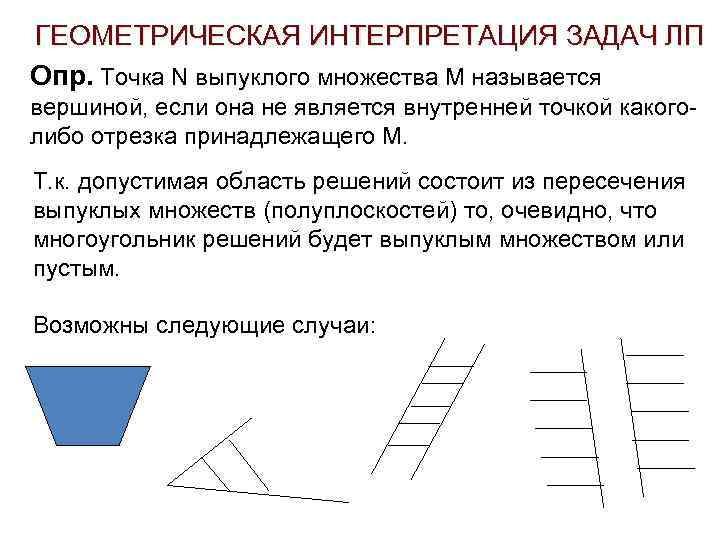ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Опр. Точка N выпуклого множества М называется вершиной, если она не является внутренней точкой какоголибо отрезка принадлежащего М. Т. к. допустимая область решений состоит из пересечения выпуклых множеств (полуплоскостей) то, очевидно, что многоугольник решений будет выпуклым множеством или пустым. Возможны следующие случаи:

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Опр. Рассмотрим поведение целевой функции При фиксированном значении F = h целевая функция определяет на плоскости прямую линию при изменении F получим семейство параллельных прямых, называемых, линиями уровня.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Вектор называется целевым вектором или вектором направлений. Вектор перпендикулярен к каждой линии уровня. Вектор показывает направление наибольшего возрастания (убывания) целевой функции. Теорема. Если основная задача ЛП имеет решение, то max (min) значение целевая функция задачи принимает в одной из вершин многоугольника (многогранника) решений. Если max (min) значение целевая функция задачи принимает более чем в одной вершине, то она принимает его на прямой (или на отрезке).

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Если построить на одном рисунке область допустимых решений, вектор и одну из линий уровня F = 0, то задача сводится к определению в области допустимых решений точки в направлении вектора , через которую проходит линия уровня Fmax (Fmin), соответствующая наибольшему (наименьшему) значению функции F. Это и есть графический способ решения задачи ЛП. Возможны следующие случаи: 1. задача имеет единственное решение; 2. задача имеет бесконечное множество решений; 3. целевая функция не ограничена – задача не имеет решения; 4. область допустимых решений пуста – задача не имеет решения.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП max min h 3 h 1 h 2

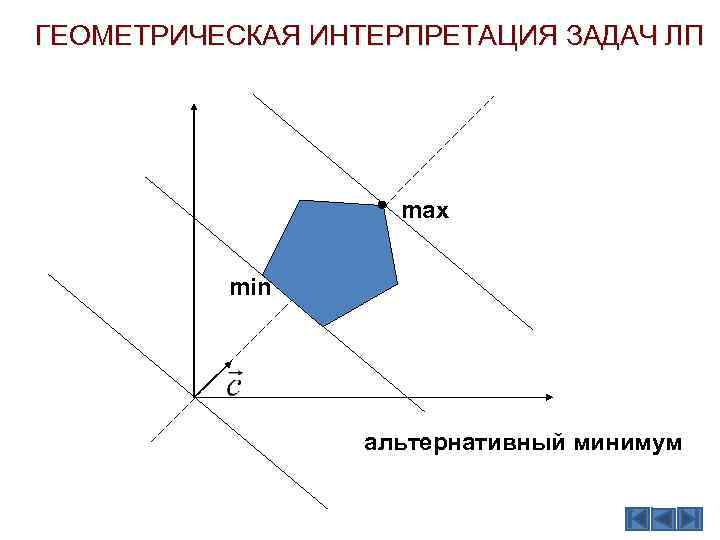ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП max min альтернативный минимум

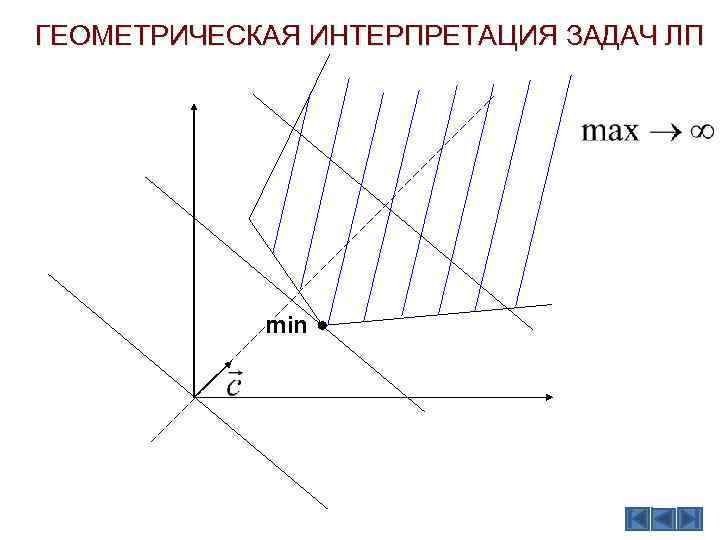ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП min

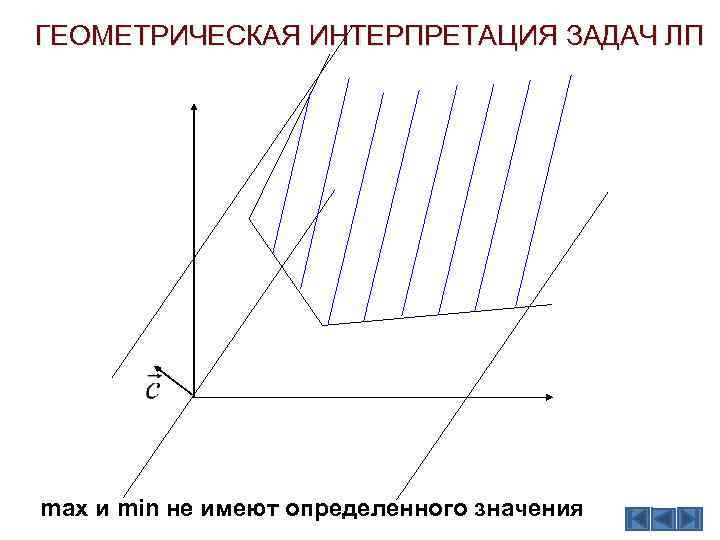ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП max и min не имеют определенного значения

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧ ЛП Нахождение решения задачи ЛП включает в себя следующие этапы: 1. Рисуем граничные прямые для полуплоскостей системы (2); 2. Находим многоугольник решений; 3. Строим целевой вектор; 4. Строим линии уровня; 5. Находим точку дающую min или max; 6. Находим Fmin или Fmax

0 4 4 0 0 6 (3) (2) B C (1) D я вн ро я у ни ли A 3 0

Примеры