Линейное программирование Многие задачи можно сформулировать

Линейное программирование

Многие задачи можно сформулировать как задачи максимизации или мини мизации некой цели в условиях ограниченности ресурсов и наличия конкурирую щих ограничений. Если удастся задать цель в виде линейной функции нескольких переменных и сформулировать ограничения в виде равенств или неравенств, свя зывающих эти переменные, мы получим задачу линейного программирования. Задачи линейного программирования часто встре чаются в разнообразных практических приложениях. Рассмотрим при мер ыработки предвыборной политики. в Политическая задача Цель политика – выиграть выборы. В его избирательном округе есть районы трех типов – городские, пригородные и сельские. В этих районах зарегистрировано, соответственно, 100000, 200000 и 50000 избирателей. Чтобы добиться успеха, желательно получить большин ство голосов в каждом из трех регионов. И звестно, что определенные пункты программы могут помочь завоевать голоса определенных групп избирателей. Основными пунктами программы являются строительство до рог, контроль за использованием огнестрельного оружия, сельскохозяйственные субсидии и налог на бензин, направляемый на улучшение работы обществен ного транспорта. Согласно исследованиям его предвыборного штаба, можно оценить, сколько голосов будет приобретено или потеряно в каждой группе изби рателей, если потратить 1000 долл. на пропаганду по каждому пункту програм мы. Эта информация представлена в табл. 1. Каждый элемент данной таблицы показывает, сколько тысяч избирателей удастся привлечь, потратив 1000 долл. на агитацию в поддержку опре деленного пункта предвыборной программы. Отрицательные элементы отражают потерю голосов. Задача состоит в минимизации суммы, которая позволит заво евать 50000 голосов горожан, 100000 голосов избирателей из пригородных зон и 25 000 голосов сельских жителей.

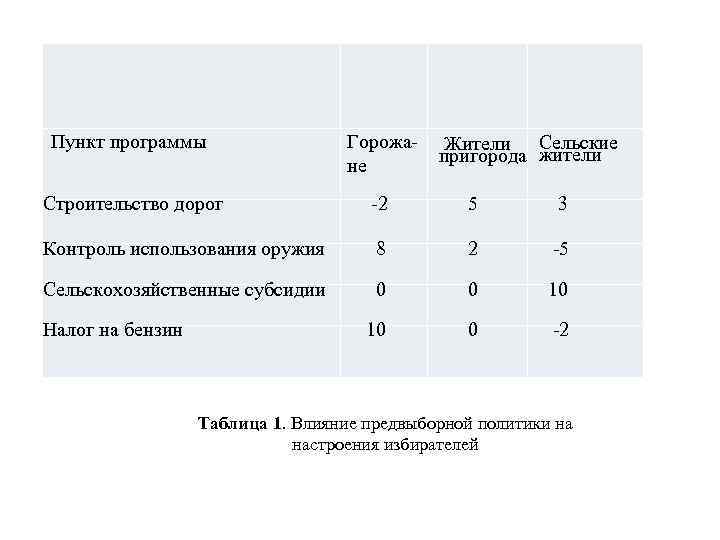Пункт программы Строительство дорог Горожа Жители Сельские пригорода жители не 2 5 3 Контроль использования оружия 8 2 5 Сельскохозяйственные субсидии 0 10 Налог на бензин 0 2 10 Таблица 1. Влияние предвыборной политики на настроения избирателей

Методом проб и ошибок можно выработать стратегию, которая позволит полу чить необходимое количество голосов, но затраты на такую стратегию могут ока заться не самыми низкими. Например, можно выделить 20 000 долл. на пропаганду строительства дорог, 0 долл. на агитацию в пользу контроля за использованием оружия, 4 000 долл. на пропаганду сельскохозяйственных субсидий и 9 000 долл. на агитацию за введение налога на бензин. При этом удастся привлечь 20 • ( 2) + 0 • (8) + 4 • (0) + 9 • 10 = 50 тысяч голосов горожан, 20 • (5) + 0 • (2) + 4 • (0) + 9 • 0 = 100 тысяч голосов жителей пригородов и 20 • (3) + 0 • ( 5) + 4 • 10 + 9 • ( 2) = 82 тысячи голосов сельских жителей. Таким образом, будет получено ровно необходимое количество голосов в городских и пригородных районах и большее количество голосов в сельской местности. (Получается, что в сельской местности привлечено голосов больше, чем наличное число избирателей!) Чтобы получить эти голоса, придется потратить на пропаганду 20+0+4+9 = 33 тысячи долларов. Возникает естественный вопрос: является ли данная стратегия наилучшей из возможных, т. е. можно ли достичь поставленных целей, потратив на пропаганду меньше денег? Ответ на этот вопрос можно получить, действуя методом проб и ошибок, однако вместо этого хотелось бы иметь некий систематический метод для ответа на подобные вопросы.

Сформулируем данный вопрос математически. Введем 4 переменные: Х 1– сумма (в тысячах долларов), потраченная на пропаганду программы строительства дорог, Х 2 – сумма (в тысячах долларов), потраченная на агитацию в пользу кон троля за использованием оружия, Х 3 – сумма (в тысячах долларов), потраченная на пропаганду программы сельскохозяйственных субсидий, Х 4 – сумма (в тысячах долларов), потраченная на агитацию за введение налога на бензин. Требование получить не менее 50 ООО голосов избирателей горожан можно записать в виде неравенства 2 x 1 + 8 x 2 + 0 x 3 + 10 x 4 ≥ 50. (1) Аналогично, требования получить не менее 100000 голосов избирателей, жи вущих в пригороде, и 25 000 голосов избирателей в сельской местности можно записать как неравенства 5 x 1 + 2 x 2 + 0 x 3 + 0 x 4 ≥ 100 (2) 3 x 1 5 x 2 + 10 x 3 2 x 4 ≥ 25 (3) Любые значения переменных x 1, x 2, x 3, x 4, удовлетворяющие неравенствам (1)–(3), позволят получить достаточное количество голосов избирателей в каждом регионе. Чтобы сделать затраты минимально возможными, необходимо минимизировать сумму, затраченную на пропаганду, т. е. минимизировать выра жение x 1 + x 2 + x 3 + x 4 (4) Хотя отрицательная агитация часто встречается в политической борьбе, отрица тельных затрат на пропаганду не бывает. Поэтому следует записать условия x 1≥ 0, x 2≥ 0, x 3≥ 0, x 4≥ 0 (5)

Поставив задачу минимизации выражения (4) при соблюдении неравенств (1)–(3) и (5), мы получаем так называемую "задачу линейного програм мирования". Запишем ее следующим образом : Минимизировать x 1 + x 2 + x 3 + x 4 (6) при условиях: 2 x 1 + 8 x 2 + 0 x 3 + 10 x 4 ≥ 50 (7) 5 x 1 + 2 x 2 + 0 x 3 + 0 x 4 ≥ 100 (8) 3 x 1 5 x 2 + 10 x 3 2 x 4 ≥ 25 (9) x 1, x 2, x 3, x 4≥ 0. (10) Решение данной задачи линейного программирования позволит политику полу чить оптимальную стратегию предвыборной агитации.

Краткий обзор задач линейного программирования Чтобы описывать свойства задач линейного программирования и алгоритмы их решения, удобно договориться, в каких формах их записывать. Мы будем использовать две формы: стандартную и каноническую (slack). Их строгое определение будет дано ниже. Неформально, стандартная форма задачи линейного программирования – это задача максимизации линей ной функции при соблюдении линейных неравенств, а каноническая форма –это задача максимизации линейной функции при соблюдении линейных равенств. Обьтчно мы будем использовать стандартную форму задач линейного програм мирования, однако при описании принципа работы симплекс алгоритма удобней использовать каноническую форму Рассмотрим задачу максимизации линейной функции n переменных при условии выполнения m линейных неравенств. Рассмотрим задачу линейного программирования с двумя переменными: Максимизировать x 1 + x 2 (11) при условиях 4 x 1 x 2 ≤ 8 (12) 2 x 1 + x 2 ≤ 10 (13) 5 x 1 2 x 2≥ 2 (14) x 1, x 2≥ 0 (15)

Любой набор значений переменных x 1 и x 2, удовлетворяющий всем ограничени ям (12)–(15), называется допустимым решением данной задачи линейного программирования. Если изобразить эти ограничения в декарто вой системе координат (x 1, x 2), как показано на рис. 1 a, то множество допусти мых решений (заштрихованная область на рисунке) образует выпуклую область в двумерном пространстве. Эта выпуклая область называется допустимой обла стью. Функция, которую мы хотим максимизировать, называется целевой функцией. Теоретически, можно было бы оценить значение целевой функции x 1 + x 2 в каждой точке допустимой области (значение целевой функции в определенной точке называется целевым значением). Затем можно найти точку, в которой целевое значение максимально; она и будет оптимальным решением. В данном примере (как и в большинстве задач линейного программирования) допустимая область содержит бесконечное множество точек, поэтому хотелось бы найти способ, который позволит находить точку с максимальным целевым значением, не прибегая к вычислению значений целевой функции в каждой точке допустимой области.

Рис. 1. а) Задача линейного программирования (12)–(15); б) Пунктирные линии показывают точки, в которых целевое зна чение равно 0, 4 и 8, соответственно

В двумерном случае оптимальное решение можно найти с помощью графи ческой процедуры. Множество точек, для которых 1 + x 2= z , при любом z x представляет собой прямую с коэффициентом наклона 1. Если мы построим график функции x 1 + x 2= 0, получится прямая с коэффициентом наклона 1, проходящая через начало координат, как показано на рис. 1 б. Пересечение данной прямой и допустимой области – это множество допустимых решений, целевое значение в которых равно 0. В данном случае пересечением прямой и допустимой области является точка (0, 0). В общем случае для любого z пе ресечением прямой x 1 + x 2= z с допустимой областью является множество допустимых решений, в которых целевое значение равно z. На рис. 1 б показа ны прямыеx 1 + x 2= 0, x 1 + x 2= 4 и x 1 + x 2= 8. Поскольку допустимая область на рис. 1 ограничена, должно существовать некое максимальное значение z, для которого пересечение прямой x 1 + x 2= z и допустимой области является непустым множеством. Любая точка этого пересечения является оптимальным решением задачи линейного программирования; в данном случае такой точкой является x 1 = 2, x 2 = 6 с целевым значением 8. То, что оптимальное решение задачи линейного программирования оказалось в некоторой вершине допустимой области, не случайно.

Максимальное значение z, при котором прямая x 1 + x 2= z пересекает допустимую область, должно находиться на границе допустимой области, поэтому пересечение данной прямой и границы допустимой области мо жет быть либо вершиной, либо отрезком. Если пересечение является вершиной, то существует единственное оптимальное решение, находящееся в данной вер шине. Если же пересечение является отрезком, то все точки этого отрезка имеют одинаковое целевое значение и являются оптимальными решениями; в частности, оптимальными решениями являются оба конца отрезка. Каждый конец отрезка –это вершина, поэтому в данном случае также существует оптимальное решение в вершине допустимой области. Несмотря на то, что для задач линейного программирования, где число пере менных больше двух, простое графическое решение построить невозможно, наши интуитивные соображения остаются в силе. В случае трех переменных каждое ограничение описывается полупространством в трехмерном пространстве. Пере сечение этих полупространств образует допустимую область. Множество точек, в которых целевая функция имеет значение z, представляет собой некую плос кость.

Если все коэффициенты целевой функции неотрицательны и начало коорди нат является допустимым решением рассматриваемой задачи линейного програм мирования, то при движении этой плоскости по направлению от начала координат получаются точки с возрастающими значениями целевой функции. (Если начало координат не является допустимым решением или некоторые коэффициенты це левой функции отрицательны, интуитивная картина будет немного сложнее. ) Как и в двумерном случае, поскольку допустимая область выпукла, множество точек, в которых достигается оптимальное целевое значение, должно содержать верши ну допустимой области. Аналогично, в случае n переменных каждое ограничение определяет полупространство в n мерном пространстве. Допустимая область, образуемая пересечением этих полупространств, называется симплексом (simplex). Целевая функция в данном случае представляет собой гиперплоскость, и благодаря выпуклости допустимой области оптимальное решение находится в некой вершине симплекса.

Симплекс алгоритм получает на входе задачу линейного программирования и возвращает оптимальное решение. Он начинает работу в некоторой вершине симплекса и выполняет последовательность итераций. В каждой итерации осу ществляется переход вдоль ребра симплекса из текущей вершины в соседнюю, целевое значение в которой не меньше (как правило, больше), чем в текущей вер шине. Симплекс алгоритм завершается при достижении локального максимума, т. е. вершины, все соседние вершины которой имеют меньшее целевое значение. Поскольку допустимая область является выпуклой, а целевая функция линейна, локальный оптимум в действительности является глобальным. В дальнейшем мы воспользуемся понятием двойственности, чтобы показать, что решение, получен ное с помощью симплекс алгоритма, действительно оптимально. Хотя геометрическое представление позволяет наглядно проиллюстрировать операции симплекс алгоритма, мы не будем непосредственно обращаться к нему при подробном рассмотрении симплекс метода. Вместо этого мы воспользуемся алгебраическим представлением. Сначала запишем задачу линей ного программирования в канонической форме в виде набора линейных равенств. Эти линейные равенства выражают одни переменные, называемые базисными, через другие переменные, называемые небазисными. Переход от одной вершины к другой осуществляется путем замены одной из базисных переменных на неба зисную. Данная операция называется замещением и алгебраически заключается в переписывании задачи линейного программирования в эквивалентной канони ческой форме. В дальнейшем мы рассмотрим также и более сложные случаи: задачи линейного программирования, не имеющие решений; задачи, не имеющие конеч ного оптимального решения, и задачи, для которых начало координат не является допустимым решением.

Приложения линейного программирования Линейное программирование имеет широкий спектр приложений. В любом учебнике по исследованию операций содержится множество примеров задач ли нейного программирования; линейное программирование – стандартный метод, который преподается студентам большинства школ бизнеса. Разработка сцена рия предвыборной борьбы – лишь один типичный пример. Приведем еще два примера, где с успехом используется линейное программирование. Авиакомпания составляет график работы экипажей. Федеральное авиаци онное агентство установило ряд ограничений, таких как ограничение вре мени непрерывной работы для каждого члена экипажа и требование, чтобы каждый конкретный экипаж работал только на самолетах одной модели на протяжении одного месяца. Авиакомпания хочет назначить экипажи на все рейсы, задействовав как можно меньше сотрудников (членов экипажей). Нефтяная компания выбирает место бурения скважины. С размещением буровой в каждом конкретном месте связаны определенные затраты и ожи даемая прибыль в виде некоторого количества баррелей добытой нефти, рассчитанная на основе проведенных геологических исследований. Сред ства, выделяемые на бурение новых скважин, ограничены, и компания хо чет максимизировать ожидаемое количество добываемой нефти исходя из заданного бюджета. Задачи линейного программирования также полезны при моделировании и ре шении задач теории графов и комбинаторных задач. Покажем также, как сформулировать в виде задач линейного программирования некоторые задачи теории графов и задачи сетевых потоков.

Алгоритмы решения задач линейного программирования В данном разделе мы рассмотрим симплекс алгоритм. При правильном применении данный алгоритм на практике обычно позволяет быстро решать задачи линейного программирования общего вида. Однако при некоторых специально подобранных начальных значениях время выполнения симплекс алгоритма может оказаться экспоненциальным. Первым алгоритмом с полиномиальным временем выполнения для решения задач линейного программирования был эллипсоидный алгоритм, который на практике работает весьма медленно. Второй класс полиномиальных по времени алгоритмов содержит так называемые методы внутренней точки (interior point methods). В отличие от симплекс алгоритма, который движется по границе допустимой области и на каждой итерации рассматривает допустимое решение, являющееся вершиной симплекса, эти алгоритмы осуществляют движе ние по внутренней части допустимой области. Промежуточные решения являются допустимыми, но не обязательно находятся в вершинах симплекса, однако конеч ное решение является вершиной. ля задач большой Д размерности производительность алгоритмов внутренней точки может быть сравнима с производительностью симплекс алгоритма, а иногда и превышает ее. Если ввести в задачу линейного программирования дополнительное требо вание, чтобы все переменные принимали целые значения, получится задача це лочисленного линейного программирования. В этом случае даже задача поиска допустимого решения является NP полной; поскольку ни для одной NP полной задачи не известны полиноми альные алгоритмы решения, для задач целочисленного линейного программиро вания полиномиальные по времени алгоритмы также не известны. В отличие от них, задача линейного программирования общего вида может быть решена за полиномиальное время.

Иногда удобно записывать задачу линейного программирования в более компактной форме. Определим m n матрицу А = (aij), m мерный вектор b = (bj), n мерный вектор с = (cj) и n мерный вектор x = (xj); тогда задачу линейного программирования (16) ( 18) можно запи сать в следующем виде: Максимизировать с. Тх (19) при условиях Ах ≤ b, (20) х ≥ 0. (21) В выражении (19) стх – это скалярное произведение двух векторов. В выра жении (20) Ах – произведение матрицы и вектора, а х ≥ 0 в (21) означает, что все компоненты вектора х должны быть неотрицательными. Таким образом, задачу линейного программирования в стандартной форме можно описать с по мощью тройки(A, b, с), и мы примем соглашение, что A, b и с всегда имеют указанную выше размерность.

Теперь введем терминологию для описания различных ситуаций, возника ющих в линейном программировании. Некоторые термины уже использовались в двумерной задаче. Набор значений переменных х, которые удовлетворяют всем ограничениям, называется допустимым решением, в то время как набор значе ний переменных х, не удовлетворяющий хотя бы одному ограничению, называ етсянедопустимым решением. Решению х соответствует целевое значение стх. Допустимое решение х, целевое значение которого является максимальным среди всех допустимых решений, является оптимальным решением, а его целевое зна чение с. Тх называется оптимальным целевым значением. Если задача линейного программирования не имеет допустимых решений, она называется неразрешимой, в противном случае она является разрешимой. Если задача линейного программирования имеет допустимые решения, но не имеет конечного оптимального целевого значения, она называется неограниченной.

Преобразование задач линейного программирования в стандартную форму Любую задачу линейного программирования, в которой требуется минимизи ровать или максимизировать некую линейную функцию при наличии линейных ограничений, можно преобразовать в стандартную форму. Исходная задача может находиться не в стандартной форме по четырем причинам. 1. Целевая функция минимизируется, а не максимизируется. 2. На некоторые переменные не наложены условия неотрицательности. 3. Некоторые ограничения имеют форму равенств, т. е. имеют знак равенства вместо знака "меньше или равно". 4. Некоторые ограничения неравенства вместо знака "меньше или равно" име ют знак "больше или равно". Преобразовывая задачу линейного программирования L в другую задачу ли нейного программирования L', мы бы хотели, чтобы оптимальное решение задачи L' позволяло найти оптимальное решение задачи L. Будем говорить, что две зада чи максимизации. L и L' эквивалентны, если для каждого допустимого решения х задачи L с целевым значением z существует соответствующее допустимое ре шениех' задачи L' с целевым значением z, а для каждого допустимого решения х' задачи L' с целевым значением z существует соответствующее допустимое решение х задачи L с целевым значением z. (Это определение не подразумева ет взаимно однозначного соответствия между допустимыми решениями. ) Задачи минимизации L и задача максимизации L' эквивалентны, если для каждого допу стимого решениях задачи L с целевым значением z существует соответствующее допустимое решение х' задачи L' с целевым значением z, а для каждого допусти мого решениях' задачи L' с целевым значением z существует соответствующее допустимое решение х задачи L с целевым значением z.

Покажем, как поочередно избавиться от перечисленных выше проблем. После устранения каждого несоответствия стандартной форме докажем, что новая задача линейного программирования эквивалентна старой. 1. Чтобы превратить задачу минимизации L в эквивалентную ей задачу максими зации ', достаточно просто изменить знаки коэффициентов целевой функции L на противоположные. Поскольку L и L' имеют одинаковые множества допустимых решений и для любого допустимого решения целевое значение L противоположно целевому значению L', эти две задачи линейного программирования эквивалент ны. Например, пусть исходная задача имеет вид: Минимизировать 2 x 1+ 3 x 2 при условиях x 1 + x 2 = 7 x 1 2 x 2 ≤ 4 x 1 ≥ 0 Если мы поменяем знаки коэффициентов целевой функции, то получим следую щую задачу: Максимизировать 2 x 1 3 x 2 при условиях x 1 + x 2 = 7 x 1 2 x 2 ≤ 4 x 1 ≥ 0

2. Покажем, как преобразовать задачу линейного программирования, в ко торой на некоторые переменные не наложены ограничения неотрицательности, в задачу, где все переменные подчиняются этому условию. Предположим, что для некоторой переменной xj ограничение неотрицательности отсутствует. Заменим все вхождения переменной xj выражением x'j x''j и добавим ограничения неот рицательности 'j ≥ 0 и x''j≥ 0. Так, если x целевая функция содержит слагаемое cjxj, то оно заменяется на cjx'j - cjx''j , а если ограничение i содержит слагаемое aijxj, оно заменяется на aijx'j aijx''j. Любое допустимое решение х новой зада чи линейного программирования соответствует допустимому решению исходной задачи с xj = x'j x''j и тем же самым целевым значением, следовательно, эти две задачи эквивалентны. Применив эту схему преобразования ко всем переменным, для которых нет ограничений неотрицательности, получим эквивалентную задачу линейного программирования, в которой на все переменные наложены ограниче ния неотрицательности. Продолжая рассмотрение нашего примера, проверяем, для всех ли переменных есть соответствующие ограничения неотрицательности. Для переменной х1 такое ограничение есть, а для переменной х2 – нет. Заменив переменную х2 двумя переменными х'2 и х''2 и выполнив соответствующие преобразования, получим следующую задачу: Максимизировать 2 х1 - З х'2 + З х''2 при условиях х1+ х'2 х''2 = 7 х1 – 2 х'2 + 2 х''2 ≤ 4 (22) x 1, х'2 , х''2 ≥ 0

4. Изменим знак ограничения (23). Для единообразия имен переменных переименуем х'2 в х2, и х''2 в х3. Полученная стандартная форма имеет вид: Максимизировать 2 х1 - З х2 + З х3 (24) при условиях х1+ х2 х3 ≤ 7 (25) - х1 х2 + х3 ≤ 7 (26) х1 – 2 х2 + 2 х3 ≤ 4 (27) x 1, х2 , х3 ≥ 0 (28)

(34) (35) (36) (37)

Для задачи, заданной формулами (24) (28), введя вспомогатель ные переменные x 4, x 5, x 6, получим: Максимизировать 2 х1 - 3 x 2 + Зх3 (33) при условиях x 4 = 7 – x 1 x 2 + x 3 x 5 = – 7 + x 1 + x 2 – x 3 x 6 = 4 – x 1 + 2 x 2 – 2 x 3 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0 В этой задаче линейного программирования все ограничения, за исключением условий неотрицательности, являются равенствами, и все переменные подчиня ются ограничениям неотрицательности. В записи каждого ограничения равенства в левой части стоит одна переменная, а остальные переменные находятся в пра вой части. Более того, каждое уравнение содержит в правой части одни и те же переменные, и это только те переменные, которые входят в целевую функ цию. Переменные, находящиеся в левой части равенств, называются базисными переменными (basic variables), а переменные, находящиеся в правой части, — небазисными переменными (nonbasic variables).

В задачах линейного программирования, удовлетворяющих данным условиям, мы иногда будем пропускать слова "максимизировать" и "при условии", а также "ограничения неотрицательности". Для обозначения целевой функции мы будем использовать переменную z. Полученная форма записи называется ка нонической формой (slack form). Каноническая форма задачи линейного програм мирования (33)выглядит следующим образом: z = 2 х1 - 3 x 2 + Зx 3 (34) x 4 = 7 – x 1 x 2 + x 3 x 5 = – 7 + x 1 + x 2 – x 3 x 6 = 4 – x 1 + 2 x 2 – 2 x 3 Для канонической формы, как и для стандартной, удобно иметь более ко роткий способ записи. Как будет показано в дальнейшем, множества базисных и небазисных переменных будут меняться в процессе работы симплекс алгоритма.

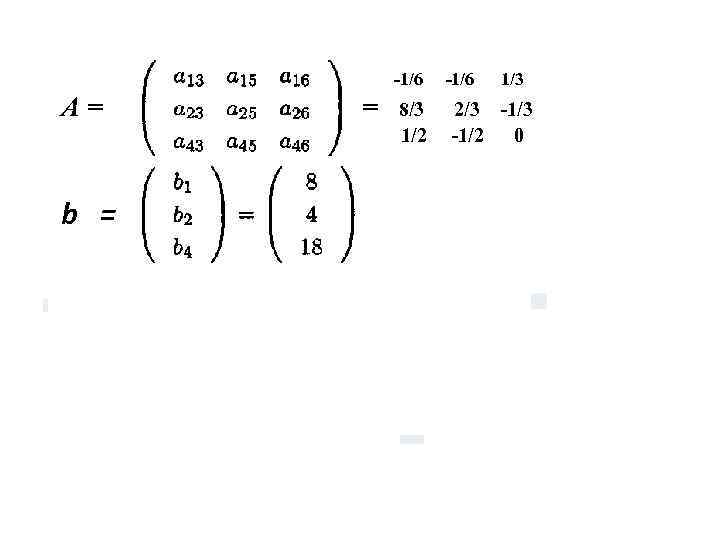1/6 A= b = = 8/3 1/2 1/6 1/3 2/3 1/2 0

с = (с3 c 5 c 6) T = ( 1/6 2/3)T , а индексы у A, b и с не обязатель но являются множествами последовательных целых чисел; они зависят от того, какие индексы входят во множества В и N. В качестве примера противополож ности элементов матрицы А коэффициентам канонической формы, заметим, что в уравнение для х1 входит слагаемое x 3/6, так что коэффициент а 13 равен 1/6, а не +1/6.

1. Если записать задачу линейного программирования (24) (28) в ком актной форме (19} (21), чему будут равны п п, m, A, b и с? 2. Укажите три допустимых решения задачи линейного программирования (24) (28). Чему равно целевое значение для каждого решения? 4. Приведите следующую задачу линейного программирования к стандарт ой форме: н Минимизировать 2 х1 + 7 x 2 при условиях х1 = 7 3 х1 + х2 ≥ 24 х1 ≥ 0 х2 ≤ 0 5. Преобразуйте следующую задачу линейного программирования в кано ическую форму: н Максимизировать 2 х1 6 x 3 при условиях х1 + x 2 x 3 ≤ 7 3 x 1 x 2 ≥ 8 - 2 xi + Х 2 -1 -x 1 + 2 х2 + 2 х3 ≥ 0 — Х — 2 x 1 , х2 , х3 ≥ 0 2 x 2 Х , > 0 Какие переменные являются базисными, а какие небазисными? Х 2 6. Покажите, что следующая задача линейного программирования является неразрешимой: Максимизировать 3 x 1 2 x 2 при условиях х1 + x 2 ≤ 2 2 x 1 2 х2 ≤ -10 x 1 , х2 ≥ 0 8. Пусть имеется задача линейного программирования общего вида с n переменными и m ограничениями. Предположим, что мы преобразовали ее в стандартную форму. Укажите верхнюю границу числа переменных и ограничений в полученной задаче. 9. Приведите пример задачи линейного программирования, для которой до пустимая область является неограниченной, но оптимальное целевое зна чение конечно.

Формулирование задач в виде задач линейного программирования Хотя основное внимание в данной главе уделяется симплекс алгоритму, важно также понимать, в каких случаях задачу можно сформулировать в виде задачи ли нейного программирования. После того как задача сформулирована в таком виде, ее можно решить за полиномиальное время с помощью эллипсоидного алгорит ма, или алгоритма внутренней точки. Существует несколько пакетов прикладных программ, эффективно решающих задачи линейного программирования, а значит, если проблему удастся сформулировать в виде задачи линейного программирова ния, то ее можно решить на практике с помощью такого пакета. Рассмотрим несколько конкретных примеров задач линейного программиро вания. Начнем с уже рассмотренной ранее задачи поиска кратчайших путей из одной вершины (single source shortest parts problem).

Кратчайшие пути Задачу поиска кратчайших путей из одной вершины источника можно сформулировать в виде задачи линейного программирования. Остановимся на формулировании задачи кратчайшего пути для одной пары источник адресат. В задаче поиска кратчайшего пути для одной пары источник адресат нам дан взвешенный ориентированный граф G = (V, Е), весовая функция w : Е → R, ставящая в соответствие дугам графа действительные веса, исходная вершина s и конечная вершина t. Мы хотим вычислить значение d[t], которое являет ся весом кратчайшего пути изs в t. Чтобы записать эту задачу в виде задачи линейного программирования, необходимо определить множество переменных и ограничения, которые позволят определить, какой путь из s в t является крат чайшим. К счастью, алгоритм Беллмана Форда именно для этого и предназначен. Когда алгоритм Беллмана Форда завершает свою работу, для каждой вершины v оказывается вычисленным значение d[v], такое что для каждой дуги (u, v) ∊ Е выполняется условие d[v] ≤ d[u] + w(u, v). Исходная вершина первоначально получает значение d[s]= 0, которое никогда не изменяется. Таким образом, мы получаем следующую задачу линейного программирования для вычисления веса кратчайшего пути из s в t: Максимизировать d[t] при условиях d [v/] ≤ d [u] + w (и, v) для всех (u, v)∊ Е, d[s] =0. В этой задаче |V | переменных d [v], по одной для каждой вершины v∊ Е, и |Е| + + 1 ограничение, по одному для каждой дуги плюс дополнительное ограничение, состоящее в том, что исходной вершине всегда соответствует значение 0.

Симплекс алгоритм является классическим методом решения задач линейно го программирования. В отличие от многих ранее рассмотренных алгоритмов, время выполнения этого алгоритма в худшем случае не является полиномиальным. Однако он действительно выражает суть линейного програм мирования и на практике обычно бывает достаточно быстрым. Симплекс алгоритм имеет геометрическую интерпретацию, описанную ранее в данной главе, кроме того, можно провести определенные аналогии между ним и методом исключения Гаусса. Метод исключения Гаусса применяется при поиске решения системы линейных уравнений. На каж дой итерации система переписывается в эквивалентной форме, имеющей опреде ленную структуру. После ряда итераций получается система, записанная в таком виде, что можно легко найти ее решение. Симплекс алгоритм работает анало гичным образом, и его можно рассматривать как метод исключения Гаусса для неравенств.

Пример симплекс алгоритма Рассмотрим следующую задачу линейного программирования в стандартной форме: Максимизировать 3 х1+ х2 + 2 х3 при условиях х1+ х2 + 3 х3 ≤ 30 2 х1+ 2 х2 + 5 х3≤ 24 4 х1+ х2 + 2 х3 ≤ 36 х1, х2, х3 ≥ 0. . Чтобы можно было применить симплекс алгоритм, необходимо преобразо вать данную задачу в каноническую форму. Вспомо гательные переменные − не просто элементы алгебраического преобразования, они являются содержательным алгоритмическим понятием. Будем говорить, что ограничение равенство является строгим (tight) при опреде ленном наборе значений его небазисных переменных, если при этих значениях базисная переменная данного ограничения становится равной 0. Аналогично, на бор значений небазисных переменных, который делает базисную переменную отрицательной, нарушает данное ограничение. Таким образом, вспомогательные переменные наглядно показывают, насколько каждое ограничение отличается от строгого, и тем самым помогают определить, насколько можно увеличить значе ния небазисных переменных, не нарушив ни одного ограничения.

Опишем основную идею, лежащую в основе итераций симплекс алгоритма. С каждой итерацией связывается некое "базисное решение", которое легко по лучить из канонической формы задачи линейного программирования: каждой небазисной переменной присваивается значение 0, и из ограничений равенств вычисляются значения базисных переменных. Базисное решение всегда соответ ствует некой вершине симплекса. С алгебраической точки зрения каждая итерация преобразует одну каноническую форму в эквивалентную. Целевое значение, соот ветствующее новому базисному допустимому решению, должно быть не меньше (как правило, больше) целевого значения предыдущей итерации. Чтобы добиться этого увеличения, выбирается некоторая небазисная переменная, причем такая, что при увеличении ее значения целевое значение также увеличится. То, насколь ко можно увеличить данную переменную, определяется другими ограничениями; а именно: ее значение увеличивается до тех пор, пока какая либо базисная пере менная не станет равной 0. После этого каноническая форма переписывается так, что эта базисная переменная и выбранная небазисная переменная меняются ро лями. Хотя мы использовали определенные начальные значения переменных для описания алгоритма и будем использовать их в наших доказательствах, в алго ритме данное решение в явном виде не поддерживается. Он просто переписывает задачу линейного программирования до тех пор, пока оптимальное решение не станет "очевидным".

Свяжем с приведенными ограничениями вспомогательные переменные х4, х5 и. х6, соответственно, и приведем задачу линейного программирования к канони ческой форме. В результате получится следующая задача: z = 3 х1+ х2 + 2 х3 х4 = 30 х1 - х2 - 3 х3 х5 = 24 2 х1 2 х2 - 5 х3 х6 = 36 - 4 х1 - х2 - 2 х3 Система ограничений содержит 3 уравнения и 6 переменных. Лю бое задание значений переменных х1, х2, х3 определяет значения переменных х4, х5, х6 , следовательно, существует бесконечное число решений данной систе мы уравнений. Решение является допустимым, если все х1, х2, х3, х4, х5, х6 неотрица тельны. Число допустимых решений также может быть бесконечным. Рассмотрим базисное решение (basic solution): установим все (небазисные) переменные правой части равными 0 и вычислим значения (базисных) переменных левой части. В данном примере базисным ре шением является(х1, х2, х3, х4, х5, х6 ) = (0, 0, 0, 30, 24, 36) и ему соответствует целевое значение z = (3 • 0) + (1 • 0) + (2 • 0) = 0. Заметим, что в этом базисном реше нии i =bi x для всех i ∊ В. Итерация симплекс алгоритма переписывает множе ство уравнений и целевую функцию так, что в правой части оказывается другое множество переменных. Таким образом, с переписанной задачей связано другое базисное решение. Мы подчеркиваем, что такая перезапись никоим образом не меняет лежащую в основе задачу линейного программирования; задача на каж дой итерации имеет точно то же множество допустимых решений, что и задача на предыдущей итерации. Однако эта задача имеет базисное решение, отличное от базисного решения предыдущей итерации.

Продолжая изучение примера, рассмотрим возможность увеличения значения х1. При увеличении х1 значения переменных х4, х5, х6 уменьшаются. Поскольку на каждую переменную наложено ограничение неотрицательности, ни одна из этих переменных не должна стать отрицательной. Если х1 увеличить более, чем на 30, то х4 станет отрицательной, а х5 и х6 станут отрицательными при увеличении х1 на 12 и 9 соответственно. Третье ограничение является самым строгим, именно определяет, на сколько можно увеличить х1. Следовательно, поменяем ролями переменные х1 и х6 Решим уравнение относительно х1 и получим x 1 = 9 x 2/4 x 3/2 x 6/4 Чтобы записать другие уравнения с x 6 в правой части, подставим вместо x 1 это выражение. Поступая далее аналогичным образом, получаем нашу задачу линейного программирования в виде: z = 27 + x 2/4 + x 3/2+ 3 x 6/4 x 1 = 9 x 2/4 x 3/2 x 6/4 x 4 = 21 3 x 2/4 5 x 3/2+ x 6/4 x 5 = 6 3 x 2/2 4 x 3+ x 6/2 Эта операция называется замещением. Как было показано выше, в процессе заме щения выбираются небазисная переменнаяхе, называемая вводимой переменной (entering variable), и базисная переменная хk называемая выводимой переменной (leaving variable), которые затем меняются ролями.

Полученная задача эквивалентна исходной задаче. В процессе работы симплекс алгоритма производятся только операции переноса переменных из левой части уравнения в правую и наоборот, а также подстановки одного уравнения в другое. Первая операция, очевидно, создает эк вивалентную задачу, то же можно сказать и о второй операции. Чтобы продемонстрировать эквивалентность указанных задач, убедимся, что исходное базисное решение (0, 0, 0, 30, 24, 36) удовлетворяет новым уравнениям И имеет целевое значение 27 + (1/4) • 0 + (1/2) • 0 (3/4) • 36 = 0. В базисном решении, связанном с новой задачей, новые небазисные переменные равны 0. Таким образом, оно имеет вид (9, 0, 0, 21, 6, 0), а соответствующее це левое значение = 27. Простые z арифметические действия позволяют убедиться, что данное решение удовлетворяет уравнениям исходной задачи и при подстановке в целевую функцию имеет целевое значение (3 • 9) + (1 • 0) + (2 • 0) = 27.

Продолжая рассмотрение примера, необходимо найти новую базисную пере менную, значение которой можно увеличить. Нет смысла увеличиватьx 6, по скольку при ее увеличении целевое значение уменьшается. Можно попробовать увеличить x 2 или x 3; мы выберем x 3. Насколько можно увеличить x 3, чтобы не нарушить ни одно из ограничений? Ограничение для x 1 допускает увеличение, не превышающее 18, ограничение для x 4 – 42/5, а ограничение для x 5 − 3/2. Третье ограничение снова оказывается самым строгим, следовательно, мы пере писываем его так, чтобы x 3 было в левой части, а x 5 − в правой части. Затем подставляем это новое уравнение в уравнения и получаем новую эквивалентную задачу: z = 111/4 + x 2/16 x 5/8 11 x 6/16 x 1 = 33/4 x 2/16 + x 5/8 5 x 6/16 x 4 = 3/2 3 x 2/8 x 5/4+ x 6/8 x 5 = 69/4 + 3 x 2/16 +5 x 5/8 x 6/16 С этой системой связано базисное решение (33/4, 0, 3/2, 69/4, 0, 0) с целевым зна чением 111/4. Теперь единственная возможность увеличить целевое значение − увеличить x 2. Имеющиеся ограничения задают верхние границы увеличения 132, 4 и оо соответственно (верхняя граница в ограничении равна оо, посколь ку при увеличении x 2 значение базисной переменной x 4 также увеличивается. Следовательно, данное уравнение не налагает никаких ограничений на величину возможного увеличения x 2) Увеличиваем x 2 до 4 и делаем ее базисной.

Затем решаем уравнение относительно x 2, подставляем полученное выражения в другие уравнения и получаем новую задачу: z = 28 x 3/6 x 5/6 2 x 6/3 x 1 = 8 + x 3/6 + x 5/6 x 6/3 x 2 = 4 9 x 3/3 2 x 5/3+ x 6/3 x 4 = 18 x 3/2 +x 5/2 В полученной задаче все коэффициенты целевой функции отрицательны. Как будет показано далее, такая ситуация возникает только тогда, когда базисное ре шение переписанной задачи линейного программирования является оптимальным ее решением. Таким образом, для данной задачи решение (8, 4, 0, 18, 0, 0) с целе вым значением 28 является оптимальным. Теперь можно вернуться к исходной задаче линейного программирования, заданной уравнениями. Ис ходная задача содержит только переменные х1, х2, х3, поэтому оптимальное решение имеет вид х1= 8, x 2 = 4, х3= 0, с целевым значением (3 • 8) + (1 • 4) + + (2 • 0) = 28. Заметим, что значения вспомогательных переменных в окончатель ном решении показывают, насколько велик резерв в каждом неравенстве. Вспомо гательная переменная 4 равна 18, а значение x левой части в неравенстве равно 8 + 4 + 0= 12, что на 18 меньше, чем значение правой части этого нера венства − 30. Вспомогательные переменныех5 и х6 равны 0, и действительно, в неравенствах левые и правые части равны. Обратите внимание на то, что даже если коэффициенты исходной канонической формы являются це лочисленными, коэффициенты последующих эквивалентных задач не обязательно целочисленны, и не обязательно целочисленны и промежуточные решения. Более того, окончательное решение задачи линейного программирования не обязательно будет целочисленным; в данном примере это просто совпадение.

коэффициентам канонической формы. ) PIVOT (N, В, А, b, с, v, k, e) 1. //Вычисление коэффициентов уравнения //для новой базисной переменной хе 2 be’ bk/ake 3 for (для) всех j ∊ N − {е} 4 do aej’ akj/ake 5 aek 1/ ake 6 > Вычисление коэффициентов остальных ограничений 7 for (для) всех i ∊ В − {k} 8 do bi’ bi − aie bе’ 9 for (для) всех j ∊ N − {е} 10 do aij’ aij − aie aej’ 11 aik’ −aieaek’ 12 > Вычисление целевой функции 13 v’ v+ cebe’ 14 for (для) всех j ∊ N - {e} 15 do cj − ceaej’ 16 ci’ −ceaek’ 17 > Вычисление новых множеств базисных и небазисных переменных 18 N’ N {e}U{k} 19 B’ B {k}U{e} 20 return (N’, В’, А’, b’, с’, v’)

Процедура PIVOT работает следующим образом. В строках 1 4 вычисляют ся коэффициенты нового уравнения для хе; для этого уравнение, в левой части которого стоит xk, переписывается так, чтобы в левой части оказалась хе. В стро ках 7 11 оставшиеся уравнения обновляются путем подстановки правой части полученного нового уравнения вместо всех вхождений хе. В строках 13 16 такая же подстановка выполняется для целевой функции, а в строках 18 и 19 обновляют ся множества небазисных и базисных переменных. Строка 20 возвращает новую каноническую форму. Если ake = 0, вызов процедуры PIVOT приведет к ошибке (деление на 0), однако, данная процедура вызывается только тогда, когда ake ≠ 0.

Формальный симплекс алгоритм Теперь мы готовы формализовать симплекс алгоритм, который уже продемонстрировали на примере. Этот пример был очень удачным, однако нам еще необходимо ответить на следующие вопросы. Как определить, что задача линейного программирования является разре шимой? Что делать, если задача линейного программирования является разрешимой, однако начальное базисное решение не является допустимым? Как определить, что задача линейного программирования является неогра ниченной? Как выбирать вводимую и выводимую переменные? Предположим, что у нас есть процедура INITIALIZE_SIMPLEX(A, b, с), которая получает на входе задачу линейного программирования в стандартной форме, т. е. матрицу А = (аij) раз мером m n т мерный вектор b = (bi) и n мерный вектор с = (ci). Если задача неразрешима, процедура возвращает соответствующее сообщение и завершается. В противном случае она возвращает каноническую форму, начальное базисное решение которой является допустимым. Процедура SIMPLEX получает на входе задачу линейного программирования в стандартной форме, описанной выше. Она возвращает n мерный вектор х = (xj), который является оптимальным решением задачи линейного программи рования, заданной формулами (29. 19) (29. 21).

Simplex (A, B, С) 1. (N, В, А, b, с, v) INITIALIZE_SIMPLEX(A, b, с) 2. while (пока) cj > 0 для некоторого индекса j ∊ N 3. do выбрать индекс е ∊ N, для которого се > 0 4. for (для) каждого индекса i ∊ В 5. do if aie > 0 6. then Di b/aie 7. else Di оо 8. Выбираем индекс k ∊ В, который минимизирует Di 9. if Di = оо 10. then return "Задача неограниченна“ 11. else (N, B, A, b, c, v) PIVOT(N, В, А, b, с, v, k, e) 12. for i to n 13. do if i∊ В 14. then xi ’ bi 15. else xi ’ 0 16. return (х1’ , x 2, ’. . . , xn’)

Процедура SIMPLEX работает следующим образом. В строке 1 выполняется вы зов упомянутой выше процедуры INITIALIZE_SIMPLEX(A, b, с), которая или опреде ляет, что предложенная задача неразрешима, или возвращает каноническую фор му, базисное решение которой является допустимым. Главная часть алгоритма со держится в цикле hile в строках 2 11. Если все w коэффициенты целевой функции отрицательны, цикл while завершается. В противном случае в строке 3 мы выби раем в качестве вводимой переменной некоторую переменную хе, коэффициент при которой в целевой функции положителен. Хотя в качестве вводимой мож но выбирать любую такую переменную, предполагается, что используется некое предварительно заданное детерминистическое правило. Затем, в строках 4 8, про изводится проверка каждого ограничения и выбирается то, которое более всего лимитирует величину увеличения хе, не приводящего к нарушению ограниче ний неотрицательности; базисная переменная, связанная с этим ограничением, выбирается в качестве хk. Если таких переменных несколько, можно выбрать любую из них, однако предполагается, что и здесь мы используем некое предва рительно заданное детерминистическое правило. Если ни одно из ограничений не лимитирует возможность увеличения вводимой переменной, алгоритм выдает сообщение "неограниченна" (строка 10). В противном случае, в строке 11 ро ли вводимой и выводимой переменных меняются путем вызова описанной выше процедуры Pl. V 0 T(N, В, А, b, с, v, k, e). В строках 12 15 вычисляется решение для переменных х1’, x 2, ’. . . , xn’ исходной задачи линейного программирования путем присваивания всем небазисным пере менным значения 0, а всем базисным пере менным i’ соответствующих значений bi. x

Упражнения. 1. Решите следующую задачу линейного программирования, используя про цедуру SIMPLEX: Максимизировать 18 x 1 +12. 5 x 2 при условиях x 1 +x 2 ≤ 20 x 1 ≤ 12 x 2 ≤ 16 x 1 , x 2 ≥ 0 2. Решите следующую задачу линейного программирования, используя про цедуру SIMPLEX: Максимизировать − 5 x 1 − 3 x 2 при условиях x 1 −x 2 ≤ 1 2 x 1 +x 2 ≤ 2 x 1 , x 2 ≥ 0 3. Решите следующую задачу линейного программирования, используя про цедуру SIMPLEX: Минимизировать x 1 + x 2 + x 3 при условиях 2 x 1 + 7. 5 x 2 + 3 x 3 ≥ 10000 20 x 1 + 5 x 2 + 10 x 3 ≥ 30000 x 1 , x 2 , x 3 ≥ 0

Двойственность При определенных предположениях процедура SIMPLEX за вершается. Однако еще не доказано, что она действительно находит оптимальное решение задачи линейного программирования. Чтобы сделать это, введем новое мощное понятие − двойственность (дуальность) задач линейного программи рования (linear programming duality). Двойственность − очень важное свойство. В задачах оптимизации определе ние двойственной задачи практически всегда сопровождается открытием алго ритма с полиномиальным временем выполнения. Двойственность также является очень мощным средством при доказательстве того, что решение действительно является оптимальным. Для задачи максимизации определяется связанная с ней задача минимизации, причем такая, что эти две задачи имеют одно и то же оптимальное значение. Опишем, как для заданной задачи линейного программирования, в которой требуется максимизировать целевую функцию, сформулировать двойственную (dual) задачу линейного программирования, в которой целевую функцию требу ется минимизировать и оптимальное значение которой идентично оптимальному значению исходной задачи. При работе с двойственными задачами исходная зада ча называется прямой (primal).

Для задачи линейного программирования в стандартной форме определим двойственную задачу следующим образом: Чтобы получить двойственную задачу для задачи максимизации, нужно изменить максимизацию на ми нимизацию, поменять роли коэффициентов правых частей и целевой функции и заменить неравенства "меньше или равно" на "больше или равно". С каждым из m ограничений прямой задачи в двойственной задаче связана переменная уi, а с каждым из n ограничений двойственной задачи связана переменная прямой задачи xj. Например, для рассмотренного ранее примера симплекс алгоритма двойственная задача выглядит следующим образом: Минимизировать З 0 у1 + 24 у2 + 36 у3 (прямая: Максимизировать 3 х1+ х2 + 2 х3 при условиях при условиях у1 + 2 у2 + 4 у3 ≥ 3 х1+ х2 + 3 х3 ≤ 30 у1 + 2 у2 + у3 ≥ 1 2 х1+ 2 х2 + 5 х3≤ 24 3 у1 + 5 у2 + 2 у3≥ 2 4 х1+ х2 + 2 х3 ≤ 36 у1, у2, у3 ≥ 0 х1, х2, х3 ≥ 0 ) Отметим, что оптимальное значение двойственной зада чи линейного программирования всегда равно оптимальному значению прямой задачи. Более того, симплекс алгоритм неявно решает одновременно обе задачи, прямую и двойственную, тем самым обеспечивая доказательство оптимальности

Упражнения 1. Сформулируйте двойственную задачу для задачи, приведенной в упраж нении 1. 2. Предположим, у нас есть задача линейного программирования, не при веденная к стандартной форме. Можно получать двойственную задачу в два этапа: сначала привести исходную задачу к стандартной форме, а затем формулировать двойственную. Однако было бы удобно иметь возможность сразу формулировать двойственную задачу. Объясните, ка ким образом, имея произвольную задачу линейного программирования, можно получить двойственную задачу непосредственно. 3. Покажите, что задача, двойственная к двойственной задаче линейного программирования, является прямой задачей.

Начальное базисное допустимое решение Cначала покажем, как проверить, является ли задача ли нейного программирования разрешимой, и как в случае положительного ответа получить каноническую форму, базисное решение которой является допустимым. В заключение мы докажем основную теорему линейного программирования, в ко торой утверждается, что процедура implex всегда дает правильный результат. S Поиск начального решения В алгоритме Simplex предполагалось, что у нас есть некая процедура Initialize^ Simplex, которая определяет, имеет ли задача линейного программирования до пустимые решения, и в случае положительного ответа возвращает каноническую форму, имеющую допустимое базисное решение. Опишем данную процедуру. Даже если задача линейного программирования является разрешимой, началь ное базисное решение может оказаться недопустимым. Рассмотрим, например, следующую задачу: Максимизировать 2 x 1− 3 x 2 при условиях 2 x 1 −x 2 ≤ 2 x 1 − 5 x 2 ≤ − 4 x 1 , x 2 ≥ 0

Если преобразовать эту задачу в каноническую форму, базисным решением будет х1 = 0, x 2 = 0. Это решение нарушает второе ограничение и, следователь но, не является допустимым. Таким образом, процедура INITIALIZE_SIMPLEX не может сразу возвратить эту очевидную каноническую форму. На первый взгляд, вообще неясно, имеет ли данная задача допустимые решения. Чтобы определить, существуют ли они, можно сформулировать вспомогательную задачу линейного программирования (auxiliary linear program). Для этой вспомогательной задачи мы сможем (причем достаточно легко) найти каноническую форму, базисное ре шение которой является допустимым. Более того, решение этой вспомогательной задачи линейного программирования позволит определить, является ли исходная задача разрешимой, и если да, то обеспечит допустимое решение, которым можно инициализировать процедуру SIMPLEX.

Теперь опишем стратегию поиска начального базисного допустимого решения задачи линейного программирования L, заданной в стандартной форме: Initialize_Simplex(A, b, с) Пусть k — индекс минимального коэффициента bi if bk ≥ 0 > Допустимо ли начальное базисное решение? then return ({1, 2, . . . , n}, {п + 1, n + 2, . . . , п + m}, А, b, с, 0) Образуем Laux путем добавления –х0 к левой части каждого уравнения и задаем целевую функцию равной –х0