ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 1 Алгоритм реализации 1 2

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 1

Алгоритм реализации 1. 2. 3. 4. 5. 6. Определить переменные Задать целевую функцию Выразить ограничения в форме неравенств Определить возможное пространство решений Графически определить оптимальную точку Алгебраически рассчитать переменные в оптимальной точке 7. Получить решение задачи 2

Пример Компания производит мебель двух наименований: столы и шкафы. Каждый продукт проходит через 2 цеха: столярный и полировочный цеха. Время, потраченное в каждом из цехов на единицу продукции, отражено ниже: Столы Шкафы Время на обработку (часы) Столярный цех Полировочный цех 3 2 4 6 В год каждый цех располагает 4800 рабочих часов. Ежегодная продукция столов не должна превышать 1200 единиц Чистая прибыль от продажи для столов – 100 $, для шкафов – 150 $ 3

Модель Пусть X – число столов, которые должны быть изготовлены в год; Y – число шкафов, которые должны быть изготовлены в год; C – общая прибыль от реализации Максимизация С =100 x + 150 y Ограничения: 3 х + 4 y ≤ 4800 (часы столярного цеха) 2 х + 6 y ≤ 4800 (часы полировочного цеха) х ≤ 1200 (максимальное количество столов) x ≥ 0, y ≥ 0 4

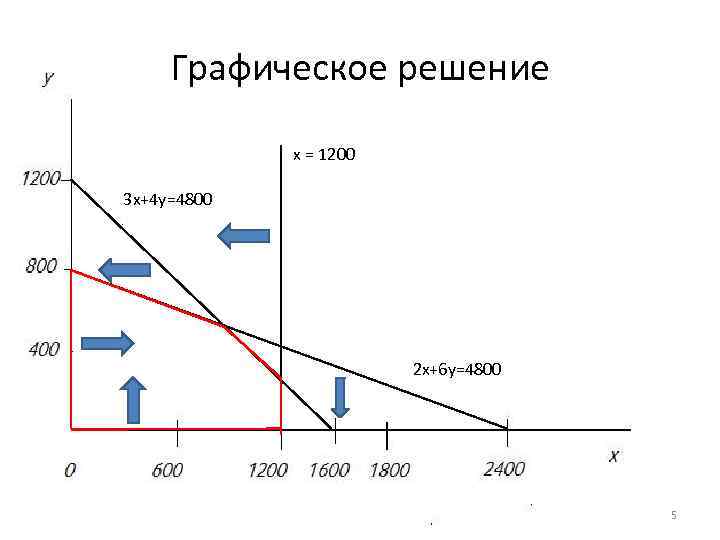Графическое решение x = 1200 3 x+4 y=4800 2 х+6 y=4800 5

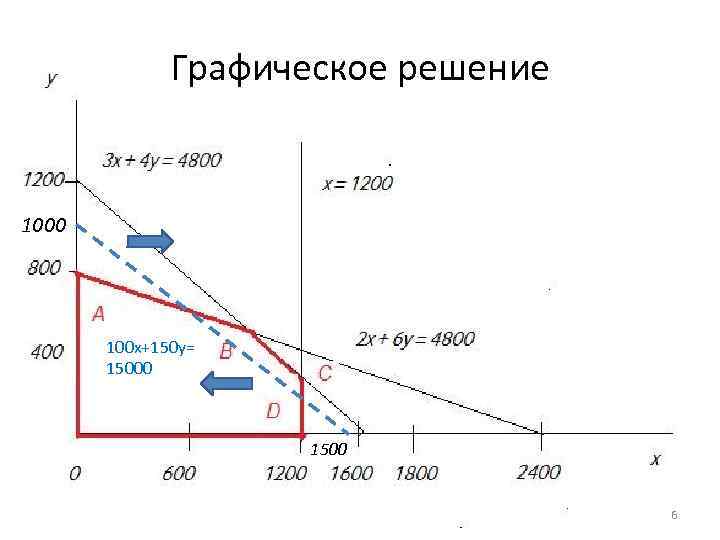Графическое решение 1000 100 x+150 y= 15000 1500 6

Алгебраическое решение Точка B является пересечением двух прямых: 3 x + 4 y = 4800 2 x + 6 y = 4800 Решая систему уравнений, находим x и у: X = 960 Y = 480 Оптимальным решением будет производить 960 столов и 480 шкафов. Это позволит максимизировать прибыль, которая составит: C = 100 x 960 + 480 x 150 = 168 000 $ 7

Решение в MS Excel Исходные данные 8

Решение в MS Excel Исходные данные 9

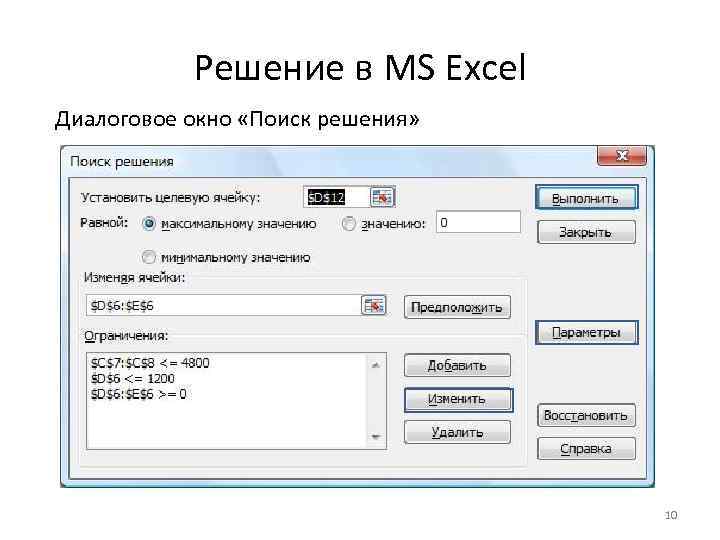Решение в MS Excel Диалоговое окно «Поиск решения» 10

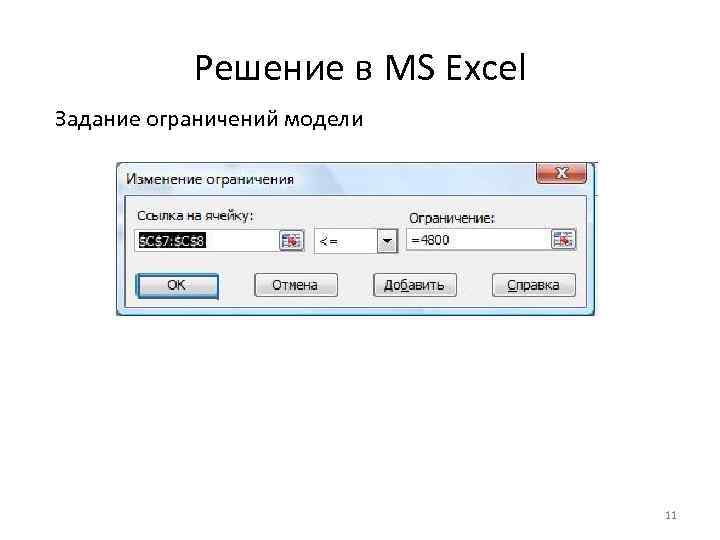Решение в MS Excel Задание ограничений модели 11

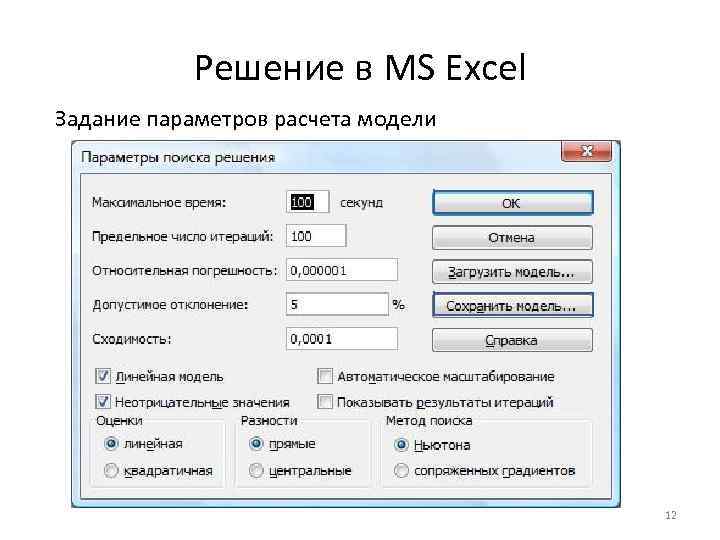Решение в MS Excel Задание параметров расчета модели 12

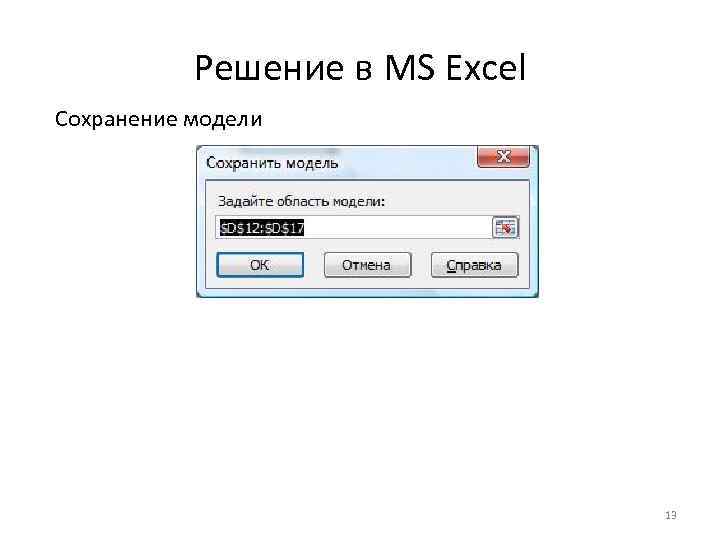Решение в MS Excel Сохранение модели 13

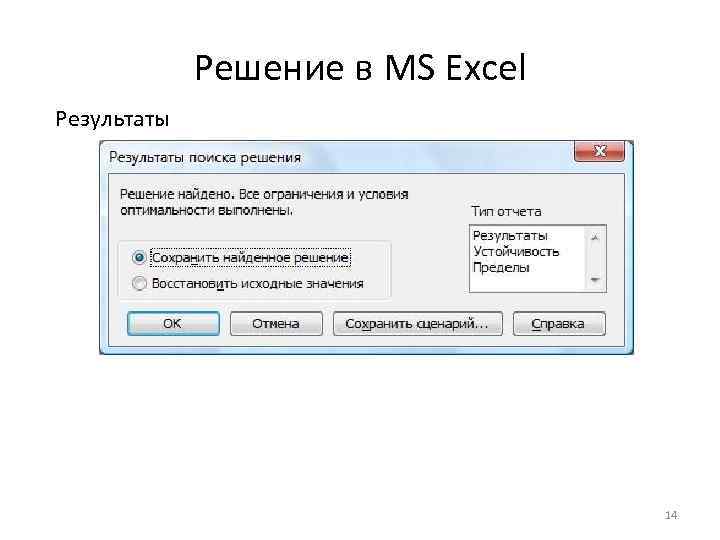Решение в MS Excel Результаты 14

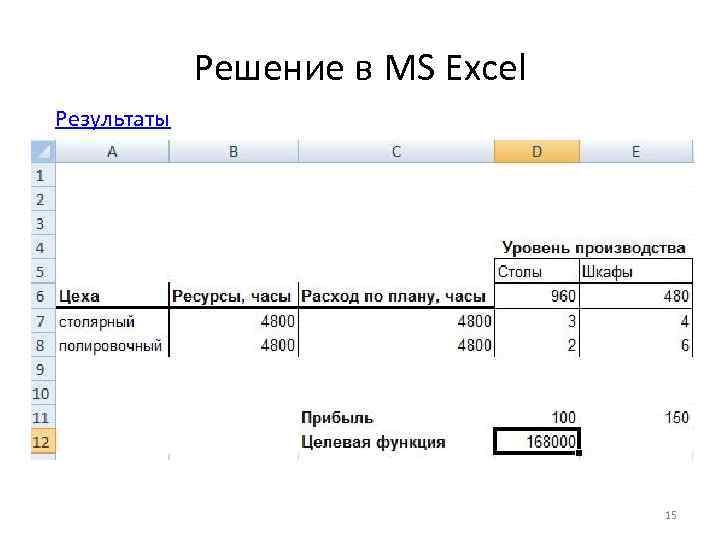Решение в MS Excel Результаты 15

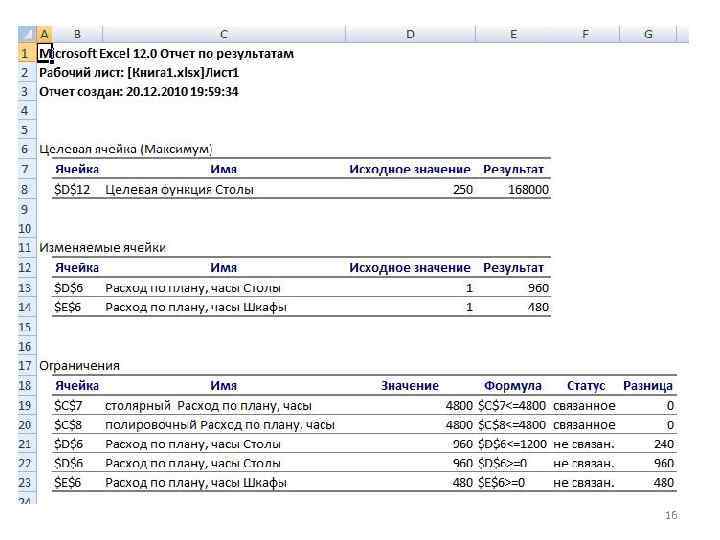16

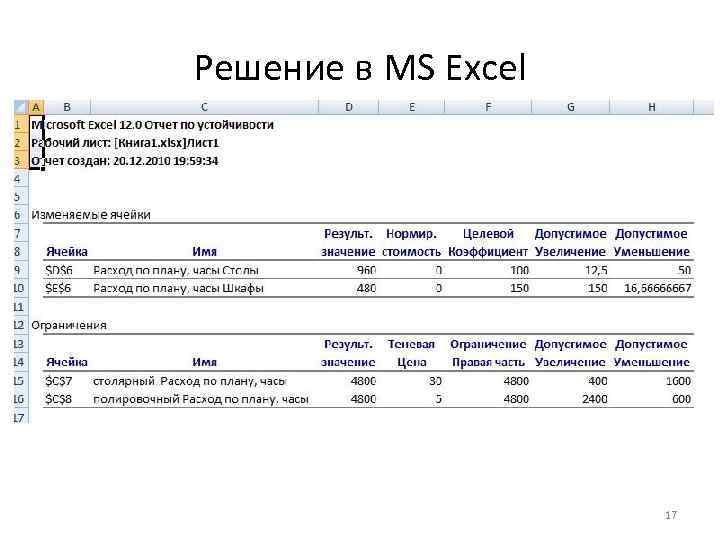Решение в MS Excel 17

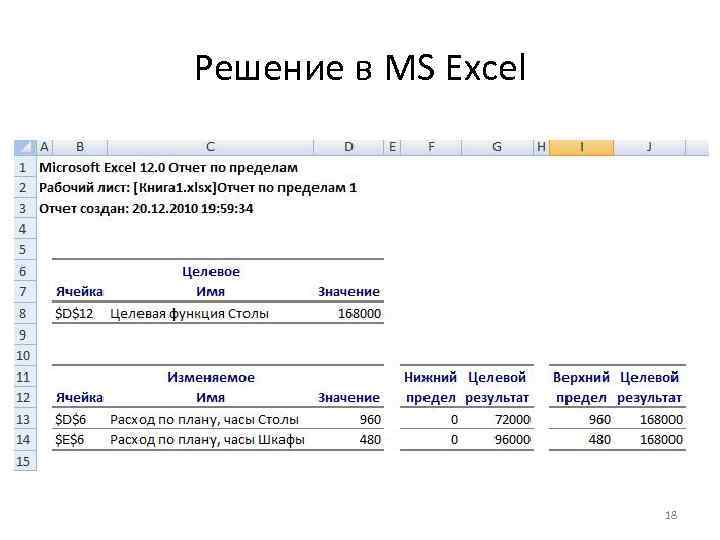Решение в MS Excel 18

Ограничения метода üЛинейность üБесконечная делимость продуктов и ресурсов üРешение может не иметь целых чисел üТолько одно решение считается оптимальным üТолько два продукта для графического решения 19