Линейная парная модель Виды зависимостей между переменными

Линейная парная модель

Виды зависимостей между переменными n n n Функциональная: каждому значению одной переменной соответствует вполне определенное значение другой; Статистическая (стохастическая, вероятностная): каждому значению одной переменной соответствует определенное (условное) распределение другой; Корреляционная: каждому значению одной переменной соответствует определенное условное математическое ожидание другой

Классическая нормальная линейная регрессионная модель Вид модели: n Основные предпосылки: 1) возмущение ε – случайная величина, переменная Х – неслучайная 2) 3) 4) возмущения не коррелированы: n 5) возмущение ε – нормально распределенная случайная величина

Линейная парная регрессия (пример) n n n Y(т) - сменная добыча угля на одного рабочего; Х(м) – мощность пласта; i – номер шахты

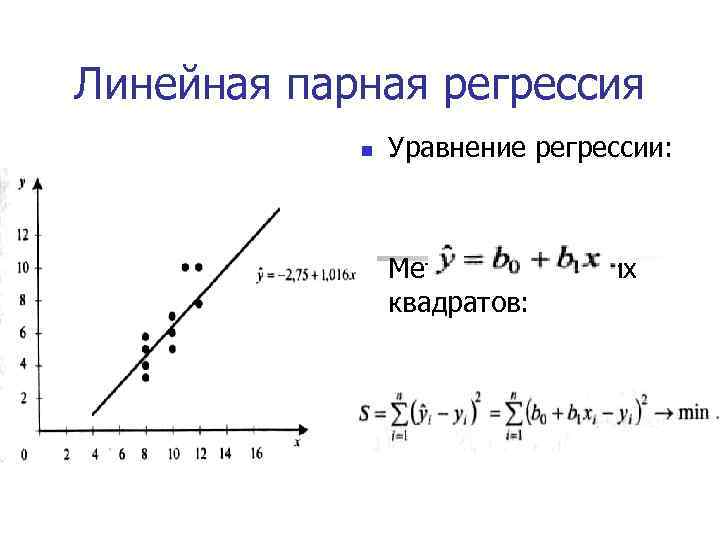Линейная парная регрессия n n Уравнение регрессии: Метод наименьших квадратов:

Линейная парная регрессия (основные формулы) n Уравнение регрессии: n Параметры уравнения: n n b 0 и b 1 – наиболее эффективные оценки для β 0 и β 1 (теорема Гаусса-Маркова) Соответствующие средние рассчитываются по формулам:

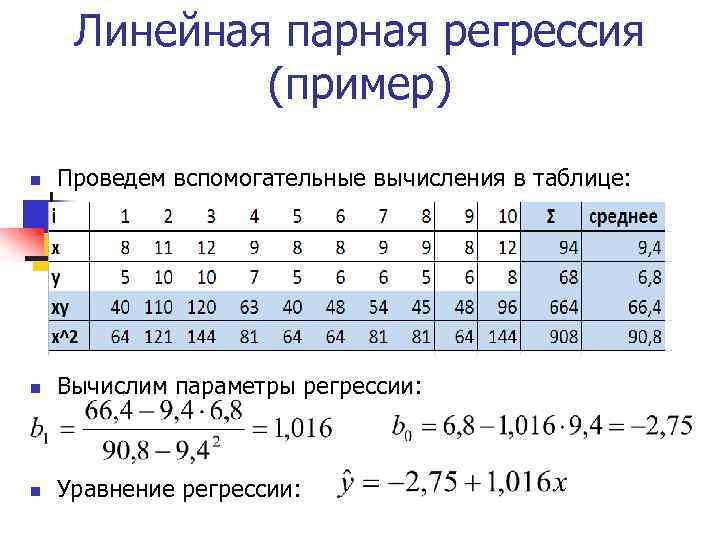Линейная парная регрессия (пример) n Проведем вспомогательные вычисления в таблице: n Вычислим параметры регрессии: n Уравнение регрессии:

СТАТИСТИЧЕСКИЙ АНАЛИЗ ЛИНЕЙНОЙ ПАРНОЙ МОДЕЛИ

I. Оценка тесноты корреляционной зависимости n Показатель тесноты линейной связи – коэффициент корреляции r:

Свойства коэффициента корреляции n Показывает, на сколько стандартных отклонений изменяется у при увеличении х на один стандарт. Принимает значения от -1 до 1 n Более детальная шкала - шкала Чэддока (по модулю r): n 0, 1 -0, 3 – связь слабая 0, 3 -0, 5 – умеренная 05, -0, 7 – заметная n 0, 7 -0, 9 – тесная 0, 9 -0, 99 – весьма тесная 1 - функциональная При r>0 связь прямая, при r<0 – обратная.

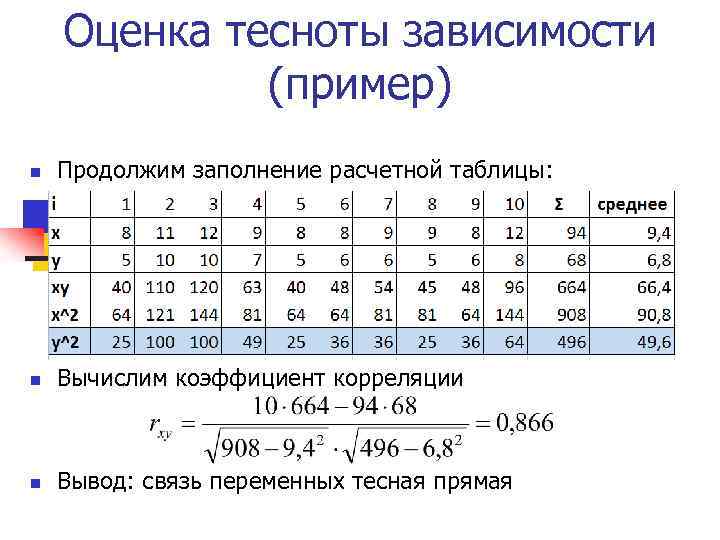Оценка тесноты зависимости (пример) n Продолжим заполнение расчетной таблицы: n Вычислим коэффициент корреляции n Вывод: связь переменных тесная прямая

II. Оценка влияния фактора на зависимую переменную n n Показатель – средний коэффициент эластичности. Показывает, на сколько процентов изменяется у при увеличении х на 1%:

Оценка влияния фактора (пример) n n Вычислим Е: Вывод: при увеличении мощности пласта на 1% сменная норма увеличивается в среднем на 1, 4%.

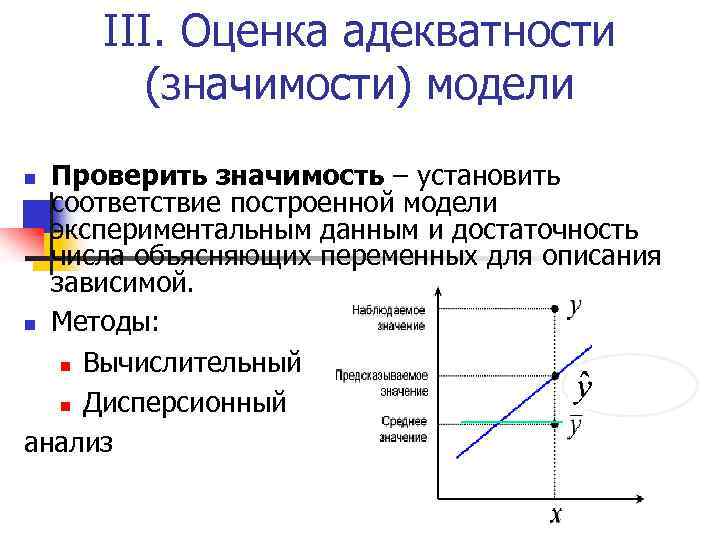III. Оценка адекватности (значимости) модели Проверить значимость – установить соответствие построенной модели экспериментальным данным и достаточность числа объясняющих переменных для описания зависимой. n Методы: n Вычислительный n Дисперсионный анализ n

3. 1. Оценка адекватности модели n n n Точность модели оценивают с помощью среднего коэффициента аппроксимации Показывает, на сколько процентов в среднем расчетные значения У отклоняются от фактических. Допустимый предел 8 -10%, максимально возможный 12 -15%.

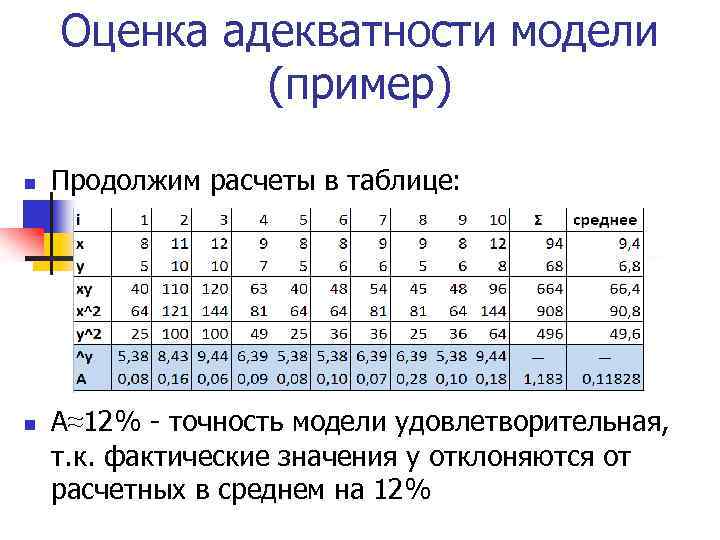Оценка адекватности модели (пример) n n Продолжим расчеты в таблице: А≈12% - точность модели удовлетворительная, т. к. фактические значения у отклоняются от расчетных в среднем на 12%

3. 2. Оценка значимости уравнения регрессии n n Идея дисперсионного анализа: оценка влияния фактора на основе анализа дисперсии отклонений (или соответствующей суммы квадратов). Обозначения: n Объяснимая вариация n Необъяснимая вариация n Общая вариация или

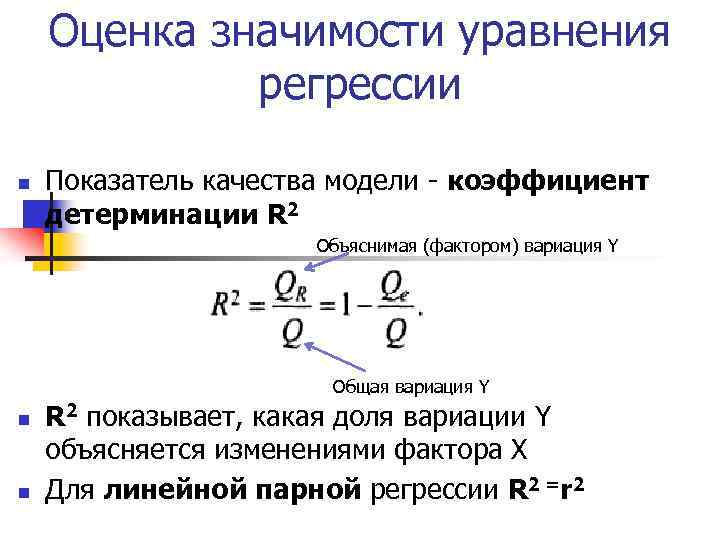Оценка значимости уравнения регрессии n Показатель качества модели - коэффициент детерминации R 2 Объяснимая (фактором) вариация Y Общая вариация Y n n R 2 показывает, какая доля вариации Y объясняется изменениями фактора Х Для линейной парной регрессии R 2 =r 2

Оценка значимости уравнения регрессии n Значимость уравнения устанавливается посредством F-теста: 1. Вычислить 2. Найти Сравнить Вывод: уравнение значимо на уровне α 3.

Оценка значимости модели (пример) n Вычислим т. е. 75% изменений сменной нормы объясняется мощностью угольного пласта, 25% - другими факторами n Проведем F-тест: n Вычислим n По таблице Фишера для α=0, 05 найдем n Fнабл>Fтабл, т. е. построенное уравнение регрессии значимо на уровне α=0, 05.

IV. Интервальная оценка параметров модели ДИ для среднего значения Мх. Y где оценка дисперсии среднего значения ДИ для индивидуального значения у*0 где оценка дисперсии индивидуального значения

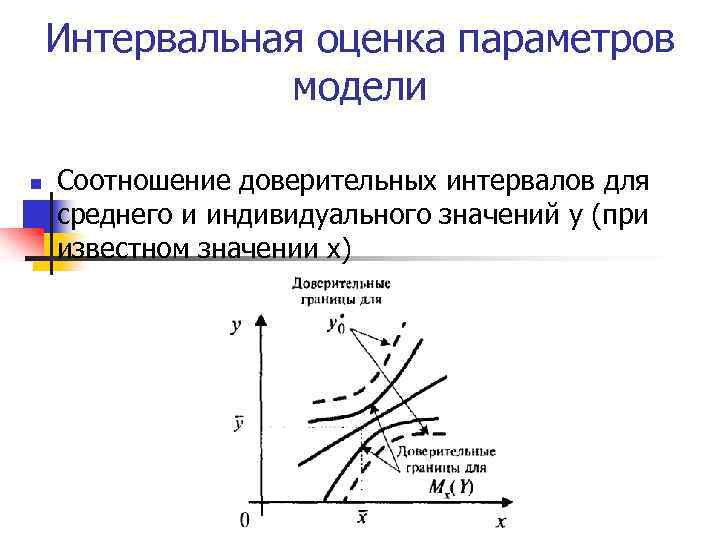Интервальная оценка параметров модели n Соотношение доверительных интервалов для среднего и индивидуального значений у (при известном значении х)

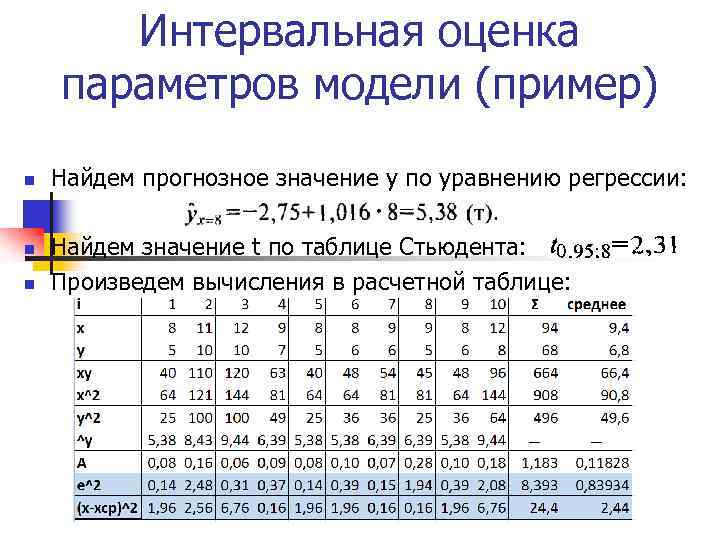Интервальная оценка параметров модели (пример) n n n Найдем прогнозное значение у по уравнению регрессии: Найдем значение t по таблице Стьюдента: Произведем вычисления в расчетной таблице:

Интервальная оценка параметров модели (пример) n Вычислим оценки дисперсии n Построим доверительный интервал: n Вывод: средняя сменная норма добычи на шахтах с мощностью пласта 8 м с надежностью 95% заключается в пределах от 4, 38 до 6, 38 тонны

Интервальная оценка параметров модели (пример) n Найдем оценку дисперсии индивидуального значения: n Построим доверительный интервал: n Вывод: индивидуальная сменная норма добычи на шахтах с мощностью пласта 8 м с надежностью 95% заключается в пределах от 2, 81 до 7, 95 тонны