Линейная множественная модель и её статистический анализ

Линейная множественная модель и её статистический анализ

Классическая нормальная линейная модель множественной регрессии • Вид модели: • Основные предпосылки: 1) ошибка ε – случайный вектор, переменные Х – детерминированные (неслучайные) 2) 3, 4) ошибки не коррелированы 5) ошибка ε – нормально распределенный случайный вектор 6) независимость столбцов объясняющих переменных (невырожденность матрицы)

Классическая нормальная линейная модель множественной регрессии (матричная форма) • Вид уравнения: • Обозначения: - вектор значений зависимой переменной, - матрица значений объясняющей переменной - вектор параметров - вектор возмущений

Оценка параметров модели (по методу наименьших квадратов) • Оценка модели по выборке: - эмпирическая модель • Теорема Гаусса-Маркова: Найденный по методу наименьших квадратов вектор b – наиболее эффективная оценка для β. • Вектор b находят по формуле:

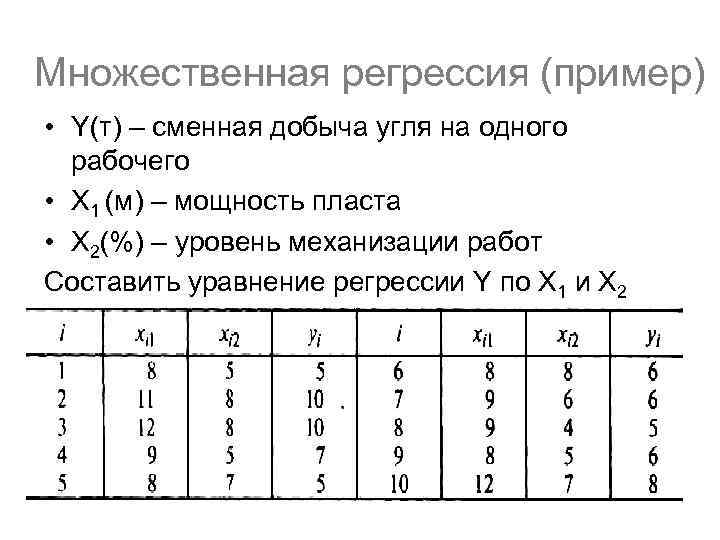Множественная регрессия (пример) • Y(т) – сменная добыча угля на одного рабочего • Х 1 (м) – мощность пласта • Х 2(%) – уровень механизации работ Составить уравнение регрессии Y по X 1 и Х 2

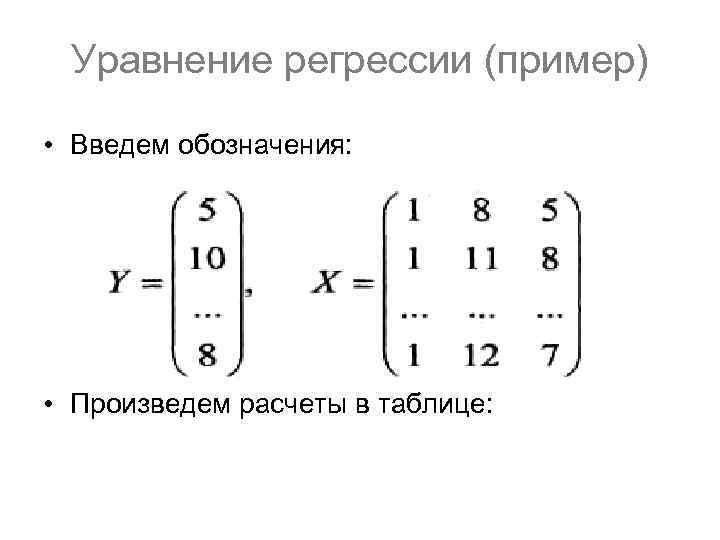Уравнение регрессии (пример) • Введем обозначения: • Произведем расчеты в таблице:

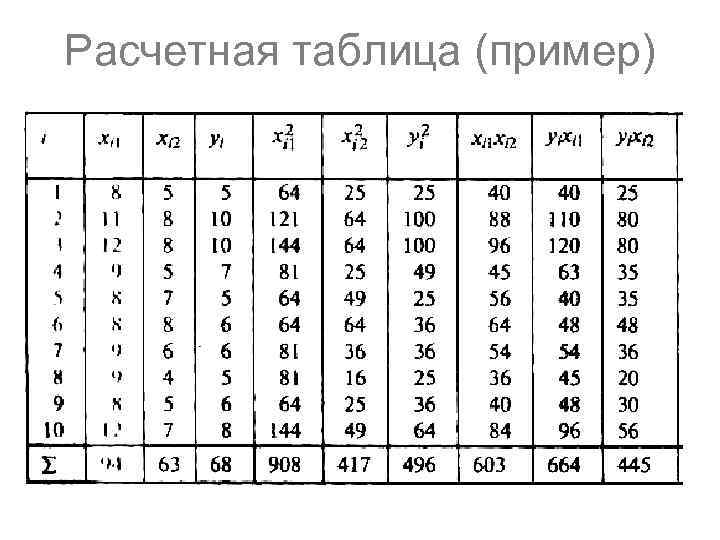Расчетная таблица (пример)

Уравнение регрессии (пример)

Уравнение регрессии (пример)

Анализ множественной модели

I. Оценка влияния факторов на зависимую переменную • Показатели: - стандартизированные коэффициенты регрессии - средние коэффициенты эластичности

Оценка влияния факторов (пример) • Найдем необходимые величины в расчетной таблице: • Рассчитаем стандартизированные коэффициенты: • Найдем коэффициенты эластичности:

II. Оценка параметров множественной регрессии • Доверительный интервал для функции регрессии (среднего значения зависимой переменной)

II. Оценка параметров множественной регрессии • Доверительный интервал для индивидуальных значений зависимой переменной

Оценка параметров регрессии (пример) 1. По уравнению регрессии для • • В таблице вычисляем Результат используем в вычислениях:

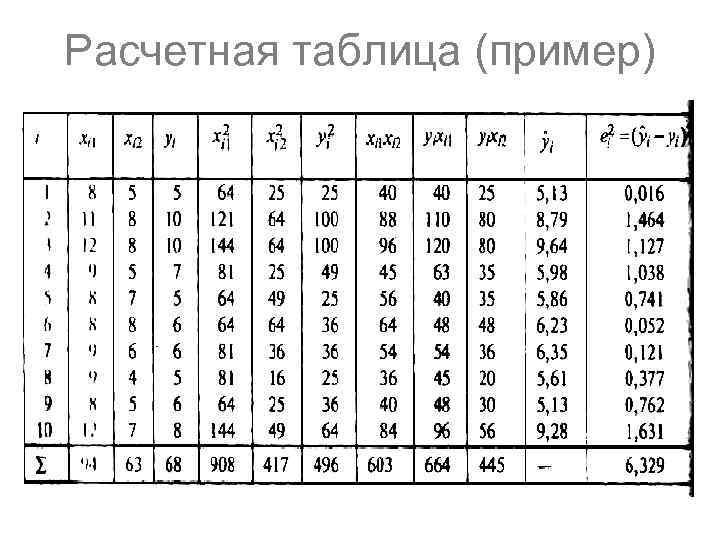Расчетная таблица (пример)

Оценка параметров регрессии (пример) • По таблице Стьюдента • Итак, - доверительный интервал средних значений. 3. Доверительный интервал индивидуальных значений:

III. Оценка качества модели • Точность модели оценивают с помощью среднего коэффициента аппроксимации • Показывает, на сколько процентов в среднем расчетные значения У отклоняются от фактических. • Допустимый предел 8 -10%, максимально возможный 12 -15%

III. Оценка качества модели • Мерой качества уравнения, характеристикой прогностической силы является множественный коэффициент детерминации R 2. • R 2 показывает долю вариации зависимой переменной У, обусловленной изменением объясняющих переменных Х.

III. Оценка качества модели • Значимость уравнения устанавливается посредством F-теста: 1. Вычислить 2. Найти 3. Сравнить Вывод: уравнение значимо на уровне α

Оценка качества (пример) • Вычислим R 2:

Оценка качества (пример) • Значимость уравнения регрессии: • Для α=0, 05 • Fнабл>Fтабл, уравнение значимо на уровне 0, 05. • Для α=0, 01 • Fнабл>Fтабл, уравнение значимо на уровне 0, 01.