Линейная алгебра.ppt
- Количество слайдов: 126



Линейная алгебра Тема 1. Теория определителей. § 1. Определение матрицы. Определители второго порядка, их основные свойства. § 2. Определители третьего порядка и их свойства § 3. Разложение определителя по строке § 4. Определители более высоких порядков Тема 2. Теория матриц. § 5. Системы линейных уравнений § 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными. § 7. Правило Крамера решения линейных систем § 8. Матрицы, основные определения § 9. Действия над матрицами Тема 3. Системы линейных алгебраических уравнений § 10. Обратная матрица § 11. Решение линейных систем с помощью обратной матрицы § 12. Решение матричных уравнений § 13. Ранг матрицы § 14. Теорема о ранге. Совместность линейных систем. § 15. Общее решение однородной линейной системы.

§ 1. Определение матрицы. Определители второго порядка, их основные свойства m d. e m te a ru. u

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Определение. Матрицей называется прямоугольная таблица чисел Обозначения: А – матрица, аij – элемент матрицы, i – номер строки, в которой стоит данный элемент, j – номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Определение. Числа m и n называются размерностями матрицы. Определение. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Определение. Квадратная матрица A называется треугольной, если все ее элементы ниже (выше) главной диагонали равны нулю. ж 2 5 ц 3 з ч A = з 0 1 8 ч з 0 0 1 ч и ш ж 3 0 0 ц з ч B = з 0 1 0 ч. з 1 0 4 ч и ш

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Определение. Операция замены строк столбцами (или наоборот) в матрице называется транспонированием. Так, для квадратной матрицы А транспонированной матрицей будет матрица

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем и обозначается буквами D или .

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Определение. Определителем второго порядка или детерминантом, соответствующим квадратной матрице назовем такое число, что

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Примеры:

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Свойство 1. Определитель не изменяется при транспонировании. d. e m te a Действительно, и, сравнивая, получаем, что m D = D*. ru. u

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Свойство 2. При перестановке двух строк или столбцов определитель меняет свой знак. Действительно, После перестановки столбцов получим Сравнивая, получаем, что D = - D*.

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Свойство 3. Определитель с двумя одинаковыми строками равен нулю. Свойство 4. Определитель, содержащий нулевую строку, равен нулю. Свойство 5. Если все элементы какого-либо столбца (или строки) определителя умножить (или разделить) на одно и то же число m, отличное от нуля, то определитель также умножится (разделится) на это число.

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Свойство 6. Определитель, у которого элементы одной строки (столбца) пропорциональны другой строке (столбцу), равен нулю. Свойство 7. Если каждый элемент какой-либо строки (столбца) можно представить как сумму двух слагаемых, то определитель будет равен сумме двух определителей. У первого из слагаемых определителей элементами соответствующей строки (столбца) будет первое слагаемое, а у другого — второе. Остальные элементы этих определителей будут такие же, как у исходного.

§ 1. Определение матрицы. Определители второго порядка, их основные свойства Свойство 8. Определитель не изменяется, если к элементам какого-либо столбца (строки) прибавить соответствующие элементы другого столбца (строки), предварительно умноженные на какое-либо отличное от нуля число. . Пример.

§ 2. Определители третьего порядка и их свойства Определение 1. Определителем третьего порядка, соответствующего матрице размерности 3× 3, называется число D, равное Для вычисления определителя третьего порядка применяют две вычислительные схемы, позволяющие вычислять определители третьего порядка без особых хлопот. Эти схемы известны, как правило треугольника (или правило звездочки) и правило Саррюса.
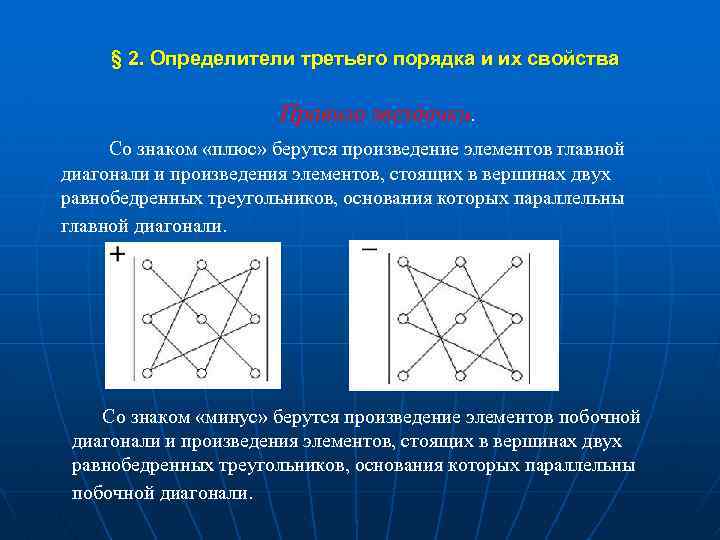
§ 2. Определители третьего порядка и их свойства Правило звездочки. Со знаком «плюс» берутся произведение элементов главной диагонали и произведения элементов, стоящих в вершинах двух равнобедренных треугольников, основания которых параллельны главной диагонали. Со знаком «минус» берутся произведение элементов побочной диагонали и произведения элементов, стоящих в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали.

§ 2. Определители третьего порядка и их свойства Правило Саррюса. По правилу Саррюса, к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в одном направлении, и из нее вычитают сумму произведений элементов в другом направлении (см. схему).

§ 2. Определители третьего порядка и их свойства Пример. Вычислить определитель Решение. по правилу звездочки: по правилу Саррюса:

§ 2. Определители третьего порядка и их свойства Заметим, что все свойства, сформулированные для определителей второго порядка, справедливы для определителей третьего порядка, в чем можно убедиться самостоятельно. На основании этих свойств сформулируем общие свойства для определителей. Свойство 1. Определитель не изменяется при транспонировании:

§ 2. Определители третьего порядка и их свойства Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы. Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т. е.

§ 2. Определители третьего порядка и их свойства Свойство 3. Определитель, имеющий нулевую строку, равен нулю. Свойство 4. Определитель, имеющий две равные строки, равен нулю. Свойство 5. Определитель с пропорциональными строками равен нулю.

§ 2. Определители третьего порядка и их свойства Свойство 6. Перестановка двух строк определителя меняет его знак. Свойство 7.

§ 2. Определители третьего порядка и их свойства Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

§ 2. Определители третьего порядка и их свойства Свойство 8 позволяет значительно упростить вычисление определителя путем сведения его к треугольному виду, если учесть следующую теорему: Теорема. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали. В дальнейшем будем называть такой метод вычисления методом с использованием свойств определителя. Пример.

§ 3. Разложение определителя по строке Определение 1. Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент. Обозначения: выбранный элемент определителя, его минор. Пример.

§ 3. Разложение определителя по строке Определение 2. Алгебраическим дополнением Aij элемента определителя называется его минор, если сумма индексов данного элемента i + j есть число четное, или число, противоположное минору, если i + j нечетно, т. е. Так, в условиях предыдущего примера

§ 3. Разложение определителя по строке Рассмотрим еще один способ вычисления определителей третьего порядка – так называемое разложение по строке или столбцу. Для этого докажем следующую теорему. Теорема 1. Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т. е. где i = 1, 2, 3. Доказательство.

§ 3. Разложение определителя по строке Докажем теорему для первой строки определителя, так как для любой другой строки или столбца можно провести аналогичные рассуждения и получить тот же результат. Найдем алгебраические дополнения к элементам первой строки: Тогда

§ 3. Разложение определителя по строке Пример. Вычислить разложением по первому столбцу определитель Решение. Заметим, что А 31 искать не надо, т. к. a 31=0, поэтому а 31 А 31=0.

§ 3. Разложение определителя по строке Из теоремы 1 вытекает следующее свойство определителей. Свойство 9. Сумма произведений элементов любого столбца (строки) на алгебраические дополнения элементов другого столбца (строки) определителя равна нулю. Доказательство. Проведем доказательство на примере определителя третьего порядка. Возьмем сумму произведений элементов третьей строки на алгебраические дополнения первой строки. Получим

§ 4. Определители более высоких порядков Для квадратных матриц размерности n×n при n>3 можно также записать определитель n-го порядка Свойства определителей 3 -го порядка справедливы и для определителей n-го порядка. На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и, в конечном счете, свести задачу к нахождению определителей 3 -го порядка.

§ 4. Определители более высоких порядков Задача упрощается, если в строке (столбце), по которой разлагается определитель, есть элементы, равные нулю. Тогда алгебраические дополнения этих элементов вычислять не нужно, т. к. соответствующие слагаемые в разложении определителя равны нулю из-за умножения на нулевые элементы. Чем больше нулей, тем легче жить.

§ 4. Определители более высоких порядков Более того, использование свойства 8 и теоремы об определителе треугольной матрицы позволяет свести вычисление определителя квадратной матрицы к вычислению определителя треугольной матрицы (так называемый метод вычисления с использованием свойств определителя). Пример. Вычислим определитель 4 -го порядка Решение.

§ 4. Определители более высоких порядков Чем физик отличается от математика? Задача 1: есть чайник, плита, кружка и пакетик чая. Необходимо заварить чай. Физик решает эту задачу следующим образом: берет чайник, наливает в него воду, ставит чайник на плиту, включает ее и ждет пока закипит вода. После этого он кладет пакетик чая в кружку и наливает туда кипяток. Задача решена. Математик поступает также. Задача 2: есть кипящий чайник, плита, кружка и пакетик чая. Необходимо заварить чай. Физик берет кружку, кладет в нее пакетик чая, наливает кипяток. Математик берет чайник, выливает из него воду и говорит, что задача сводится к предыдущей.

§ 4. Определители более высоких порядков Таким образом,

§ 4. Определители более высоких порядков Пример. Вычислить определитель Решение. Обнулим элементы первого столбца (исключая а 31 ): .

§ 5. Системы линейных уравнений

§ 5. Системы линейных уравнений Определение 1. Линейными операциями над какими-либо объектами называются их сложение и умножение на число. Определение 2. Линейной комбинацией переменных называется результат применения к ним линейных операций, т. е. где αi - числа, xi – переменные. Определение 3. Линейным уравнением называется уравнение вида где ai , b - числа, xi – переменные. Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число. Определение 4. Линейное уравнение называется однородным, если b = 0. В противном случае уравнение называется неоднородным.

§ 5. Системы линейных уравнений Определение 5. Системой линейных уравнений (линейной системой) называется система вида где αij, bi числа, xi неизвестные, n – число неизвестных, m – число уравнений. Определение 6. Решением линейной системы называется набор чисел которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.

§ 5. Системы линейных уравнений Линейная система может иметь единственное решение, бесконечно много решений или не иметь ни одного решения. Примеры. Единственным решением является пара х = 5, у = 3. Решением этой системы будут любые два числа х и у, удовлетворяющие условию у = 3 – х. Например, x = 1, у = 2; x = 0, у = 3 и т. д. Очевидно, что эта система не имеет решений, так как разность двух чисел не может принимать двух различных значений.

§ 5. Системы линейных уравнений Определение 7. Систему уравнений, имеющую хотя бы одно решение, называют совместной; систему, не имеющую решений – несовместной. Определение 8. Если совместная система имеет единственное решение, то она называется определенной; если совместная система имеет по крайней мере два различных решения, то она называется неопределенной. Определение 9. Системы называются эквивалентными, если они имеют одно и то же множество решений.

§ 5. Системы линейных уравнений Укажем элементарные преобразования, которые переводят линейную систему в эквивалентную. • перестановка любых двух уравнений; • умножение обеих частей любого уравнения на любое число, отличное от нуля; • прибавление к обеим частям одного из уравнений соответствующих частей другого, умноженных на любое число.

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Рассмотрим способы нахождения решения системы, в которой число уравнений равно числу неизвестных: Иоганн Карл Фри дрих Га усс 1777 — 1855 великий немецкий математик, астроном и физик

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Суть метода Гаусса: а) из всех уравнений системы кроме первого исключается неизвестное x 1; б) из всех уравнений системы кроме первого и второго исключается неизвестное x 2; в) из всех уравнений системы кроме первого, второго и третьего исключается неизвестное x 3 и т. д.

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Покажем, как реализовать, например, действие а). Пусть а 11≠ 0 (этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на а 11 и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на аi 1 где i – номер очередного уравнения Полученная таким образом новая система будет равносильна исходной в силу того, что проведенные преобразования элементарны.

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду: Из последнего уравнения получившейся системы единственным образом определяется хп , а затем последовательной подстановкой – остальные неизвестные.

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Рассмотрим подробнее все частные случаи приведенных по методу Гаусса систем на примере систем с тремя неизвестными. Случай 1. Система методом Гаусса приведена к следующему виду: В данном случае система имеет единственное решение которое получается последовательным нахождением переменных, начиная с последнего уравнения:

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Случай 2. Система методом Гаусса приведена к следующему виду: В данном случае система, из-за последнего уравнения, несовместна, и, следовательно, не имеет решений.

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Случай 3. Система методом Гаусса приведена к следующему виду: Последнее уравнение системы обратилось в ноль, и система стала неопределенной, т. е. имеет бесчисленное множество решений. Запишем решение системы следующим образом:

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Пример 1. Решить методом Гаусса систему Решение. Отсюда z = 3, y = 2, x = 1 – единственное решение системы. ПРОВЕРКА !!!!!!!

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Пример 2. Решить методом Гаусса систему Решение. В системе осталось два уравнения: т. е. система неопределена. Ее решение можно записать в виде: z ПРОВЕРКА !!!!!!! = k, у =7 -k, х = -2,

§ 6. Метод Гаусса решения линейных систем n уравнений с n неизвестными Пример 3. Решить методом Гаусса систему Решение. Последнее равенство является неверным при любых значениях неизвестных, следовательно, система не имеет решения, т. е. несовместна.

§ 7. Правило Крамера решения линейных систем Рассмотрим способы нахождения решения системы трех уравнений первой степени с тремя неизвестными : Габриэ ль Кра мер 1704— 1752 швейцарский математик, один из создателей линейной алгебры.

§ 7. Правило Крамера решения линейных систем Определение 1. Определитель составленный из коэффициентов при неизвестных данной системы, называется главным определителем этой системы. Введем обозначения для определителей, получаемых из главного определителя системы путем замены соответствующего столбца неизвестных на столбец свободных членов:

§ 7. Правило Крамера решения линейных систем Покажем, что имеет место соотношение Произведем следующее преобразование: Сложим все три полученных уравнения: Коэффициенты при y и z в силу свойства 3. 1. определителей равны нулю, а коэффициент при х на основании теоремы 3. 1 равен Таким образом, и

§ 7. Правило Крамера решения линейных систем Таким образом, имеют место соотношения Рассмотрим следующие возможные случаи. Тогда решение системы находим как так называемые формулы Крамера. Тогда система не имеет решения (система несовместна). Система либо не имеет решения, либо имеет бесконечное множество решений.

§ 7. Правило Крамера решения линейных систем Пример 1. Решить по правилу Крамера систему Решение. Вычислим определители Поскольку Δ=8, то данная система имеет единственное решение, которое найдем по формулам Крамера: т. е. (2, 0, – 1) искомое решение системы. ПРОВЕРКА !!!!!!!

§ 7. Правило Крамера решения линейных систем Пример 2. Решить по правилу Крамера систему Решение. Вычислим определители Поскольку Δ=Δх=0, а Δy=2≠ 0 , то данная система несовместна.

§ 7. Правило Крамера решения линейных систем Пример 3. Решить по правилу Крамера систему Решение. Вычислим определители Данная система не имеет решений, так как первое и третье уравнения противоречивы. Если умножить первое уравнение на 3 и вычесть из полученного уравнение третье, то придем к ложному равенству 0 = 3.

§ 7. Правило Крамера решения линейных систем Пример 4. Решить по правилу Крамера систему Решение. Вычислим определители Данная система равносильна системе двух уравнений относительно трех неизвестных Т. о. система неопределена. Ее решение можно записать в виде: ПРОВЕРКА !!!!!!!

§ 8. Матрицы, основные определения m d. e m te a ru. u

§ 8. Матрицы, основные определения Определение 1. Матрицей называется прямоугольная таблица чисел Обозначения: А – матрица, аij – элемент матрицы, i – номер строки, в которой стоит данный элемент, j – номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

§ 8. Матрицы, основные определения Определение 2. Числа m и n называются размерностями матрицы. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.

§ 8. Матрицы, основные определения Определение 3. Квадратная матрица A называется треугольной, если все ее элементы ниже (выше) главной диагонали равны нулю.

§ 8. Матрицы, основные определения Определение 4. Операция замены строк столбцами (или наоборот) в матрице называется транспонированием. Так, для квадратной матрицы А транспонированной матрицей будет матрица

§ 8. Матрицы, основные определения Определение 5. Нулевая матрица – матрица, все элементы которой равны нулю: Определение 6. Диагональная матрица n-го порядка это квадратная матрица n-го порядка, в которой отличны от нуля только элементы, стоящие на главной диагонали:

§ 8. Матрицы, основные определения Определение 7. Квадратная матрица А называется симметричной относительно главной диагонали, если aij = a ji. Определение 8. Матрицу, состоящую из элементов одного столбца, называют столбцовой матрицей. Матрицу, состоящую из элементов одной строки, называют строчной:

§ 8. Матрицы, основные определения Определение 9. Единичной матрицей называют диагональную матрицу с единицами на главной диагонали: Определение 10. Квадратная матрица называется невырожденной, если определитель ее не равен нулю. Если определитель равен нулю, то матрица называется вырожденной.

§ 8. Матрицы, основные определения Определение 11. Две матрицы А и В считаются равными, если они имеют одинаковое количество столбцов и строк и их элементы aij и bij равны между собой. Определение 12. Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, если порядок матрицы A равен m×n, то порядок согласованной с ней матрицы B должен быть равен n×k (отметим, что квадратные матрицы одного порядка всегда согласованы). Пример согласованных матриц: 2× 3 3× 3

§ 8. Матрицы, основные определения Определение 13. Матрица A (m×n) называется ступенчатой, если в каждой ее строке есть элемент, в столбце которого все элементы ниже являются нулями, а в последней строке есть хотя бы один ненулевой элемент. Упомянутые в определении ненулевые элементы называют ведущими. Примером ступенчатой матрицы служит верхняя треугольная матрица любой размерности. Ступенчатыми являются также матрицы Теорема. Любую ненулевую матрицу можно путем элементарных преобразований свести к эквивалентной ей ступенчатой матрице.

§ 9. Действия над матрицами 1. Сложение матриц Определение 1. Суммой двух матриц A = (aij) и B = (bij) с одинаковым количеством строк и столбцов называется матрица C = (cij), у которой элементом cij является сумма соответствующих элементов aij и bij матриц А и В. Пример. СВОЙСТВА СЛОЖЕНИЯ: • А + В = В + А (переместительный закон). • (А + В) + С = А + (В + С) (сочетательный закон). • Если О – нулевая матрица, то А + О = О + А = А.

§ 9. Действия над матрицами 2. Умножение матрицы на число Определение 2. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число. СВОЙСТВА УМНОЖЕНИЯ МАТРИЦЫ НА ЧИСЛО: (km)A = k(m. A). k(A + B) = k. A + k. B. (k + m)A = k. A + m. A. Определение 3. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т. е. С = А + ( 1)В.

§ 9. Действия над матрицами 3. Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго, т. е. матрицы должны быть согласованными. Определение 9. 4. Произведением матрицы А размерности m p и матрицы В размерности p n называется матрица С размерности m n, каждый элемент которой сij определяется формулой:
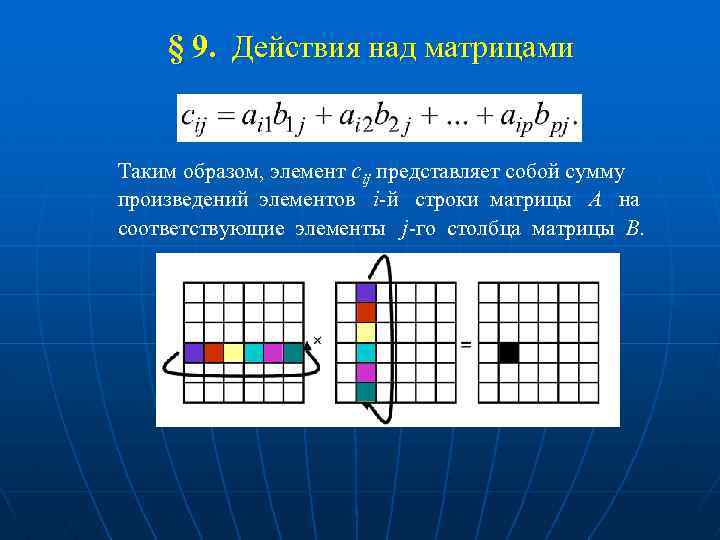
§ 9. Действия над матрицами Таким образом, элемент сij представляет собой сумму произведений элементов i-й cтроки матрицы А на соответствующие элементы j-го столбца матрицы В.

§ 9. Действия над матрицами Пример 1. Найти А∙B и B∙A. Решение. 1) Найдем произведение А∙B. Матрицы А[2× 3] и B[3× 3] (именно в таком порядке) согласованы, и результирующая матрица С будет иметь размерность [2× 3]. 2) Произведение В∙А не существует ввиду несогласованности матриц B[3× 3] и А[2× 3](именно в таком порядке).

§ 9. Действия над матрицами Пример 2. Найти А∙B и B∙A. Решение. Матрицы А[2× 2] и B[2× 2] ( в любом порядке) согласованы, и результирующая матрица С будет иметь размерность [2× 2]. Пример 2 показывает, что произведение матриц не подчиняется переместительному закону. Однако произведение подчиняется сочетательному А(ВС) = (АВ)С и распределительному (А + В)С = =АС + ВС законам. Определение 5. Если произведение матриц подчиняется переместительному закону, т. е. АВ = ВА, то такие матрицы называют перестановочными.

§ 9. Действия над матрицами Теорема 1. Определитель произведения двух квадратных матриц равен произведению их определителей. Доказательство проведем для матриц второго порядка. При умножении на единичную матрицу АЕ = А и ЕА = А, т. е. при умножении матриц, единичная матрица играет роль единицы:

§ 10. Обратная матрица Определение 1. Если А – квадратная матрица, то обратной для нее является матрица А-1, удовлетворяющая условию А А-1 = Е, либо А-1 А = Е. Теорема 1. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной. Доказательство. Необходимость: Так как то по теореме об определителе произведения двух матриц

§ 10. Обратная матрица Достаточность: Зададим матрицу А-1 в следующем виде: Составим матрицу и докажем, что

§ 10. Обратная матрица Найдем несколько элементов матрицы С. по теореме § 3. по свойству 9 § 3. по теореме § 3. Таким образом, любой элемент матрицы С, не лежащий на главной диагонали, равен 0, а элементы, стоящие на главной диагонали, равны 1, т. е. Теорема доказана.

§ 10. Обратная матрица Сформулируем алгоритм вычисления обратной матрицы А-1: 1) Находим ΔА. Если ΔА≠ 0, то А-1 существует. 2) Составляем союзную матрицу 3) Транспонируем союзную матрицу 4) Находим обратную матрицу

§ 10. Обратная матрица Пример. Найти обратную матрицу для Решение. Определитель матрицы Так как матрица А невырожденная, следовательно, существует ей обратная матрица. Вычисляем алгебраические дополнения:

§ 10. Обратная матрица Союзная матрица Обратная матрица Легко удостовериться, что

§ 11. Решение линейных систем с помощью обратной матрицы Рассмотрим линейную систему и введем следующие обозначения: матрица системы, столбец неизвестных, столбец свободных членов.

§ 11. Решение линейных систем с помощью обратной матрицы Тогда исходную систему можно записать в виде матричного уравнения: АХ = В. (*) Пусть матрица А – невырожденная, тогда существует обратная к ней матрица А-1. Умножим обе части равенства (*) слева на А-1. Получим Но тогда откуда Итак, решением матричного уравнения (*) является произведение матрицы, обратной к А, на столбец свободных членов исходной системы.

§ 11. Решение линейных систем с помощью обратной матрицы Пример. Решить матричным методом систему уравнений: Решение. В матричной форме эта система запишется в виде A X = B , где Решение уравнения в матричном виде X=А— 1 B. Ранее в § 10 было найдено, что Тогда ПРОВЕРКА !!!!

§ 12. Решение матричных уравнений Рассмотрим решение матричных уравнений следующего вида: Здесь А – заданная квадратная матрица порядка n , В, С – заданные прямоугольные матрицы размеров X, Y – искомые матрицы размеров и и Основная идея решения матричных уравнений заключается в умножении матрицы А на обратную матрицу А-1 (слева или справа) с последующим использованием соотношения

§ 12. Решение матричных уравнений Умножим слева обе части уравнения на матрицу А-1: или Пример. Решить матричное уравнение Решение. ПРОВЕРКА !!!!

§ 12. Решение матричных уравнений Умножим справа обе части уравнения на матрицу А-1: или Пример. Решить матричное уравнение Решение. Ранее в § 10 было найдено, что ПРОВЕРКА !!!! или

§ 13. Ранг матрицы Рассмотрим матрицу, содержащую m строк и n столбцов: Выделим в этой матрице произвольные K строк и K столбцов. Элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу порядка K. Определение 1. Минором K-го порядка матрицы А называется определитель квадратной матрицы, получающийся из данной матрицы выделением произвольных K строк и K столбцов.

§ 13. Ранг матрицы Пример. Для заданной матрицы записать миноры 1 -го, 2 -го, 3 -го порядков: Решение. Минорами 1 -го порядка являются сами элементы матрицы. Минорами 2 -го порядка можно выделить определители Минорами 3 -го порядка можно выделить определители

§ 13. Ранг матрицы Определение 2. Угловым минором K-го порядка матрицы А называется минор матрицы, получающийся выделением первых K строк и K столбцов. Так, для рассмотренной выше матрицы Определение 3. Рангом матрицы называется наивысший порядок ее ненулевого минора. Обозначается r (A), Rg(А). Замечание 1. Очевидно, что значение ранга матрицы не может превышать меньшей из ее размерностей. Замечание 2. Если ранг матрицы равен r, то все миноры (r+1) порядка равны нулю.

§ 13. Ранг матрицы Пример. Определить ранг матрицы Решение. Единственным минором 4 -го порядка матрицы является определитель (как определитель с нулевой строкой). Т. к. один из миноров 3 -го порядка матрицы, например, угловой минор то ранг данной матрицы равен 3, r(A) = 3.

§ 13. Ранг матрицы Определение 4. Матрицы, имеющие одинаковые ранги, называются эквивалентными. Для определения ранга матриц большой размерности необходимо преобразовать матрицу к так называемому ступенчатому виду при помощи эквивалентных преобразований. К ним относятся: • транспонирование; • умножение строки на ненулевое число; • перестановка строк; • прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число; • вычеркивание нулевой строки.

§ 13. Ранг матрицы Пример. Определить ранг матрицы Решение. Теоретически ранг этой матрицы может принимать значения от 1 до 4. Угловой минор последней матрицы следовательно, r(A) = 2.

§ 14. Теорема о ранге. Совместность линейных систем Определение 1. Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы. Определение 2. Выражение вида - некоторые числа, а где - строки (столбцы) матрицы А, называется линейной комбинацией строк (столбцов) матрицы А. Если числа равны нулю одновременно то такая линейная комбинация называется тривиальной. Если хотя бы одно число то такая линейная комбинация называется нетривиальной.

§ 14. Теорема о ранге. Совместность линейных систем Определение 3. Строки (столбцы) матрицы называются линейно зависимыми, если существует их нетривиальная линейная комбинация, такая, что Определение 4. Строки (столбцы) матрицы называются линейно независимыми, если из условия следует тривиальность линейной комбинации

§ 14. Теорема о ранге. Совместность линейных систем Теорема 1. Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Доказательство (для строк). Если бы базисные строки были линейно зависимыми, то и базисный минор содержал бы нулевую строку, получаемую при помощи эквивалентных преобразований, что противоречит условию, что базисный минор не равен нулю.

§ 14. Теорема о ранге. Совместность линейных систем Теорема 2. Любая строка (столбец) матрицы является линейной комбинацией строк (столбцов) базисного минора. Доказательство (для строк). 1. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0. 2. Докажем это свойство для k-ой строки, не входящей в базисный минор. Добавим к базисному минору эту строку и любой j-ый столбец. Затем разложим полученный определитель, равный нулю (так как его порядок больше ранга матрицы) по j-му столбцу: Разделим на т. к. он является базисным минором. Имеем: Следовательно, выбранная строка является линейной комбинацией базисных строк.

§ 14. Теорема о ранге. Совместность линейных систем Рассмотрим систему линейных алгебраических уравнений Назовем расширенной матрицей этой системы матрицу вида а матрицей системы – матрицу А из коэффициентов при неизвестных:

§ 14. Теорема о ранге. Совместность линейных систем Теорема 3. (теорема Кронекера-Капелли). Система m уравнений с n неизвестными совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. Доказательство. Необходимость: пусть система совместна и ее решение. Тогда т. е. столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, т. е.

§ 14. Теорема о ранге. Совместность линейных систем Достаточность: если то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации то эти числа будут решением системы, т. е. эта система совместна. Теорема доказана.

§ 14. Теорема о ранге. Совместность линейных систем КРОНЕКЕР, ЛЕОПОЛЬД (1823 -1891), немецкий математик, известный своими работами по высшей алгебре и теории линейных уравнений Капелли Альфредо (1855 - 1910) Итальянский математик. В Берлинском университете слушал лекции Вейерштрасса и Кронекера. Его лекции по алгебре (1895) при жизни автора выдержали четыре издания.

§ 14. Теорема о ранге. Совместность линейных систем Исторический комментарий. Понятие ранга матрицы и результат, известный в литературе как «теорема Кронекера–Капелли» , были открыты несколькими независимыми исследователями. Первое доказательство этой теоремы принадлежит Ч. Л. Додсону, оно было напечатано им в 1867 г. Дод(ж)сон Чарльз Лютвидж (Dod(g)son Charles Lutwidge, 1832 -1898). Один из самых знаменитых математиков мира работал магистром (Master of House) Тринити-колледжа в Оксфорде, и имел сан дьякона. Д. был болезненно застенчив, глух на одно ухо, заикался. Был крайне педантичен: записывал в особую тетрадь содержание всех отправляемых и получаемых им писем — последнее зарегистрировано номером 98721.

§ 14. Теорема о ранге. Совместность линейных систем Его трудами зачитывались (и зачитываются до сих пор) все — от школьника до королевы Виктории. Самые популярные его книги подписаны псевдонимом, полученным двойным переводом личных имен: Лью ис Кэ рролл англ. Lewis Carroll, настоящее имя Чарльз Лю твидж До джсон, Charles Lutwidge Dodgson; 1832— 1898 английский писатель, математик, логик, философ и фотограф.

§ 14. Теорема о ранге. Совместность линейных систем Замечание. Договоримся в качестве базисных выбирать угловые миноры (естественно, в тех случаях, когда это возможно). Определение 5. Неизвестные, коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные – свободными неизвестными.

§ 14. Теорема о ранге. Совместность линейных систем Из теоремы следует, что для системы m уравнений с n неизвестными возможны следующие случаи: 1. r(A) < r(В). В этом случае система несовместна, т. е. решений не имеет. 2. r(A) = r(В) = r. В этом случае система совместна, т. е. имеет хотя бы одно решение. При этом: - если r = n (n число неизвестных), то система имеет единственное решение; - если r < n , то система имеет бесконечное число решений, которые находятся следующим образом: • в матрице А выделяется любой базисный минор r-го порядка, • выделяется подсистема, состоящая из уравнений, коэффициенты при неизвестных которых являются базисными строками или входят в базисный минор, • полученная подсистема решается по формулам Крамера при произвольных значениях (n r) неизвестных, коэффициенты которых не входят в минор.

§ 14. Теорема о ранге. Совместность линейных систем Пример. Исследовать систему Решение. Приведем расширенную матрицу к ступенчатому виду:

§ 14. Теорема о ранге. Совместность линейных систем Очевидно, что r(A) = 3; r(В) = 4. Система решений не имеет.

§ 14. Теорема о ранге. Совместность линейных систем Пример. Исследовать систему Решение. d. e m te a Составим матрицы m Приведем расширенную матрицу к ступенчатому виду: ru. u

§ 14. Теорема о ранге. Совместность линейных систем d. e m te a ru. u m Очевидно, что r(A) = r(В) = 3 = n, т. е. равно количеству неизвестных. Следовательно, система имеет единственное решение. Находим его.

§ 14. Теорема о ранге. Совместность линейных систем За базисный возьмем угловой минор Решаем систему из трех уравнений: Методом Гаусса находим х3 = 3. И далее находим х1 = 1; х2 = 2. Ответ: х1 = 1, х2 = 2, х3 = 3.

§ 14. Теорема о ранге. Совместность линейных систем Пример. Исследовать систему Решение. Приведем расширенную матрицу к ступенчатому виду: Очевидно, что r(А) = r(В) = 2, т. е. r < n - имеется множество решений. За базисный возьмем угловой минор За базисные неизвестные выберем х1 и х2, и так коэффициенты при х1 и х2 являются элементами базисного минора, то х3 и х4 будут свободными неизвестными.

§ 14. Теорема о ранге. Совместность линейных систем отсюда Для того чтобы найти решение системы, дадим произвольные значения свободным неизвестным, например x 3 = k; x 4 = l: По методу Гаусса находим решение общее решение системы как Частное решение можно получить, придав произвольные значения параметрам k, l. Например, для k = 0, l = 0 получаем следующее частное решение:

§ 15. Общее решение однородной линейной системы Рассмотрим однородную линейную систему m уравнений с n неизвестными Имеет место теорема Кронекера – Капелли. Расширенная матрица В получается из матрицы А системы добавлением столбца, состоящего из одних нулей, поэтому ранг матрицы А всегда равен рангу расширенной матрицы В, т. е. однородная система всегда совместная.

§ 15. Общее решение однородной линейной системы Возможны два случая: 1. r(A)=n. Тогда однородная система имеет единственное нулевое решение называемое тривиальным. Действительно, все определители, получаемые из главного определителя системы путем замены j-го столбца на столбец свободных членов, будут равны нулю, и по формулам Крамера имеем

§ 15. Общее решение однородной линейной системы 2. r(A)<n. Предположим, что в базисный минор входят коэффициенты первых r уравнений. Тогда оставшиеся (m – r) уравнений являются линейными комбинациями, то есть следствиями предыдущих. Поэтому в системе можно оставить только первые r уравнений: Эта система будет иметь единственное решение относительно неизвестных Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо. выражающее их через остальные неизвестные. Таким образом, однородная система при r < n является неопределенной.

§ 15. Общее решение однородной линейной системы Подводя итог, заметим, что необходимым и достаточным условием нетривиальных решений однородной системы является условие r(A)<n, где А матрица коэффициентов при неизвестных, n число неизвестных. Замечание. Для систем n уравнений с n неизвестными наличие нетривиального решения возможно лишь в случае, когда определитель системы равен нулю.

§ 15. Общее решение однородной линейной системы Перепишем исходную однородную систему в матричном виде: Пусть матрица-столбец есть одно из решений этой системы. Решения системы линейных однородных уравнений обладают следующими свойствами. 1. Матрица-столбец 2. Если матрицы-столбцы тоже есть решение этой системы. и решения однородной системы, то их линейная комбинация также является ее решением.

§ 15. Общее решение однородной линейной системы Из сформулированных выше свойств следует, что всякая линейная комбинация решений однородной системы также является решением этой системы. Представляет интерес найти такие линейно независимые решения однородной системы, через которые линейно выражались бы все остальные ее решения. Определение. Система линейно независимых решений называется фундаментальной, если каждое решение однородной системы является линейной комбинацией решений

§ 15. Общее решение однородной линейной системы Теорема 1. Если для однородной системы r(A)<n, то всякая фундаментальная система решений системы будет состоять из n – r решений. Теорема 2. Если для однородной системы r(A)<n, то фундаментальную систему решения Х можно получить, взяв следующие n – r независимые матрицы – столбцы: Тогда, согласно теореме, любое решение однородной системы имеет вид:

§ 15. Общее решение однородной линейной системы Пример. Решить систему Очевидно, что r(A) = 2. За базисный возьмем угловой минор Тогда Пусть тогда общее решение системы имеет вид

§ 15. Общее решение однородной линейной системы Найдем фундаментальную систему решения. Пусть Тогда т. е. Получена фундаментальная система решений: Общее решение системы можно записать в виде:
m d. e m te a ru. u
Линейная алгебра.ppt