Линейная алгебра ТЕМА 1 Матрицы и определители

Линейная алгебра ТЕМА № 1 Матрицы и определители

Определители n – ого порядка Определителем n – ого порядка квадратной матрицы называется число: Методы вычисления определителей n – ого порядка рассмотрим на примере вычисления определителей третьего порядка.

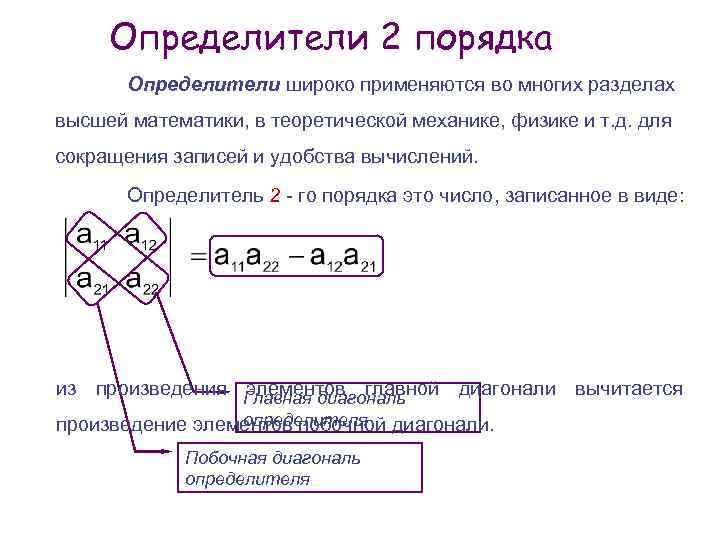
Определители 2 порядка Определители широко применяются во многих разделах высшей математики, в теоретической механике, физике и т. д. для сокращения записей и удобства вычислений. Определитель 2 - го порядка это число, записанное в виде: из произведения Главная диагональ элементов главной диагонали вычитается определителя произведение элементов побочной диагонали. Побочная диагональ определителя

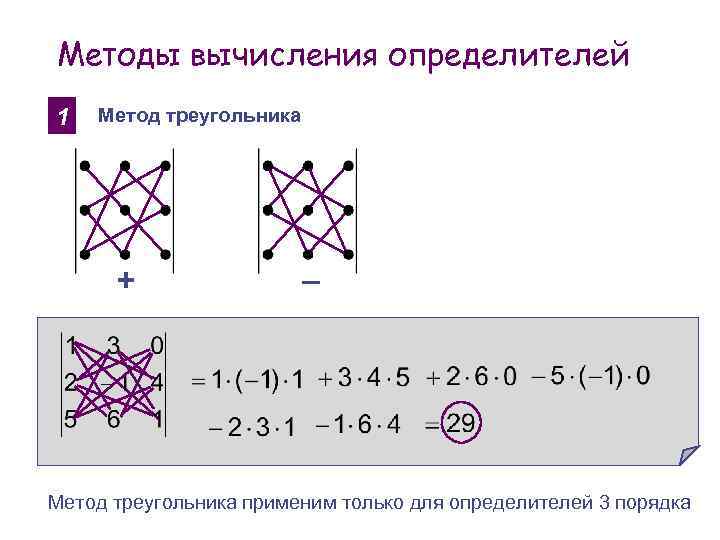
Методы вычисления определителей 1 Метод треугольника + _ Метод треугольника применим только для определителей 3 порядка

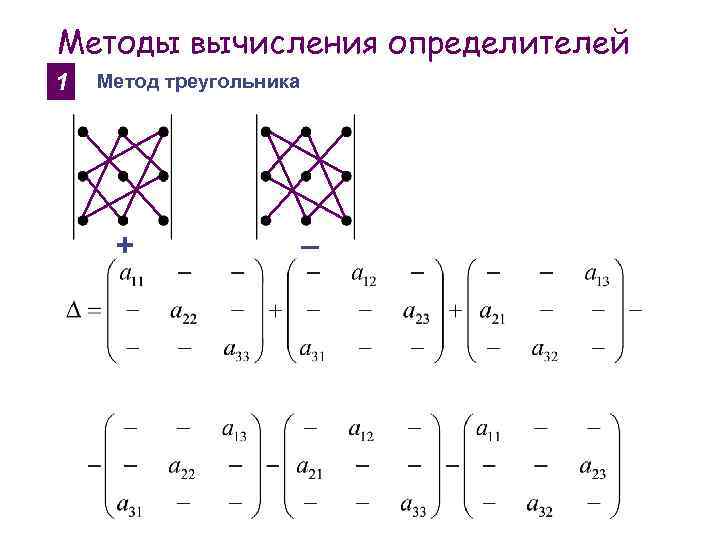
Методы вычисления определителей 1 Метод треугольника + _

Методы вычисления определителей 2 Метод разложения определителя по элементам строки (столбца) Определитель второго порядка, который получается из определителя 3 - го порядка путем вычеркивания i - й строки и j - го столбца, т. е. строки и столбца, на пересечении которых стоит элемент ai j называется минором элемента и обозначается Mi j Алгебраическим дополнением элемента ai j называется

Методы вычисления определителей Величина определителя равна сумме произведений элементов какой – либо строки (столбца) определителя на их алгебраические дополнения: Разложение определителя по элементам i – ой строки Разложение определителя по элементам j – ого столбца

Методы вычисления определителей Разложение определителя по 2 -й строке

Методы вычисления определителей

Пример вычисления определителя путем разложения по элементам первой строки: Наиболее выгодным является разложение определителя по элементам того ряда, в котором все элементы, кроме одного, равны нулю. Например, данный определитель наиболее выгодно разложить по элементам 2 -й строки Если строк или столбцов с нулями нет, то их можно получить, используя элементарные определителя. преобразования, не меняющие величины

Методы вычисления определителей 3 Использование свойств определителя Свойства определителя: Величина определителя: равна нулю, если элементы какого - либо столбца или строки равны нулю: равна нулю, если соответствующие элементы двух строк (столбцов) равны

Методы вычисления определителей меняет знак, если поменять местами строки (столбцы): увеличивается в k раз, если элементы какого - либо столбца (строки) увеличить в k раз: Пример:

Методы вычисления определителей Определитель не меняется при замене строк соответствующими столбцами: Определитель равен нулю, если все элементы какого-либо ряда равны нулю:

Методы вычисления определителей не меняется, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель Если определитель имеет так называемый треугольный вид, то он вычисляется как произведение чисел, стоящих на главной диагонали:

Методы вычисления определителей Определитель равен соответствующие пропорциональны: нулю, элементы если есть которых два ряда, равны или

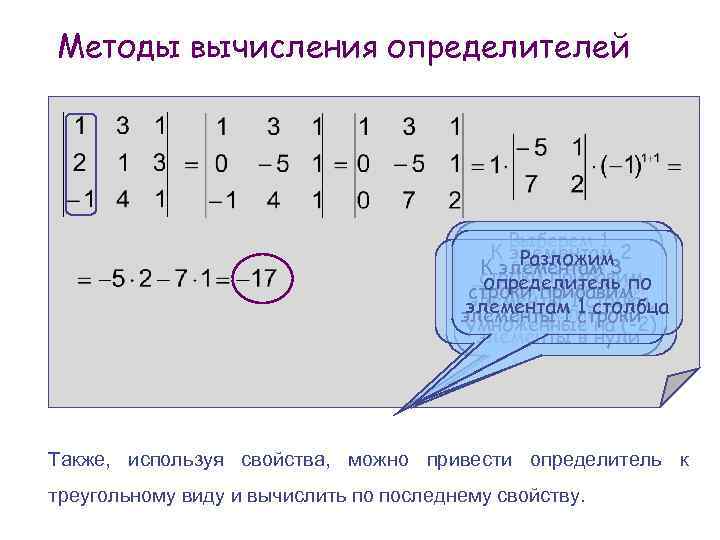
Методы вычисления определителей Выберем 1 К элементам 2 Разложим столбец и К элементам 3 строки прибавим определитель по превратим второй строки прибавим элементы столбца элементам 11 строки, и третий элементы 1 строки умноженные на (-2) элементы в нули Также, используя свойства, можно привести определитель к треугольному виду и вычислить по последнему свойству.

Согласно свойству определителей: Величина определителя не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы другого ряда, предварительно умноженные на число.

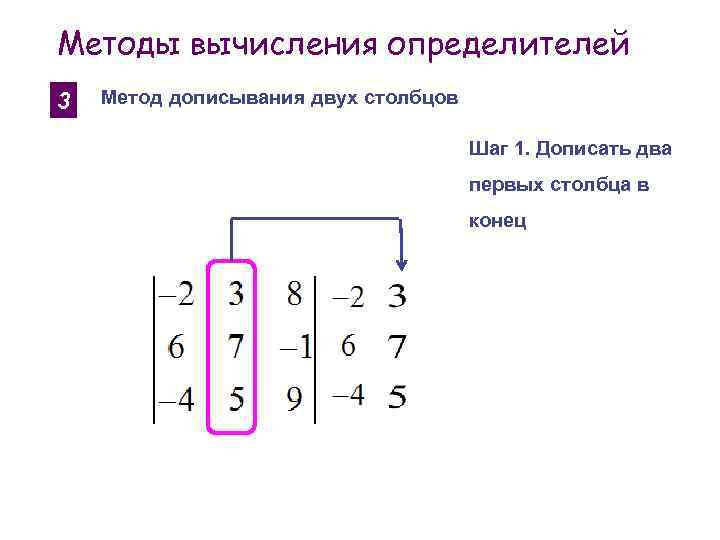
Методы вычисления определителей 3 Метод дописывания двух столбцов Шаг 1. Дописать два первых столбца в конец

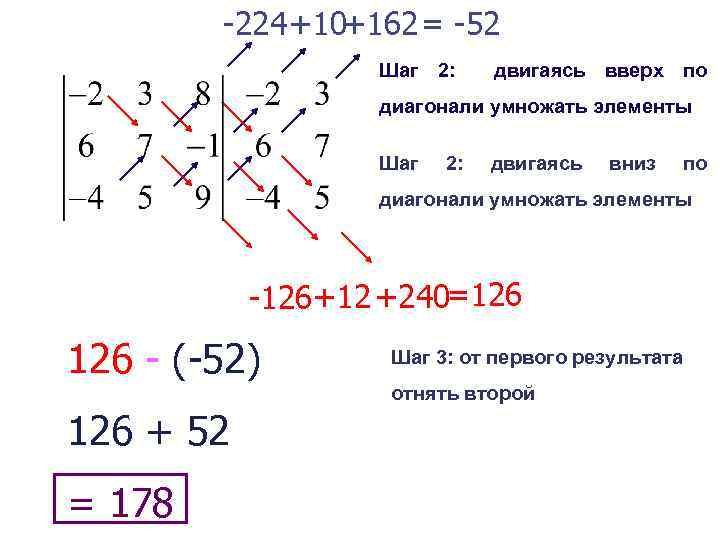
-224+10+162= -52 Шаг 2: двигаясь вверх по диагонали умножать элементы Шаг 2: двигаясь вниз по диагонали умножать элементы -126+12 +240=126 - (-52) Шаг 3: от первого результата отнять второй 126 + 52 = 178