Линейная алгебра Литература 1 Б Ш

Линейная алгебра • • Литература 1. Б. Ш. Гулиян, Р. Я. Хамидуллин Математика. Базовый курс, М. ООО «Маркет ДС Корпорейшн, 2008.

Введение • Линейная алгебра - это теория линейных алгебраических структур (линейных пространств, линейных отображений и т. д. ). Результаты линейной алгебры, теории матриц необходимы во многих областях. Основное внимание мы будем уделять решению систем линейных уравнений со многими неизвестными.

Решение системы линейных уравнений со многими неизвестными !

• Линейная алгебра проявляет единство двух основных подходов математики- абстрактности и приложимости. Для менеджеров и экономистов это путь к линейному программированию.

• Линейность представляет весьма общее понятие. Все линейные модели, процессы и явления обладают свойствами аддитивности и однородности. Аддитивность в математическом смысле означает следующее: если действие х приводит к эффекту , а действие у приводит к эффекту , то совместное действие х+у приводит к совместному эффекту + .

• Однородность означает, что если х приводит к эффекту , то х+х приводит к эффекту + , т. е. в общем случае kx приводит к эффекту k . аддитивность линейность однородность

• С математической точки зрения линейные модели имеют определенные преимущества, т. к. линейные задачи всегда решаются (в том смысле, что не может сложиться ситуация, когда не бывает известно имеет ли решение задача). • Еще в 4 в. до н. э. Тамарид решал систему уравнений. Баше де Мезирак [1587 -1638] предложил решение в целых числах системы с двумя уравнениями. • Почти все линейные модели сводятся к системам алгебраических линейных уравнений или неравенств.

Модуль вектора • Как уже упоминалось, очень важной характеристикой вектора является его длина (модуль). Модуль вектора по определению равен (обобщенная теорема Пифагора) • • • Числа х1, х2, х3 называются компонентами или координатами вектора.

Операции над векторами • Мы также будем записывать вектор кратко буквой со стрелкой. На множеств векторов вводится операция сложения и умножения на скаляр (т. е. векторное пространство), которые определяются так: • Если хотя бы одна операция не определена, то это не векторы. Определена также геометрическая схема сложения.

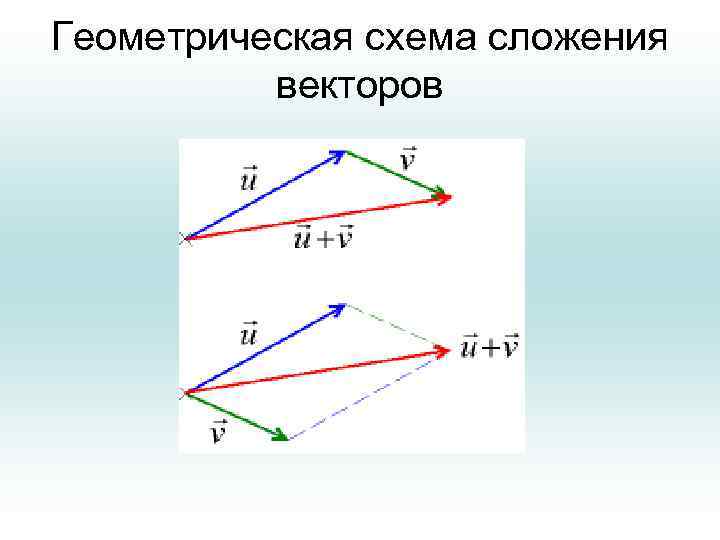
Геометрическая схема сложения векторов

Векторы • В пространстве имеется так называемый естественный или стандартный базис (о базисе ниже) из трех (единичных) векторов • В этом случае вектор

Векторы представим в виде • Эти две записи (правая и левая) можно рассматривать как эквивалентные. Говорят, что вектор х разложим по векторам еi. Разложение вектора по базису единственно. Концепция разложения векторов на составляющие весьма полезна.

Линейная зависимость векторов Множество векторов {an} называется линейно зависимым, если существуют коэффициенты {kn} не все равные нулю, что линейная комбинация равна нулю k 1 a 1 + k 2 a 2 + k 3 a 3=0. Другими словами, если линейная комбинация равна нулю, но хотя бы один коэффициент отличен от нуля, то вектора линейно зависимы.

Линейная зависимость векторов Если векторы линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Подмножество векторов, не являющееся линейно зависимым, называется линейно независимым. Любое подмножество линейно независимого множества также линейно независимо.

Пример линейно зависимых векторов Пример. Вектора на плоскости (-1; 4) и (2; -8) линейно зависимы, т. к. их линейная( одна из многих) комбинация равна нулю: -2 (-1; 4) - (2; -8)=0.

n-мерное векторное пространство. Базис Совокупность n линейно независимых векторов n-мерного векторного пространства V, порождающих это пространство, называется его базисом. Существует много различных базисов. Однако все они обладают следующим свойством: любой элемент из нашего пространства V можно разложить по базису единственным способом.

• Единичным вектором является вектор, у которого длина равна единице (например, у вектора лишь одна компонента равна единице, а остальные равны нулю). • Вектор можно записывать в виде столбца

Скалярное произведение векторов • Векторы можно перемножать. Допустим, что у нас имеется два вектора • и обозначает угол между этими векторами. Тогда число, полученное по формуле

Скалярное произведение векторов • называют скалярным произведением векторов и обозначают также a b или a, b . Скалярное произведение векторов является скалярной величиной. Оно может быть вычислено простым умножением модуля вектора a на проекцию вектора b на a или перемножением соответствующих компонент векторов и сложением результатов (суммирование попарных произведений):

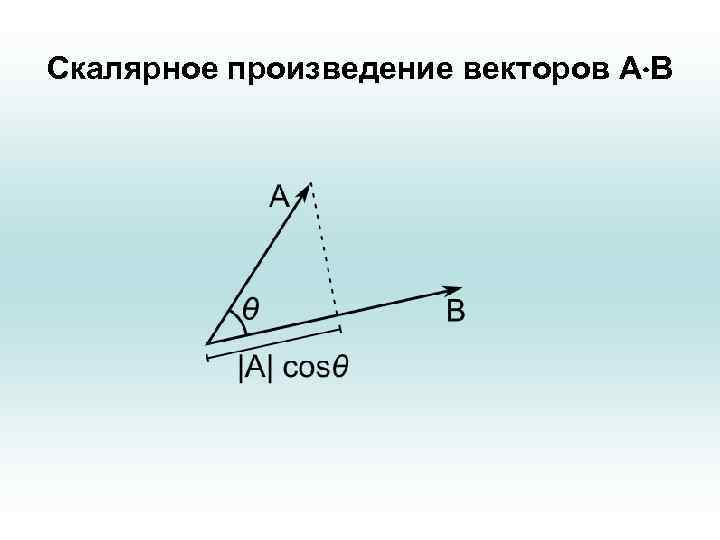
Скалярное произведение векторов А В

Скалярное произведение векторов • Векторы a и b называются ортогональными, если их скалярное произведение равно нулю a b = 0. Скалярное произведение линейно. • Скалярное произведение позволяет нам ОПРЕДЕЛИТЬ норму (длину) вектора: • Косинус угла между векторами равен:

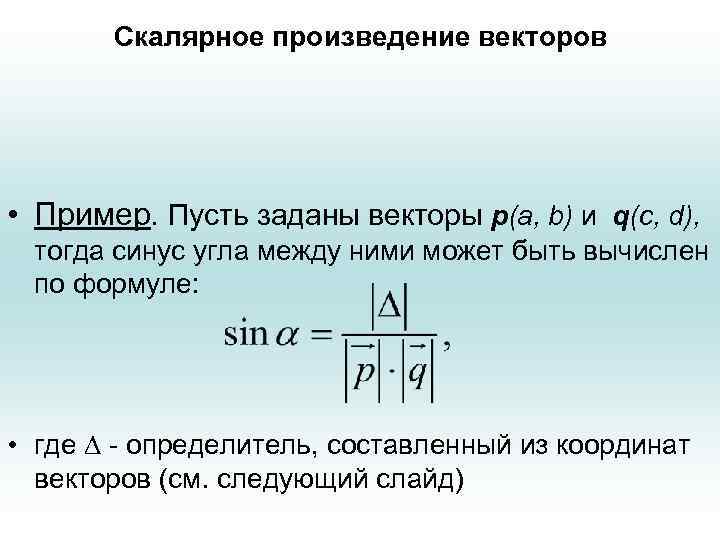
Скалярное произведение векторов • Пример. Пусть заданы векторы р(a, b) и q(c, d), тогда синус угла между ними может быть вычислен по формуле: • где - определитель, составленный из координат векторов (см. следующий слайд)

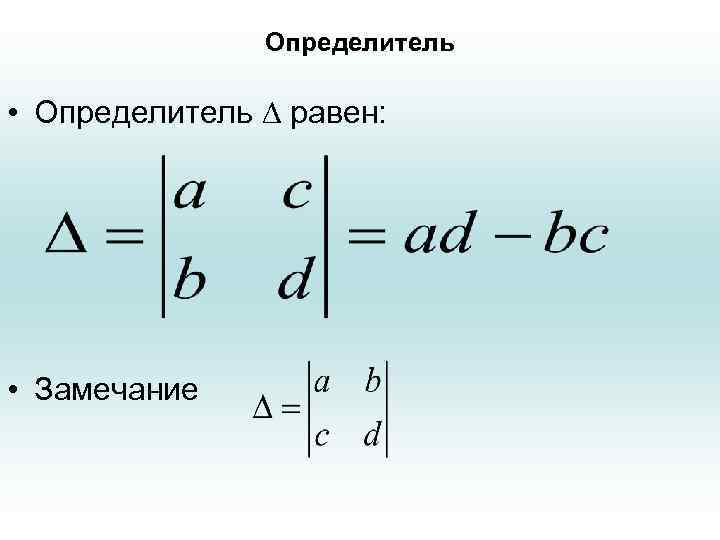
Определитель • Определитель равен: • Замечание

Площадь параллелограмма • Утверждение. Пусть ABCD произвольный параллелограмм, заданный векторами р(a, b) и q(c, d). Тогда площадь S параллелограмма равна . • В самом деле: Замечание. Площадь треугольника равна 1/2

Равенство нулю определителя Определитель треугольной матрицы равен произведению диагональных элементов.

Определитель треугольной матрицы • Например. Рассмотрим пример нахождения определителя. Мы можем к любой строке прибавить строку. Воспользуемся этим для преобразования определителя к

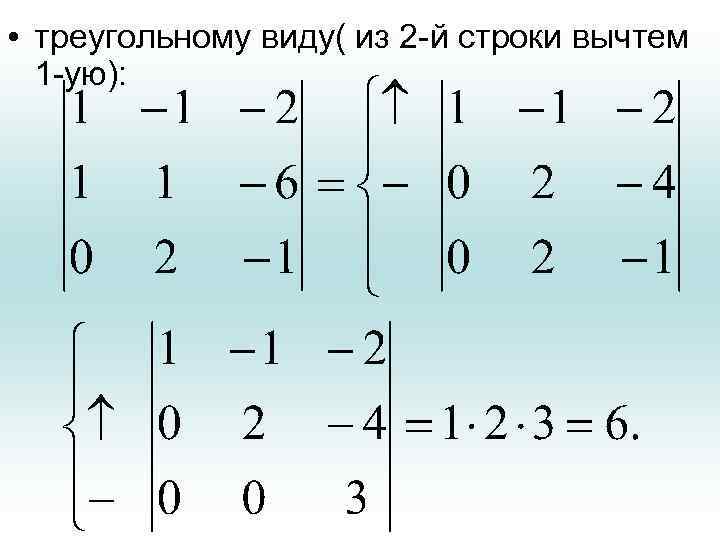
• треугольному виду( из 2 -й строки вычтем 1 -ую):

• Значение этого определителя не надо искать, т. к. его величина равна нулю(!). Третий столбец пропорционален первому.

ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦ • Матрица – это определенным образом представленное множество чисел. Для удобства вычислений и обращения с ними, матрицы записываются в виде таблицы. С математической точки зрения матрицы ведут себя как вектора (линейные объекты) и они образуют векторное пространство. Чтобы рассмотреть этот объект более подробно нужно обратиться к системе линейных алгебраических уравнений. Но сначала приведем основные положения.

ОСНОВНЫЕ ПОНЯТИЯ • Матрица состоит из элементов – чисел. • Нулевой матрицей называется матрица, у которой все элементы – нули. Квадратная матрица размера n называется единичной, если все её элементы, стоящие на главной диагонали, равны единице, а все остальные – нули. Единичная матрица, как правило, обозначается буквой E или I:

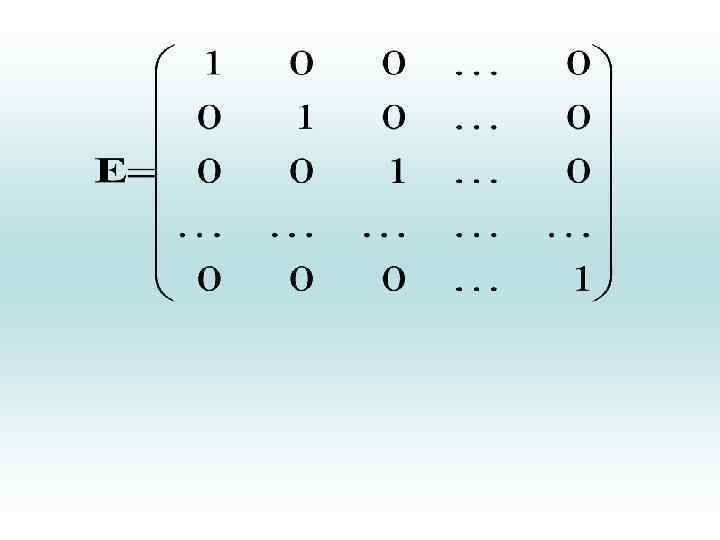
ЭЛЕМЕНТЫ ТЕОРИИ МАТРИЦ • Основные понятия. • Рассмотрим систему m линейных алгебраических уравнений с n неизвестными:

• Решением системы называется упорядоченный набор из n чисел, обращающий каждое уравнение системы в тождество. • Система, имеющая решение, называется совместной. • Если система имеет только одно решение, то она называется определенной. • Если система не имеет решений, то она называется несовместной.

• Если число уравнений системы совпадает с числом неизвестных, то система называется квадратной. • Преобразование, переводящее систему в новую систему, эквивалентную исходной, называется элементарным. • К элементарным преобразованиям относятся следующие преобразования: • перестановка местами двух уравнений системы, • перестановка местами (переобозначение)

двух неизвестных с учетом их коэффициентов (симметрично у всех уравнений), • умножение/деление обеих частей какого -либо уравнения системы на отличное от нуля число, • замена уравнения системы на сумму или разность этого уравнения с любым другим уравнением системы (прибавление к уравнению линейной комбинации других уравнений).

• Если применить рассмотренные элементарные преобразования к матрице, то важнейшая ее характеристика - ранг не будет меняться. Сама матрица при этом изменит вид (подобно системе уравнений), но суть ее не изменится.

ВАЖНО ! ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ

? ЧТО ТАКОЕ МАТРИЦА ?

Далее мы будем основываться на системе (1) и рассмотрим прямоугольную таблицу, состоящую из p строк и q столбцов, которую мы назовем матрицей системы размера p q:

Можно сказать что, матрица – это прямоугольная таблица множества чисел, которые занумерованы определенным порядком (матрицу часто изображают жирным шрифтом)

• Числа aij (i = 1, 2, , m; j =1, 2, , n) называются элементами матрицы. Первый индекс фиксирует номер строки, а второй – номер столбца, в которых стоит данный элемент. Например, элемент а 12 стоит в первой строке, во втором столбце. Множество всех p q матриц обозначим М p, q. Если число столбцов матрицы равно числу строк, то матрица называется квадратной (Мn). Элементы aii образуют главную диагональ матрицы, идущую из левого верхнего угла в правый нижний (например, а 11, а 22…).

• Представленная матрица (2) называется матрицей коэффициентов системы линейных уравнений (1), а матрица (3)– расширенной матрицей для исходной системы уравнений. • Для того, чтобы получить расширенную матрицу, мы к матрице коэффициентов системы прибавляем (приписываем справа) столбец свободных элементов нашей системы (т. е. правые части). Число столбцов при этом увеличивается на единицу, а число строк остается тем же самым.

• На множестве матриц вводится понятие равенства. Две матрицы одинаковой размерности p q называются равными, если в них все элементы с одинаковыми индексами равны. Приведем далее пример верхней треугольной матрицы

• На множестве согласованных (одинаковых) матриц вводится операция сложения, которая обозначается символом «плюс» + и также, по аналогии с векторами, вводится операция умножения матрицы на число ( «точка» ), т. е. задается векторное пространство (Мp, q). Рассмотрим умножение на число. • Пусть A = (aij) – некоторая матрица и – произвольный скаляр, т. е. действительное число.

• Под произведением A понимается матрица ( aij), то есть при умножении матрицы A на число все элементы матрицы A, умножаются на это число. • Сложение. Пусть A и B – матрицы одинаковой размерности: • A = (aij), B = (bij). Под суммой A + B понимается матрица C = (cij) той же размерности, каждый элемент которой определяется покомпонентным сложением по формуле: cij = aij + bij.

• Сложение матриц

• Операция сложения матриц коммутативна и ассоциативна (как для векторов). • На множестве матриц вводится операция умножения одной матрицы на другую. Умножению матриц отвечает композиции линейных отображений. Эта операция чем-то напоминает скалярное умножение векторов (х1 у1 + х2 у2 +х3 у3 ). • Нейтральным элементом при умножении является единичная матрица. • Необходимо отметить следующее: • произведение определяется только для

• тех матриц, для которых выполняется следующее условие: • матрицу A можно умножить на матрицу B ( C = A B), если число столбцов матрицы A равно числу строк матрицы B. • Каждый элемент получившейся матрицы C определяется по формуле:

• т. е. элемент cij матрицы C равен сумме произведений элементов i-ой строки первой матрицы- сомножителя на соответствующие элементы j-го столбца второй матрицы-сомножителя (скалярное произведение строки и столбца). • Из сказанного следует, что если можно найти произведение матриц AB, то произведение BA, вообще говоря, может не существовать( т. е умножение матриц не коммутативно). Но умножение матриц ассоциативно (АВ)С=А(ВС). Заметим, что умножение векторов – коммутативно.

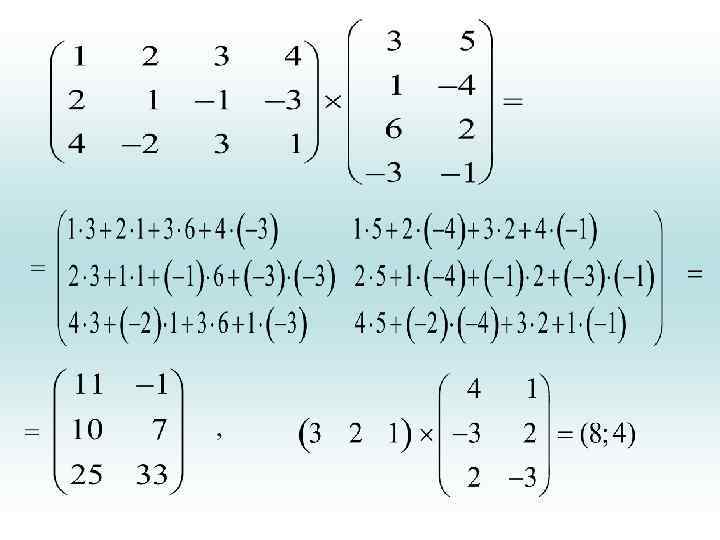
Умножение матриц С=АВ

• Структура произведения =

x 11 x 12 x 13 y 11 y y 31 21 = х11 у11+x 12 y 21+ x 13 y 31= некоторое число

• Если произведения AB и BA одновременно определены, то, вообще говоря, эти произведения могут быть не равны. Это означает, что умножение матриц не коммутативно. Например,

• Мы получили в результате две неравные матрицы. • Если операция произведения матриц выполнима, то выполняется условие дистрибутивности: • (А+В)С=АС+ВС • Общие правила алгебраических действий для матриц: • 1) A + B = B + A;

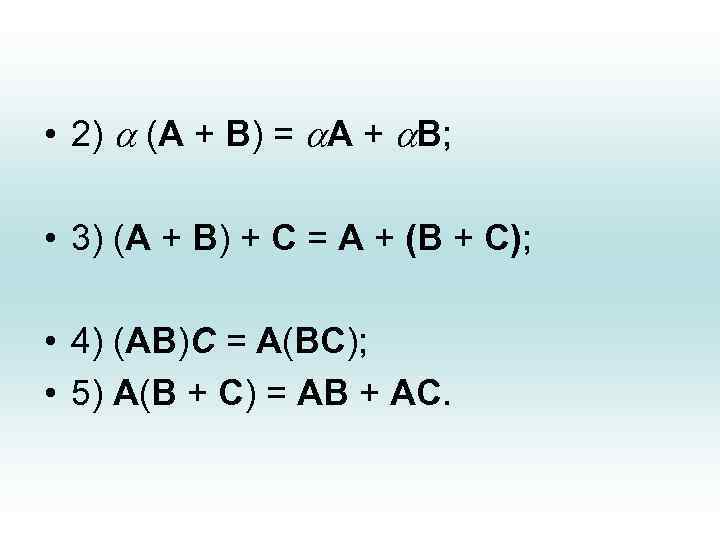
• 2) (A + B) = A + B; • 3) (A + B) + C = A + (B + C); • 4) (AB)C = A(BC); • 5) A(B + C) = AB + AC.

Метод Гаусса решения систем линейных уравнений

Метод Гаусса решения систем линейных уравнений • Метод Гаусса – классический способ решения системы линейных алгебраических уравнений путем последовательного исключения неизвестных и преобразования системы уравнений к ступенчатому (треугольному) виду, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Метод Гаусса решения систем линейных уравнений • Рассмотрим для примера систему двух линейных уравнений с двумя неизвестными, которая имеет вид: • • • где a, b, c, d, g, f – заданные числа; x, y – неизвестные. Числа a, b, c, d – коэффициенты при неизвестных; f, g – свободные члены.

Метод Гаусса решения систем линейных уравнений • Решение этой системы уравнений может быть найдено основными методами подстановки и сложения или же Крамера. • 1. Метод подстановки. • Из одного уравнения выражаем неизвестное, например x, через коэффициенты

Метод подстановки • • • и другое неизвестное - y (предполагаем а≠ 0): x = ( f – by ) / a Подставляем во второе уравнение вместо x : c·( f – by ) / a + dy = g. Находим у и т. д. • 2. Сложение или вычитание. • Этот метод можно проиллюстрировать так.

Метод сложения • Рассмотрим пример. Из одного уравнения вычитаем/складываем другое (это элементарное преобразование), например

Метод Гаусса решения систем линейных уравнений • Идея состоит в исключении переменных. • С точки зрения линейной алгебры этот метод соответствует разложению матрицы коэффициентов в произведение A=NU нижней треугольной N и верхней треугольной матрицы U. • С точки зрения вычислительной математики число арифметических операций при этом пропорционально n 3/3.

Метод Гаусса решения систем линейных уравнений • При решении систем чаще всего число уравнений совпадает с числом неизвестных (например, линейная модель экономики В. Леонтьева или статистические регрессивные модели). В этих случаях удается найти единственное решение задачи. Если число неизвестных больше числа уравнений, например, в задачах линейного программирования, то может существовать бесконечное число решений. Может встретиться система, где число уравнений больше числа неизвестных. Однако может оказаться, что не все эти уравнения

Метод Гаусса решения систем линейных уравнений являются независимыми, а некоторые могут представлять линейную комбинацию других. • В этом случае желательно найти достаточное количество независимых уравнений, чтобы получить решение. • На основе рассмотренного примера при решении произвольных систем возникает желание найти процедуру, например, процедуру последовательного исключения неизвестных и нахождения величин x 1, x 2, …, xn, которые удовлетворяют всем нашим уравнениям. Рассмотрим пример.

• Метод Гаусса решения систем линейных уравнений • Предположим, что нам надо решить систему линейных уравнений, например:

метод • 1. Устанавливается строка, с помощью которой будем производить исключение и находим ведущий элемент (стрелка); • 2. Проводим с помощью элементарных преобразований исключение переменной х1 из всех уравнений (кроме первого); • 3. Аналогично исключаем х2, х3 , … хn-1 , пока не останется одно уравнение; • 4. Система решается снизу вверх путем подстановки найденных решений в соответствующие уравнения.

• В первом уравнении ведущий или разрешающий коэффициент(со стрелочкой) равен двум (не равен нулю). Мы используем первое уравнение для исключения х1. Делим это уравнение на два и три раза отнимаем его из второго уравнения, получаем:

• Первое уравнение у нас остается без изменения. Для дальнейшего исключения х1 просто вычитаем модифицированное первое уравнение из третьего и получаем:

• Используя второе уравнение из новой системы, исключаем х2 в третьем уравнении. Для этого мы можем второе уравнение умножить на пять и вычесть из третьего

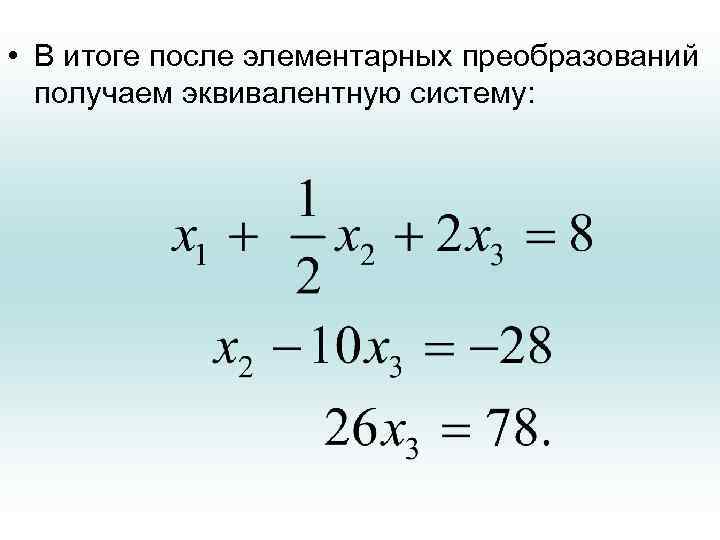
• В итоге после элементарных преобразований получаем эквивалентную систему:

• Из третьего уравнения находим х3 =3. Подставляя это значение в первые два уравнения, находим остальные неизвестные •

• Окончательно находим решение системы х1 =1, х2 =2, х3 =3. • Модифицированный метод (Гаусса. Жордана) предполагает, что первый (и второй) шаг являются таким же как в методе Гаусса и мы получаем систему (5). Далее, используя второе уравнение получаем х2 и результат подставляем и в первое и в третье уравнения. Об этом см. далее. Если в результате преобразований все коэффициенты при неизвестных в какой-нибудь строке окажутся равными

• нулю, а правая часть не будет равна нулю, то данная система несовместна. • Метод Жордана-Гаусса • Решить систему уравнений:

• Запишем матрицу и приведем ее к разрешенному виду за пять шагов (ведущий элемент отмечаем штрихом). Из первой и третьей строк вычитаем вторую:

Из третьей вычитаем первую:

К первой прибавляем третью (6 раз)

Из третьей вычитаем первую:

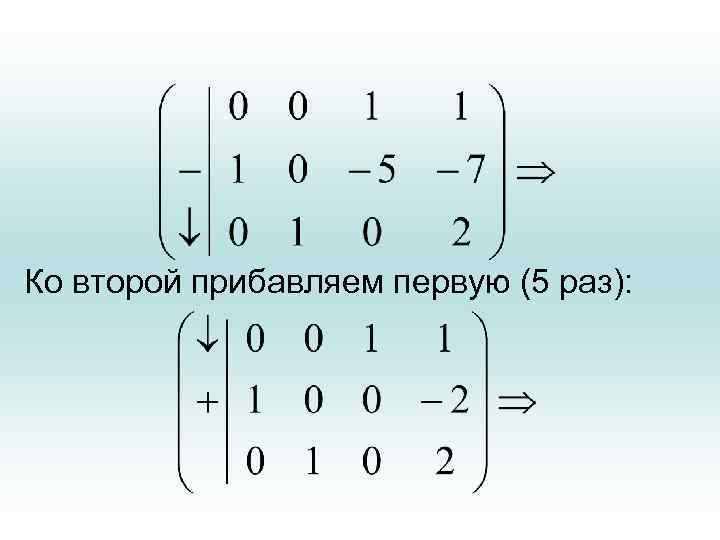
Ко второй прибавляем первую (5 раз):

• В результате исходная система принимает следующий вид: • В итоге имеем решение: х1 =-2; х2 =2; х3 =1.

• Метод Гаусса решения систем линейных уравнений • Рассмотрим квадратную систему линейных уравнений, например:

• Для того, чтобы избавиться от х1 мы должны определиться с коэффициентом a 11 (ведущий элемент) и убедиться, что он отличен от нуля. Если это не так, то нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x 1 не равен нулю. • 1) поскольку в нашем случае a 11 0, первое уравнение оставим без изменений;

• 2) наша задача исключить x 1 из второго и т. д. уравнений; исключим x 1 во втором уравнении системы: для этого вычтем из второго уравнения системы первое уравнение, умноженное на 4; • 3) аналогично исключим x 1 в третьем уравнении системы: для этого вычтем из третьего уравнения системы первое уравнение, умноженное на 3; • 4) исключим x 1 в четвертом уравнении системы: для этого вычтем из четвертого уравнения системы первое уравнение, умноженное на 5. Переменные можно не рассматривать.

Продолжим. Преобразуем полученную матрицу следующим образом: • 1) первые две строки оставим без изменения, поскольку элемент a 22 не равен нулю (=10);

• 2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей; мы можем так поступать. • 3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой. • В результате получится матрица, соответствующая системе, у которой неизвестная x 1 исключена из всех уравнений, кроме первого, а неизвестная x 2 — из всех уравнений кроме первого и второго:

Теперь исключим неизвестную x 3 из четвертого уравнения. Для этого полученную матрицу преобразуем так: • 1) первые три строки оставим без изменения, так как a 33 0; • 2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой:

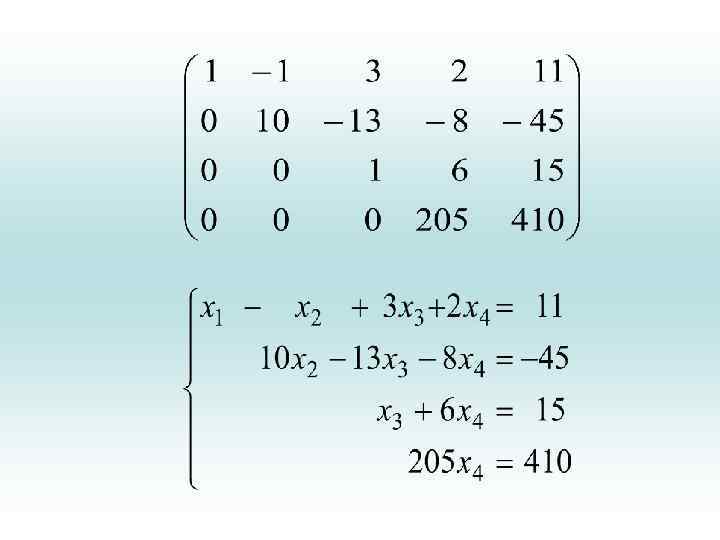
• Очевидно, мы получили треугольную систему. • Отсюда находим : x 4 = 2. Подставив это значение в третье уравнение, получим x 3 = 3. Теперь из второго уравнения следует, что x 2 = 1, а из первого, что x 1 = – 1. Очевидно, что полученное решение единственно (возможна проверка).

• То есть наша матрица представляет собой в общем случае ступенчатую матрицу, которую получили преобразованием (Гаусса). Но может быть это случайно? На самом деле любая матрица посредством серии элементарных преобразований может быть приведена к ступенчатой.

• Транспонирование матрицы. • При транспонировании матрицы строки и столбцы меняются местами. Операция транспонирования обозначается звездочкой или индексом Т.

ОБРАТНАЯ МАТРИЦА

ОБРАТНАЯ МАТРИЦА • Обратная матрица вводится по аналогии с алгебраическим соотношением а а -1=1. • Пусть A – квадратная матрица. Обратной матрицей к матрице A называется такая матрица A– 1, для которой справедливы равенства: А A– 1 = A– 1 A = E. • Таким образом, произведение матрицы на обратную равно единичной матрице.

• Заметим, что не всякая квадратная матрица имеет обратную матрицу. • Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной (т. е. определитель не равен нулю или все строки – линейно независимы). Для того, чтобы найти обратную матрицу к матрице второго порядка 2 х2:

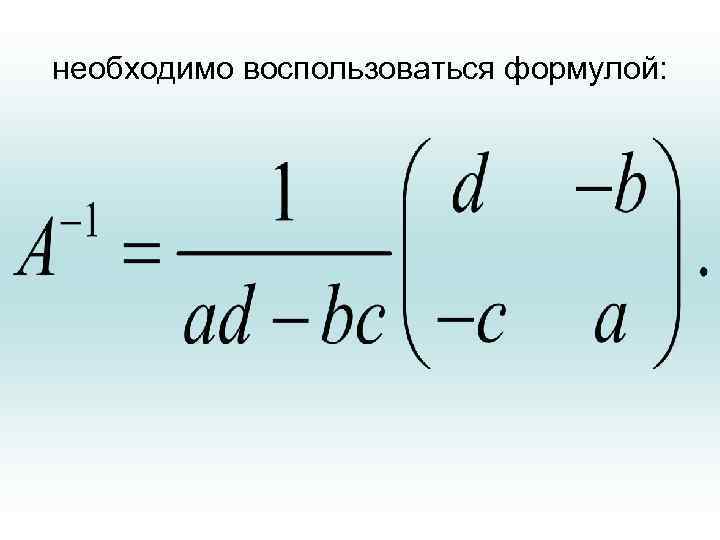
необходимо воспользоваться формулой:

• По этой формуле, если разность ad-bc не равна нулю (т. е. матрица А не вырождена) обратная матрица получается из исходной заменой местами чисел a и d относительно боковой диагонали, при одновременном изменении знака у b и c на противоположный. Вновь полученная матрица умножается на коэффициент (ad-bc)-1. • Например:

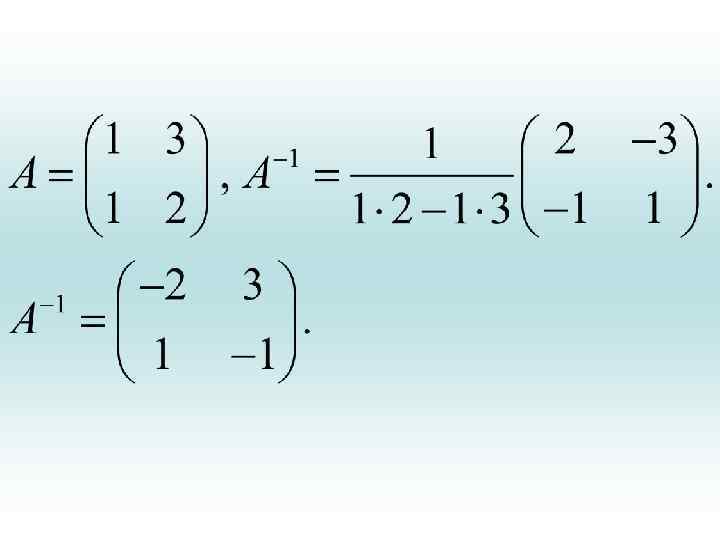
Свойства обратной матрицы • Е-1 =Е; • (А-1) -1 =А. • Для получения обратной матрицы достаточно к строкам единичной матрицы применить те преобразования, которые приводят матрицу А к единичной (метод Жордана-Гаусса).

ОПРЕДЕЛИТЕЛЬ

ТЕОРИЯ ОПРЕДЕЛИТЕЛЕЙ • Основные понятия. • Часто в математике желательно охарактеризовать объект, определяемый многими параметрами, с помощью одной величины. Пример такого рода – определитель. Определитель является инвариантом. •

Определение детерминанта det • Квадратной матрице А (порядка n) ставится в соответствие число, называемое определителем или детерминантом (det), вычисляемое на основе значений ее элементов. Определитель равен алгебраической сумме всевозможных произведений его элементов, по одному из каждой строки и каждого столбца. Слагаемые называются членами определителя.

Определение детерминанта det • Каждый член определителя равен произведению n элементов матрицы А. Число всех членов определителя n -го порядка равно n!.

Свойства определителя • Определитель не меняется при транспонировании матрицы. • Определитель равен нулю тогда и только тогда, когда строки (столбцы) матрицы линейно зависимы. Такая матрица называется вырожденной. • Если любую строку матрицы умножить на число, то и определитель матрицы умножится на это число.

Свойства определителя • Определитель меняет знак, если две строки поменять местами. • !!! Определитель не меняется, если к какой-либо строке матрицы прибавить любую линейную комбинацию остальных строк. • Если элементы строки матрицы представлены в виде суммы aij= bij+cij, то определитель равен сумме двух определителей, у которых все строки,

кроме i–ой такие же, а i–я строка в одном из них содержит элемент bij, а в другом - cij. Определитель треугольной матрицы равен произведению диагональных элементов. Теорема. Определитель произведения квадратных матриц равен произведению определителей матрицсомножителей.

Свойства определителя обратной матрицы det(AВ)=det(A) det(В) -1 )=1/det (A) det(A

МЕТОД КРАМЕРА

• Рассмотрим теперь систему трех линейных уравнений с тремя неизвестными • Эту систему решаем с помощью определителей. Для этого нам нужно найти определитель третьего порядка.

• Определителем произвольной квадратной матрицы третьего порядка • называется сумма шести слагаемых, каждое из которых представляет собой произведение трех элементов матрицы, выбираемых

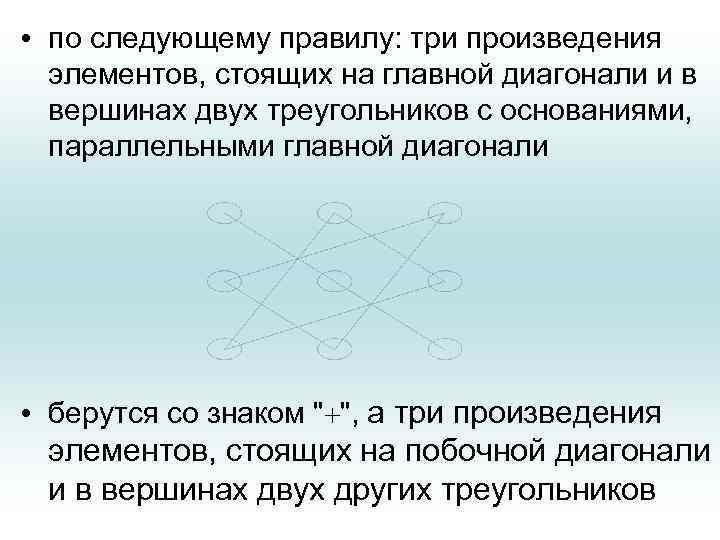
• по следующему правилу: три произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников с основаниями, параллельными главной диагонали • берутся со знаком " ", а три произведения элементов, стоящих на побочной диагонали и в вершинах двух других треугольников

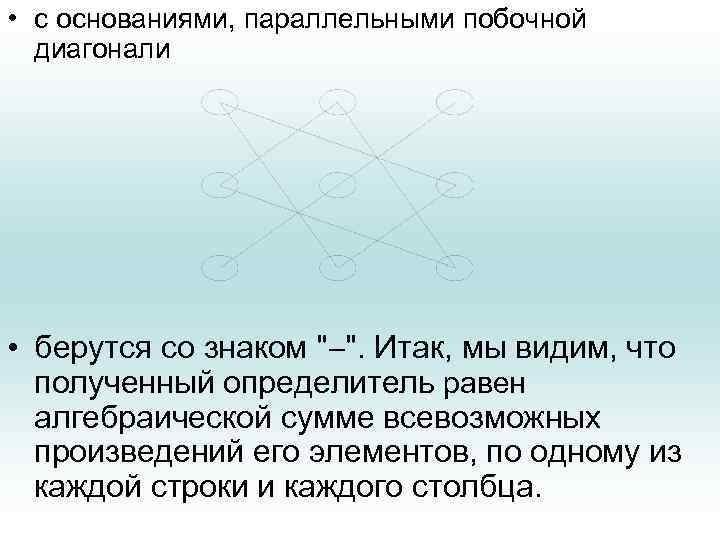
• с основаниями, параллельными побочной диагонали • берутся со знаком " ". Итак, мы видим, что полученный определитель равен алгебраической сумме всевозможных произведений его элементов, по одному из каждой строки и каждого столбца.

Нахождение определителя матрицы А третьего порядка

• Определитель третьего порядка обозначается в вертикальных отрезках:

• Вернемся к решению нашей системы (6). Например методом уравнивания коэффициентов, по аналогии с предыдущим получим: • x 1 = 1; x 2 = 2; x 3 = 3, (7) где «дельта» равны

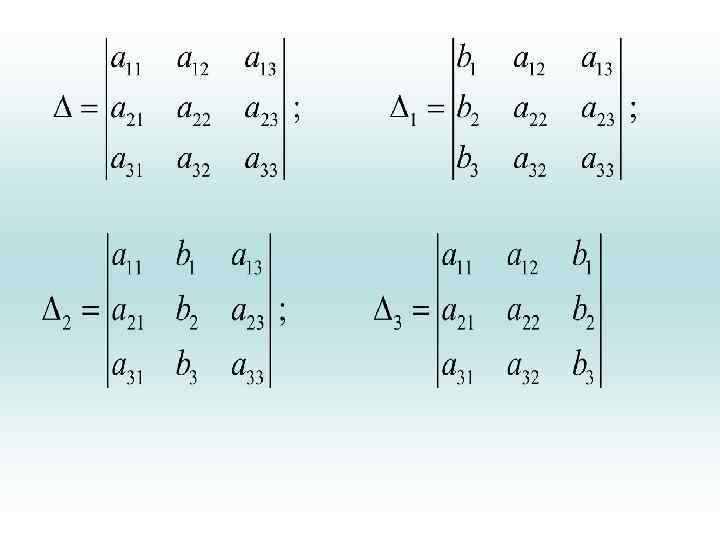
• Обратите внимание, что в определителе 1 первый столбец матрицы коэффициентов заменен на столбец свободных членов. В определителе 2 второй столбец матрицы заменен на столбец свободных членов и в определителе 3 последний столбец заменен на столбец свободных членов. Это надо запомнить.

• Из равенств (7) следует, что если 0, то решение определяется единственным образом (формулы Крамера):

ОПРЕДЕЛИТЕЛЬ НЕ РАВЕН НУЛЮ!

Решение системы уравнений методом Крамера ОТ ВЕТ

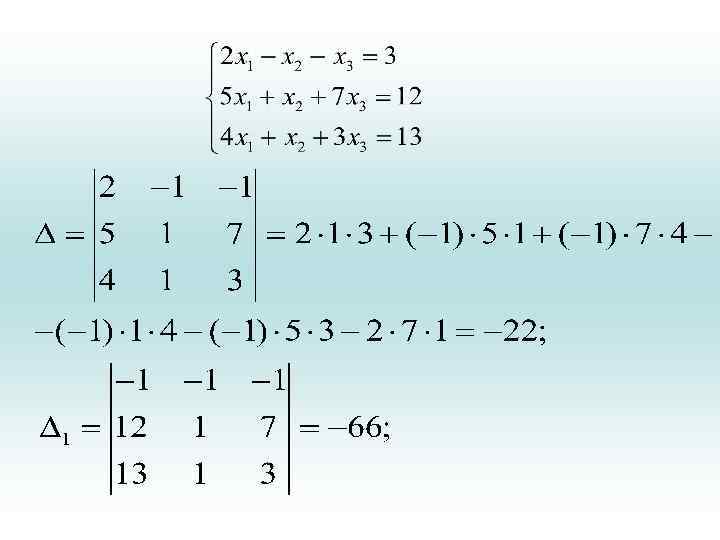
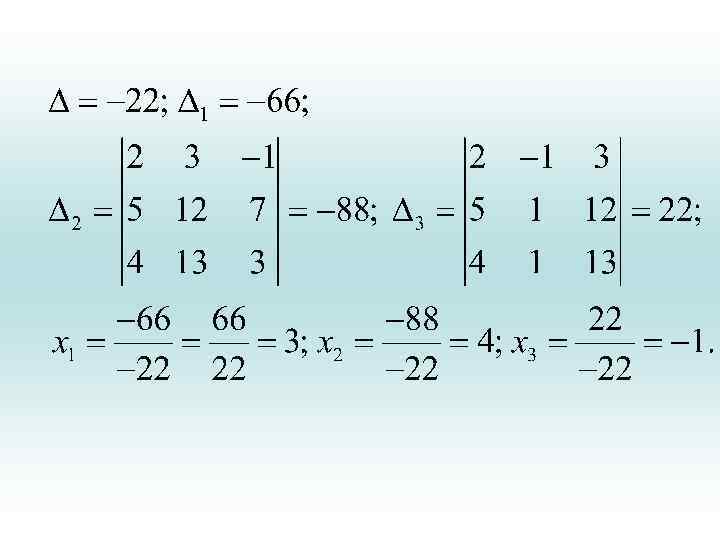
Ранг матрицы • Наибольший из порядков отличных от нуля миноров матрицы А называется рангом матрицы. Ранг матрицы обозначается rank(A) или r(А). Ранг матрицы А совпадает с рангом, определяемым по столбцам (строкам). Ранг матрицы (по строкам) равен максимальному числу линейно независимых строк. Аналогично по столбцам. Для любой матрицы ранг по строкам и ранг по столбцам совпадают. Например,

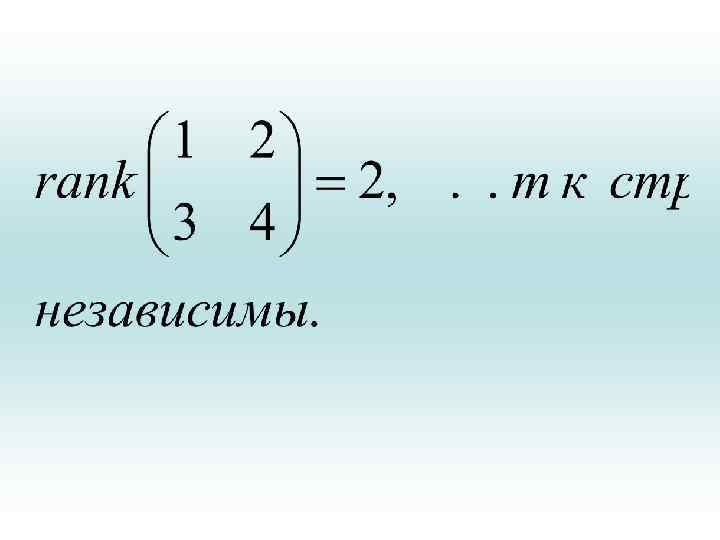
Теорема Кронекера-Капелли • Система линейных алгебраических уравнений совместна, если ранг матрицы системы равен рангу расширенной матрицы.