линейная алгебра 1.ppt
- Количество слайдов: 67

Линейная алгебра Лекция 2 доцент Старожилова О. В.

Линейная алгебра — часть алгебры, изучающая векторы, векторные, или линейные пространства и системы линейных уравнений. l Теория матриц была разработана в трудах Кэли (1850 -е). Написал более 700 работ. доказал теорему о том, что каждая квадратная матрица является корнем своего характеристического многочлена Артур Кэ ли 1821 - 1895) — английский математик 2 2/16/2018

l Системы линейных уравнений в матричном виде впервые появились в работах Лагерра (1867). Эдмо н Никола Лаге рр (1834 -1886) — французский математик, Труды по геометрии, комплексному анализу 3 2/16/2018

Понятие матрицы Матрица (размера тхn) - прямоугольная таблица чисел, содержащая т строк и n столбцов Наряду с круглыми скобками используются и другие обозначения матрицы: [ ], || ||. 4 2/16/2018

или, в сокращенной записи, l l 5 Величины, из которых состоит эта таблица, называются элементами матрицы обозначаются той же буквой, только строчной, что и матрица, с указанием номера строки (первый индекс) и номера столбца (второй индекс). 2/16/2018 А=(аij); i=1, 2, . . . , m; . . . , n. j = 1, 2,

Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n Матрица, состоящая из одной строки, называется матрицей-строкой, а из одного столбца-матрицейстолбцом 6 2/16/2018

Виды матриц Определение Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т. е. aij = bij для любых i=1, 2, . . . , m; j = 1, 2, . . . , n. Определение Квадратная матрица, независимо от ее порядка, называется единичной матрицей, если элементы ее главной диагонали равны единице, а все остальные элементы равны нулю. Такую матрицу обозначают 7 2/16/2018

Виды матриц Матрица получающаяся из матрицы A заменой строк столбцами (и наоборот), называется транспонированной матрицей. Симметрическая матрица - матрица, у которой AT= A или кососимметрической, если AT= -A. Нулевая матрица - матрица, все элементы которой равны нулю 8 2/16/2018

l Замечание Транспонирование – это перемена ролями строк и столбцов матрицы. Связь между матрицей и её транспонированной можно записать в виде . Пример Найти матрицу транспонированную данной 9 Замечание Матрица размера 1 х1, состоит из одного числа, отождествляется с этим числом. 2/16/2018

Теория определителей l Первоначально, определитель был представлен как собственно система линейных уравнений. Определитель «определял» имеет система одно или несколько возможных решений. Впервые определители использовать в Китае в 12 в. В Европе Крамер ввел положение о системах уравнений. Вандермонд представил определители в виде независимых функций, Лаплас создал общий метод разложения определителя на дополнительные миноры. Лагранж —изучал определители ( «результанты» ) в рамках теории исключения. Гаусс в в теории чисел, ввел термин «детерминант» 10 2/16/2018

ОПРЕДЕЛИТЕЛИ l Определитель (или детерминант) квадратной матрицы A - это число, которое ей сопоставимо и может быть вычислено по её элементам. l Совокупность элементов квадратной матрицы, расположенных на отрезке, соединяющем левый верхний угол с правым нижним, называют главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним, - побочной диагональю. Пример Найти элементы, лежащие на главной диагонали матрицы Решение 11 2/16/2018

Исследование системы двух линейных уравнений l Рассмотрим систему двух линейных уравнений с двумя неизвестными: Найдем решение Таким образом, если то система имеет единственное решение. 12 2/16/2018

Понятие определителя 2 -го порядка Определитель второго порядка, соответствующий таблице элементов , определяется равенством где a 1 и b 2 – элементы главной диагонали, a 2 и b 1 – элементы побочной диагонали Пример 13 2/16/2018

Определитель второго порядка l вычисляется по следующему правилу: равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали вычисление определителя 2 -го порядка -схема 14 2/16/2018

Определители 3 -го порядка, вычисление и свойства Определитель третьего порядка, соответствующий таблице элементов , определяется равенством a 1 b 2 c 3+ a 2 b 3 c 1+ a 3 b 1 c 2 - a 3 b 2 c 1 - a 1 b 3 c 2 - a 2 b 1 c 3 где a 1 , b 2 и c 3 – элементы главной диагонали, a 3 , , b 2 и c 1 – элементы побочной диагонали 15 2/16/2018
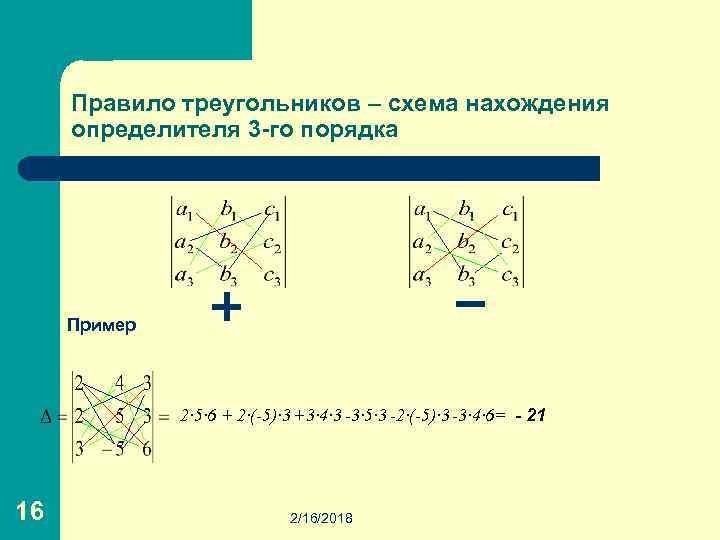
Правило треугольников – схема нахождения определителя 3 -го порядка Пример 2∙ 5∙ 6 + 2∙(-5)∙ 3 +3∙ 4∙ 3 -3∙ 5∙ 3 -2∙(-5)∙ 3 -3∙ 4∙ 6= - 21 16 2/16/2018

Правило треугольников l 17 При вычислении определителя 3 -го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так 2/16/2018

Пример l Решить уравнение Решение 18 2/16/2018

Свойства определителей 1. Значение определителя не изменится, если строки определителя заменить столбцами, а столбцы – соответствующими строками. l. При транспонировании определитель матрицы не меняется l( «равноправие» строк и столбцов определителя) 19 2/16/2018

Свойства определителей (продолжение) 2. Общий множитель элементов какой-нибудь строки (или столбца) может быть вынесен за знак определителя. 3. Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца), то определитель равен нулю 20 2/16/2018

Свойства определителей (продолжение) l 4. При перестановке двух строк (столбцов) определитель меняет знак на противоположный 1. 5. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответственные элементы другой строки (столбца), умноженные на одно и тоже число. 21 2/16/2018

Свойства определителей (продолжение) l 6. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю. 7. Сумма произведений элементов одной строчки матрицы на алгебраические дополнения соответствующих элементов другой строчки равна нулю 22 2/16/2018

8. Если каждый элемент столбца или строки представляет собой сумму двух слагаемых, то такой определитель может быть представлен в виде суммы двух определителей, у одного из которых соответствующий столбец составлен из первых слагаемых, а у второго – из вторых. 23 2/16/2018

l 24 9. Если матрицы n -го порядка имеет две пропорциональные строчки (или столбца), то ее определитель равен нулю 2/16/2018

Пример Вычислить определитель 3 -го порядка Так как элементы 2 -ой и 3 -ей строки одинаковы, то определитель равен 0. 25 2/16/2018

СЛАУ l l l 26 Крамер Габриэль (17041752) швейцарский математик, родился в Женеве, основные работы относятся к высшей алгебре и аналитической геометрии, установил правила решения систем линейных уравнений с неизвестными, заложил основы теории определителей. основоположник линейной алгебры 2/16/2018

Правило Крамера – метод решения системы линейных уравнений 27 2/16/2018

Правило Крамера l Δ≠ 0– система имеет единственное решение - формулы Крамера l Δ=0, Δx≠ 0, Δу ≠ 0, Δz ≠ 0 - система не имеет решения l Δ=0, Δx=0, Δу =0, Δz =0 -система имеет бесконечное множество решений Замечание Правило Крамера остается справедливым и для линейных систем уравнений с 28 неизвестными при любом 2/16/2018

29 2/16/2018

30 2/16/2018

l Определение Система, не имеющая ни одного решения, называется несовместной или неопределенной. l Определение Система, обладающая хотя бы одним решением, называется совместной или определенной Пример Решить систему уравнений Ответ: решений нет Почему ? ? ? 31 2/16/2018

Пример l Решить систему уравнений Ответ: бесчисленное множество решений вида 32 2/16/2018

Геометрическое истолкование результатов исследования системы 33 2/16/2018

Понятие определителя n-го порядка. Определителем n-го порядка называется число Δ, образованное из n 2 чисел aij(элементов), расположенных в квадратной таблице из n строк и n столбцов, следующим образом 34 2/16/2018

l Определитель n-го порядка равное сумме членов Замечание Число сомножителей в каждом произведении равно порядку матрицы. Определение Матрица невырожденная - квадратная матрица имеющая определитель, отличный от нуля в противном случае - матрица вырожденная или особая. Замечание Определитель бывает только у квадратных матриц. Замечание Иногда вместо термина определитель используют термин детерминант 35 2/16/2018

Определитель Вандермонда l l 36 Вандермонд Александр (1735 -1796) – франц. математик. Родился в Париже. Предложив специальный символ определителя изложил теорию детерминантов Его труды были забыты во Франции и обратил внимание Л. Кронекер (немецкий математик уже через 100 лет, он также занимался системами линейных уравнений). 2/16/2018

Вычисление определителя Вандермонда 37 2/16/2018

Минором Мij элемента aij определителя n-го порядка называется определитель (n-1)-го порядка который получается путем вычеркивания в исходном определителе строки и столбца, содержащих элемент aij. Алгебраическим дополнением Аij элемента aij определителя n-го порядка называется его минор, умноженный на (-1) i+j Аij=(-1) i+j Мij 38 2/16/2018

Пример l Дан определитель Замечание Определитель всякой матрицы есть число, то миноры элементов матрицы также являются числами Замечание Каждый элемент матрицы является ее минором 1 -го порядка 39 2/16/2018

Замечание Пример l Минор берется со своим знаком, если сумма его индексов четна, и с обратным, если сумма нечетна. Дан определитель Найти алгебраическое дополнение Замечание Для элементов, расположенных на главной диагонали, алгебраическое дополнение совпадает с минором 40 2/16/2018

Теорема Лапласа (разложение по строке) Разложение называется разложением определителя по элементам Пример разложение элементам второй строки Каждый определитель равен сумме произведений элементов любой его строки(столбцов) на их алгебраические дополнения, т. е. 41 2/16/2018

Пример: Вычислить определитель, разлагая его по элементам второго столбца 42 2/16/2018

Методы вычисления определителей l l 43 для численных определителей – получение нулей в какой-нибудь строчке и сведение к одному определителю на единицу меньшого порядка преобразование матрицы определителя к треугольному виду. 2/16/2018

Обобщение формулы Крамера на случай системы n линейных уравнений. Из коэффициентов при неизвестных составим определитель, т. е. 44 2/16/2018

l 45 Главный определитель системы - определитель главной матрицы системы, составленной из коэффициентов при неизвестных: 2/16/2018

l 46 Если в главном определителе системы заменить поочередно столбцы коэффициентов при неизвестных на столбец свободных членов, то получим n дополнительных определителей (для каждого из n неизвестных): 2/16/2018

Разрешимость системы l 47 При этом важен вопрос о разрешимости данной системы, который решается сравнением главного и дополнительных определителей системы с нулем: 2/16/2018

Алгоритм решения методом Крамера l l 2. Вычисляют главный определитель системы: l 48 1. Записывают систему в матричном виде. 2/16/2018

l 49 3. Вычисляют все дополнительные определители системы: 2/16/2018

l l 4. Если главный определитель системы не равен нулю, то выполняют пункт 5. Иначе рассматривают вопрос о разрешимости данной системы (имеет бесчисленное множество решений или не имеет решений). l 5. Находят значения всех неизвестных по формулам Крамера 50 2/16/2018

Варианты решений Если для системы уравнений определитель Δ≠ 0, то система имеет единственное решение где определитель Δi - полученный из определителя Δ заменой i-го столбца на столбец свободных членов. 51 2/16/2018

Пример: Решить систему линейных уравнений Вычислим определитель системы 52 2/16/2018

Поскольку ∆ ≠ 0, система уравнений может быть решена по формулам Крамера. Найдем определители ∆x 1 – ∆x 4: 53 2/16/2018

Таким же образом высчитываем ∆х4 и получаем: ∆х1 = ∆х2 = –∆х3 = ∆х4, и, следовательно, х1 = х2 = –х3 = х4 = 1. 54 2/16/2018

Система двух линейных уравнений с тремя неизвестными. l l 55 Если a 1/a 2=b 1/b 2=c 1/c 2, то система сводится к одному уравнению (например, первому), из которого одно выражается через два других, значения которых остаются произвольными. Если a 1/a 2=b 1/b 2=c 1/c 2 не выполнено, то решения системы находятся по формулам 2/16/2018

Система трех однородных линейных уравнений с тремя неизвестными. Линейное уравнение называется однородным, если его свободный член равен нулю. Система линейных уравнений называется однородной, если все входящие в нее уравнения являются линейными однородными уравнениями. Если определитель отличен от нуля, то она имеет единственное решение x=0, y=0, z=0. В противном случае она имеет бесконечное множество решений 56 2/16/2018

Метод Крамера l l l 57 Преимущества метода: - простой метод; - независимость вычислений определителей, следовательно, процесс вычисления определителей может быть распараллелен. Недостатки метода: - высокая ресурсоемкость вычислений определителей; - чувствительность к ошибкам округления. 2/16/2018

Решение системы уравнений с помощью Mathcad – – 58 Чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания. Затем щелкните по кнопке Matrix or Vector Toolbar в панели математических инструментов, чтобы открыть панель операций с матрицами и векторами. определите число строк (Rows) и число столбцов (Columns) и закройте окно диалога, Ok. 2/16/2018

l l 59 Определим матрицу системы A и матрицу правой части b: Найдем по формулам Крамера решение системы линейных уравнений 2/16/2018

l Вычислим определитель матрицы системы A Для нахождения определителя матрицы, воспользуйтесь нопкой Determinant в панели Matrix or Vector Toolbar Для просмотра результата введите знак равенства, используя клавишу <=>. 60 2/16/2018
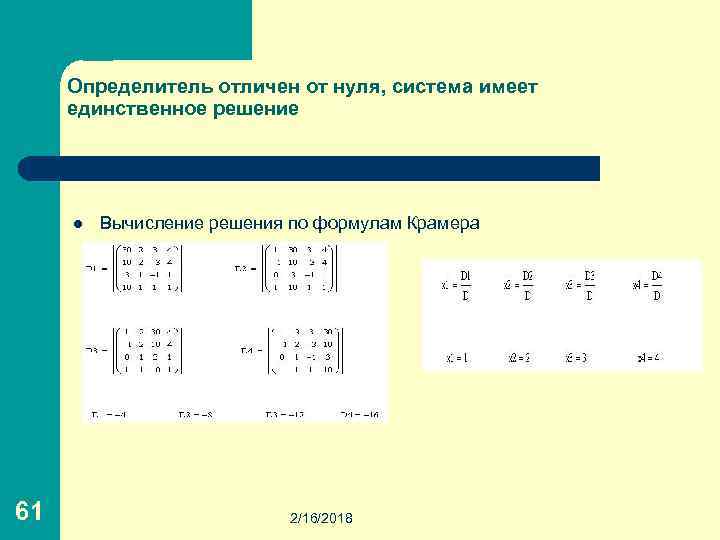
Определитель отличен от нуля, система имеет единственное решение l 61 Вычисление решения по формулам Крамера 2/16/2018

ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМЫ LSOLVE Для численного решения линейных систем уравнений в Math. CAD имеется специальная функция : lsolvе(A, B) l Она решает систему линейных алгебраических уравнений вида А x X =B, выдавая решение - вектор X. А - матрица коэффициентов размерности nxn; В - вектор свободных членов размерности n ; X - вектор неизвестных решений l 62 2/16/2018

Пример 63 2/16/2018

ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМЫ GIVEN - FIND l l l l 64 solve block (Блок решения) удобен для решения системы уравнений. Синтаксис Блока решения: Given Уравнения Ограничительные условия Find(v 1, v 2, . . . vn) - возвращает значение одной или ряда переменных для точного решения 2/16/2018

l l l 65 Задаем начальное приближение Заключаем уравнения в блок решения, начинающийся ключевым словом Given и заканчивающийся ключевым словом Find(v 1, v 2, . . . vn). после слова Find(v 1, v 2, . . . vn) ввести знак равенства [=], Math. ACD выдаст численное решение 2/16/2018

Используя вычислительный Given/Find 66 2/16/2018

Литература l l l l 67 Щипачев В. С. Высшая математика. Учебн. Для вузов. 3 -е изд. , стер. -М. , Высшая школа. 1996 -479 с. Данко П. Е. , Попов А. Г. , Кожевников Т. Я. , Высшая математика в упражнениях и задачах, ч. 1, 2, М. В. Ш. , 1996 г. Гурман В. Е. Руководство к решению задач по теории вероятностей и математической статистики. Высшая школа. 1979 г. Ильин В. А. , Позняк Э. Г. Аналитическая геометрия. Н. , 1988 – 223 с. Каплан И. А. Практические занятия по высшей математике. Харьков, 1980 г. Пискунов Н. П. Дифференциальное и интегральное исчисление по математике для вузов. М. , 1970 г. , 1985 г. , т. 1, 2 Бугров Я. С. , Никольский С. М. Высшая математика. Дифференциальное и интегральное исчисление. М. , 1980 г. , 1984 г. 2/16/2018
линейная алгебра 1.ppt