Линейная алгебра.ppt
- Количество слайдов: 30

Линейная алгебра • 1. Вектор: определения; свойства • 2. Матрицы: классификация; свойства, операции • 3. Числовые характеристики матриц: определитель, минор, алгебраическое дополнение, след, ранг • 4. Системы линейных алгебраических уравнений: формы записи, классификация, решение систем ЛАУ • 1

1. Вектор: определения Вектор размера n – совокупность n чисел, заданных в определенном порядке. Имя вектора – любая латинская или греческая буква, например а, х, у. Обозначается a = (a 1 , a 2 , …. an). Числа a 1 , a 2 , …. an – компоненты вектора; n - его размерность. Единичный вектор – все его компоненты равны 1. Обозначается 1 Нуль-вектор - все его компоненты равны 0. Обозначается 0. Противоположный вектор – a = (-a 1, -a 2 , …. -an). Очевидно a +(– a) =0 2

1. Вектор: основные операции: 1. Алгебраическая сумма двух векторов = алгебраической сумме их компонент 2. Умножение вектора на число – умножение каждой компоненты на это число 3. Скалярное произведение двух векторов – число, равное сумме произведений одноименных координат данных векторов • < a, b > = a 1 b 1 + a 2 b 2 +…anbn • Основные свойства скалярного произведения: – < a, b >=< b , a>; – β< a, b >= < βa, b > ; – < a+ b, с>=< a, с>+ <b, с> ; – < a, a> >=0 3
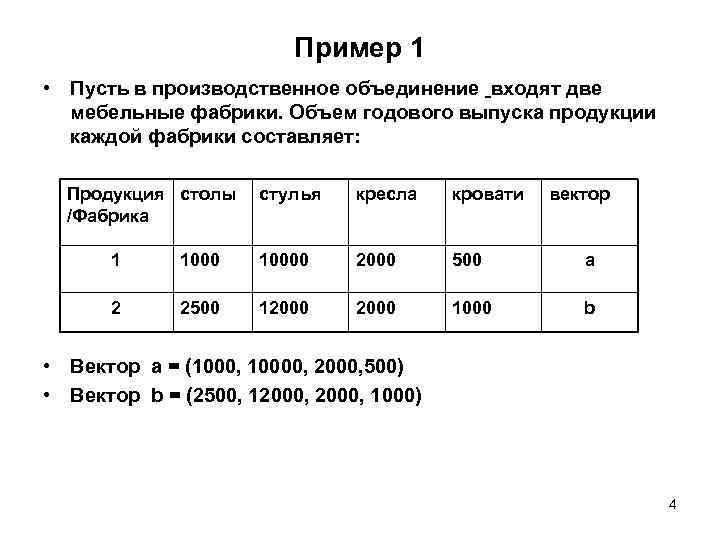
Пример 1 • Пусть в производственное объединение входят две мебельные фабрики. Объем годового выпуска продукции каждой фабрики составляет: Продукция столы /Фабрика стулья кресла кровати вектор 1 10000 2000 500 a 2 2500 12000 1000 b • Вектор a = (1000, 10000, 2000, 500) • Вектор b = (2500, 12000, 1000) 4

Матрицы. Определения Матрица размера m x n – совокупность чисел прямоугольной таблицы, состоящей из m строк и n столбцов. Обозначается А= или А=(a I, j), i=1, 2…m; j= 1, 2…n Числа a i, J – элементы матрицы, строки и столбцы – ее ряды. Множество всех матриц размера m x n обозначается Rmxn, А= Rmxn 5

Основные определения и свойства матриц 1. Две матрицы А и В одного и того же размера равны, если равны соответствующие элементы, аi, j = bi, j 2. Вектор – столбец – матрица, состоящая из одного столбца 3. Вектор – строка – матрица, состоящая из одной строки 4. Нулевая матрица – все ее элементы =0; обозначатся Оmxn 5. Квадратная матрица – m=n (число строк равно числу столбцов) 6. Главная диагональ квадратной матрицы – элементы аi, i , лежащие на главной диагонали 7. Треугольная матрица – квадратная матрица, такая, что все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю. 8. Единичная матрица Е – все элементы на главной диагонали аi, I =1, остальные элементы равны нулю. 6

Основные определения и свойства матриц 9. Транспонированная матрица Аt – матрица, полученная из исходной матрицы А заменой строк на столбцы с сохранением порядка. 10. Сумма двух матриц C=A+B , А= (аi, j) и В= (bi, j ) одного и того же размера – матрица С = (сi, j ) того же размера, элементы которой равны сумме соответствующих элементов исходных матриц – сi, j= аi, j+ bi, j: C=A-B сi, j= аi, j – bi, j 11. Произведение матрицы на число – все элементы исходной матрицы умножаются на это число. В=2 А (bi, j =2 ai, j ). Очевидное следствие : общий множитель всех элементов матрицы можно выносить за знак матрицы 12. Произведение двух матриц А и В. Произведение имеет смысл, если число столбцов первого сомножителя (например, А) совпадает с числом строк второго сомножителя (например, В). Пусть А= Rmxn , В= Rnxk, тогда С = АВ = Rmxk. 7

Основные свойства произведения матриц Операция произведения двух матриц обладает следующими свойствами: 1. (AB)C= A(BC); α(AB)= (αA)B; (A+B)C=AC+BC; 2. (AB)t = Bt At ; 3. AE=EA=A 4. AB ≠BA в общем случае. Если AB = BA, то матрицы A и B называются перестановочными. 5. Квадратную матрицу А можно возвести в квадрат, куб, в к –ую степень, получить Ак 6. А 0 =Е 8

Пример 2. Предприятие выпускает продукцию трех видов Р 1, Р 2, Р 3 и использует сырье двух типов S 1 и S 2. Матрица А 3 х2 (технологическая). Показывает, сколько единиц сырья jго типа расходуется на производство продукции i-го вида. План выпуска продукции задан вектором- строкой С, Стоимость единицы сырья каждого типа задается вектором – столбцом В А= С= В= Матрица – строка затрат сырья S =CA= Общая стоимость сырья Q = SB = =730*30 + 980*50 = 70900 (ден. ед. ) 9

Основные числовые характеристики квадратных матриц. Определитель 1. Определитель квадратной матрицы Anxn – число, которое вычисляется по определенным правилам Определитель обозначается det или. 2. Основные правила вычисления определителей: 1) Определитель диагональной матрицы равен произведению диагональных элементов 2) Общий множитель строки можно вынести за знак определителя 3) Если к одной из строк прибавить другую строку (к одному из столбцов прибавить другой столбец), то определитель не измениться 4) Если все элементы строки (столбца) равны нулю, то определитель равен нулю 10

Основные числовые характеристики квадратных матриц. Определитель 5) Если к строке матрицы прибавить другую строку матрицы, у множенную на число, то определитель не измениться 6) Если поменять местами две строки (два столбца) матрицы, то ее определитель поменяет знак 7) Если матрица имеет две одинаковые строки ( два одинаковых столбца), то определитель равен нулю 8) В общем случае определитель вычисляется разложением по элементам строки (столбца). Для этого вычисляют соответствующие миноры и алгебраические дополнения Запомните: Квадратная матрица, определитель которой равен нулю называется вырожденной. Основные числовые характеристики – след матрицы След матрицы – сумма элементов главной диагонали. Обозначается tr A = 11

Обратная матрица • Пусть А – квадратная матица. Если существует матрица В, такая, что АВ=Е, то говорят, что В – обратная матрица. • Обратную матрицу обозначают А-1. • Обратная матрица перестановочна с исходной, • т. е А А-1 = А-1 А = Е • Очевидно, (А А-1)-1 =А 12

Прямоугольная матрица. Числовые характеристики 1. В прямоугольной матрице Аmxn число строк m не равно числу столбцов n, m≠n 2. Минор к-го порядка матрицы Аmxn - определитель квадратной подматрицы, полученной из основной выделением к строк и к столбцов 3. Алгебраическое дополнение элемента ai, j квадратной матрицы равно Ai, j = (-1)i+j . Здесь - минор, полученный из основной матрицы вычеркиванием i –ой строки и j-го столбца. 3. Ранг матрицы r(A) - наибольший из порядков миноров данной матрицы, отличных от нуля. Выполняется соотношение 0≤ r(A)≤min (m, n) Минор порядка r называется базисным 13

Системы линейных алгебраических уравнений Система из m уравнений первой степени с n неизвестными может быть записана (*) Или в матричной форме AX = b (*) где A=(ai, j) – матрица коэффициентов при неизвестных системы, X – вектор неизвестных системы, b – вектор свободных членов. Система (*) называется однородной, если все bi равны нулю. В противном случае система неоднородна. Система является совместной, если она имеет решение и несовместной (противоречивой) в противном случае. 14

Решение системы ЛАУ Решением системы (*) являетс любая совокупность чисел β 1, β 2, …. βn, , если при их подстановке в уравнение системы на Место соответствующих неизвестных все уравнения обращаются в тождества. Решение (β 1, β 2, …. βn) неотрицательно, если все его компоненты неотрицательны. Матрица • • • = называется расширенной матрицей системы. Система линейных алгебраических уравнений совместна только тогда, когда ранг матрицы А равен рангу матрицы (теорема Кронекера – Капели. ) 15

Решение систем ЛАУ Для множества решений системы (*) имеются три возможности: 1). Система не имеет решения, система несовместна – r(A)≠r( ) 2). Система имеет единственное решение, система определена r(A)=n 3). В случае r(A)<n, система имеет бесчисленное множество решений (неопределенная система). В этом случае r переменных (базисные переменные) выражаются через n- r переменных (свободные переменные). 16

Методы решения систем ЛАУ • Существует несколько способов решения системы линейных алгебраических уравнений (СЛАУ). • 1. Метод Крамера. Применяется для решения невырожденных матриц (определитель системы не равен нулю • 2. Метод обратной матрицы • 3. Метод Гаусса , метод исключения переменных. Является универсальным методом решения СЛАУ. • 4. Метод Жордана – Гаусса. Модификация метода Гаусса. Применяется для решения задач, в которых m<n. Позволяет найти базисные и свободные переменные СЛАУ • 5. Численные методы последовательных приближений 17

1. Метод Крамера Описание. Примеры • Для системы линейных уравнений с n неизвестными с определителем , отличным от нуля. Решение записывается в виде 18

1. Метод Крамера Описание. Примеры Система линейных уравнений: Определители Решение 19

1. Метод Крамера. Пример 3 • Дана СЛАУ • Определители • Решение 20

2. Метод обратной матрицы • Применяется для решения невырожденных СЛАУ с числом уравнений, равным числу переменных, m=n. • Вычисляют определитель и обратную матрицу системы. Тогда вектор неизвестных X равен • • X = A -1 B 21

2. Метод обратной матрицы. Пример 4 Пусть СЛАУ имеет вид Тогда Решение системы 22

Метод Гаусса (метод исключения переменных) Может применяться как в случае, когда m=n, так и m≠n. Метод заключается в последовательном исключении переменных, к преобразованию исходной системы к верхне-треугольному виду. Рассмотри применение метода на примерах. Пример 5. Рассмотрим решение примера 4 методом Гаусса 23

Общее, базисное, частное решение СЛАУ В общем случае СЛАУ имеет размерность mxn (m – число уравнений, n – число переменных) В зависимости от соотношения m и n возникают различные классы задач, Рассмотрим случай m < n , число уравнений меньше числа неизвестных. 1. r < m - уравнения системы зависимые 2. r = m - уравнения системы независимые 3. r(A)≠r( ) – система несовместная 4. r(A) = r( )= r – система совместная 5. r < n – система совместная, неопределенная, имеет бесконечное количество решений. Базисные и свободные (независимые) переменные 6. r = n – система определенная, совместная. Имеет единственное решение 24

Базисные и свободные переменные Рассматривается случай m < n , система совместная, r < n Базисные (основные ) переменные - r переменных, которые могут быть выражены через ( n-r) свободных (неосновных) переменных. Базисные переменные должны входить в полный набор разрешенных переменных. К разрешенным относят переменные, входящие только в одно уравнение с коэффициентом 1, а в другие уравнения – коэффициентом 0. Например, в примере ниже разрешенными, а, следовательно, базисными, могут быть переменные x 1, x 2 , x 5. С другой стороны ранг системы r = 2, Следовательно есть два набора базисных переменных (x 1, x 2 ) и ( x 2 , x 5 ) 25

Базисные и свободные переменные Продолжим рассмотрение примера. Выберем в качестве базисных переменные x 1 и x 2 Тогда общее решение будет выглядеть так: Приравняв свободные переменные к нулю, получим базисное решение Приравняв свободные переменные произвольным константам, получим одно их частных решений, например X 3 =0, X 4=1, X 5=2 получим 26

Элементарные преобразования СЛАУ приводятся к равносильным разрешенным системам с помощью элементарных преобразований 1. Если какое-либо уравнение системы умножить на некоторое отличное от нуля число, а остальные уравнения оставить без изменения, то получится система, равносильная данной. 2. Если к какому-либо уравнению системы прибавить другое, а все остальные уравнения оставить без изменения, то получится система, равносильная данной 3. Если к какому-либо уравнению прибавить другое, умноженное на некоторое число, а все остальные уравнения оставить без изменения, то получится система, равносильная данной. 4. Если система уравнений содержит тривиальное уравнение, то его можно исключить из системы, при этом получится система равносильная исходной. 27

Метод Жордана-Гаусса решения СЛАУ • Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке: • 1. Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна. • 2. Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают. • 3. Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения. • 4. Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом. • 5. Далее заново переходят к пункту 1 28

Пример решения СЛАУ по методу Жордана- Гаусса Найти: два общих и два соответствующих базисных решения Таблица решения 29

Продолжение решения примера: Равносильная система с разрешенными неизвестными и Общее решение Приравняв x 3=0, x 4=0 получим базисное решение (один из вариантов) Чтобы найти другое базисное решение при пересчете исходной системы следует выбрать другой разрешающий элемент. Число общих и соответствующих базисных решений исходной системы равно числу сочетаний 30
Линейная алгебра.ppt