ea26ae3e8f8b361ae3673481f29e281e.ppt
- Количество слайдов: 27
 LINEARNO PROGRAMIRAWE I SIMPLEKS METOD Marko Petkovi} (Mapet, De. Xter, itd )
LINEARNO PROGRAMIRAWE I SIMPLEKS METOD Marko Petkovi} (Mapet, De. Xter, itd )
 1. UVOD § Linearno programirawe je deo {iroke matemati~ke oblasti (Operaciona istra`ivawa) § Zadatak: Odre|ivawe optimalne vrednosti ciqne funkcije pri zadatim ograni~ewima § Prvi rad iz operacionih istra`ivawa objavio Kantorovi~ 1939. § Prvi rad u na{oj dr`avi je objavio pukovnik Vlastimir Ivanovi} 1940 god pod naslovom “Pravila za prora~un potrebnog broja transportnih sredstava”. § Prvi op{ti metod za re{avawe problema linearnog programirawa je objavio Dancig 1947 (Simpleks metod). § Prvi polinomijalni metod je objavio Ha~ijan 1979. § Kasnije (1984 -1990) otkriveni su metodi unutra{we ta~ke (Interior point metodi) na kojima se danas baziraju najmo}niji solveri (PCx, Lip. Sol, HOPDM, etc).
1. UVOD § Linearno programirawe je deo {iroke matemati~ke oblasti (Operaciona istra`ivawa) § Zadatak: Odre|ivawe optimalne vrednosti ciqne funkcije pri zadatim ograni~ewima § Prvi rad iz operacionih istra`ivawa objavio Kantorovi~ 1939. § Prvi rad u na{oj dr`avi je objavio pukovnik Vlastimir Ivanovi} 1940 god pod naslovom “Pravila za prora~un potrebnog broja transportnih sredstava”. § Prvi op{ti metod za re{avawe problema linearnog programirawa je objavio Dancig 1947 (Simpleks metod). § Prvi polinomijalni metod je objavio Ha~ijan 1979. § Kasnije (1984 -1990) otkriveni su metodi unutra{we ta~ke (Interior point metodi) na kojima se danas baziraju najmo}niji solveri (PCx, Lip. Sol, HOPDM, etc).
 2. PROBLEM LINEARNOG PROGRAMIRAWA
2. PROBLEM LINEARNOG PROGRAMIRAWA
 Problem linearnog programirawa u standardnom obliku
Problem linearnog programirawa u standardnom obliku
 2. 2. Va`nije osobine skupa dopustivih re{ewa
2. 2. Va`nije osobine skupa dopustivih re{ewa

 3. SIMPLEKS METOD
3. SIMPLEKS METOD


 Kona~no, jedan primer ; )
Kona~no, jedan primer ; )
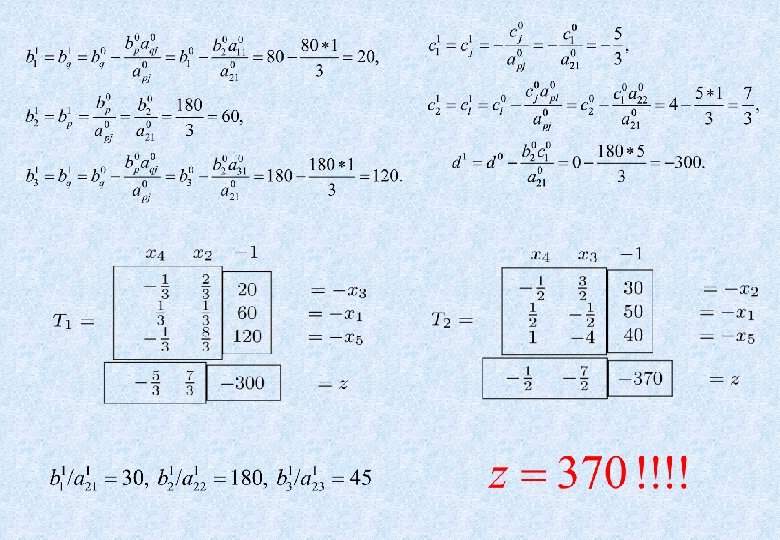
 Simpleks metod i degenerisana re{ewa Razmotrimo Takerovu tabelu: Posle transformacija pomo}u gorwih pivot elemenata ponovo dobijamo polaznu Takerovu tabelu. Pri tome je vrednost funkcije ciqa stalno 0.
Simpleks metod i degenerisana re{ewa Razmotrimo Takerovu tabelu: Posle transformacija pomo}u gorwih pivot elemenata ponovo dobijamo polaznu Takerovu tabelu. Pri tome je vrednost funkcije ciqa stalno 0.

 Odre|ivawe po~etnog bazi~no dopustivog re{ewa
Odre|ivawe po~etnog bazi~no dopustivog re{ewa

 Odre|ivawe po~etnog bazi~nog re{ewa (Eliminacija jedna~ina)
Odre|ivawe po~etnog bazi~nog re{ewa (Eliminacija jedna~ina)


 Modifikacija Algoritma S 3 za transformaciju tabele u bazi~no dopustivu
Modifikacija Algoritma S 3 za transformaciju tabele u bazi~no dopustivu



 Poboq{awe Algoritma S 1 za zamenu promenqivih
Poboq{awe Algoritma S 1 za zamenu promenqivih
 3. IMPLEMENTACIJA Sastoji se iz slede}ih faza: § § § U~itavawe problema (MPS format) Presolver Implementacija algoritma S 4 Implementacija algoritma S 3 Implementacija algoritma S 2 [tampawe rezultata (status problema, optimalna vrednost ciqne fje i ta~ka u kome se ona dosti`e
3. IMPLEMENTACIJA Sastoji se iz slede}ih faza: § § § U~itavawe problema (MPS format) Presolver Implementacija algoritma S 4 Implementacija algoritma S 3 Implementacija algoritma S 2 [tampawe rezultata (status problema, optimalna vrednost ciqne fje i ta~ka u kome se ona dosti`e
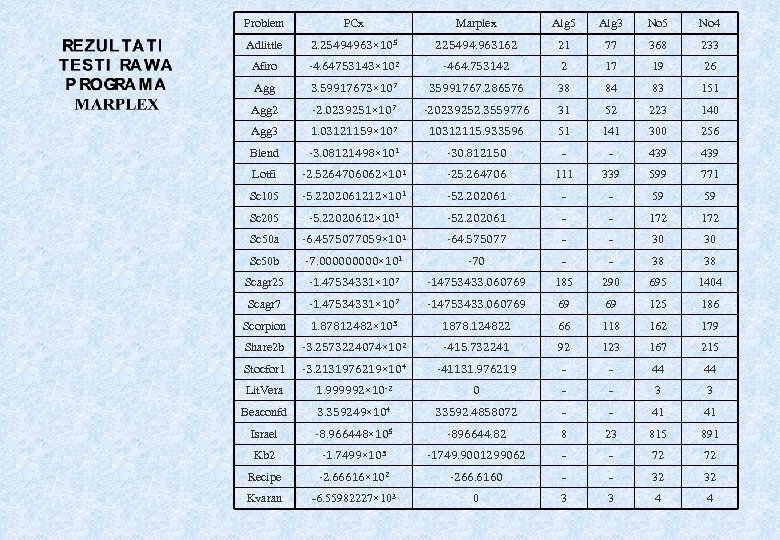 Problem PCx Marplex Alg 5 Alg 3 No 5 No 4 Adlittle 2. 25494963× 105 225494. 963162 21 77 368 233 Afiro -4. 64753143× 102 -464. 753142 2 17 19 26 Agg 3. 59917673× 107 35991767. 286576 38 84 83 151 Agg 2 -2. 0239251× 107 -20239252. 3559776 31 52 223 140 Agg 3 1. 03121159× 107 10312115. 933596 51 141 300 256 Blend -3. 08121498× 101 -30. 812150 - - 439 Lotfi -2. 5264706062× 101 -25. 264706 111 339 599 771 Sc 105 -5. 2202061212× 101 -52. 202061 - - 59 59 Sc 205 -5. 22020612× 101 -52. 202061 - - 172 Sc 50 a -6. 4575077059× 101 -64. 575077 - - 30 30 Sc 50 b -7. 00000× 101 -70 - - 38 38 Scagr 25 -1. 47534331× 107 -14753433. 060769 185 290 695 1404 Scagr 7 -1. 47534331× 107 -14753433. 060769 69 69 125 186 Scorpion 1. 87812482× 103 1878. 124822 66 118 162 179 Share 2 b -3. 2573224074× 102 -415. 732241 92 123 167 215 Stocfor 1 -3. 2131976219× 104 -41131. 976219 - - 44 44 Lit. Vera 1. 999992× 10 -2 0 - - 3 3 Beaconfd 3. 359249× 104 33592. 4858072 - - 41 41 Israel -8. 966448× 105 -896644. 82 8 23 815 891 Kb 2 -1. 7499× 103 -1749. 9001299062 - - 72 72 Recipe -2. 66616× 102 -266. 6160 - - 32 32 Kvaran -6. 55982227× 103 0 3 3 4 4
Problem PCx Marplex Alg 5 Alg 3 No 5 No 4 Adlittle 2. 25494963× 105 225494. 963162 21 77 368 233 Afiro -4. 64753143× 102 -464. 753142 2 17 19 26 Agg 3. 59917673× 107 35991767. 286576 38 84 83 151 Agg 2 -2. 0239251× 107 -20239252. 3559776 31 52 223 140 Agg 3 1. 03121159× 107 10312115. 933596 51 141 300 256 Blend -3. 08121498× 101 -30. 812150 - - 439 Lotfi -2. 5264706062× 101 -25. 264706 111 339 599 771 Sc 105 -5. 2202061212× 101 -52. 202061 - - 59 59 Sc 205 -5. 22020612× 101 -52. 202061 - - 172 Sc 50 a -6. 4575077059× 101 -64. 575077 - - 30 30 Sc 50 b -7. 00000× 101 -70 - - 38 38 Scagr 25 -1. 47534331× 107 -14753433. 060769 185 290 695 1404 Scagr 7 -1. 47534331× 107 -14753433. 060769 69 69 125 186 Scorpion 1. 87812482× 103 1878. 124822 66 118 162 179 Share 2 b -3. 2573224074× 102 -415. 732241 92 123 167 215 Stocfor 1 -3. 2131976219× 104 -41131. 976219 - - 44 44 Lit. Vera 1. 999992× 10 -2 0 - - 3 3 Beaconfd 3. 359249× 104 33592. 4858072 - - 41 41 Israel -8. 966448× 105 -896644. 82 8 23 815 891 Kb 2 -1. 7499× 103 -1749. 9001299062 - - 72 72 Recipe -2. 66616× 102 -266. 6160 - - 32 32 Kvaran -6. 55982227× 103 0 3 3 4 4
 Prednosti i nedostaci Simpleks metoda Prednosti: a. Jednostavnost a. Mo`e da se koristi i u obli-ku ra~unarskog programa i bez ra~unara (za mawe primere) a. Boqa stabilnost u slu~aju lo{e uslovqenih problema linearnog programirawa a. Ne postoji nagomilavawe numeri~kih gre{aka kod Revidiranog simpleks metoda a. Velika brzina izvr{avawa za veliki broj problema u prak-si (i pored velike slo`e-nosti) Nedostaci: a. Slo`enost algoritma nije polinomijalna (Minti i Kli su konstruisali primer na kome Simpleks dosti`e NP slo`enost a. Nedovoqno iskori{}ewe ret-ko}e polazne matrice prob-lema (nemogu}nost primene za probleme ekstremno velike dimenzije) a. Nagomilavawe numeri~ke gre{ke (izbegava se revidiranom Simpleks metodom, koji je mawe stabilan i znatno spo-riji)
Prednosti i nedostaci Simpleks metoda Prednosti: a. Jednostavnost a. Mo`e da se koristi i u obli-ku ra~unarskog programa i bez ra~unara (za mawe primere) a. Boqa stabilnost u slu~aju lo{e uslovqenih problema linearnog programirawa a. Ne postoji nagomilavawe numeri~kih gre{aka kod Revidiranog simpleks metoda a. Velika brzina izvr{avawa za veliki broj problema u prak-si (i pored velike slo`e-nosti) Nedostaci: a. Slo`enost algoritma nije polinomijalna (Minti i Kli su konstruisali primer na kome Simpleks dosti`e NP slo`enost a. Nedovoqno iskori{}ewe ret-ko}e polazne matrice prob-lema (nemogu}nost primene za probleme ekstremno velike dimenzije) a. Nagomilavawe numeri~ke gre{ke (izbegava se revidiranom Simpleks metodom, koji je mawe stabilan i znatno spo-riji)
 A sad ono {to o~ekujete od samog po~etka predavawa: KRAJ!!! PREZENTACIJA PROGRAMA MARPLEX
A sad ono {to o~ekujete od samog po~etka predavawa: KRAJ!!! PREZENTACIJA PROGRAMA MARPLEX


