LINEAR Q U A T I O N

LINEAR Q U A T I O N S A TUTORIAL Credits START

Menu Standard form Slope/Intercept form Writing Graphing Systems Real-life examples Definitions and formulas Back to title page

Standard Form An linear equation in standard form looks like Ax + By = C, where A, B, and C are integers and A and B do not both equal zero.

The equation below is written in Slope/Intercept Form. Follow the steps to change it into Standard Form. 1. 2. Multiply the entire equation by the LCD. 3. -3 x Find the LCD in order to eliminate the fractions. Now that you have only integers for the coefficients, move the 3 x to the other side of the equation by using inverse operations. 4. Now your equation is in Ax +By = C where A = -3, B = 4, and C = 8.

Now you try! Change the follow equation from Slope/Intercept Form to Standard Form. Click for the answer

Answer 1. Find the LCD in order to eliminate the fractions. 2. Multiply the entire equation by the LCD. -14 x 3. Now that you have only integers for the coefficients, move the 14 x to the other side of the equation by using inverse operations. Now your equation is in Ax +By = C where A = -14, B = 4, and C = 1. Back to Menu

Putting equations into Slope/Intercept form STEPS to isolate y 1. Addition or Subtraction 2. Multiply or Divide 3. Reduce Fractions Examples 1 - 3 Back to Menu

Example 1 12 y + 4 = 8 x -4 -4 subtract 4 12 y = 8 x -4 (12/12)y = (8 /12)x - (4/12) divide by 12 y = (8/12)x - (4/12) reduce fractions y = (2/3)x - (1/3)

Example 2 4 x + (2/7)y = 2 - 4 x -4 x + 2 subtract 4 x (2/7)y = -4 x + 2 multiply by the reciprocal (7/2)(2/7)y = (7/2)(-4 x) + (7/2)(2) y = (-28/2)x + (14/2) reduce y = -14 x + 7

Example 3 2 x + 6 - 3 y = 8 + 5 x - 2 y -6 -6 2 x - 3 y = 2 + 5 x - 2 y + 2 y 2 x - y = 2 + 5 x - 2 x - y = 2 + 3 x (-1/-1)y= (2/-1) + (3/-1)x y = -2 - 3 x or y = -3 x - 2 subtract 6 add 2 y subtract 2 x divide by -1 Back to STEPS

Writing Linear Equations STEPS 1. Find the slope of the line by using the formula or knowing if it is parallel or perpendicular. 2. Substitute m, x, and y into the equation and solve for b. Then rewrite with the known m and b. Or use a point and the slope and substitute those into the point/slope formula. Back to Examples A - C Menu

Example A Write the equation of a line through (4, -6) and (2, 0). m = 0 - (-6) = 6 = -3 2 - 4 -2 0 = -3(2) + b or y - 0 = -3(x - 2) 0 = -6 + b y = -3 x + 6 6=b so, y = -3 x + 6

Example B Write the equation of a line through (-5, 7) and parallel to y = 2 x -(9/2). Old m = 2 New m = 2 because parallel means same slope y - 7 = 2[x- (-5)] y - 7 = 2(x + 5) y - 7 = 2 x + 10 y = 2 x + 17

Example C Write the equation of a line through (-3, -12) and perpendicular to 6 x + 4 y = -8. Find the original slope first 6 x + 4 y = -8 y - (-12) = (2/3)[x - (-3)] -6 x = -6 x y + 12 = (2/3)(x + 3) 4 y = -6 x - 8 y + 12 = (2/3)x + 2 (4/4)y = (-6/4)x - (8/4) y = (2/3)x - 10 y = (-3/2)x -2 Old m = (-3/2) Back to Writing New m = (2/3) because perpendicular slopes are negative reciprocals STEPS

Graphing Linear Equations STEPS 1. Be sure the equation is in Slope/Intercept form. 2. Set up a table. Pick at least three x-values. 3. Plot the coordinates. 4. Draw the line. Don’t forget to label all parts of your graph and place arrows at the ends of your line. Shortcut and Example Back to Menu

Shortcut to Graphing Start at the y-intercept and perform the slope steps, or For our example, start at +2 on the y-axis. Go down 3 since the rise is negative, and go to the right 1 since the run is positive. (m = -3/1) See dotted lines that form right triangles attached to our line.

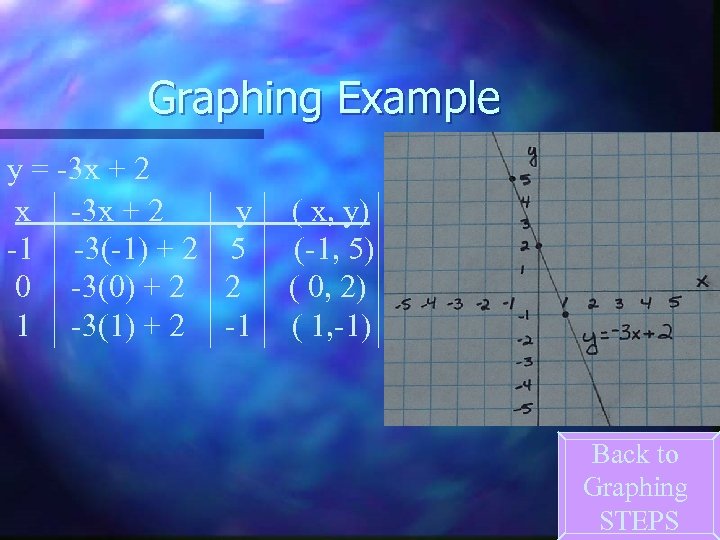Graphing Example y = -3 x + 2 x -3 x + 2 y -1 -3(-1) + 2 5 0 -3(0) + 2 2 1 -3(1) + 2 -1 ( x, y) (-1, 5) ( 0, 2) ( 1, -1) Back to Graphing STEPS

Systems of Linear Equations When two linear equations intersect, that point is called the solution to the system. Choose a method below. Algebraically by Elimination Algebraically by Substitution Graphically Back to Menu

Algebraically by Elimination STEPS 1. Put the equations in Standard Form. Ax + By = C 2. Eliminate the x or y term by making combine to equal zero. (6 y and -6 y) 3. Solve for the remaining term. 4. Substitute The known term into either equation and solve for the other term.

Elimination Example x - 4 y = 12 3 x + 2 y = -34 6 x + 4 y = -68 multiple by 2 & combine 7 x = -56 (7/7)x = (-56/7) Check: -8 -4(-5) = 12 x = -8 -8 +20 =12 -8 -4 y = 12 12 = 12 +8 +8 3(-8) +2(-5) = -34 -4 y = 20 -24 -10 = -34 Back to (-4/-4)y = (20/-4) -34 = -34 System y = -5 Menu

Algebraically by Substitution STEPS 1. Solve either equation for x or y. 2. Substitute the value found into the other equation for that term. 3. Solve for the remaining term. 4. Substitute that value into the second equation used and solve for the other term. 5. Check.

Substitution Example x - 4 y = 12 x = 4 y + 12 3(4 y + 12 ) + 2 y = -34 12 y + 36 + 2 y = -34 14 y + 36 = -34 -36 14 y = -70 (14/14)y = (-70/14) y = -5 x = 4(-5) + 12 x = -20 + 12 x = -8 Check: see elimination example Back to System Menu

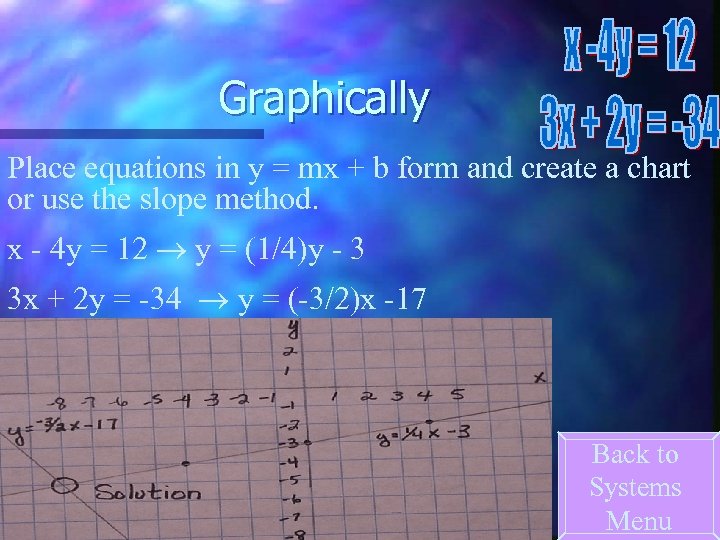Graphically Place equations in y = mx + b form and create a chart or use the slope method. x - 4 y = 12 y = (1/4)y - 3 3 x + 2 y = -34 y = (-3/2)x -17 Back to Systems Menu

Real -life Examples 1. Eleanor uses 10 calories of energy warming up for her morning run. For every minute of running time she uses 15 calories. Write and graph an equation that models the total number of calories (y) that Eleanor uses in warming up and running x minutes. Answer 1

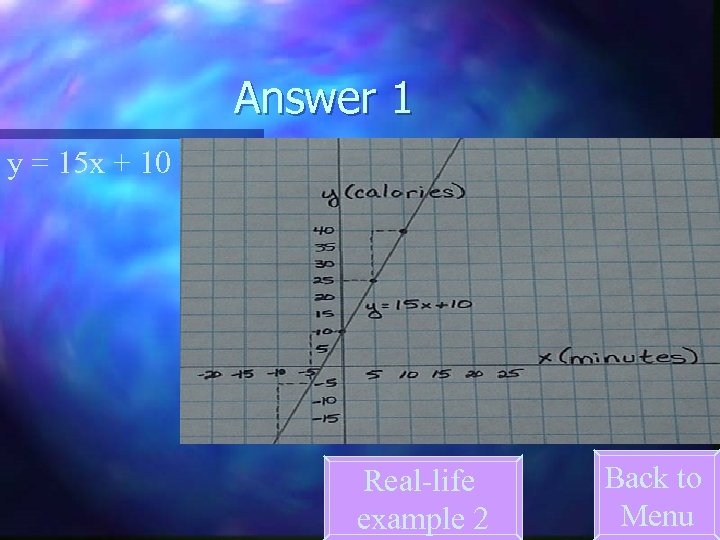Answer 1 y = 15 x + 10 Real-life example 2 Back to Menu

2. A plane travels 300 miles per hour. After 3 hours the plane has traveled 900 miles. If we use the formula D = r * t, where D is distance, r is rate, and t is time, write an equation that will predict how many miles the plane has traveled in 7 hours. Answer 2

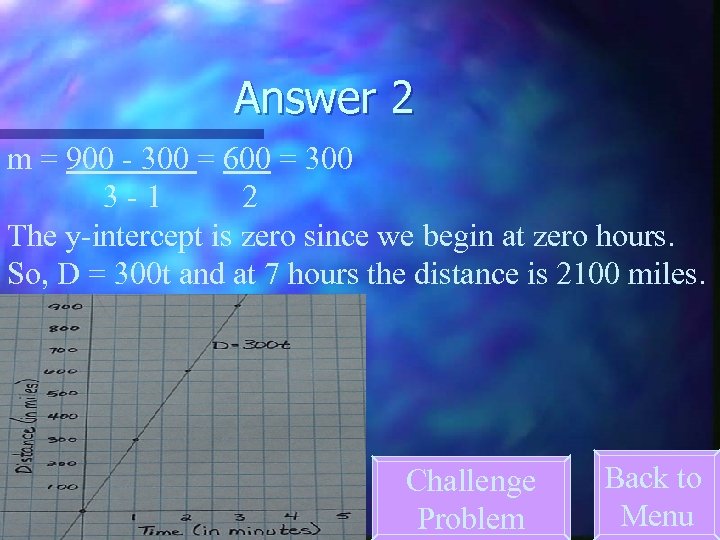Answer 2 m = 900 - 300 = 600 = 300 3 -1 2 The y-intercept is zero since we begin at zero hours. So, D = 300 t and at 7 hours the distance is 2100 miles. Challenge Problem Back to Menu

Gumballs Galore! It is a little known fact, but I’ve heard it said that Tweedledum and Tweedledee, those two jolly fellows that appear in the timeless tale Alice In Wonderland, were fanatics for chewing gum. Yes, indeed. And not just any kind of chewing gum, but the gum that comes in those spherical selling devices found all over the place: gumballs.

One day when these two chaps were downtown shopping, Tweedledee ambled over to a particular enticing gumball machine, while his brother shuffled off in a different direction. Promptly he got out his money purse and began putting his coins in the machine, buying gumball after gumball.

Eventually, Tweedledum caught sight of what was going on, so he scurried right over to the machine. He took out his money bag and began buying some gumballs as well. Being the congenial fellows they were, they did take turns from that point on. First, Tweedledum, then Tweedledee. And so on until all the gumballs were removed from the machine.

Later on at home they counted their treasures and found that the machine had contained a grand total of fifty-five gumballs. Then Tweedledee exclaimed, “Gee, thirteen times your number exceeds eight times my number by one. ” Tweedledum snorted, “But of course, you still have more than I. You found the machine before I arrived. ”

“Sorry, brother, ” responded the former. “Better luck next time!” How many more delicious gumballs did Tweedledee buy than his less fortunate brother? Be sure to define your variable(s) used and write each step out. Click for answer

Answer to Challenge Problem Total gumballs = 55 Let x = Tweedledee’s number of gumballs (34) Let y = Tweedledum’s number of gumballs (21) x + y = 55 and 13 y = 8 x +1 Substitution method y = 55 - x -8 x + 13(55 - x) = 1 x = 34 -8 x + 715 - 13 x = 1 y = 21 -21 x = -714

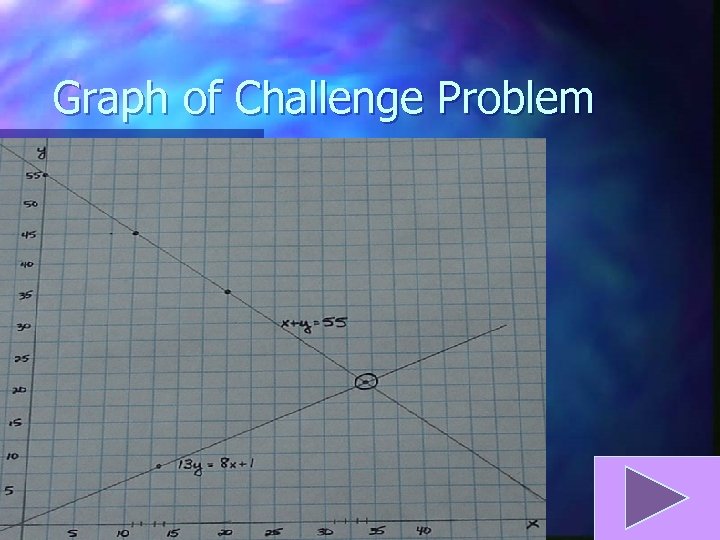Graph of Challenge Problem

If this is not the same as your answer, Please try again. If this is the same as your answer, Back to Menu

Definitions and formulas Line Slope No Slope/Intercept form Parallel Undefined slope Perpendicular x-intercept Point/Slope y-intercept Standard Form Back to Menu

Line A line is a set of collinear points that extend infinitely in both directions.

No Slope No slope or zero slope is a horizontal line with an equation of y = b, where b is the y coordinate of all of the points.

Parallel lines maintain the same distance apart infinitely so they have the same slope.

Perpendicular lines intersect and form four 90° angles at the point of intersection. Their slopes are negative reciprocals of each other. Ex. 1/2 and -2/1 4/3 and -3/4

Point/Slope Form y - y = m( x - x ) 1 1 One point needs to be substituted in for x and y. The slope needs to be substituted in for m. 1 1

Slope is the ratio of the differences of the y-values to the difference of the corresponding x-values, where x 1 x 2.

Slope/Intercept Form Slope/Intercept form of a linear equation is y = mx + b, where m is the slope of the line and b is the y-intercept of the line.

Undefined Slope An undefined slope is where x 1 = x 2 and m = a number/0. (illegal) It is a vertical line with the equation x = a, where a is the x-coordinate of all of the points.

x-intercept The x-intercept is where the line crosses the x-axis.

y-intercept The y-intercept is the point where the line crosses the y-axis.

Standard Form is Ax + By = C, where A and B are integers and both cannot be zero. Ex: 4 x +6 y = 54

Credits This tutorial was created by Kathaleen Bitter. Pictured with daughters Cassandra & Samantha. EDI 581 Spring 2002 E-mail your comments to kbit 1215@brockport. edu www. icq. com/friendship/applause. html www. hud. gov/kids/ahhhl. html www. dutchindoorvillage. com/diswonderland. html www. nursing. purdue. edu/ce/Default. htm www. redheads. com. au/Cash%20 In%20 Webpage/cash_in. htm www. transabroad. com/listings/travel/index. shtml “How Do I Feel” (The Burrito Song) By Hoku www. state. il. us/dfi/ www. utexas. edu/…/msl-diagnostic/4 -stats. html www. candymachines. com/newbanks. htm www. algebra. com/algebra/lessons/graphing/ Back to Menu