d263c40e4a39ce70b800ce508e69be20.ppt
- Количество слайдов: 120
 LINEAR PROGRAMMING SOLUTION TECHNIQUES: GRAPHICAL AND COMPUTER METHODS
LINEAR PROGRAMMING SOLUTION TECHNIQUES: GRAPHICAL AND COMPUTER METHODS
 LEARNING OBJECTIVES Ø Understand basic assumptions and properties of linear programming (LP). Ø Use graphical solution procedures for LP problems with only two variables to understand how LP problems are solved. Ø Understand special situations such as redundancy, infeasibility, unboundedness, and alternate optimal solutions in LP problems. Ø Understand how to set up LP problems on a spreadsheet and solve them using Excel’s solver.
LEARNING OBJECTIVES Ø Understand basic assumptions and properties of linear programming (LP). Ø Use graphical solution procedures for LP problems with only two variables to understand how LP problems are solved. Ø Understand special situations such as redundancy, infeasibility, unboundedness, and alternate optimal solutions in LP problems. Ø Understand how to set up LP problems on a spreadsheet and solve them using Excel’s solver.
 INTRODUCTION Ø Management decisions in many organizations involve trying to make most effective use of resources (machinery, labor, money, time, warehouse space, and raw materials) in order to: ØProduce products - such as computers, automobiles, or clothing or ØProvide services - such as package delivery, health services, or investment decisions. Ø To solve problems of resource allocation one may use mathematical programming.
INTRODUCTION Ø Management decisions in many organizations involve trying to make most effective use of resources (machinery, labor, money, time, warehouse space, and raw materials) in order to: ØProduce products - such as computers, automobiles, or clothing or ØProvide services - such as package delivery, health services, or investment decisions. Ø To solve problems of resource allocation one may use mathematical programming.
 LINEAR PROGRAMMING ØLinear programming (LP) is the most common type of mathematical programming. ØLP seeks to maximize or minimize a linear objective function subject to a set of linear constraints ØLP assumes all relevant input data and parameters are known with certainty (deterministic models). ØComputers play an important role in the solution of LP problems
LINEAR PROGRAMMING ØLinear programming (LP) is the most common type of mathematical programming. ØLP seeks to maximize or minimize a linear objective function subject to a set of linear constraints ØLP assumes all relevant input data and parameters are known with certainty (deterministic models). ØComputers play an important role in the solution of LP problems
 LP MODEL COMPONENTS AND FORMULATION § Decision variables - mathematical symbols representing levels of activity of a firm. § Objective function - a linear mathematical relationship describing an objective of the firm, in terms of decision variables, that is to be maximized or minimized § Constraints - restrictions placed on the firm by the operating environment stated in linear relationships of the decision variables. § Parameters - numerical coefficients and constants used in the objective function and constraint equations.
LP MODEL COMPONENTS AND FORMULATION § Decision variables - mathematical symbols representing levels of activity of a firm. § Objective function - a linear mathematical relationship describing an objective of the firm, in terms of decision variables, that is to be maximized or minimized § Constraints - restrictions placed on the firm by the operating environment stated in linear relationships of the decision variables. § Parameters - numerical coefficients and constants used in the objective function and constraint equations.
 DEVELOPMENT OF A LP MODEL Ø LP applied extensively to problems areas Ø medical, transportation, operations, Ø financial, marketing, accounting, Ø human resources, and agriculture. Ø Development and solution of all LP models can be examined in a four step process: (1) identification of the problem as solvable by LP (2) formulation of the mathematical model. (3) solution. (4) interpretation.
DEVELOPMENT OF A LP MODEL Ø LP applied extensively to problems areas Ø medical, transportation, operations, Ø financial, marketing, accounting, Ø human resources, and agriculture. Ø Development and solution of all LP models can be examined in a four step process: (1) identification of the problem as solvable by LP (2) formulation of the mathematical model. (3) solution. (4) interpretation.
 BASIC STEPS OF DEVELOPING A LP MODEL Formulation – Process of translating problem scenario into simple LP model framework with a set of mathematical relationships. Solution – Mathematical relationships resulting from formulation process are solved to identify optimal solution. Interpretation and What-if Analysis – Problem solver or analyst works with the manager to § interpret results and implications of problem solution. § investigate changes in input parameters and model variables and impact on problem solution results.
BASIC STEPS OF DEVELOPING A LP MODEL Formulation – Process of translating problem scenario into simple LP model framework with a set of mathematical relationships. Solution – Mathematical relationships resulting from formulation process are solved to identify optimal solution. Interpretation and What-if Analysis – Problem solver or analyst works with the manager to § interpret results and implications of problem solution. § investigate changes in input parameters and model variables and impact on problem solution results.
 LINEAR EQUATIONS AND INEQUALITIES § This is a linear equation: 2 A + 5 B = 10 § This equation is not linear: 2 A 2 + 5 B 3 + 3 AB = 10 § LP uses, in many cases, inequalities like: A + B C or A + B C
LINEAR EQUATIONS AND INEQUALITIES § This is a linear equation: 2 A + 5 B = 10 § This equation is not linear: 2 A 2 + 5 B 3 + 3 AB = 10 § LP uses, in many cases, inequalities like: A + B C or A + B C
 BASIC ASSUMPTIONS OF A LP MODEL 1. Conditions of certainty exist. 2. Proportionality in objective function and constraints (1 unit – 3 hours, 3 units- 9 hours). 3. Additivity (total of all activities equals sum of individual activities). 4. Divisibility assumption that solutions need not necessarily be in whole numbers (integers); ie. decision variables can take on any fractional value.
BASIC ASSUMPTIONS OF A LP MODEL 1. Conditions of certainty exist. 2. Proportionality in objective function and constraints (1 unit – 3 hours, 3 units- 9 hours). 3. Additivity (total of all activities equals sum of individual activities). 4. Divisibility assumption that solutions need not necessarily be in whole numbers (integers); ie. decision variables can take on any fractional value.
 FORMULATING A LP PROBLEM § A common LP application is product mix problem. – Two or more products are usually produced using limited resources - such as personnel, machines, raw materials, and so on. § Profit firm seeks to maximize is based on profit contribution per unit of each product. § Firm would like to determine – How many units of each product it should produce in order to maximize overall profit given its limited resources.
FORMULATING A LP PROBLEM § A common LP application is product mix problem. – Two or more products are usually produced using limited resources - such as personnel, machines, raw materials, and so on. § Profit firm seeks to maximize is based on profit contribution per unit of each product. § Firm would like to determine – How many units of each product it should produce in order to maximize overall profit given its limited resources.
 MAXIMIZATION MODEL EXAMPLES: § § § BEAVER CREEK EXAMPLE FLAIR FURNITURE EXAMPLE GALAXY INDUSTRIES EXAMPLE
MAXIMIZATION MODEL EXAMPLES: § § § BEAVER CREEK EXAMPLE FLAIR FURNITURE EXAMPLE GALAXY INDUSTRIES EXAMPLE
 PROBLEM DEFINITION: BEAVER CREEK MAXIMIZATION PROBLEM (1 of 18) § Product mix problem - Beaver Creek Pottery Company § How many bowls and mugs should be produced to maximize profits given labor and materials constraints? § Product resource requirements and unit profit:
PROBLEM DEFINITION: BEAVER CREEK MAXIMIZATION PROBLEM (1 of 18) § Product mix problem - Beaver Creek Pottery Company § How many bowls and mugs should be produced to maximize profits given labor and materials constraints? § Product resource requirements and unit profit:
 PROBLEM DEFINITION: BEAVER CREEK EXAMPLE (2 of 18) Resource Availability: 40 hrs of labor per day 120 lbs of clay Decision Variables x 1 = number of bowls to produce per day x 2 = number of mugs to produce per day Objective Function: Maximize Z = $40 x 1 + $50 x 2 Where Z = profit per day Resource Constraints: 1 x 1 + 2 x 2 40 hours of labor 4 x 1 + 3 x 2 120 pounds of clay Non-Negativity Constraints: x 1 0; x 2 0
PROBLEM DEFINITION: BEAVER CREEK EXAMPLE (2 of 18) Resource Availability: 40 hrs of labor per day 120 lbs of clay Decision Variables x 1 = number of bowls to produce per day x 2 = number of mugs to produce per day Objective Function: Maximize Z = $40 x 1 + $50 x 2 Where Z = profit per day Resource Constraints: 1 x 1 + 2 x 2 40 hours of labor 4 x 1 + 3 x 2 120 pounds of clay Non-Negativity Constraints: x 1 0; x 2 0
 PROBLEM DEFINITION: BEAVER CREEK EXAMPLE (3 of 18) Complete Linear Programming Model: Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0
PROBLEM DEFINITION: BEAVER CREEK EXAMPLE (3 of 18) Complete Linear Programming Model: Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0
 FEASIBLE SOLUTIONS: BEAVER CREEK EXAMPLE (4 of 18) A feasible solution does not violate any of the constraints: Example x 1 = 5 bowls x 2 = 10 mugs Z = $40 x 1 + $50 x 2 = $700 Labor constraint check: 1(5) + 2(10) = 25 < 40 hours, within constraint Clay constraint check: 4(5) + 3(10) = 50 < 120 pounds, within constraint
FEASIBLE SOLUTIONS: BEAVER CREEK EXAMPLE (4 of 18) A feasible solution does not violate any of the constraints: Example x 1 = 5 bowls x 2 = 10 mugs Z = $40 x 1 + $50 x 2 = $700 Labor constraint check: 1(5) + 2(10) = 25 < 40 hours, within constraint Clay constraint check: 4(5) + 3(10) = 50 < 120 pounds, within constraint
 INFEASIBLE SOLUTIONS: BEAVER CREEK EXAMPLE (5 of 18) An infeasible solution violates at least one of the constraints: Example x 1 = 10 bowls x 2 = 20 mugs Z = $1400 Labor constraint check: 1(10) + 2(20) = 50 > 40 hours, violates the constraint
INFEASIBLE SOLUTIONS: BEAVER CREEK EXAMPLE (5 of 18) An infeasible solution violates at least one of the constraints: Example x 1 = 10 bowls x 2 = 20 mugs Z = $1400 Labor constraint check: 1(10) + 2(20) = 50 > 40 hours, violates the constraint
 The set of all points that satisfy all the constraints of the model is called a FEASIBLE REGION
The set of all points that satisfy all the constraints of the model is called a FEASIBLE REGION
 GRAPHICAL SOLUTION OF LINEAR PROGRAMMING MODELS Ø Graphical solution is limited to linear programming models containing only two decision variables (can be used with three variables but only with great difficulty). Ø Graphical methods provide visualization of how a solution for a linear programming problem is obtained.
GRAPHICAL SOLUTION OF LINEAR PROGRAMMING MODELS Ø Graphical solution is limited to linear programming models containing only two decision variables (can be used with three variables but only with great difficulty). Ø Graphical methods provide visualization of how a solution for a linear programming problem is obtained.
 Ø Primary advantage of two-variable LP models (such as Beaver Creek problem) is their solution can be graphically illustrated using two-dimensional graph. Ø Allows one to provide an intuitive explanation of how more complex solution procedures work for larger LP models.
Ø Primary advantage of two-variable LP models (such as Beaver Creek problem) is their solution can be graphically illustrated using two-dimensional graph. Ø Allows one to provide an intuitive explanation of how more complex solution procedures work for larger LP models.
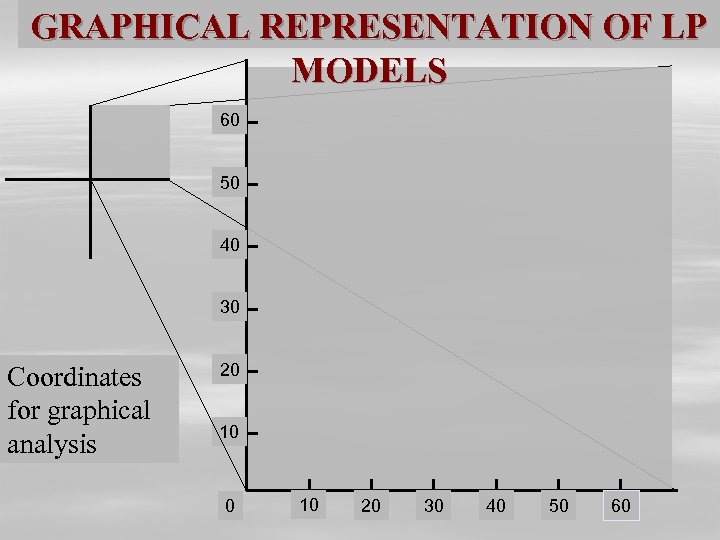 GRAPHICAL REPRESENTATION OF LP MODELS 60 50 40 30 Coordinates for graphical analysis 20 10 20 30 40 50 60
GRAPHICAL REPRESENTATION OF LP MODELS 60 50 40 30 Coordinates for graphical analysis 20 10 20 30 40 50 60
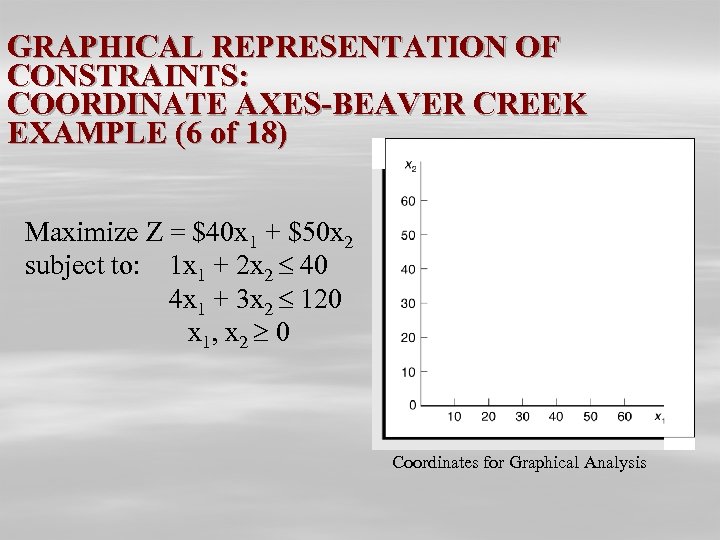 GRAPHICAL REPRESENTATION OF CONSTRAINTS: COORDINATE AXES-BEAVER CREEK EXAMPLE (6 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Coordinates for Graphical Analysis
GRAPHICAL REPRESENTATION OF CONSTRAINTS: COORDINATE AXES-BEAVER CREEK EXAMPLE (6 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Coordinates for Graphical Analysis
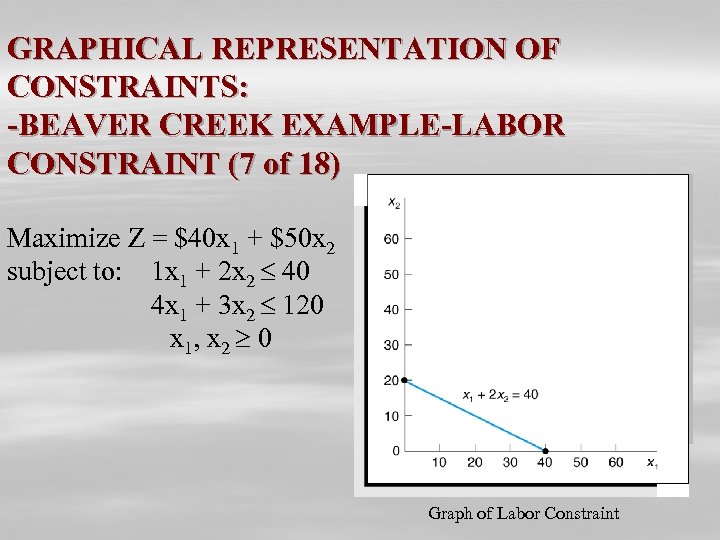 GRAPHICAL REPRESENTATION OF CONSTRAINTS: -BEAVER CREEK EXAMPLE-LABOR CONSTRAINT (7 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Graph of Labor Constraint
GRAPHICAL REPRESENTATION OF CONSTRAINTS: -BEAVER CREEK EXAMPLE-LABOR CONSTRAINT (7 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Graph of Labor Constraint
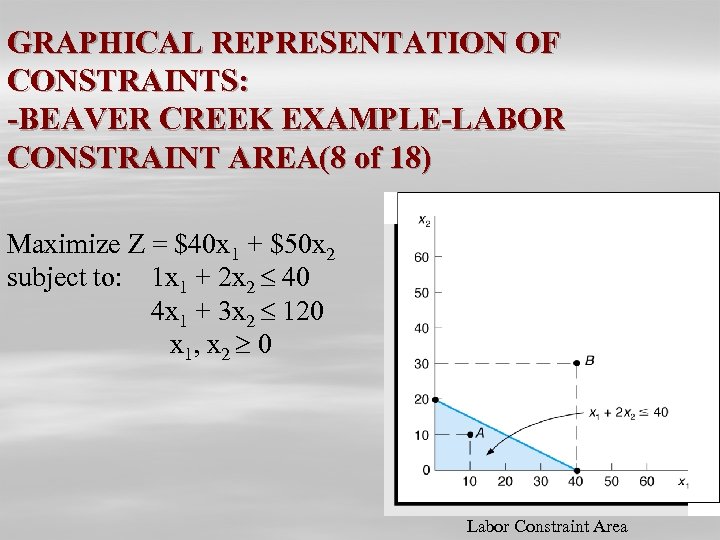 GRAPHICAL REPRESENTATION OF CONSTRAINTS: -BEAVER CREEK EXAMPLE-LABOR CONSTRAINT AREA(8 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Labor Constraint Area
GRAPHICAL REPRESENTATION OF CONSTRAINTS: -BEAVER CREEK EXAMPLE-LABOR CONSTRAINT AREA(8 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Labor Constraint Area
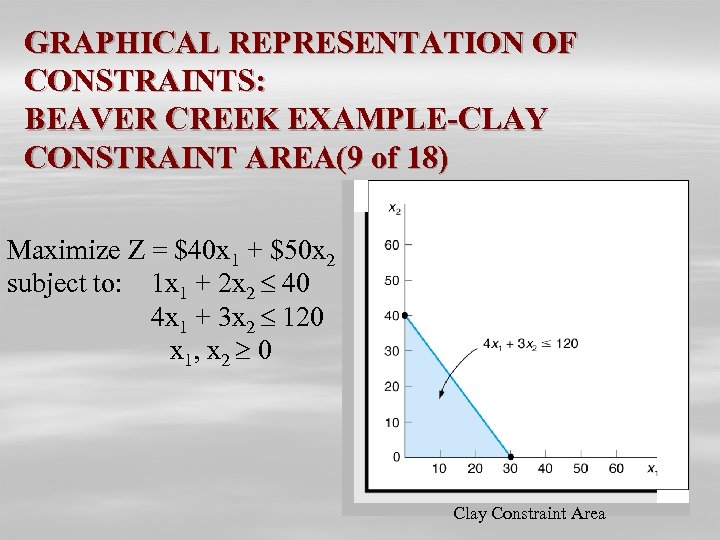 GRAPHICAL REPRESENTATION OF CONSTRAINTS: BEAVER CREEK EXAMPLE-CLAY CONSTRAINT AREA(9 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Clay Constraint Area
GRAPHICAL REPRESENTATION OF CONSTRAINTS: BEAVER CREEK EXAMPLE-CLAY CONSTRAINT AREA(9 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Clay Constraint Area
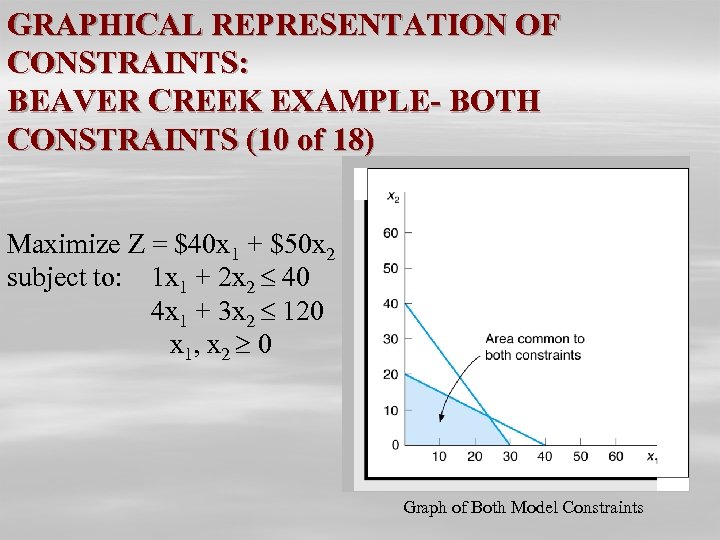 GRAPHICAL REPRESENTATION OF CONSTRAINTS: BEAVER CREEK EXAMPLE- BOTH CONSTRAINTS (10 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Graph of Both Model Constraints
GRAPHICAL REPRESENTATION OF CONSTRAINTS: BEAVER CREEK EXAMPLE- BOTH CONSTRAINTS (10 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Graph of Both Model Constraints
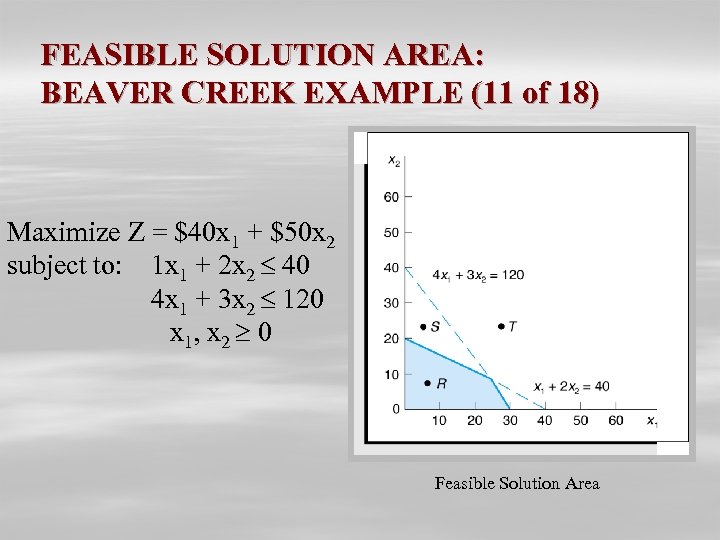 FEASIBLE SOLUTION AREA: BEAVER CREEK EXAMPLE (11 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Feasible Solution Area
FEASIBLE SOLUTION AREA: BEAVER CREEK EXAMPLE (11 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Feasible Solution Area
 GRAPHICAL SOLUTION: ISOPROFIT LINE SOLUTION METHOD Ø Optimal solution is the point in feasible region that produces highest profit Ø There are many possible solution points in region. Ø How do we go about selecting the best one, one yielding highest profit? Ø Let objective function (that is, $$40 x 1 + $50 x 2) guide one towards optimal point in feasible region. Ø Plot line representing objective function on graph as a straight line.
GRAPHICAL SOLUTION: ISOPROFIT LINE SOLUTION METHOD Ø Optimal solution is the point in feasible region that produces highest profit Ø There are many possible solution points in region. Ø How do we go about selecting the best one, one yielding highest profit? Ø Let objective function (that is, $$40 x 1 + $50 x 2) guide one towards optimal point in feasible region. Ø Plot line representing objective function on graph as a straight line.
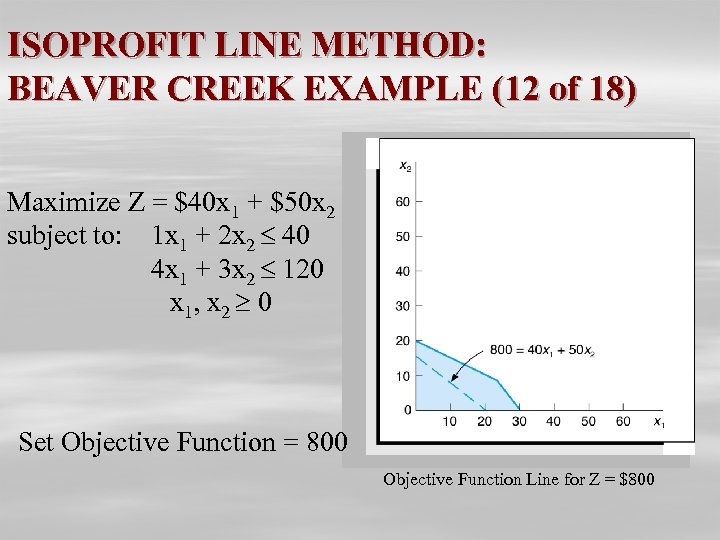 ISOPROFIT LINE METHOD: BEAVER CREEK EXAMPLE (12 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Set Objective Function = 800 Objective Function Line for Z = $800
ISOPROFIT LINE METHOD: BEAVER CREEK EXAMPLE (12 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Set Objective Function = 800 Objective Function Line for Z = $800
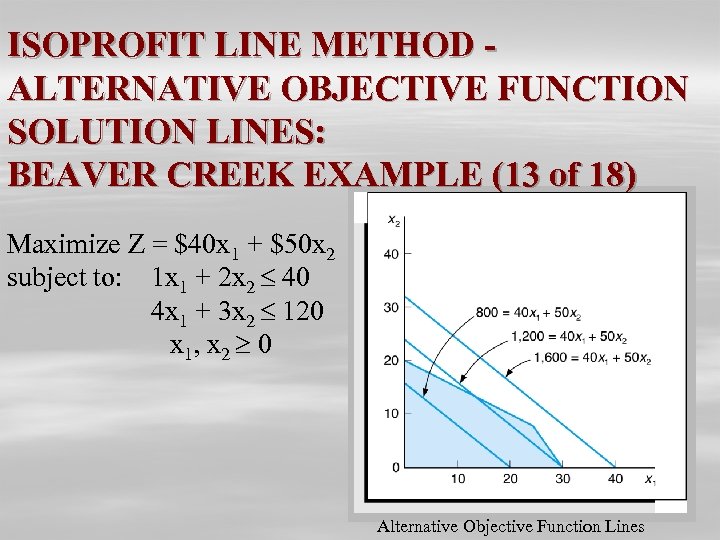 ISOPROFIT LINE METHOD ALTERNATIVE OBJECTIVE FUNCTION SOLUTION LINES: BEAVER CREEK EXAMPLE (13 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Alternative Objective Function Lines
ISOPROFIT LINE METHOD ALTERNATIVE OBJECTIVE FUNCTION SOLUTION LINES: BEAVER CREEK EXAMPLE (13 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Alternative Objective Function Lines
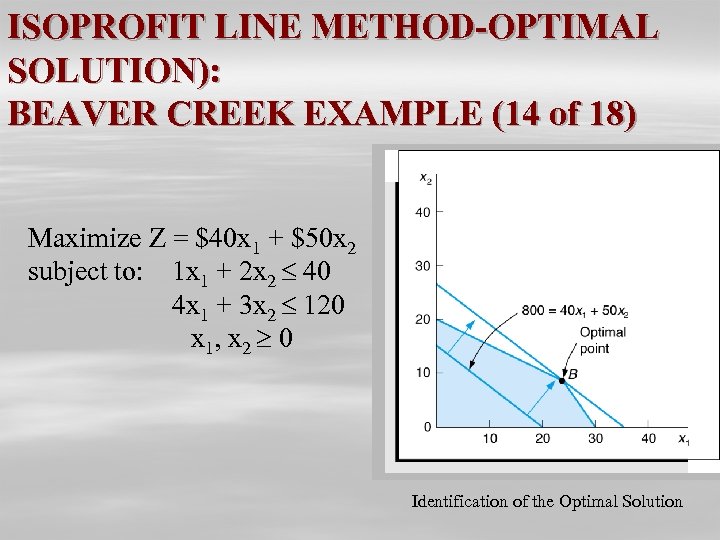 ISOPROFIT LINE METHOD-OPTIMAL SOLUTION): BEAVER CREEK EXAMPLE (14 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Identification of the Optimal Solution
ISOPROFIT LINE METHOD-OPTIMAL SOLUTION): BEAVER CREEK EXAMPLE (14 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Identification of the Optimal Solution
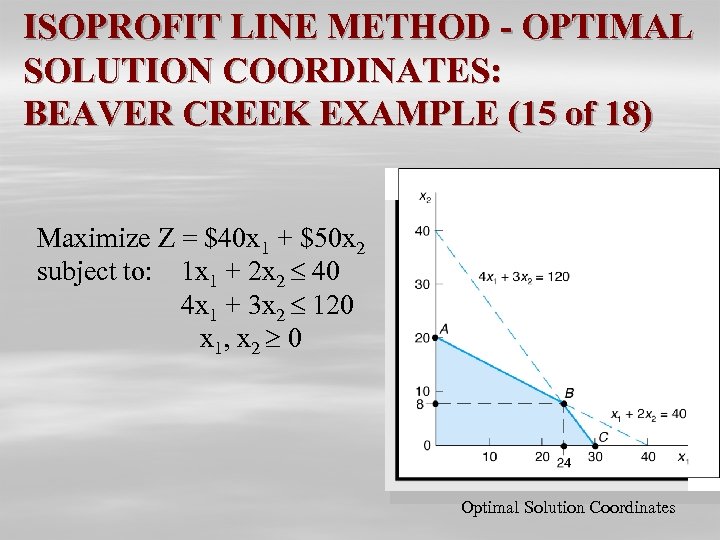 ISOPROFIT LINE METHOD - OPTIMAL SOLUTION COORDINATES: BEAVER CREEK EXAMPLE (15 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Optimal Solution Coordinates
ISOPROFIT LINE METHOD - OPTIMAL SOLUTION COORDINATES: BEAVER CREEK EXAMPLE (15 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Optimal Solution Coordinates
 CORNER POINT PROPERTY It is a very important property of Linear Programming problems: This property states optimal solution to LP problem will always occur at a corner point.
CORNER POINT PROPERTY It is a very important property of Linear Programming problems: This property states optimal solution to LP problem will always occur at a corner point.
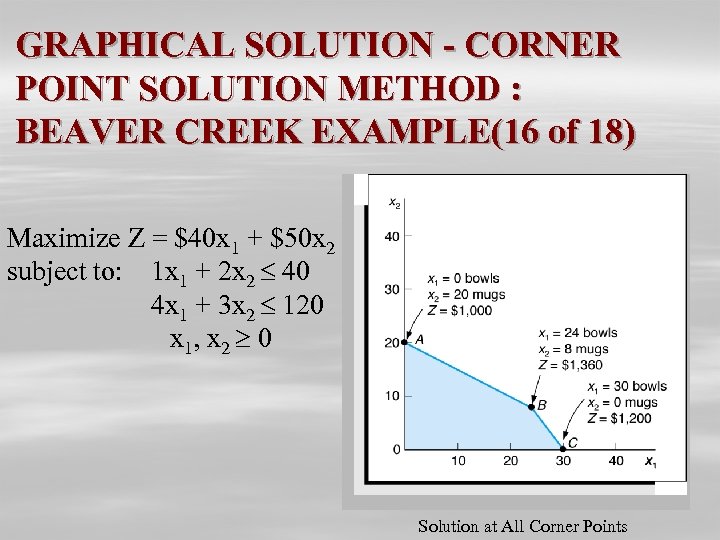 GRAPHICAL SOLUTION - CORNER POINT SOLUTION METHOD : BEAVER CREEK EXAMPLE(16 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Solution at All Corner Points
GRAPHICAL SOLUTION - CORNER POINT SOLUTION METHOD : BEAVER CREEK EXAMPLE(16 of 18) Maximize Z = $40 x 1 + $50 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Solution at All Corner Points
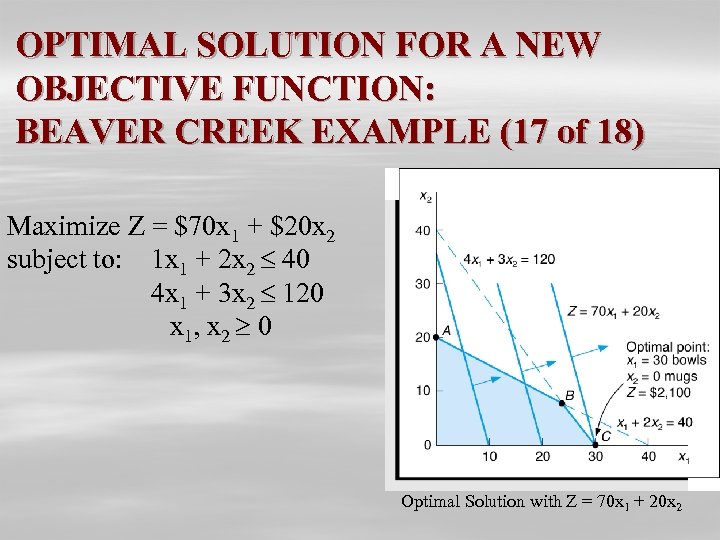 OPTIMAL SOLUTION FOR A NEW OBJECTIVE FUNCTION: BEAVER CREEK EXAMPLE (17 of 18) Maximize Z = $70 x 1 + $20 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Optimal Solution with Z = 70 x 1 + 20 x 2
OPTIMAL SOLUTION FOR A NEW OBJECTIVE FUNCTION: BEAVER CREEK EXAMPLE (17 of 18) Maximize Z = $70 x 1 + $20 x 2 subject to: 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1, x 2 0 Optimal Solution with Z = 70 x 1 + 20 x 2
 SLACK VARIABLES Ø Standard form requires that all constraints be in the form of equations. Ø A slack variable is added to a constraint to convert it to an equation (=). Ø A slack variable represents unused resources. Ø A slack variable contributes nothing to the objective function value.
SLACK VARIABLES Ø Standard form requires that all constraints be in the form of equations. Ø A slack variable is added to a constraint to convert it to an equation (=). Ø A slack variable represents unused resources. Ø A slack variable contributes nothing to the objective function value.
 STANDARD FORM OF LINEAR PROGRAMMING MODEL: BEAVER CREEK EXAMPLE (18 of 18) Max Z = 40 x 1 + 50 x 2 + s 1 +s 2 subject to: 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 x 1, x 2, s 1, s 2 0 Where: x 1 = number of bowls x 2 = number of mugs s 1, s 2 are slack variables Solution Points A, B, and C with Slack
STANDARD FORM OF LINEAR PROGRAMMING MODEL: BEAVER CREEK EXAMPLE (18 of 18) Max Z = 40 x 1 + 50 x 2 + s 1 +s 2 subject to: 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 x 1, x 2, s 1, s 2 0 Where: x 1 = number of bowls x 2 = number of mugs s 1, s 2 are slack variables Solution Points A, B, and C with Slack
 PROBLEM DEFINITION: FLAIR FURNITURE MAXIMIZATION EXAMPLE (1 of 19) Company Data and Constraints - Ø Flair Furniture Company produces tables and chairs. Ø Each table requires: 4 hours of carpentry and 2 hours of painting. Ø Each chair requires: 3 hours of carpentry and 1 hour of painting. Ø Available production capacity: 240 hours of carpentry time and 100 hours of painting time. Ø Due to existing inventory of chairs, Flair is to make no more than 60 new chairs. Ø Each table sold results in $7 profit, while each chair produced yields $5 profit. Flair Furniture’s problem: Ø Determine the best possible combination of tables and chairs to manufacture in order to attain maximum profit.
PROBLEM DEFINITION: FLAIR FURNITURE MAXIMIZATION EXAMPLE (1 of 19) Company Data and Constraints - Ø Flair Furniture Company produces tables and chairs. Ø Each table requires: 4 hours of carpentry and 2 hours of painting. Ø Each chair requires: 3 hours of carpentry and 1 hour of painting. Ø Available production capacity: 240 hours of carpentry time and 100 hours of painting time. Ø Due to existing inventory of chairs, Flair is to make no more than 60 new chairs. Ø Each table sold results in $7 profit, while each chair produced yields $5 profit. Flair Furniture’s problem: Ø Determine the best possible combination of tables and chairs to manufacture in order to attain maximum profit.
 DECISION VARIABLES: FLAIR FURNITURE EXAMPLE (2 of 19) Ø Problem facing Flair is to determine how many chairs and tables to produce to yield maximum profit? Ø In Flair Furniture problem, there are two unknown entities: Ø T- number of tables to be produced. Ø C- number of chairs to be produced.
DECISION VARIABLES: FLAIR FURNITURE EXAMPLE (2 of 19) Ø Problem facing Flair is to determine how many chairs and tables to produce to yield maximum profit? Ø In Flair Furniture problem, there are two unknown entities: Ø T- number of tables to be produced. Ø C- number of chairs to be produced.
 OBJECTIVE FUNCTION: FLAIR FURNITURE EXAMPLE (3 of 19) Ø Objective function states the goal of problem. ØWhat major objective is to be solved? ØMaximize profit! Ø An LP model must have a single objective function. In Flair’s problem, total profit may be expressed as: Using decision variables T and C - Maximize $7 T + $5 C ($7 profit per table) x (number of tables produced) + ($5 profit per chair) x (number of chairs produced)
OBJECTIVE FUNCTION: FLAIR FURNITURE EXAMPLE (3 of 19) Ø Objective function states the goal of problem. ØWhat major objective is to be solved? ØMaximize profit! Ø An LP model must have a single objective function. In Flair’s problem, total profit may be expressed as: Using decision variables T and C - Maximize $7 T + $5 C ($7 profit per table) x (number of tables produced) + ($5 profit per chair) x (number of chairs produced)
 CONSTRAINTS: FLAIR FURNITURE EXAMPLE (4 of 19) Ø Denote conditions that prevent one from selecting any specific subjective value for decision variables. Ø In Flair Furniture’s problem, there are three restrictions on solution. ØRestrictions 1 and 2 have to do with available carpentry and painting times, respectively. ØRestriction 3 is concerned with upper limit on the number of chairs.
CONSTRAINTS: FLAIR FURNITURE EXAMPLE (4 of 19) Ø Denote conditions that prevent one from selecting any specific subjective value for decision variables. Ø In Flair Furniture’s problem, there are three restrictions on solution. ØRestrictions 1 and 2 have to do with available carpentry and painting times, respectively. ØRestriction 3 is concerned with upper limit on the number of chairs.
 CONSTRAINTS: FLAIR FURNITURE EXAMPLE (5 of 19) Ø There are 240 carpentry hours available. Ø 4 T + 3 C < 240 Ø There are 100 painting hours available. Ø 2 T + 1 C 100 Ø The marketing specified chairs limit constraint. Ø C 60 Ø The non-negativity constraints. Ø T 0 (number of tables produced is 0) Ø C 0 (number of chairs produced is 0)
CONSTRAINTS: FLAIR FURNITURE EXAMPLE (5 of 19) Ø There are 240 carpentry hours available. Ø 4 T + 3 C < 240 Ø There are 100 painting hours available. Ø 2 T + 1 C 100 Ø The marketing specified chairs limit constraint. Ø C 60 Ø The non-negativity constraints. Ø T 0 (number of tables produced is 0) Ø C 0 (number of chairs produced is 0)
 BUILDING THE COMPLETE MATHEMATICAL MODEL: FLAIR FURNITURE EXAMPLE (6 of 19) Maximize profit = $7 T + $5 C (objective function) Subject to constraints 4 T + 3 C 240 (carpentry constraint) 2 T + 1 C 100 (painting constraint) C 60 (chairs limit constraint) T 0 (non-negativity constraint on tables) C 0 (non-negativity constraint on chairs)
BUILDING THE COMPLETE MATHEMATICAL MODEL: FLAIR FURNITURE EXAMPLE (6 of 19) Maximize profit = $7 T + $5 C (objective function) Subject to constraints 4 T + 3 C 240 (carpentry constraint) 2 T + 1 C 100 (painting constraint) C 60 (chairs limit constraint) T 0 (non-negativity constraint on tables) C 0 (non-negativity constraint on chairs)
 CONVERTING INEQUALITIES INTO EQUALITIES BY USING SLACK: FLAIR FURNITURE EXAMPLE (7 of 19) Maximize profit = $7 T + $5 C + 0 s 1 + 0 s 2 + 0 s 3 Subject to constraints 4 T + 3 C + s 1 = 240 (carpentry constraint) 2 T + 1 C + s 2 = 100 (painting constraint) C + s 3 = 60 (chairs limit constraint) T 0 (non-negativity constraint on tables) C 0 (non-negativity constraint on chairs) s 1 s 2 s 3 0 (non-negativity constraints on slacks)
CONVERTING INEQUALITIES INTO EQUALITIES BY USING SLACK: FLAIR FURNITURE EXAMPLE (7 of 19) Maximize profit = $7 T + $5 C + 0 s 1 + 0 s 2 + 0 s 3 Subject to constraints 4 T + 3 C + s 1 = 240 (carpentry constraint) 2 T + 1 C + s 2 = 100 (painting constraint) C + s 3 = 60 (chairs limit constraint) T 0 (non-negativity constraint on tables) C 0 (non-negativity constraint on chairs) s 1 s 2 s 3 0 (non-negativity constraints on slacks)
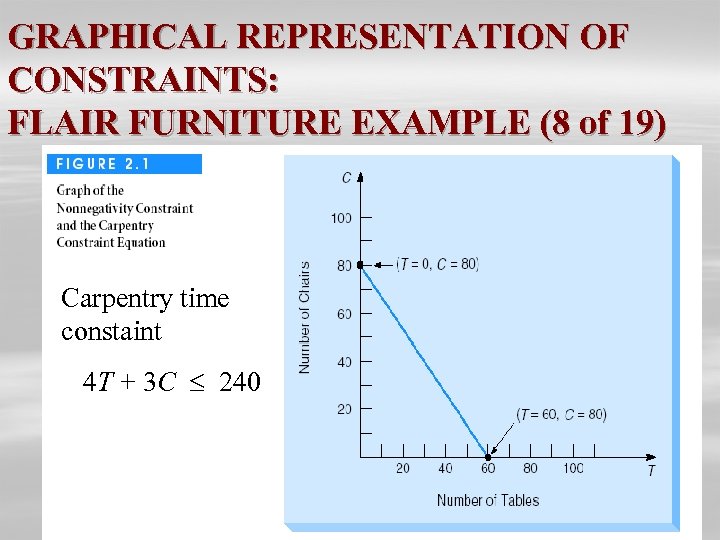 GRAPHICAL REPRESENTATION OF CONSTRAINTS: FLAIR FURNITURE EXAMPLE (8 of 19) Carpentry time constaint 4 T + 3 C 240
GRAPHICAL REPRESENTATION OF CONSTRAINTS: FLAIR FURNITURE EXAMPLE (8 of 19) Carpentry time constaint 4 T + 3 C 240
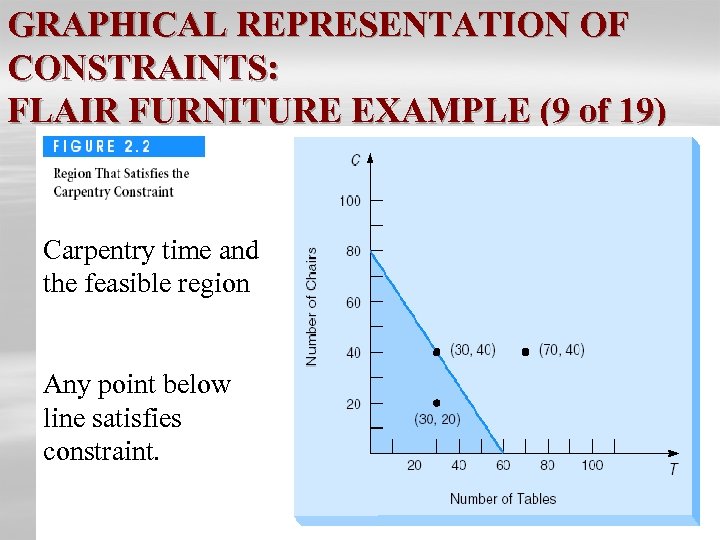 GRAPHICAL REPRESENTATION OF CONSTRAINTS: FLAIR FURNITURE EXAMPLE (9 of 19) Carpentry Time Carpentry time and Constraint the feasible region ) (feasible area Any point below line satisfies constraint.
GRAPHICAL REPRESENTATION OF CONSTRAINTS: FLAIR FURNITURE EXAMPLE (9 of 19) Carpentry Time Carpentry time and Constraint the feasible region ) (feasible area Any point below line satisfies constraint.
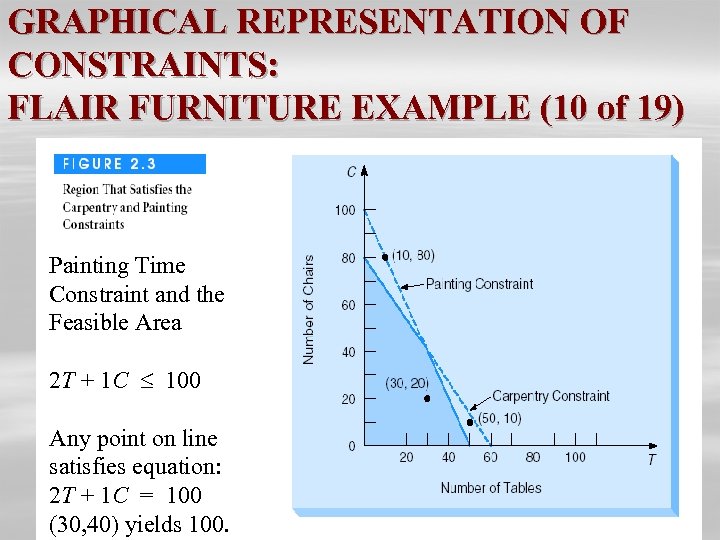 GRAPHICAL REPRESENTATION OF CONSTRAINTS: FLAIR FURNITURE EXAMPLE (10 of 19) Painting Time Constraint and the Feasible Area 2 T + 1 C 100 Any point on line satisfies equation: 2 T + 1 C = 100 (30, 40) yields 100.
GRAPHICAL REPRESENTATION OF CONSTRAINTS: FLAIR FURNITURE EXAMPLE (10 of 19) Painting Time Constraint and the Feasible Area 2 T + 1 C 100 Any point on line satisfies equation: 2 T + 1 C = 100 (30, 40) yields 100.
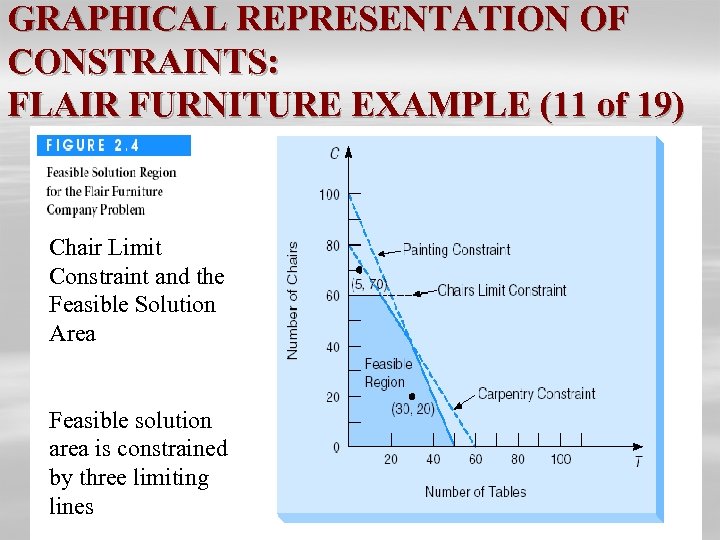 GRAPHICAL REPRESENTATION OF CONSTRAINTS: FLAIR FURNITURE EXAMPLE (11 of 19) Chair Limit Constraint and the Feasible Solution Area Feasible solution area is constrained by three limiting lines
GRAPHICAL REPRESENTATION OF CONSTRAINTS: FLAIR FURNITURE EXAMPLE (11 of 19) Chair Limit Constraint and the Feasible Solution Area Feasible solution area is constrained by three limiting lines
 ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (12 of 19) Ø Let objective function (that is, $7 T + $5 C) guide one towards an optimal point in the feasible region. Ø Plot line representing objective function on graph. Ø One does not know what $7 T + $5 C equals at an optimal solution. Ø Without knowing this value, how does one plot relationship?
ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (12 of 19) Ø Let objective function (that is, $7 T + $5 C) guide one towards an optimal point in the feasible region. Ø Plot line representing objective function on graph. Ø One does not know what $7 T + $5 C equals at an optimal solution. Ø Without knowing this value, how does one plot relationship?
 ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (13 of 19) Ø Write objective function: $7 T + $5 C = Z Ø Select any arbitrary value for Z. Ø For example, one may choose a profit ( Z ) of $210. Ø Z is written as: $7 T + $5 C = $210. Ø To plot this profit line: Set T = 0 and solve objective function for C. Ø Let T = 0, then $7(0) + $5 C = $210, or C = 42. Ø Set C = 0 and solve objective function for T. Ø Let C = 0, then $7 T + $5(0) = $210, or T = 30.
ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (13 of 19) Ø Write objective function: $7 T + $5 C = Z Ø Select any arbitrary value for Z. Ø For example, one may choose a profit ( Z ) of $210. Ø Z is written as: $7 T + $5 C = $210. Ø To plot this profit line: Set T = 0 and solve objective function for C. Ø Let T = 0, then $7(0) + $5 C = $210, or C = 42. Ø Set C = 0 and solve objective function for T. Ø Let C = 0, then $7 T + $5(0) = $210, or T = 30.
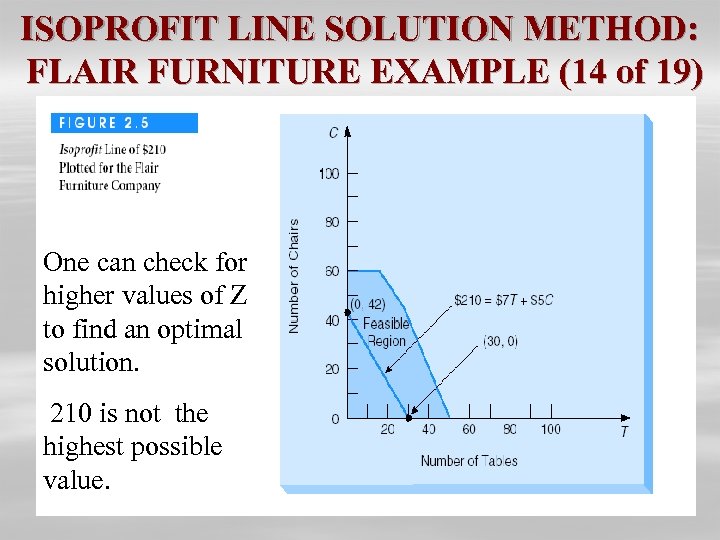 ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (14 of 19) One can check for higher values of Z to find an optimal solution. 210 is not the highest possible value.
ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (14 of 19) One can check for higher values of Z to find an optimal solution. 210 is not the highest possible value.
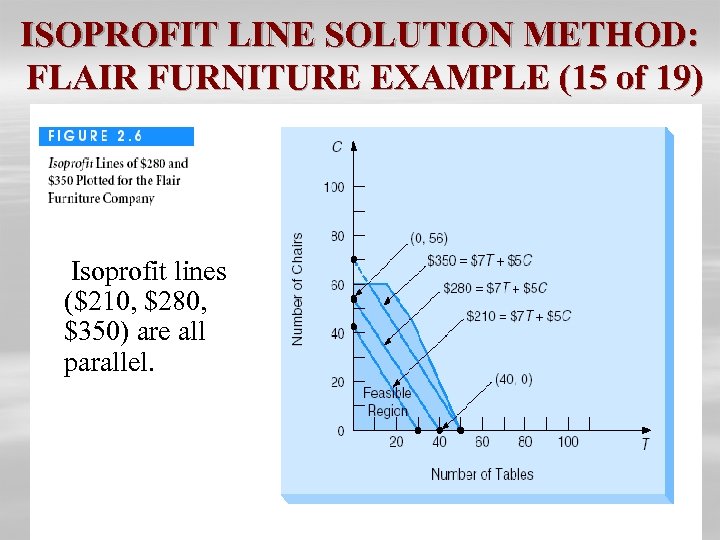 ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (15 of 19) Isoprofit lines ($210, $280, $350) are all parallel.
ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (15 of 19) Isoprofit lines ($210, $280, $350) are all parallel.
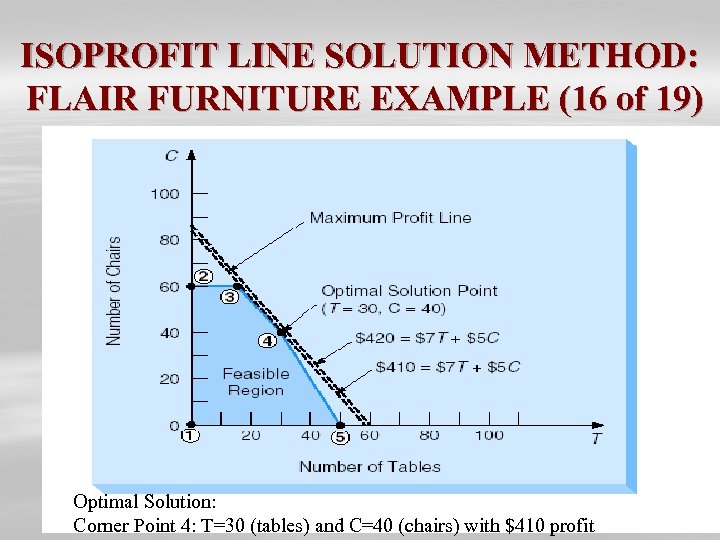 ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (16 of 19) Optimal Solution: Corner Point 4: T=30 (tables) and C=40 (chairs) with $410 profit
ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (16 of 19) Optimal Solution: Corner Point 4: T=30 (tables) and C=40 (chairs) with $410 profit
 ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (17 of 19) Ø Optimal solution occurs at the maximum point in the feasible region. Ø It occurs at the intersection of carpentry and painting constraints: - Carpentry constraint equation: 4 T + 3 C = 240 - Painting constraint equation : 2 T + 1 C = 100 If one solves these two equations with two unknowns for T and C (for Corner Point 4), Optimal Solution is found: T=30 (tables) and C=40 (chairs) with $410 profit.
ISOPROFIT LINE SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (17 of 19) Ø Optimal solution occurs at the maximum point in the feasible region. Ø It occurs at the intersection of carpentry and painting constraints: - Carpentry constraint equation: 4 T + 3 C = 240 - Painting constraint equation : 2 T + 1 C = 100 If one solves these two equations with two unknowns for T and C (for Corner Point 4), Optimal Solution is found: T=30 (tables) and C=40 (chairs) with $410 profit.
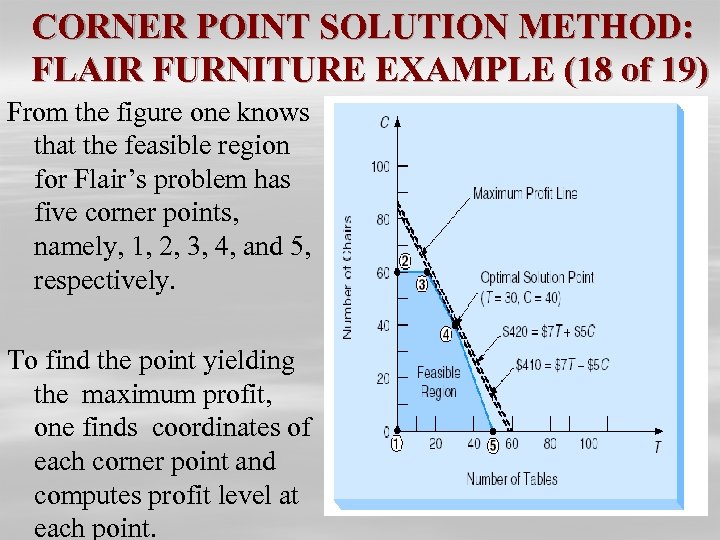 CORNER POINT SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (18 of 19) From the figure one knows that the feasible region for Flair’s problem has five corner points, namely, 1, 2, 3, 4, and 5, respectively. To find the point yielding the maximum profit, one finds coordinates of each corner point and computes profit level at each point.
CORNER POINT SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (18 of 19) From the figure one knows that the feasible region for Flair’s problem has five corner points, namely, 1, 2, 3, 4, and 5, respectively. To find the point yielding the maximum profit, one finds coordinates of each corner point and computes profit level at each point.
 CORNER POINT SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (19 of 19) § Point 1 (T = 0, C = 0) profit = $7(0) + $5(0) = $0 § Point 2 (T = 0, C = 60) profit = $7(0) + $5(60) = $300 § Point 3 (T = 15, C = 60) profit = $7(15) + $5(60) = $405 § Point 4 (T = 30, C = 40) profit = $7(30) + $5(40) = $410 § Point 5 (T = 50, C = 0) profit = $7(50) + $5(0) = $350.
CORNER POINT SOLUTION METHOD: FLAIR FURNITURE EXAMPLE (19 of 19) § Point 1 (T = 0, C = 0) profit = $7(0) + $5(0) = $0 § Point 2 (T = 0, C = 60) profit = $7(0) + $5(60) = $300 § Point 3 (T = 15, C = 60) profit = $7(15) + $5(60) = $405 § Point 4 (T = 30, C = 40) profit = $7(30) + $5(40) = $410 § Point 5 (T = 50, C = 0) profit = $7(50) + $5(0) = $350.
 PROBLEM DEFINITION: THE GALAXY INDUSTRIES EXAMPLE (1 of 9) § Galaxy manufactures two toy models: – Space Ray. – Zapper. § Resources are limited to – 1200 pounds of special plastic. – 40 hours of production time per week.
PROBLEM DEFINITION: THE GALAXY INDUSTRIES EXAMPLE (1 of 9) § Galaxy manufactures two toy models: – Space Ray. – Zapper. § Resources are limited to – 1200 pounds of special plastic. – 40 hours of production time per week.
 PROBLEM DEFINITION: THE GALAXY INDUSTRIES EXAMPLE (2 of 9) Marketing requirement – Total production cannot exceed 800 dozens. – Number of dozens of Space Rays cannot exceed number of dozens of Zappers by more than 450. Technological input – Space Rays requires 2 pounds of plastic and 3 minutes of labor per dozen. – Zappers requires 1 pound of plastic and 4 minutes of labor per dozen.
PROBLEM DEFINITION: THE GALAXY INDUSTRIES EXAMPLE (2 of 9) Marketing requirement – Total production cannot exceed 800 dozens. – Number of dozens of Space Rays cannot exceed number of dozens of Zappers by more than 450. Technological input – Space Rays requires 2 pounds of plastic and 3 minutes of labor per dozen. – Zappers requires 1 pound of plastic and 4 minutes of labor per dozen.
 PROBLEM DEFINITION: THE GALAXY INDUSTRIES EXAMPLE (3 of 9) Current production plan calls for: – Producing as much as possible of the more profitable product, Space Ray ($8 profit per dozen). – Use resources left over to produce Zappers ($5 profit per dozen). The current production plan consists of: Space Rays = 550 dozens Zapper = 100 dozens Profit = 4900 dollars per week
PROBLEM DEFINITION: THE GALAXY INDUSTRIES EXAMPLE (3 of 9) Current production plan calls for: – Producing as much as possible of the more profitable product, Space Ray ($8 profit per dozen). – Use resources left over to produce Zappers ($5 profit per dozen). The current production plan consists of: Space Rays = 550 dozens Zapper = 100 dozens Profit = 4900 dollars per week
 Management is seeking a production schedule that will increase the company’s profit.
Management is seeking a production schedule that will increase the company’s profit.
 DECISION VARIABLES: GALAXY INDUSTRIES EXAMPLE (4 of 9) § Decision variables: – X 1 = Production level of Space Rays (in dozens per week). – X 2 = Production level of Zappers (in dozens per week). § Objective Function: - Weekly profit, to be maximized
DECISION VARIABLES: GALAXY INDUSTRIES EXAMPLE (4 of 9) § Decision variables: – X 1 = Production level of Space Rays (in dozens per week). – X 2 = Production level of Zappers (in dozens per week). § Objective Function: - Weekly profit, to be maximized
 BUILDING THE COMPLETE MATHEMATICAL MODEL: GALAXY INDUSTRIES EXAMPLE (5 of 9) Max. 8 X 1 + 5 X 2 (Weekly profit) subject to 2 X 1 + 1 X 2 < = 1200 (Plastic) 3 X 1 + 4 X 2 < = 2400 (Production Time) X 1 + X 2 < = 800 (Total production) X 1 - X 2 < = 450 (Mix) Xj> = 0, j = 1, 2 (Nonnegativity)
BUILDING THE COMPLETE MATHEMATICAL MODEL: GALAXY INDUSTRIES EXAMPLE (5 of 9) Max. 8 X 1 + 5 X 2 (Weekly profit) subject to 2 X 1 + 1 X 2 < = 1200 (Plastic) 3 X 1 + 4 X 2 < = 2400 (Production Time) X 1 + X 2 < = 800 (Total production) X 1 - X 2 < = 450 (Mix) Xj> = 0, j = 1, 2 (Nonnegativity)
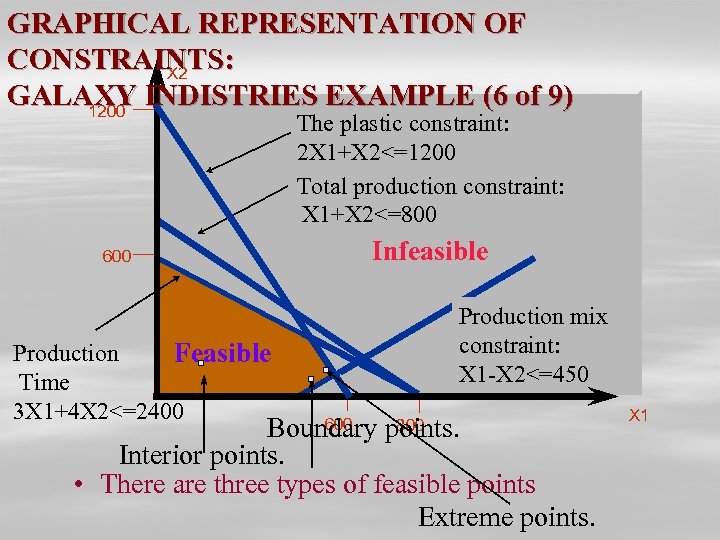 GRAPHICAL REPRESENTATION OF CONSTRAINTS: X 2 GALAXY INDISTRIES EXAMPLE (6 of 9) 1200 The plastic constraint: The Plastic constraint 2 X 1+X 2<=1200 Total production constraint: X 1+X 2<=800 Infeasible 600 Production Feasible Time 3 X 1+4 X 2<=2400 Production mix constraint: X 1 -X 2<=450 Boundary points. Interior points. • There are three types of feasible points Extreme points. 600 800 X 1
GRAPHICAL REPRESENTATION OF CONSTRAINTS: X 2 GALAXY INDISTRIES EXAMPLE (6 of 9) 1200 The plastic constraint: The Plastic constraint 2 X 1+X 2<=1200 Total production constraint: X 1+X 2<=800 Infeasible 600 Production Feasible Time 3 X 1+4 X 2<=2400 Production mix constraint: X 1 -X 2<=450 Boundary points. Interior points. • There are three types of feasible points Extreme points. 600 800 X 1
 SOLVING GRAPHICALLY FOR AN OPTIMAL SOLUTION
SOLVING GRAPHICALLY FOR AN OPTIMAL SOLUTION
 ISOPROFIT LINE SOLUTION METHOD: GALAXY INDUSTRIES EXAMPLE (7 of 9) We now demonstrate the search for an optimal solution X 2 Start at some arbitrary profit, say profit = $2, 000. . . 1200 Then increase the profit, if possible. . . ion. . . and continue until it becomes infeasible eg 800 Profit 3, =$5040 4, Profit = $ 2, 000 the ll asi fe e. R bl eca R 600 X 1 400 600 800
ISOPROFIT LINE SOLUTION METHOD: GALAXY INDUSTRIES EXAMPLE (7 of 9) We now demonstrate the search for an optimal solution X 2 Start at some arbitrary profit, say profit = $2, 000. . . 1200 Then increase the profit, if possible. . . ion. . . and continue until it becomes infeasible eg 800 Profit 3, =$5040 4, Profit = $ 2, 000 the ll asi fe e. R bl eca R 600 X 1 400 600 800
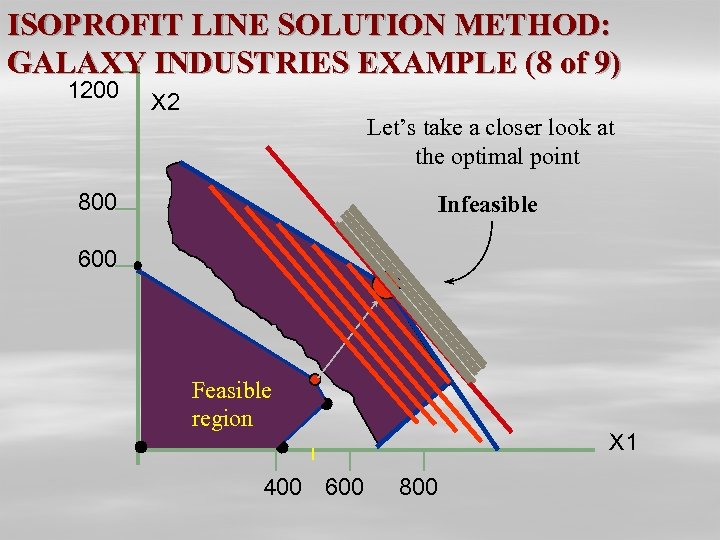 ISOPROFIT LINE SOLUTION METHOD: GALAXY INDUSTRIES EXAMPLE (8 of 9) 1200 X 2 Let’s take a closer look at the optimal point 800 Infeasible 600 Feasible region 400 X 1 600 800
ISOPROFIT LINE SOLUTION METHOD: GALAXY INDUSTRIES EXAMPLE (8 of 9) 1200 X 2 Let’s take a closer look at the optimal point 800 Infeasible 600 Feasible region 400 X 1 600 800
 OPTIMAL SOLUTION: GALAXY INDUSTRIES EXAMPLE (9 of 9) Space Rays = 480 dozens Zappers = 240 dozens Profit = $5040 – This solution utilizes all the plastic and all the production hours. – Total production is only 720 (not 800). – Space Rays production exceeds Zapper by only 240 dozens (not 450).
OPTIMAL SOLUTION: GALAXY INDUSTRIES EXAMPLE (9 of 9) Space Rays = 480 dozens Zappers = 240 dozens Profit = $5040 – This solution utilizes all the plastic and all the production hours. – Total production is only 720 (not 800). – Space Rays production exceeds Zapper by only 240 dozens (not 450).
 § § § MINIMIZATION MODEL EXAMPLES: FERTILIZER MIX PROBLEM HOLIDAY MEAL CHICKEN RANCH EXAMPLE NAVY SEA RATIONS EXAMPLE
§ § § MINIMIZATION MODEL EXAMPLES: FERTILIZER MIX PROBLEM HOLIDAY MEAL CHICKEN RANCH EXAMPLE NAVY SEA RATIONS EXAMPLE
 A MINIMIZATION LP PROBLEM Many LP problems involve minimizing objective such as cost instead of maximizing profit function. Examples: – Restaurant may wish to develop work schedule to meet staffing needs while minimizing total number of employees. – Manufacturer may seek to distribute its products from several factories to its many regional warehouses in such a way as to minimize total shipping costs. – Hospital may want to provide its patients with a daily meal plan that meets certain nutritional standards while minimizing food purchase costs.
A MINIMIZATION LP PROBLEM Many LP problems involve minimizing objective such as cost instead of maximizing profit function. Examples: – Restaurant may wish to develop work schedule to meet staffing needs while minimizing total number of employees. – Manufacturer may seek to distribute its products from several factories to its many regional warehouses in such a way as to minimize total shipping costs. – Hospital may want to provide its patients with a daily meal plan that meets certain nutritional standards while minimizing food purchase costs.
 PROBLEM DEFINITION: FERTILIZER MIX EXAMPLE (1 of 7) Ø Two brands of fertilizer available - Super-Gro, Crop-Quick. Ø Field requires at least 16 pounds of nitrogen and 24 pounds of phosphate. Ø Super-Gro costs $6 per bag, Crop-Quick $3 per bag. Ø Problem: How much of each brand to purchase to minimize total cost of fertilizer given the following data ?
PROBLEM DEFINITION: FERTILIZER MIX EXAMPLE (1 of 7) Ø Two brands of fertilizer available - Super-Gro, Crop-Quick. Ø Field requires at least 16 pounds of nitrogen and 24 pounds of phosphate. Ø Super-Gro costs $6 per bag, Crop-Quick $3 per bag. Ø Problem: How much of each brand to purchase to minimize total cost of fertilizer given the following data ?
 PROBLEM DEFINITION: FERTILIZER MIX EXAMPLE (2 of 7) Decision Variables: x 1 = bags of Super-Gro x 2 = bags of Crop-Quick The Objective Function: Minimize Z = $6 x 1 + 3 x 2 Model Constraints: 2 x 1 + 4 x 2 16 lb (nitrogen constraint) 4 x 1 + 3 x 2 24 lb (phosphate constraint) x 1, x 2 0 (non-negativity constraint)
PROBLEM DEFINITION: FERTILIZER MIX EXAMPLE (2 of 7) Decision Variables: x 1 = bags of Super-Gro x 2 = bags of Crop-Quick The Objective Function: Minimize Z = $6 x 1 + 3 x 2 Model Constraints: 2 x 1 + 4 x 2 16 lb (nitrogen constraint) 4 x 1 + 3 x 2 24 lb (phosphate constraint) x 1, x 2 0 (non-negativity constraint)
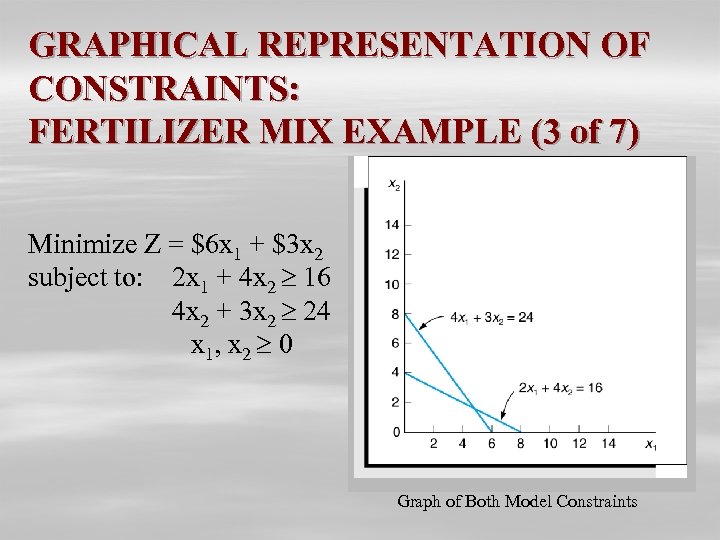 GRAPHICAL REPRESENTATION OF CONSTRAINTS: FERTILIZER MIX EXAMPLE (3 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 2 + 3 x 2 24 x 1, x 2 0 Graph of Both Model Constraints
GRAPHICAL REPRESENTATION OF CONSTRAINTS: FERTILIZER MIX EXAMPLE (3 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 2 + 3 x 2 24 x 1, x 2 0 Graph of Both Model Constraints
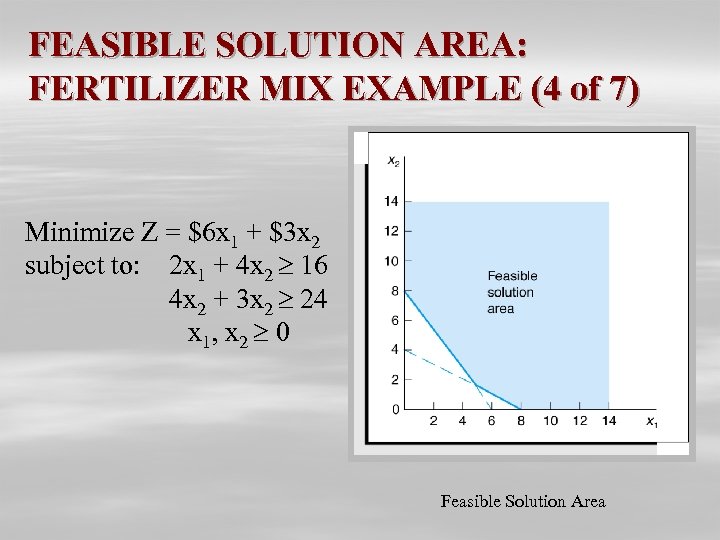 FEASIBLE SOLUTION AREA: FERTILIZER MIX EXAMPLE (4 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 2 + 3 x 2 24 x 1, x 2 0 Feasible Solution Area
FEASIBLE SOLUTION AREA: FERTILIZER MIX EXAMPLE (4 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 2 + 3 x 2 24 x 1, x 2 0 Feasible Solution Area
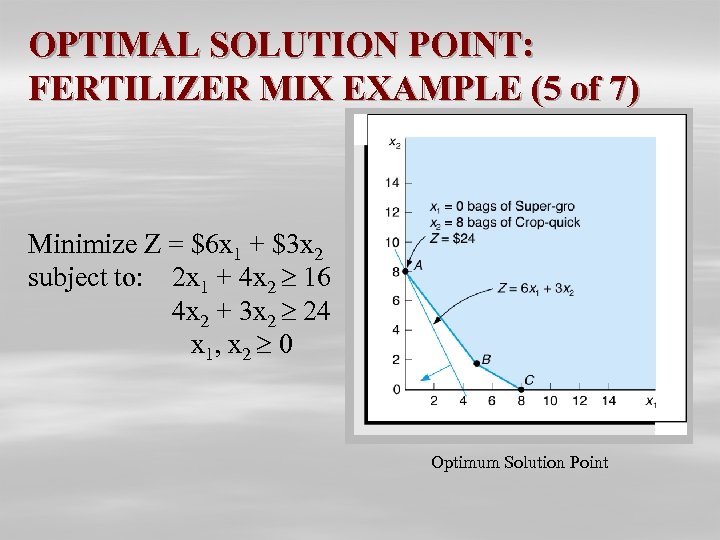 OPTIMAL SOLUTION POINT: FERTILIZER MIX EXAMPLE (5 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 2 + 3 x 2 24 x 1, x 2 0 Optimum Solution Point
OPTIMAL SOLUTION POINT: FERTILIZER MIX EXAMPLE (5 of 7) Minimize Z = $6 x 1 + $3 x 2 subject to: 2 x 1 + 4 x 2 16 4 x 2 + 3 x 2 24 x 1, x 2 0 Optimum Solution Point
 SURPLUS VARIABLES: FERTILIZER MIX EXAMPLE (6 of 7) § A surplus variable is subtracted from a constraint to convert it to an equation (=). § A surplus variable represents an excess above a constraint requirement level. § Surplus variables contribute nothing to the calculated value of the objective function. § Subtracting surplus variables in the farmer problem constraints: 2 x 1 + 4 x 2 - s 1 = 16 (nitrogen) 4 x 1 + 3 x 2 - s 2 = 24 (phosphate)
SURPLUS VARIABLES: FERTILIZER MIX EXAMPLE (6 of 7) § A surplus variable is subtracted from a constraint to convert it to an equation (=). § A surplus variable represents an excess above a constraint requirement level. § Surplus variables contribute nothing to the calculated value of the objective function. § Subtracting surplus variables in the farmer problem constraints: 2 x 1 + 4 x 2 - s 1 = 16 (nitrogen) 4 x 1 + 3 x 2 - s 2 = 24 (phosphate)
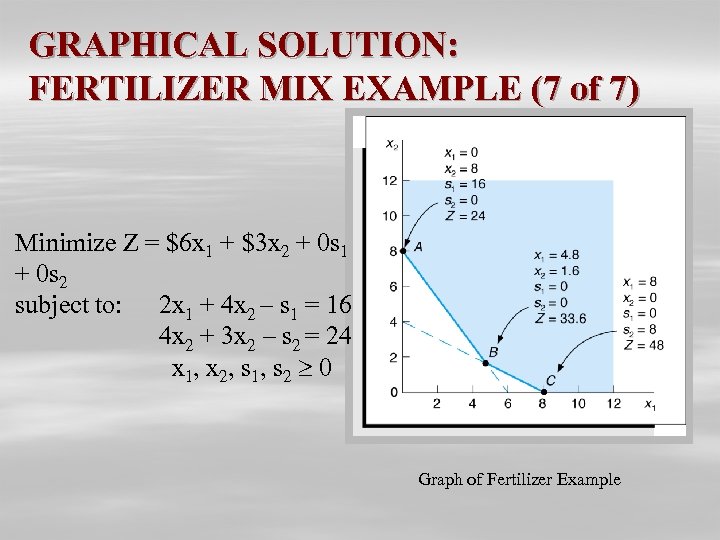 GRAPHICAL SOLUTION: FERTILIZER MIX EXAMPLE (7 of 7) Minimize Z = $6 x 1 + $3 x 2 + 0 s 1 + 0 s 2 subject to: 2 x 1 + 4 x 2 – s 1 = 16 4 x 2 + 3 x 2 – s 2 = 24 x 1, x 2, s 1, s 2 0 Graph of Fertilizer Example
GRAPHICAL SOLUTION: FERTILIZER MIX EXAMPLE (7 of 7) Minimize Z = $6 x 1 + $3 x 2 + 0 s 1 + 0 s 2 subject to: 2 x 1 + 4 x 2 – s 1 = 16 4 x 2 + 3 x 2 – s 2 = 24 x 1, x 2, s 1, s 2 0 Graph of Fertilizer Example
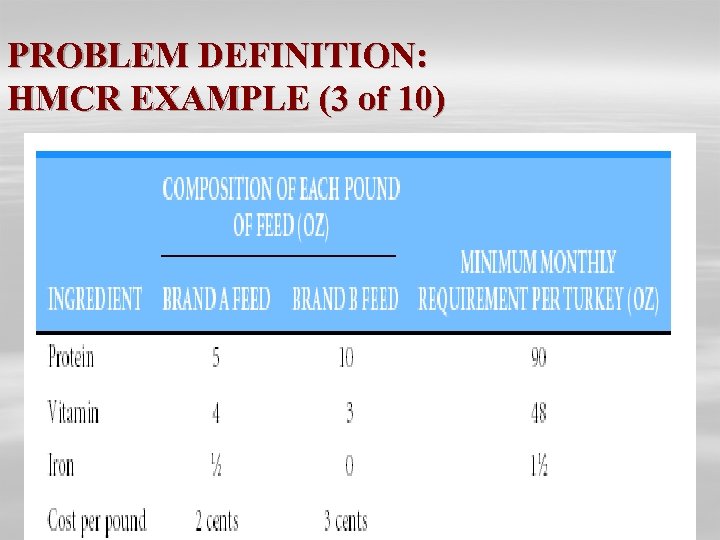
 PROBLEM DEFINITION: HOLIDAY MEAL CHICKEN RANCH (HMCR) EXAMPLE (1 of 10) Ø Buy two brands of feed for good, low-cost diet for chickens. Ø Each feed may contain three nutritional ingredients (protein, vitamin, and iron). Ø One pound of Brand A contains: Ø 5 units of protein, Ø 4 units of vitamin, and Ø 0. 5 units of iron. Ø One pound of Brand B contains: Ø 10 units of protein, Ø 3 units of vitamin, and Ø 0 units of iron.
PROBLEM DEFINITION: HOLIDAY MEAL CHICKEN RANCH (HMCR) EXAMPLE (1 of 10) Ø Buy two brands of feed for good, low-cost diet for chickens. Ø Each feed may contain three nutritional ingredients (protein, vitamin, and iron). Ø One pound of Brand A contains: Ø 5 units of protein, Ø 4 units of vitamin, and Ø 0. 5 units of iron. Ø One pound of Brand B contains: Ø 10 units of protein, Ø 3 units of vitamin, and Ø 0 units of iron.
 PROBLEM DEFINITION: HMCR EXAMPLE (2 of 10) Brand A feed costs ranch $0. 02 per pound, while Brand B feed costs $0. 03 per pound. Ranch owner would like lowest-cost diet that meets minimum monthly intake requirements for each nutritional ingredient.
PROBLEM DEFINITION: HMCR EXAMPLE (2 of 10) Brand A feed costs ranch $0. 02 per pound, while Brand B feed costs $0. 03 per pound. Ranch owner would like lowest-cost diet that meets minimum monthly intake requirements for each nutritional ingredient.
 PROBLEM DEFINITION: HMCR EXAMPLE (3 of 10)
PROBLEM DEFINITION: HMCR EXAMPLE (3 of 10)
 BUILDING THE COMPLETE MATHEMATICAL MODEL: HMCR EXAMPLE (4 of 10) Minimize cost (in cents) = 2 A + 3 B Subject to: 5 A + 10 B 90 (protein constraint) 4 A + 3 B 48 (vitamin constraint) ½A 1½ (iron constraint) A 0, B 0 (nonnegativity constraint) Where: A denotes number of pounds of Brand A feed, and B denote number of pounds of Brand B feed.
BUILDING THE COMPLETE MATHEMATICAL MODEL: HMCR EXAMPLE (4 of 10) Minimize cost (in cents) = 2 A + 3 B Subject to: 5 A + 10 B 90 (protein constraint) 4 A + 3 B 48 (vitamin constraint) ½A 1½ (iron constraint) A 0, B 0 (nonnegativity constraint) Where: A denotes number of pounds of Brand A feed, and B denote number of pounds of Brand B feed.
 BUILDING THE STANDARD LP MODEL: HMCR EXAMPLE (5 of 10) Minimize cost (in cents)=2 A+3 B+0 s 1+0 s 2+0 s 3 subject to constraints: 5 A + 10 B - s 1 = 90 (protein constraint) 4 A + 3 B - s 2 = 48 (vitamin constraint) ½A - s 3 = 1½ (iron constraint) A, B, s 1, s 2 s 3 0 (nonnegativity)
BUILDING THE STANDARD LP MODEL: HMCR EXAMPLE (5 of 10) Minimize cost (in cents)=2 A+3 B+0 s 1+0 s 2+0 s 3 subject to constraints: 5 A + 10 B - s 1 = 90 (protein constraint) 4 A + 3 B - s 2 = 48 (vitamin constraint) ½A - s 3 = 1½ (iron constraint) A, B, s 1, s 2 s 3 0 (nonnegativity)
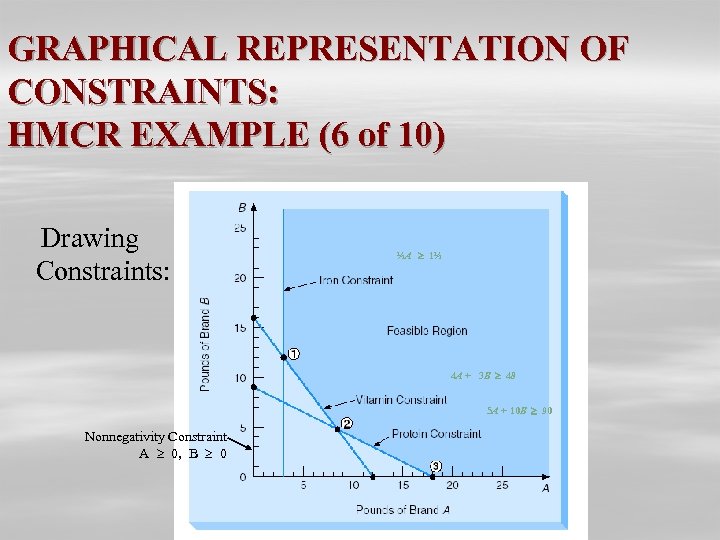 GRAPHICAL REPRESENTATION OF CONSTRAINTS: HMCR EXAMPLE (6 of 10) Drawing Constraints: ½A 1½ 4 A + 3 B 48 5 A + 10 B 90 Nonnegativity Constraint A 0, B 0
GRAPHICAL REPRESENTATION OF CONSTRAINTS: HMCR EXAMPLE (6 of 10) Drawing Constraints: ½A 1½ 4 A + 3 B 48 5 A + 10 B 90 Nonnegativity Constraint A 0, B 0
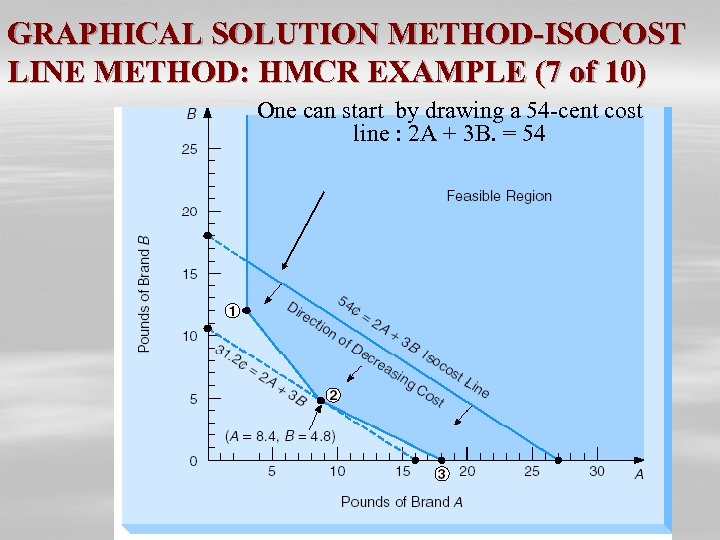 GRAPHICAL SOLUTION METHOD-ISOCOST LINE METHOD: HMCR EXAMPLE (7 of 10) One can start by drawing a 54 -cent cost line : 2 A + 3 B. = 54
GRAPHICAL SOLUTION METHOD-ISOCOST LINE METHOD: HMCR EXAMPLE (7 of 10) One can start by drawing a 54 -cent cost line : 2 A + 3 B. = 54
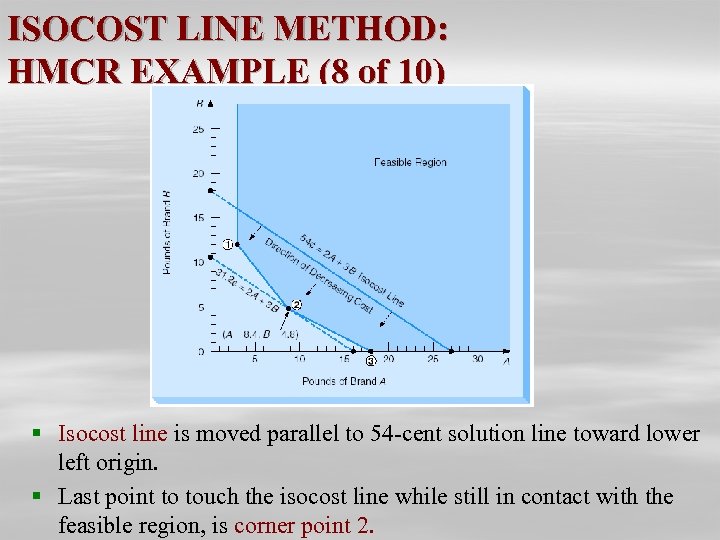 ISOCOST LINE METHOD: HMCR EXAMPLE (8 of 10) § Isocost line is moved parallel to 54 -cent solution line toward lower left origin. § Last point to touch the isocost line while still in contact with the feasible region, is corner point 2.
ISOCOST LINE METHOD: HMCR EXAMPLE (8 of 10) § Isocost line is moved parallel to 54 -cent solution line toward lower left origin. § Last point to touch the isocost line while still in contact with the feasible region, is corner point 2.
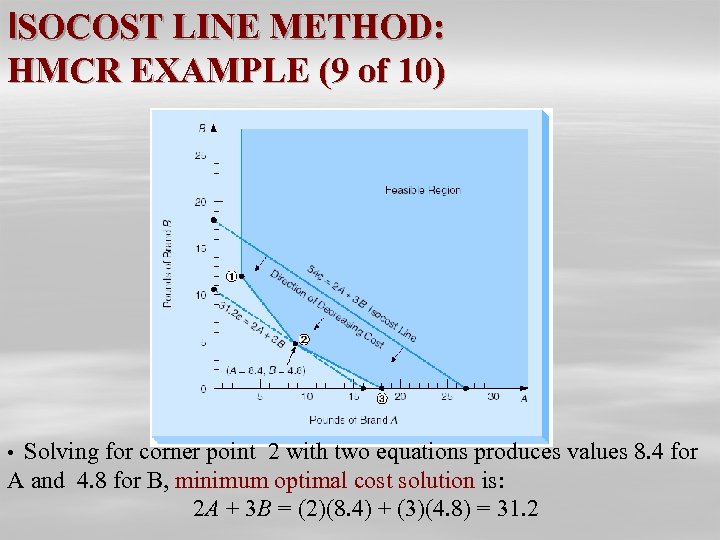 ISOCOST LINE METHOD: HMCR EXAMPLE (9 of 10) • Solving for corner point 2 with two equations produces values 8. 4 for A and 4. 8 for B, minimum optimal cost solution is: 2 A + 3 B = (2)(8. 4) + (3)(4. 8) = 31. 2
ISOCOST LINE METHOD: HMCR EXAMPLE (9 of 10) • Solving for corner point 2 with two equations produces values 8. 4 for A and 4. 8 for B, minimum optimal cost solution is: 2 A + 3 B = (2)(8. 4) + (3)(4. 8) = 31. 2
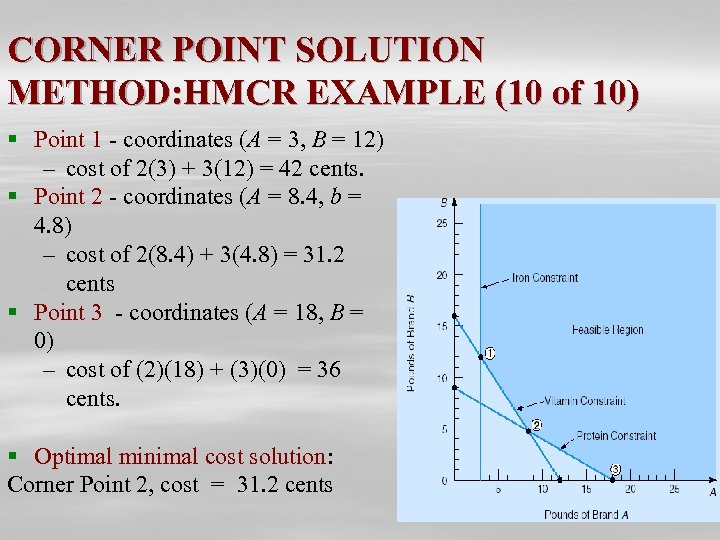 CORNER POINT SOLUTION METHOD: HMCR EXAMPLE (10 of 10) § Point 1 - coordinates (A = 3, B = 12) – cost of 2(3) + 3(12) = 42 cents. § Point 2 - coordinates (A = 8. 4, b = 4. 8) – cost of 2(8. 4) + 3(4. 8) = 31. 2 cents § Point 3 - coordinates (A = 18, B = 0) – cost of (2)(18) + (3)(0) = 36 cents. § Optimal minimal cost solution: Corner Point 2, cost = 31. 2 cents
CORNER POINT SOLUTION METHOD: HMCR EXAMPLE (10 of 10) § Point 1 - coordinates (A = 3, B = 12) – cost of 2(3) + 3(12) = 42 cents. § Point 2 - coordinates (A = 8. 4, b = 4. 8) – cost of 2(8. 4) + 3(4. 8) = 31. 2 cents § Point 3 - coordinates (A = 18, B = 0) – cost of (2)(18) + (3)(0) = 36 cents. § Optimal minimal cost solution: Corner Point 2, cost = 31. 2 cents
 PROBLEM DEFINITION: NAVY SEA RATIONS EXAMPLE (1 of 4) • A cost minimization diet problem – Mix two sea ration products: Texfoods, Calration. – Minimize the total cost of the mix. – Meet the minimum requirements of Vitamin A, Vitamin D, and Iron.
PROBLEM DEFINITION: NAVY SEA RATIONS EXAMPLE (1 of 4) • A cost minimization diet problem – Mix two sea ration products: Texfoods, Calration. – Minimize the total cost of the mix. – Meet the minimum requirements of Vitamin A, Vitamin D, and Iron.
 COMPLETE MODEL: NAVY SEA RATIONS EXAMPLE (2 of 4) § Decision variables: – X 1 (X 2) -- The number of portions of Texfoods (Calration) product used in a serving. § The Model: Minimize 0. 60 X 1 + 0. 50 X 2 Subject to 20 X 1 + 50 X 2 ≥ 100 Vitamin A 25 X 1 + 25 X 2 ≥ 100 Vitamin D 50 X 1 + 10 X 2 ≥ 100 Iron X 1, X 2 ≥ 0
COMPLETE MODEL: NAVY SEA RATIONS EXAMPLE (2 of 4) § Decision variables: – X 1 (X 2) -- The number of portions of Texfoods (Calration) product used in a serving. § The Model: Minimize 0. 60 X 1 + 0. 50 X 2 Subject to 20 X 1 + 50 X 2 ≥ 100 Vitamin A 25 X 1 + 25 X 2 ≥ 100 Vitamin D 50 X 1 + 10 X 2 ≥ 100 Iron X 1, X 2 ≥ 0
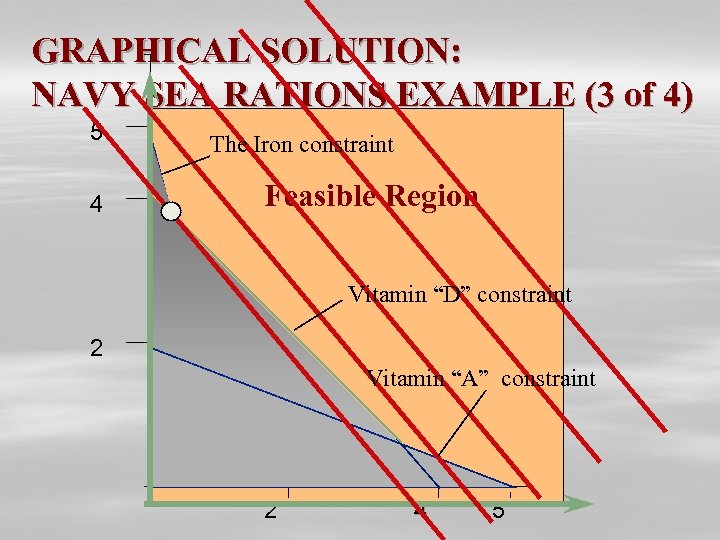 GRAPHICAL SOLUTION: NAVY SEA RATIONS EXAMPLE (3 of 4) 5 4 The Iron constraint Feasible Region Vitamin “D” constraint 2 Vitamin “A” constraint 2 4 5
GRAPHICAL SOLUTION: NAVY SEA RATIONS EXAMPLE (3 of 4) 5 4 The Iron constraint Feasible Region Vitamin “D” constraint 2 Vitamin “A” constraint 2 4 5
 SUMMARY OF THE OPTIMAL SOLUTION: NAVY SEA RATIONS EXAMPLE (4 of 4) – Texfood product = 1. 5 portions – Calration product = 2. 5 portions – Cost =$ 2. 15 per serving. – The minimum requirement for Vitamin D and iron are met with no surplus. – The mixture provides 155% of the requirement for Vitamine A.
SUMMARY OF THE OPTIMAL SOLUTION: NAVY SEA RATIONS EXAMPLE (4 of 4) – Texfood product = 1. 5 portions – Calration product = 2. 5 portions – Cost =$ 2. 15 per serving. – The minimum requirement for Vitamin D and iron are met with no surplus. – The mixture provides 155% of the requirement for Vitamine A.
 SUMMARY OF THE GRAPHICAL SOLUTION METHODS (1 of 3) 1. Plot the model constraints accepting them as equalities, 2. Considering the inequalities of the constraints identify the feasible solution region, that is, the area that satisfies all constraints simultaneously. 3. Select one of two following graphical solution techniques and proceed to solve problem. - Isoprofit or Isocost Method. - Corner Point Method
SUMMARY OF THE GRAPHICAL SOLUTION METHODS (1 of 3) 1. Plot the model constraints accepting them as equalities, 2. Considering the inequalities of the constraints identify the feasible solution region, that is, the area that satisfies all constraints simultaneously. 3. Select one of two following graphical solution techniques and proceed to solve problem. - Isoprofit or Isocost Method. - Corner Point Method
 SUMMARY OF THE GRAPHICAL SOLUTION METHODS (2 of 3) Corner Point Method Ø Determine the coordinates of each of the corner points of the feasible region by solving simultaneous equations at each point. Ø Compute the profit or cost at each point by substituting the values of coordinates into the objective function and solving for results. Ø Identify the optimal solution as a corner point with highest profit (maximization), or lowest cost (minimization).
SUMMARY OF THE GRAPHICAL SOLUTION METHODS (2 of 3) Corner Point Method Ø Determine the coordinates of each of the corner points of the feasible region by solving simultaneous equations at each point. Ø Compute the profit or cost at each point by substituting the values of coordinates into the objective function and solving for results. Ø Identify the optimal solution as a corner point with highest profit (maximization), or lowest cost (minimization).
 SUMMARY OF THE GRAPHICAL SOLUTION METHODS (3 of 3) Isoprofit or Isocost Method Ø Select an arbitrary value for profit or cost, and plot an isoprofit / isocost line to reveal its slope. Ø Maintain the same slope and move the line up or down until it touches the feasible region at one point. While moving the line up or down consider whether the problem is a maximization or a minimization problem Ø Identify the optimal solution as coordinates of the point that is touched by the highest possible isoprofit line or lowest possible isocost line (by solving the simultaneous equations) Ø Read optimal coordinates and compute the optimal profit
SUMMARY OF THE GRAPHICAL SOLUTION METHODS (3 of 3) Isoprofit or Isocost Method Ø Select an arbitrary value for profit or cost, and plot an isoprofit / isocost line to reveal its slope. Ø Maintain the same slope and move the line up or down until it touches the feasible region at one point. While moving the line up or down consider whether the problem is a maximization or a minimization problem Ø Identify the optimal solution as coordinates of the point that is touched by the highest possible isoprofit line or lowest possible isocost line (by solving the simultaneous equations) Ø Read optimal coordinates and compute the optimal profit
 SPECIAL SITUATIONS IN SOLVING LP PROBLEMS (IRREGULAR TYPES OF LP PROBLEMS)
SPECIAL SITUATIONS IN SOLVING LP PROBLEMS (IRREGULAR TYPES OF LP PROBLEMS)
 IRREGULAR TYPES OF LINEAR PROGRAMMING PROBLEMS Ø For some linear programming models, the general rules do not apply. Ø Special types of problems include those with: ØRedundancy ØInfeasible solutions ØUnbounded solutions ØMultiple optimal solutions
IRREGULAR TYPES OF LINEAR PROGRAMMING PROBLEMS Ø For some linear programming models, the general rules do not apply. Ø Special types of problems include those with: ØRedundancy ØInfeasible solutions ØUnbounded solutions ØMultiple optimal solutions
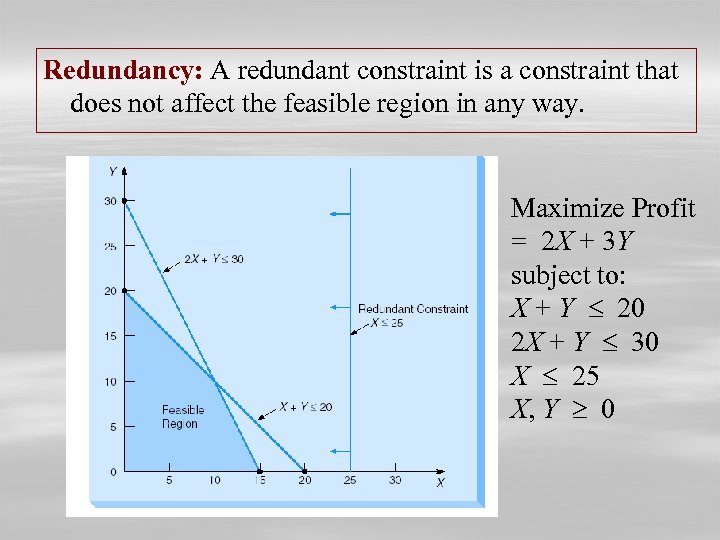 Redundancy: A redundant constraint is a constraint that does not affect the feasible region in any way. Maximize Profit = 2 X + 3 Y subject to: X + Y 20 2 X + Y 30 X 25 X, Y 0
Redundancy: A redundant constraint is a constraint that does not affect the feasible region in any way. Maximize Profit = 2 X + 3 Y subject to: X + Y 20 2 X + Y 30 X 25 X, Y 0
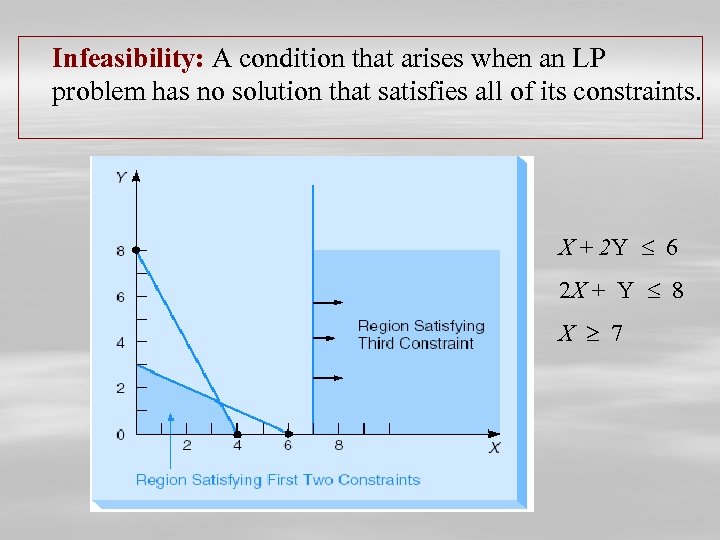 Infeasibility: A condition that arises when an LP problem has no solution that satisfies all of its constraints. X + 2 Y 6 2 X + Y 8 X 7
Infeasibility: A condition that arises when an LP problem has no solution that satisfies all of its constraints. X + 2 Y 6 2 X + Y 8 X 7
 Unboundedness: Sometimes an LP model will not have a finite solution Maximize profit = $3 X + $5 Y subject to: X 5 Y 10 X + 2 Y 10 X, Y 0
Unboundedness: Sometimes an LP model will not have a finite solution Maximize profit = $3 X + $5 Y subject to: X 5 Y 10 X + 2 Y 10 X, Y 0
 MULTIPLE OPTIMAL SOLUTIONS § An LP problem may have more than one optimal solution. – Graphically, when the isoprofit (or isocost) line runs parallel to a constraint in the problem which lies in the direction in which isoprofit (or isocost) line is located. – In other words, when they have the same slope.
MULTIPLE OPTIMAL SOLUTIONS § An LP problem may have more than one optimal solution. – Graphically, when the isoprofit (or isocost) line runs parallel to a constraint in the problem which lies in the direction in which isoprofit (or isocost) line is located. – In other words, when they have the same slope.
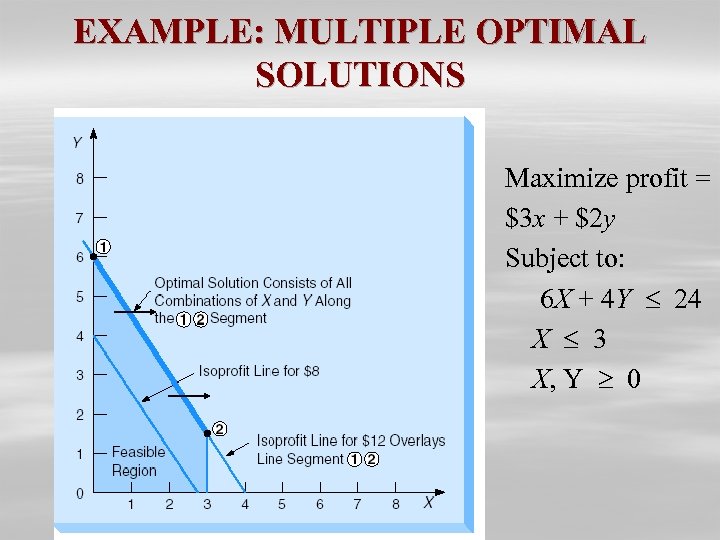 EXAMPLE: MULTIPLE OPTIMAL SOLUTIONS Maximize profit = $3 x + $2 y Subject to: 6 X + 4 Y 24 X 3 X, Y 0
EXAMPLE: MULTIPLE OPTIMAL SOLUTIONS Maximize profit = $3 x + $2 y Subject to: 6 X + 4 Y 24 X 3 X, Y 0
 EXAMPLE: MULTIPLE OPTIMAL SOLUTIONS Ø At profit level of $12, isoprofit line will rest directly on top of first constraint line. Ø This means that any point along the line between corner points 1 and 2 provides an optimal X and Y combination.
EXAMPLE: MULTIPLE OPTIMAL SOLUTIONS Ø At profit level of $12, isoprofit line will rest directly on top of first constraint line. Ø This means that any point along the line between corner points 1 and 2 provides an optimal X and Y combination.
 SETTING UP AND SOLVING LP PROBLEMS USING EXCEL’S SOLVER Using solver to solve Flair Furniture problem: Recall decision variables T ( Tables ) and C ( Chairs ) in Flair Furniture problem: Maximize profit = $7 T + $5 C Subject to constraints 4 T + 3 C 240 (carpentry constraint) 2 T + 1 C 100 (painting constraint) C 60 (chairs limit constraint) T, C 0 (non-negativity)
SETTING UP AND SOLVING LP PROBLEMS USING EXCEL’S SOLVER Using solver to solve Flair Furniture problem: Recall decision variables T ( Tables ) and C ( Chairs ) in Flair Furniture problem: Maximize profit = $7 T + $5 C Subject to constraints 4 T + 3 C 240 (carpentry constraint) 2 T + 1 C 100 (painting constraint) C 60 (chairs limit constraint) T, C 0 (non-negativity)
 SOLVER SPREADSHEET SETUP
SOLVER SPREADSHEET SETUP
 LP EXCEL AND SOLVER PARTS Changing cells § Solver refers to decision variables as changing cells. § In Flair Furniture example, there are two decision variables cells B 5 and C 5 to represent number of tables to make (T) and number of chairs to make (C), respectively.
LP EXCEL AND SOLVER PARTS Changing cells § Solver refers to decision variables as changing cells. § In Flair Furniture example, there are two decision variables cells B 5 and C 5 to represent number of tables to make (T) and number of chairs to make (C), respectively.
 LP EXCEL AND SOLVER PARTS Changing Cells § In each of excel layouts, for clarity, changing cells (decision variables) have been shaded yellow. Changing Cells ( B 5 and C 5 )
LP EXCEL AND SOLVER PARTS Changing Cells § In each of excel layouts, for clarity, changing cells (decision variables) have been shaded yellow. Changing Cells ( B 5 and C 5 )
 LP EXCEL AND SOLVER PARTS Target Cell Objective function, referred to as target cell by solver, = SUMPRODUCT(B 6: C 6, $B$5: $C$5) This is equivalent to =B 6*B 5+C 6*C 5 Target Cell
LP EXCEL AND SOLVER PARTS Target Cell Objective function, referred to as target cell by solver, = SUMPRODUCT(B 6: C 6, $B$5: $C$5) This is equivalent to =B 6*B 5+C 6*C 5 Target Cell
 LP EXCEL AND SOLVER PARTS Constraints Each constraint has three parts - (1) A left hand side (LHS) part consisting of every term to the left of the equality or inequality sign. (2) A right hand side (RHS) part consisting of all terms to the right of the equality or inequality sign. (3) An equality or inequality sign.
LP EXCEL AND SOLVER PARTS Constraints Each constraint has three parts - (1) A left hand side (LHS) part consisting of every term to the left of the equality or inequality sign. (2) A right hand side (RHS) part consisting of all terms to the right of the equality or inequality sign. (3) An equality or inequality sign.
 LP EXCEL AND SOLVER PARTS Constraints Each constraint has three parts 1. A left hand side (LHS) part. 2. A right hand side (RHS) part. 3. Equality or inequality sign. 1 3 2
LP EXCEL AND SOLVER PARTS Constraints Each constraint has three parts 1. A left hand side (LHS) part. 2. A right hand side (RHS) part. 3. Equality or inequality sign. 1 3 2
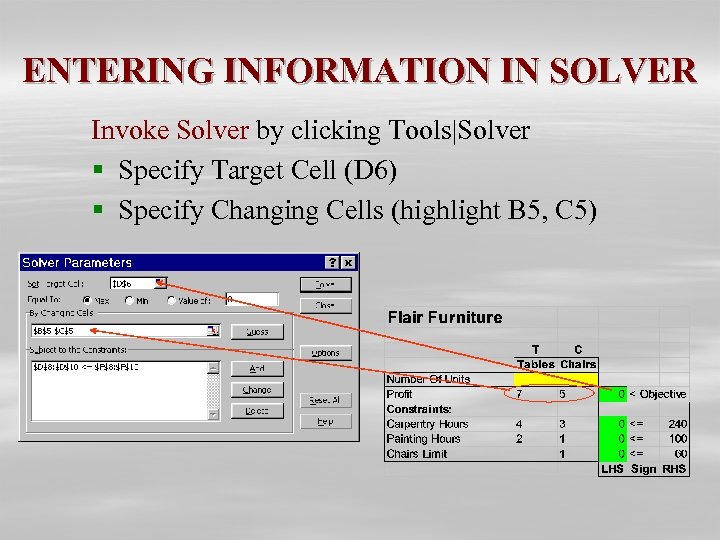 ENTERING INFORMATION IN SOLVER Invoke Solver by clicking Tools|Solver § Specify Target Cell (D 6) § Specify Changing Cells (highlight B 5, C 5)
ENTERING INFORMATION IN SOLVER Invoke Solver by clicking Tools|Solver § Specify Target Cell (D 6) § Specify Changing Cells (highlight B 5, C 5)
 CONSTRAINTS Specifying Constraints § Use "Add" constraints to enter relevant cell references for LHS and RHS. § Either add constraints one at a time or add blocks of constraints having same sign (<=, >=, or =) at the same time. § Since all constraints have same <= sign one chose to highlight all LHS D 8: D 10 on left and F 8: F 10 on right with <= sign.
CONSTRAINTS Specifying Constraints § Use "Add" constraints to enter relevant cell references for LHS and RHS. § Either add constraints one at a time or add blocks of constraints having same sign (<=, >=, or =) at the same time. § Since all constraints have same <= sign one chose to highlight all LHS D 8: D 10 on left and F 8: F 10 on right with <= sign.
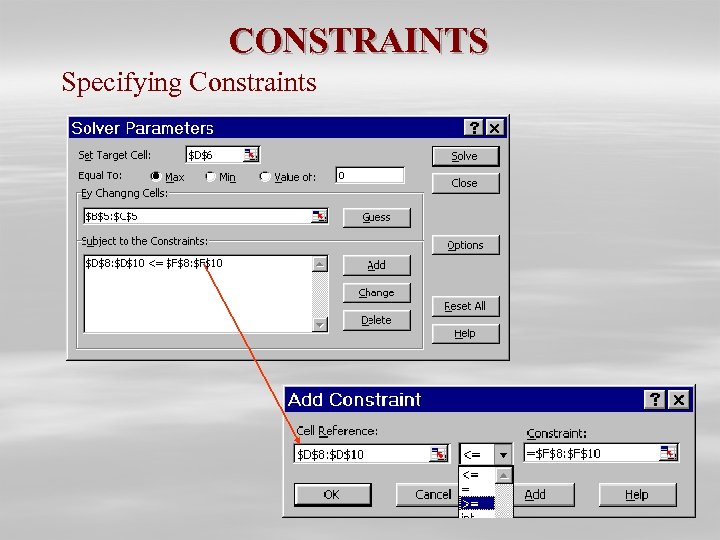 CONSTRAINTS Specifying Constraints
CONSTRAINTS Specifying Constraints
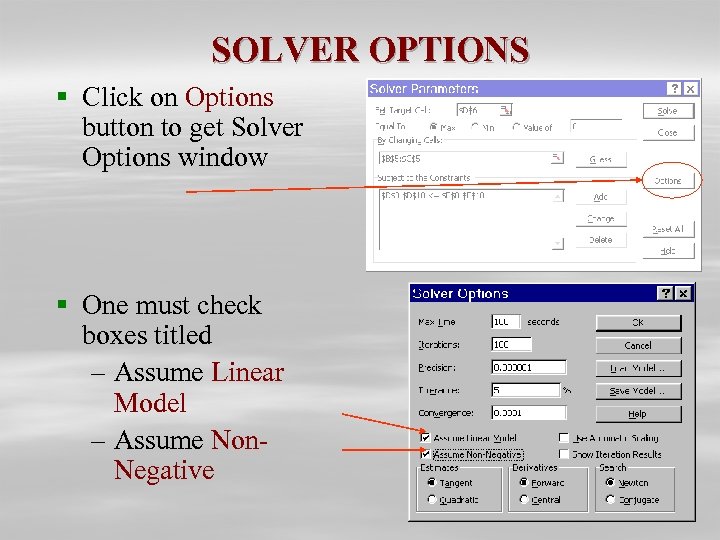 SOLVER OPTIONS § Click on Options button to get Solver Options window § One must check boxes titled – Assume Linear Model – Assume Non. Negative
SOLVER OPTIONS § Click on Options button to get Solver Options window § One must check boxes titled – Assume Linear Model – Assume Non. Negative
 SOLVING MODEL When Solve button is clicked, Solver executes model and results appear as shown. Solver Results window also indicates the availability of three reports – - Answer. - Sensitivity. - Limits.
SOLVING MODEL When Solve button is clicked, Solver executes model and results appear as shown. Solver Results window also indicates the availability of three reports – - Answer. - Sensitivity. - Limits.
 SOLUTION Optimal solution indicated that one should make 30 Tables and 40 chairs with an optimal profit of $ 410.
SOLUTION Optimal solution indicated that one should make 30 Tables and 40 chairs with an optimal profit of $ 410.
 POSSIBLE MESSAGES IN RESULTS WINDOW
POSSIBLE MESSAGES IN RESULTS WINDOW
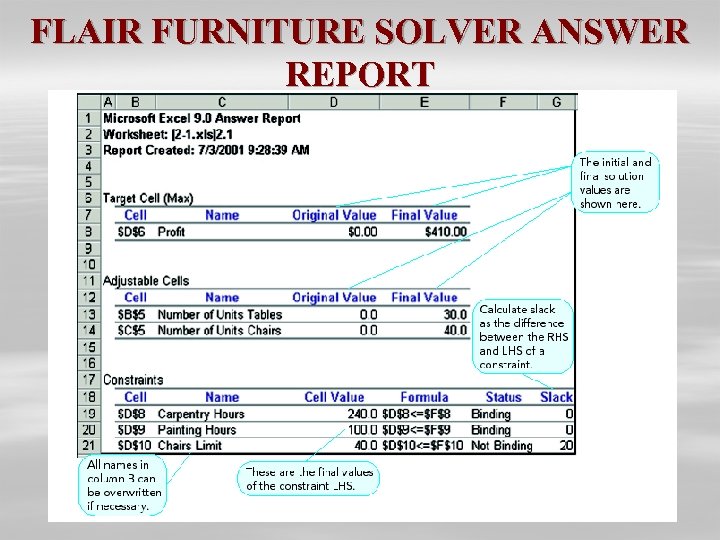 FLAIR FURNITURE SOLVER ANSWER REPORT
FLAIR FURNITURE SOLVER ANSWER REPORT
 USING SOLVER TO SOLVE HOLIDAY MEAL CHICKEN RANCH PROBLEM LP formulation for this problem is as follows: Minimize cost (in cents) = 2 A + 3 B subject to constraints 5 A + 10 B 90 (protein constraint) 4 A + 3 B 48 (vitamin constraint) ½A 1½ (iron constraint) A, B 0 (nonnegativity)
USING SOLVER TO SOLVE HOLIDAY MEAL CHICKEN RANCH PROBLEM LP formulation for this problem is as follows: Minimize cost (in cents) = 2 A + 3 B subject to constraints 5 A + 10 B 90 (protein constraint) 4 A + 3 B 48 (vitamin constraint) ½A 1½ (iron constraint) A, B 0 (nonnegativity)
 HOLIDAY MEAL CHICKEN RANCH PROBLEM SPREADSHEET
HOLIDAY MEAL CHICKEN RANCH PROBLEM SPREADSHEET
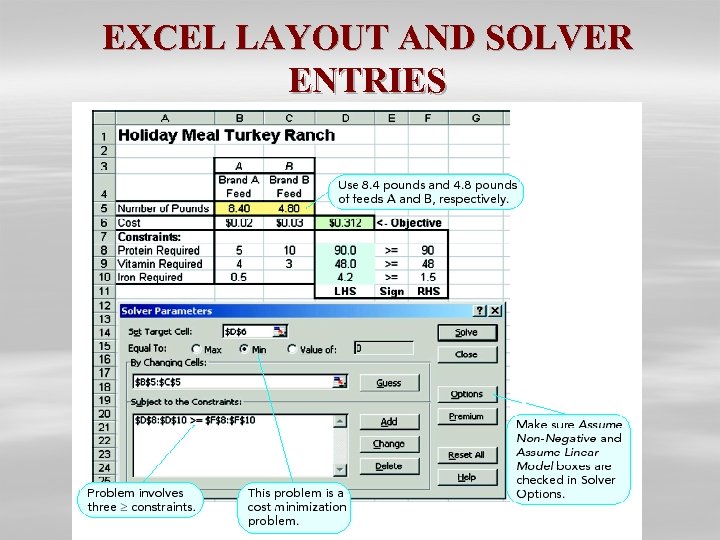 EXCEL LAYOUT AND SOLVER ENTRIES
EXCEL LAYOUT AND SOLVER ENTRIES
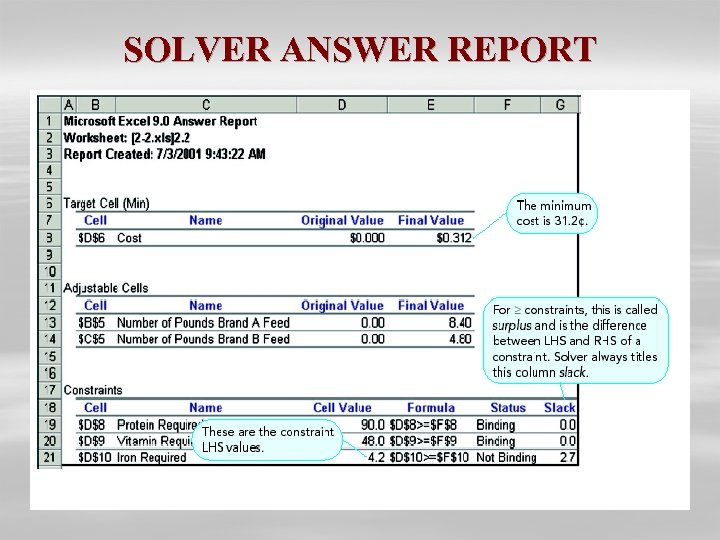 SOLVER ANSWER REPORT
SOLVER ANSWER REPORT
 SUMMARY Ø A mathematical modeling technique called linear programming (LP) is introduced Ø LP models are used to find an optimal solution to problems that have a series of constraints binding the objective value. Ø How models with only two decision variables can be solved graphically is shown Ø To solve LP models with numerous decision variables and constraints, one need a solution procedure such as simplex algorithm. Ø How LP models can be set up on Excel and solved using Solver is demonstrated
SUMMARY Ø A mathematical modeling technique called linear programming (LP) is introduced Ø LP models are used to find an optimal solution to problems that have a series of constraints binding the objective value. Ø How models with only two decision variables can be solved graphically is shown Ø To solve LP models with numerous decision variables and constraints, one need a solution procedure such as simplex algorithm. Ø How LP models can be set up on Excel and solved using Solver is demonstrated


