Linear Programming Pens and Pencils A

Linear Programming

Pens and Pencils § A boy buys x pencils and y pens. Pencils cost 10 pence each and pens cost 20 pence.

On your whiteboards § Write an expression for the total cost of x pencils at 10 pence each. § Write an expression for the total cost of y pens at 20 pence each.

Pens and Pencils § Pencils cost 10 pence each and pens cost 20 pence. The boy has £ 1. 50 to spend. He must buy at least 4 pencils and at least 1 pen.

On your whiteboards… § Write an inequality for… – “He must buy at least 4 pencils” – “He must buy at least 1 pen” – “Pencils cost 10 pence each and pens cost 20 pence each. He has £ 1. 50 to spend. ”

What did you get? § “He must buy at least 4 pencils” x≥ 4 § “He must buy at least 1 pen” y≥ 1 § “Pencils cost 10 pence each and pens cost 20 pence each. He has £ 1. 50 to spend. ” 10 x + 20 y ≤ 150

Can you simplify? 10 x + 20 y ≤ 150 Can you write this in a simpler way? x + 2 y ≤ 15

On your grids… § Draw a diagram to show the region defined by these three inequalities: x≥ 4 y≥ 1 x + 2 y ≤ 15 § REMEMBER TO SHADE THE REGION YOU DON’T WANT!

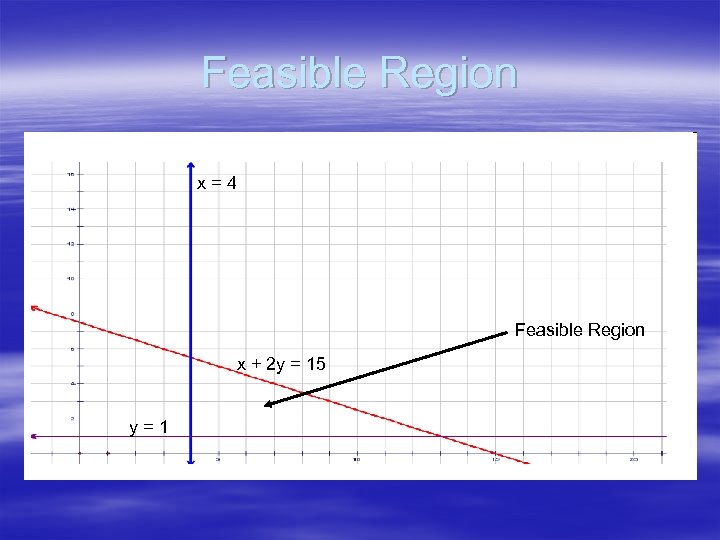Feasible Region x=4 Feasible Region x + 2 y = 15 y=1

Objective Function § Find the maximum number of pens and pencils the boy can buy. 14!

On your whiteboards § If the boy sells pencils for 20 pence and pens for 25 pence write an expression for his profit. 10 x + 5 y § Use your graph to find the maximum profit the boy can make.

How much money? £ 1. 35 (13 pencils and 1 pen)