Linear Collider Parameters International Linear Collider School May

Linear Collider Parameters International Linear Collider School May 21 st, 2006 Tor Raubenheimer

Outline • Luminosity and beam parameters – Introduction – Luminosity expressions – IP parameters • Beamstrahlung • Disruption • Spot size limitations – Particle sources – Emittance generation • Damping rings, bunch compression, and Linac emittance limits – Final focusing system – RF system parameters and efficiency to be covered by Chris Adolphsen

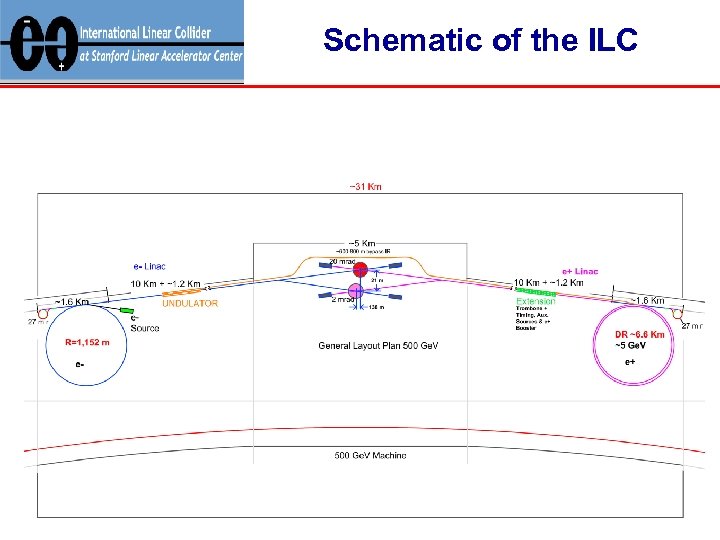
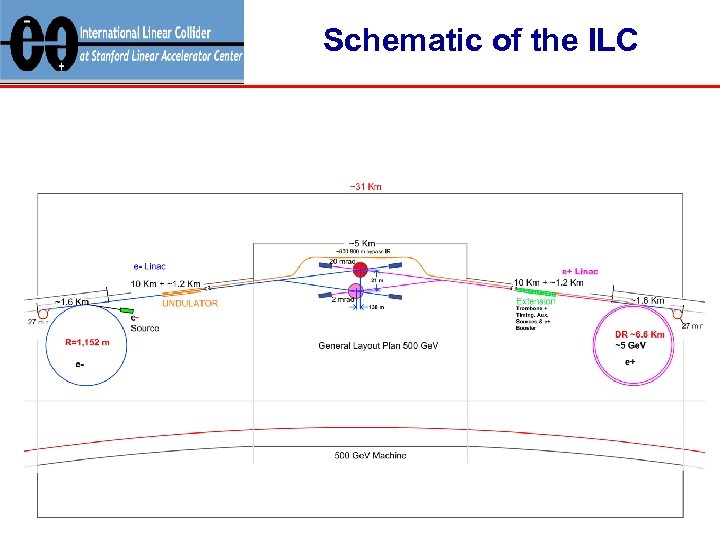Schematic of the ILC

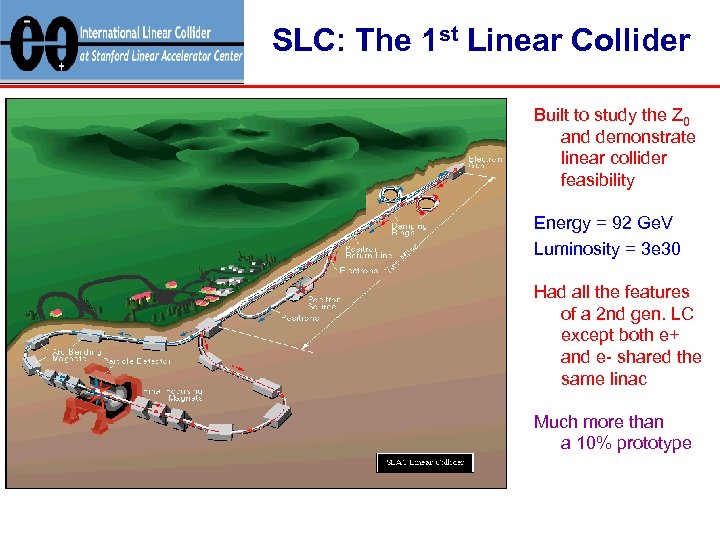SLC: The 1 st Linear Collider Built to study the Z 0 and demonstrate linear collider feasibility Energy = 92 Ge. V Luminosity = 3 e 30 Had all the features of a 2 nd gen. LC except both e+ and e- shared the same linac Much more than a 10% prototype

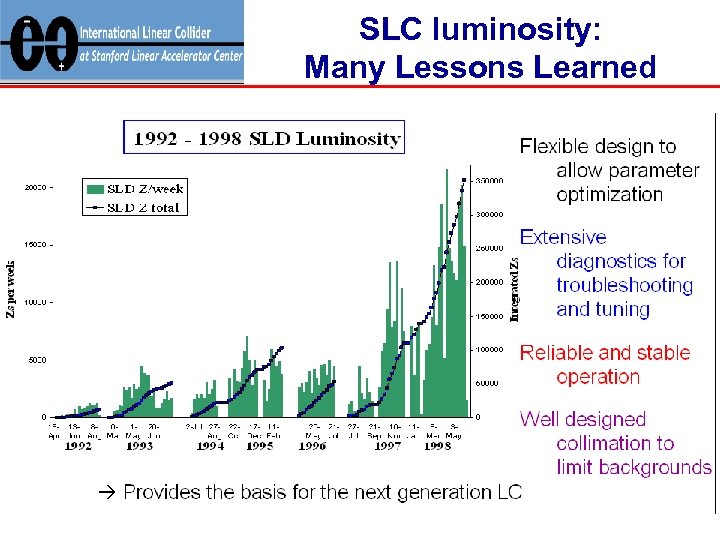SLC luminosity: Many Lessons Learned

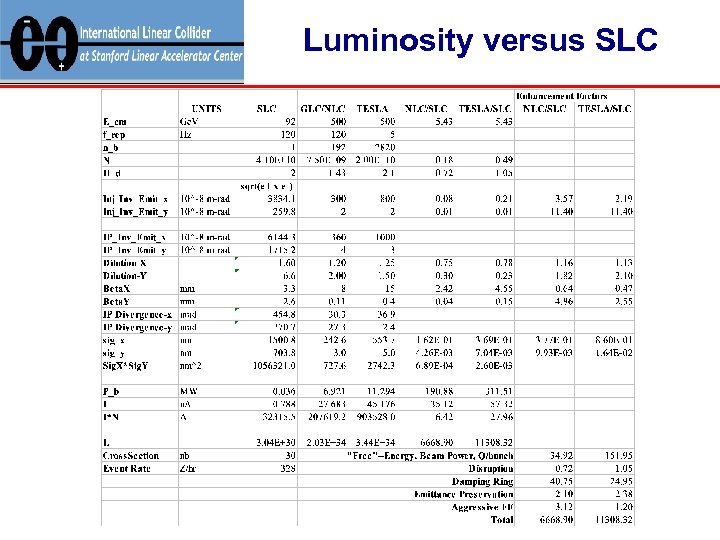Luminosity versus SLC

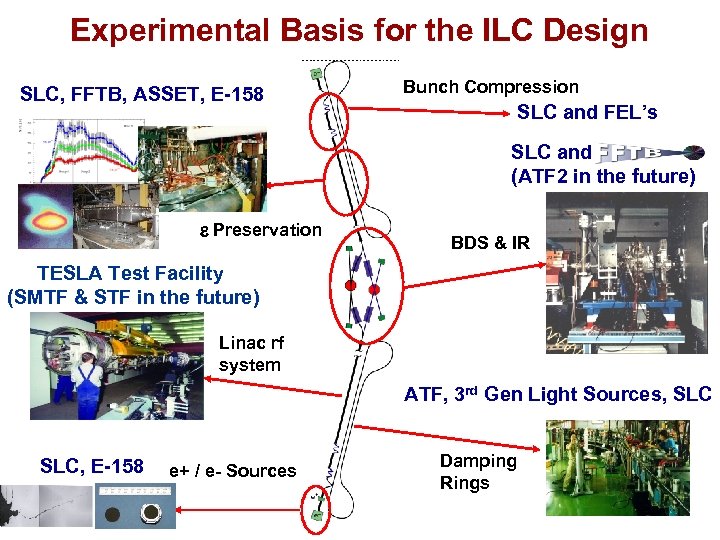Experimental Basis for the ILC Design SLC, FFTB, ASSET, E-158 Bunch Compression SLC and FEL’s SLC and (ATF 2 in the future) e Preservation BDS & IR TESLA Test Facility (SMTF & STF in the future) Linac rf system ATF, 3 rd Gen Light Sources, SLC, E-158 e+ / e- Sources Damping Rings

Luminosity: Aiming for 2 x 1034 Collider luminosity (cm-2 s-1) is approximately given by where: nb = bunches / train N = particles per bunch frep = repetition frequency A = beam cross-section at IP HD = beam-beam enhancement factor For a Gaussian beam distribution where Sx = sqrt(sx 12 + sx 22):

Luminosity • frep * nb tends to be low in a linear collider • Fortunately the beam-beam tune shift limit is much looser in a linear collider than a storage rings achieve luminosity with spot size and bunch charge – Small spots mean small emittances and small betas: sx = sqrt(bx ex)

Interjection – Phase Space Beta function b characterize optics Emittance e is phase space volume of the beam – optics analogy is the wavelength Tilt is parameterized with a Beam size: (e b)1/2 Divergence: (e /b)1/2 Squeeze on beam size increase angular divergence Beam emittance is not conserved during acceleration normalized emittance should be ge

Linear Collider Luminosity • Convert luminosity expression using beam power – Pbeam = Ecms * e. N * nb * frep – Required to have large beam powers • Further constrained by IP effects – Beamstrahlung – synchrotron radiation due to strong beam fields – Disruption – beam distortion due to strong beam fields at the IP – Hourglass – b ≥ sz • For flat beams (sx >> sy) where d ~ N 2/sx 2 sz

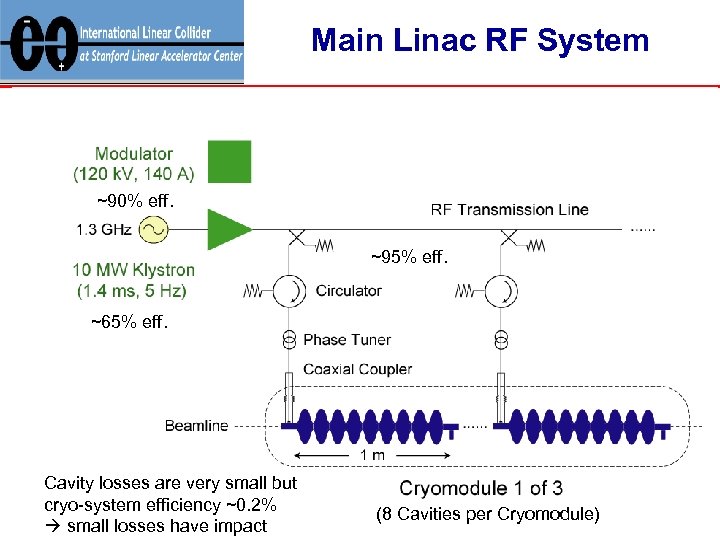Main Linac RF System ~90% eff. ~95% eff. ~65% eff. Cavity losses are very small but cryo-system efficiency ~0. 2% small losses have impact (8 Cavities per Cryomodule)

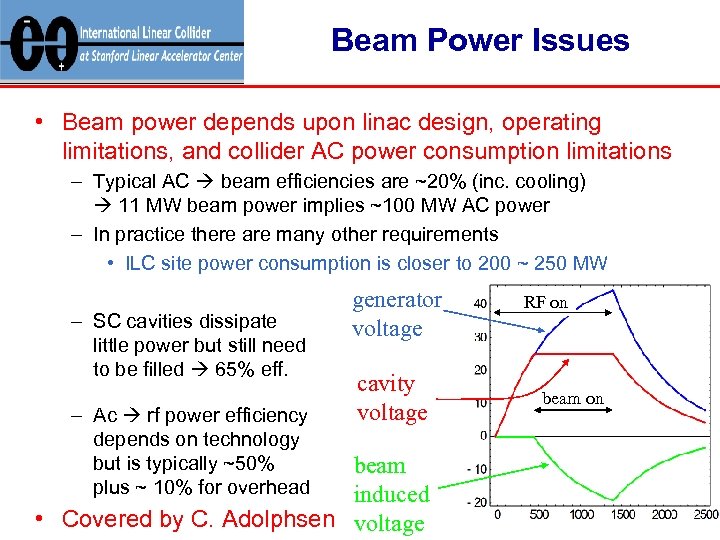Beam Power Issues • Beam power depends upon linac design, operating limitations, and collider AC power consumption limitations – Typical AC beam efficiencies are ~20% (inc. cooling) 11 MW beam power implies ~100 MW AC power – In practice there are many other requirements • ILC site power consumption is closer to 200 ~ 250 MW – SC cavities dissipate little power but still need to be filled 65% eff. – Ac rf power efficiency depends on technology but is typically ~50% plus ~ 10% for overhead generator voltage cavity voltage beam induced • Covered by C. Adolphsen voltage RF on beam on

Beam Parameters • Requirements: – High luminosity – set by physics needs – Low backgrounds (small IP effects) – Forced to high beam power and small vertical spots • Details of technology determine other limitations – – – Rf cavities and power sources 10 m. A beam current Damping rings beam emittances and number of bunches Bunch compressors IP bunch length Cryogenic systems duty cycle Extensive cost optimization is required to balance systems • Linear collider will push many technological and beamphysics limits – Need to have operational flexibility to overcome unexpected problems

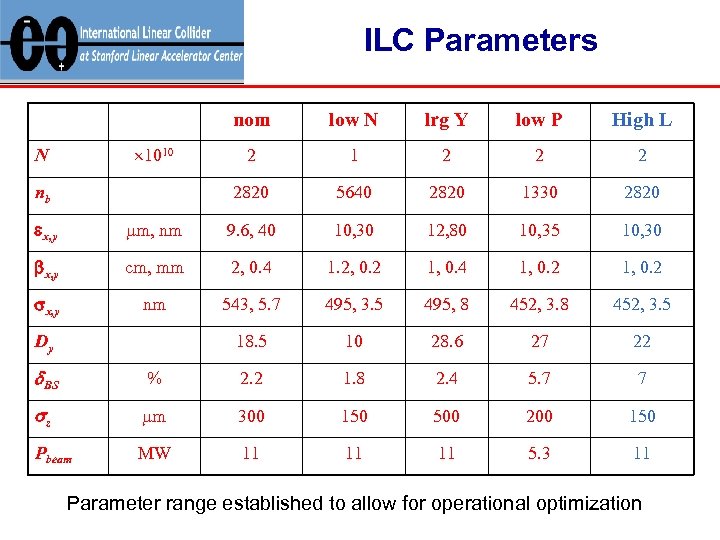
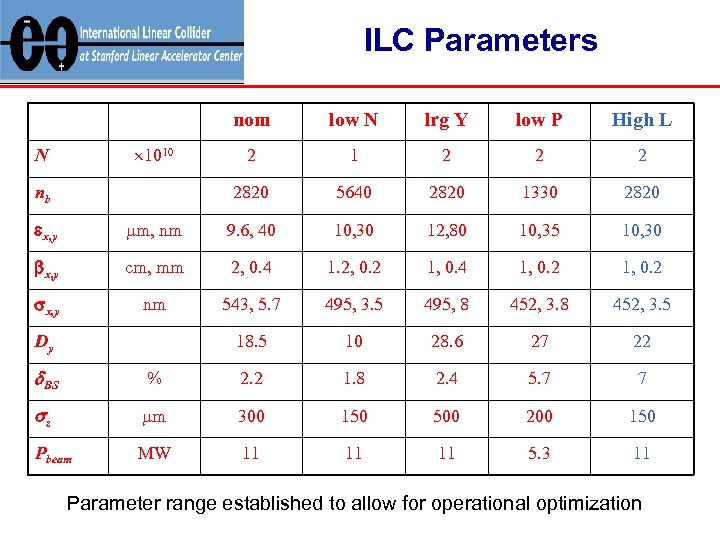ILC Parameters nom nb lrg Y low P High L 2 1 2 2820 1010 N low N 5640 2820 1330 2820 ex, y mm, nm 9. 6, 40 10, 30 12, 80 10, 35 10, 30 bx, y cm, mm 2, 0. 4 1. 2, 0. 2 1, 0. 4 1, 0. 2 sx, y nm 543, 5. 7 495, 3. 5 495, 8 452, 3. 5 18. 5 10 28. 6 27 22 Dy d. BS % 2. 2 1. 8 2. 4 5. 7 7 sz mm 300 150 500 200 150 Pbeam MW 11 11 11 5. 3 11 Parameter range established to allow for operational optimization

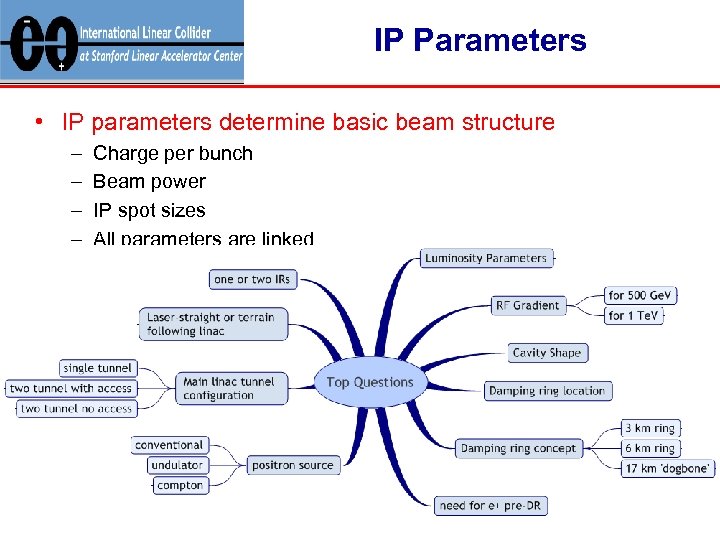IP Parameters • IP parameters determine basic beam structure – – Charge per bunch Beam power IP spot sizes All parameters are linked

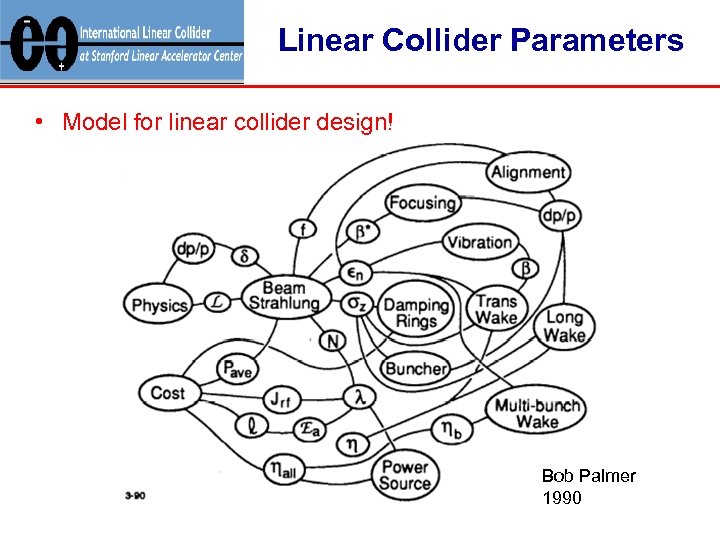Linear Collider Parameters • Model for linear collider design! Bob Palmer 1990

Beam-Beam Tune Shifts • Fields from charge particles focus (or defocus) each other as they pass through each other in IP – Effect is known as the beam-beam tune shift in a storage ring xx, y and is typically limited to ~ 0. 05 to prevent the beam spot sizes from increasing as the beam circulates • In ILC, the ‘ring tune shift’ is ~2 (thin lens calculation) • Ideally in single-pass collider the tune-shift is not a limitation – In practice it is still a limit but is much looser – The analogous effect is referred to as the disruption in an LC

IP Beam Fields (1) • Fields from charge particles focus (or defocus) each other as they pass through each other in IP • Fields from relativistic beam are radial – spread as 1/g: v~c a linear charge density = l

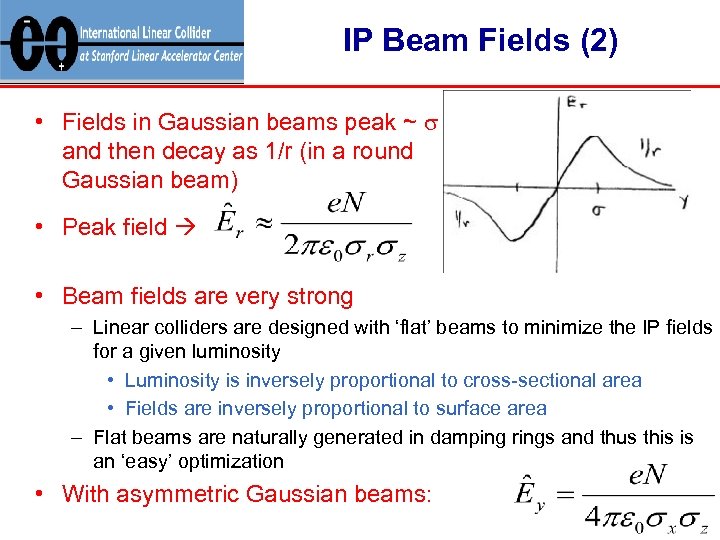IP Beam Fields (2) • Fields in Gaussian beams peak ~ s and then decay as 1/r (in a round Gaussian beam) • Peak field • Beam fields are very strong – Linear colliders are designed with ‘flat’ beams to minimize the IP fields for a given luminosity • Luminosity is inversely proportional to cross-sectional area • Fields are inversely proportional to surface area – Flat beams are naturally generated in damping rings and thus this is an ‘easy’ optimization • With asymmetric Gaussian beams:

IP Beam Fields (3) • F = e(Er + c. Bq) – E and B cancel at as 1/g 2 in co-propagating – E and B add in counter-propagating beams F ~ 2 e. Er • Fields are extremely strong at IP ~ few V / Angstrom or k. T [kilo-Tesla] • Main effects: beam disruption and synchrotron radiation • Focusing at IP is given by d. F / dr normalize by charge and mass K [m-2] • Now: • Finally with asymmetric Gaussian beams: a 2 2 sx, y(sx + sy)

IP Beam Fields • Two main effects: – Beamstrahlung – Synchrotron radiation of particles in the strong fields of the opposing beam; many % of the beam energy can be radiated • Pair production – Intense fields can convert beamstrahlung photons into e+/e- pairs – Disruption – fields of the opposing beam will distort the beam during the collision • Pinch effect luminosity enhancement where mutual focusing of the oppositely charged beams increases density in collision • Beam-beam deflections small offsets between the beam are amplified into large angular kicks which can be measures and used to stabilize the collision • Single bunch kink when disruption is large enough, end up with a two-stream instability which can reduce luminosity

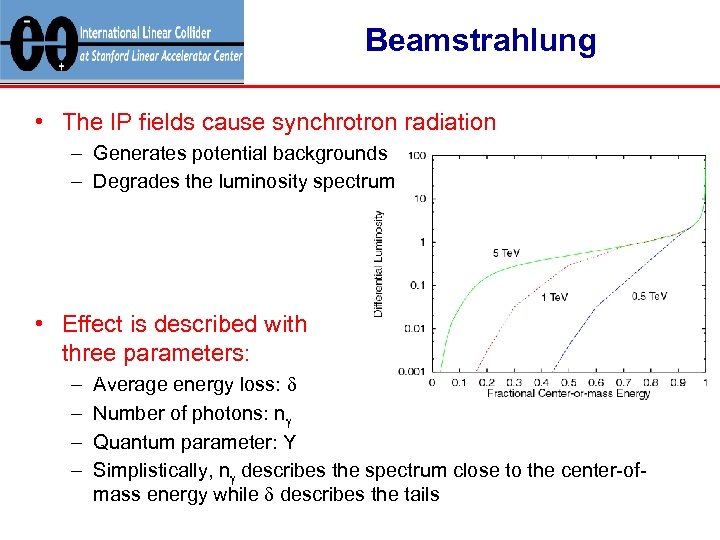Beamstrahlung • The IP fields cause synchrotron radiation – Generates potential backgrounds – Degrades the luminosity spectrum • Effect is described with three parameters: – – Average energy loss: d Number of photons: ng Quantum parameter: Y Simplistically, ng describes the spectrum close to the center-ofmass energy while d describes the tails

Simple Beamstrahlung • Beam particles radiate synchrotron radiation in strong fields where • For nominal ILC parameters at 250 Ge. V and using the peak B field ~60 Ge. V radiated in collision or 25% of energy – Need to do the calculation properly averaging over the beam but scaling is clear USR ~ g 2 sz N 2 / sx 2

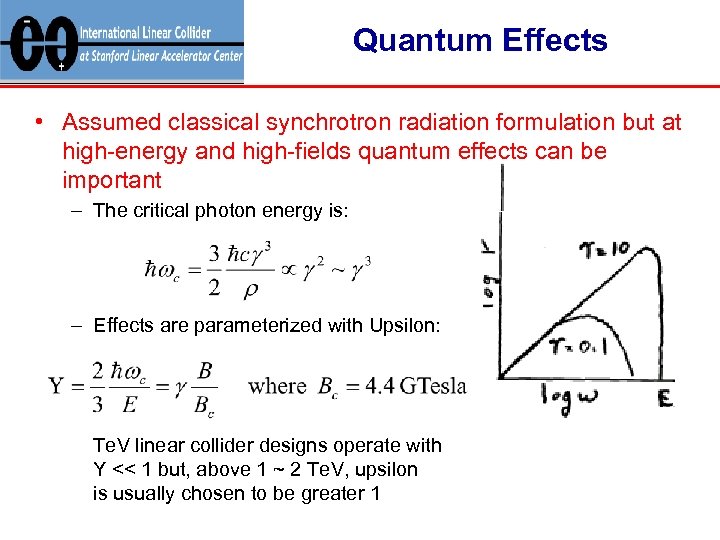Quantum Effects • Assumed classical synchrotron radiation formulation but at high-energy and high-fields quantum effects can be important – The critical photon energy is: – Effects are parameterized with Upsilon: Te. V linear collider designs operate with Y << 1 but, above 1 ~ 2 Te. V, upsilon is usually chosen to be greater 1

Beamstrahlung Formula • Approximate formulas can be written which describe the process over the usual range of LC parameters • See: P. Chen, “Differential Luminosity under Multi-Photon Beamstrahlung”, Phys. Rev. D, 46: 1186 (1992). K. Yokoya, P. Chen, “Beam-beam phenomena in linear colliders, ” Lecture Notes Physics, 400: 415 (1992). P. Chen, “Disruption effects from the collision of quasi-flat beams, ” PAC 93.

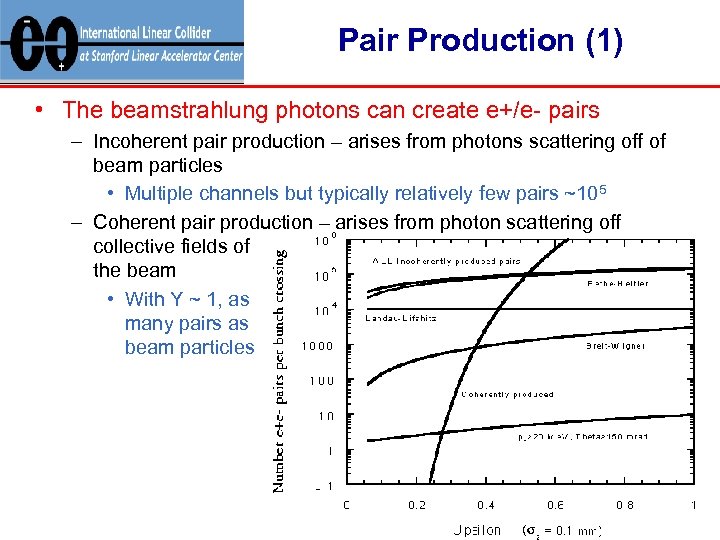Pair Production (1) • The beamstrahlung photons can create e+/e- pairs – Incoherent pair production – arises from photons scattering off of beam particles • Multiple channels but typically relatively few pairs ~105 – Coherent pair production – arises from photon scattering off collective fields of the beam • With Y ~ 1, as many pairs as beam particles

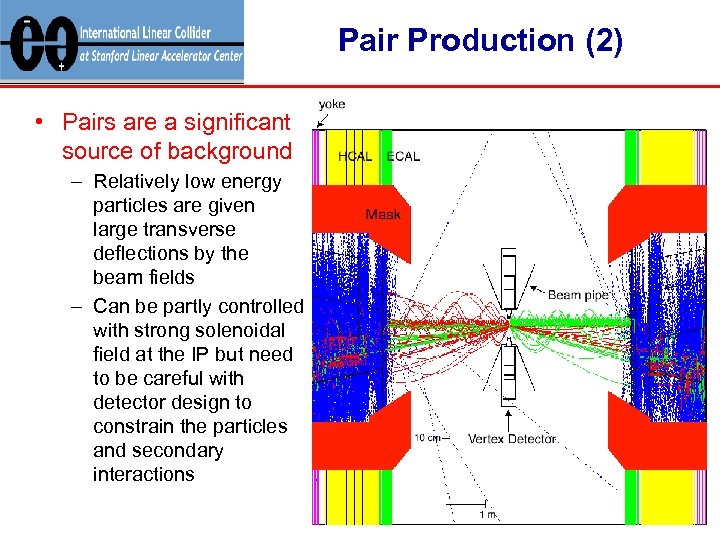Pair Production (2) • Pairs are a significant source of background – Relatively low energy particles are given large transverse deflections by the beam fields – Can be partly controlled with strong solenoidal field at the IP but need to be careful with detector design to constrain the particles and secondary interactions

Disruption (1) • Strong fields will distort the opposing beam • Normalized beam-beam focusing force at the IP: • Disruption parameter defined using thin lens approximation and comparing focal to bunch length • Assume a rectangular distribution number of oscillations in opposing bunch:

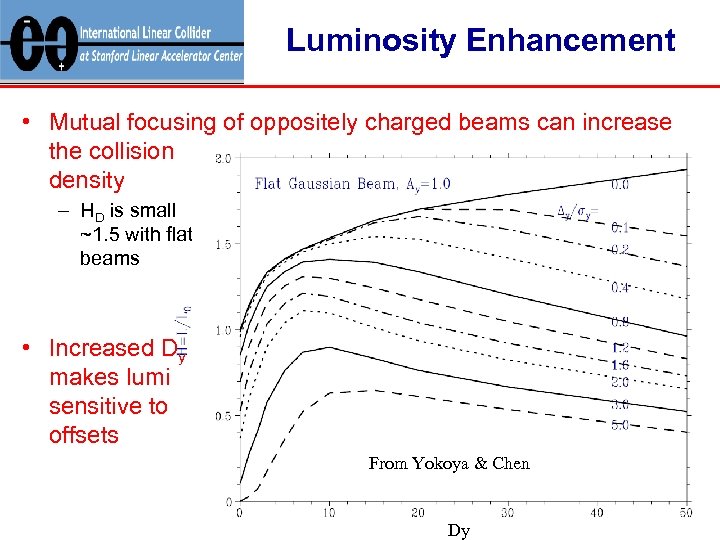Luminosity Enhancement • Mutual focusing of oppositely charged beams can increase the collision density – HD is small ~1. 5 with flat beams • Increased Dy makes lumi sensitive to offsets From Yokoya & Chen Dy

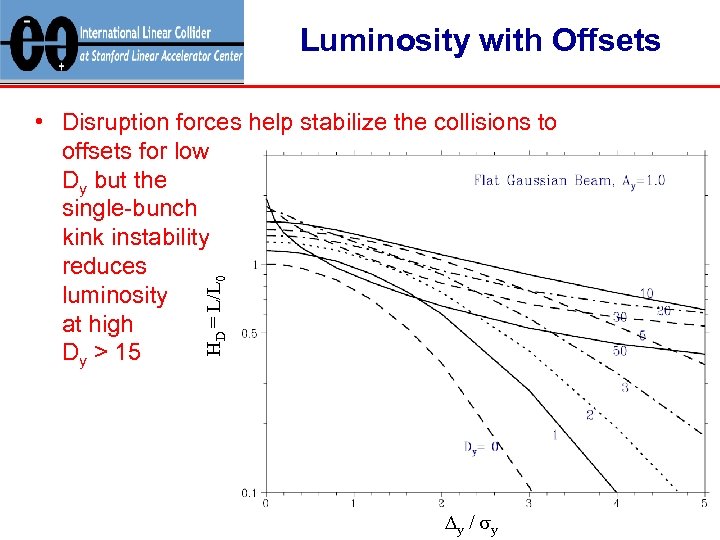Luminosity with Offsets HD = L/L 0 • Disruption forces help stabilize the collisions to offsets for low Dy but the single-bunch kink instability reduces luminosity at high Dy > 15 D y / sy

Luminosity Enhancement • Many simulations have been written to model IP environment: – CAIN – Yokoya and Chen – Guinea. Pig – Shulte • An empirical expression was fit to simulation results • Depends on disruption and weakly on depth of focus (hour -glass effect) – Expression is valid over typical LC parameters – Needs to supported with detailed simulations

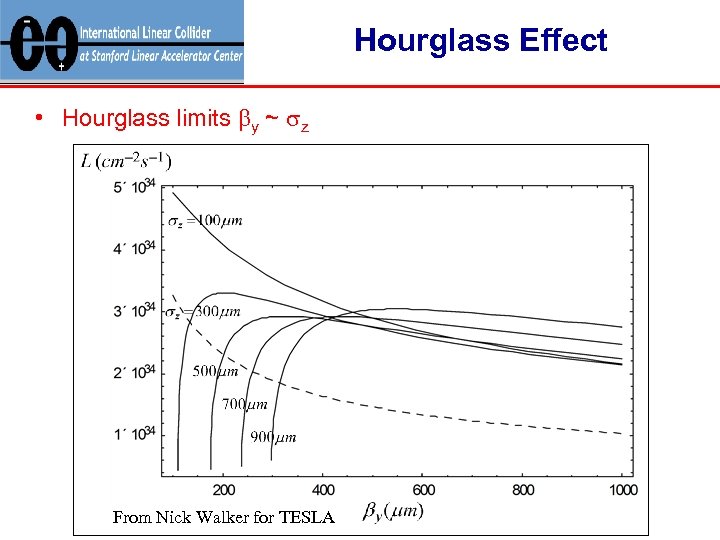Hourglass Effect • Hourglass limits by ~ sz From Nick Walker for TESLA

Single Bunch Kink (1) • Single bunch kink is a two-stream instability – Small offsets are amplified by very strong beam-beam forces • Potential limitation at high disruption parameters – Why high disruption? – Luminosity expression can be re-written in terms of Dy – If there is a practical limit on the maximum disruption luminosity can be increased by shortening the bunch – Hard to avoid larger beamstrahlung

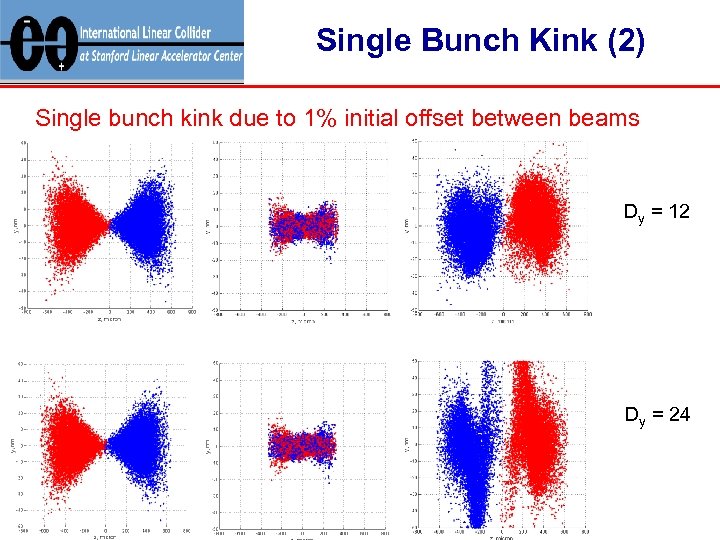Single Bunch Kink (2) Single bunch kink due to 1% initial offset between beams Dy = 12 Dy = 24

Single Bunch Kink Movie

ILC Parameters nom nb lrg Y low P High L 2 1 2 2820 1010 N low N 5640 2820 1330 2820 ex, y mm, nm 9. 6, 40 10, 30 12, 80 10, 35 10, 30 bx, y cm, mm 2, 0. 4 1. 2, 0. 2 1, 0. 4 1, 0. 2 sx, y nm 543, 5. 7 495, 3. 5 495, 8 452, 3. 5 18. 5 10 28. 6 27 22 Dy d. BS % 2. 2 1. 8 2. 4 5. 7 7 sz mm 300 150 500 200 150 Pbeam MW 11 11 11 5. 3 11 Parameter range established to allow for operational optimization

Schematic of the ILC

Polarized Electron Source • Polarized electron beam generated from a polarized laser on a strained Ga. As photocathode • Technology is robust – Demonstrated for years on SLC and E-158 at SLAC – Laser system has new requirements but is not thought to be a significant technical limitation • Options for new technology in the form of polarized rf guns – Requires more robust photocathode material – Gains in operational simplicity but not large cost savings UNLESS the rf gun can replace the damping rings – Damping rings have multiple functions • Damp incoming phase space • Provide a stable platform and damping incoming transients • Allow for feed-forward to pre-set linac systems

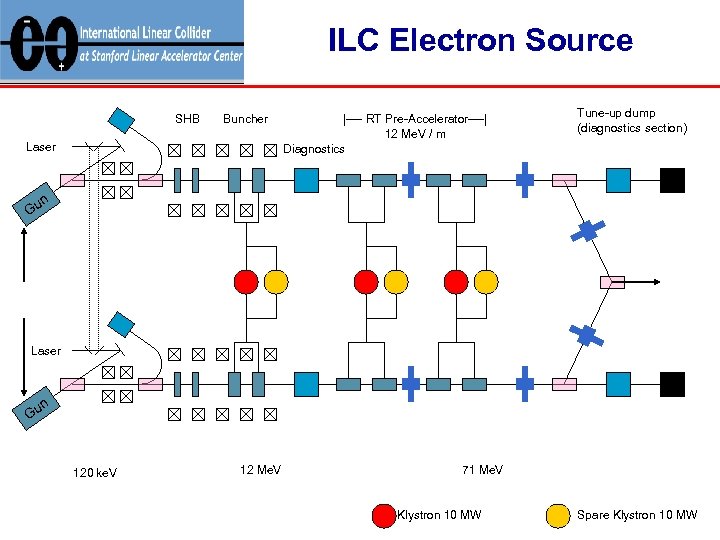ILC Electron Source SHB Buncher Laser |---- RT Pre-Accelerator----| 12 Me. V / m Diagnostics Tune-up dump (diagnostics section) n Gu Laser n Gu 120 ke. V 12 Me. V 71 Me. V Klystron 10 MW Spare Klystron 10 MW

Polarized Photo-cathodes

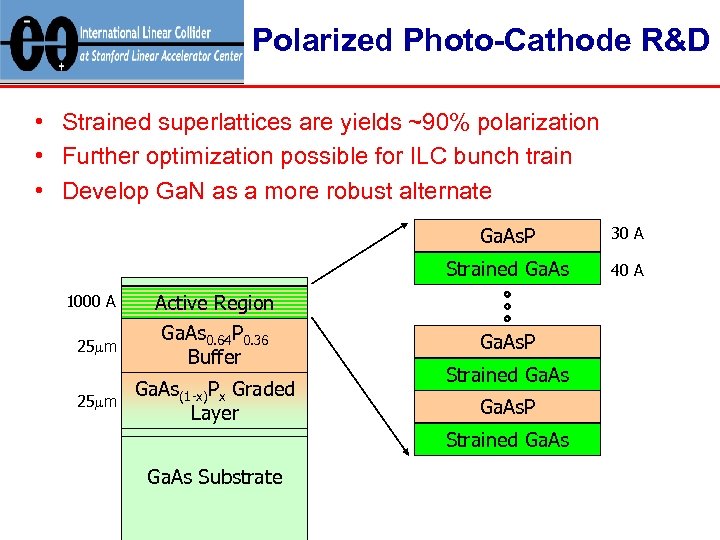Polarized Photo-Cathode R&D • Strained superlattices are yields ~90% polarization • Further optimization possible for ILC bunch train • Develop Ga. N as a more robust alternate Ga. As. P Strained Ga. As 1000 A 25 mm Active Region Ga. As 0. 64 P 0. 36 Buffer Ga. As(1 -x)Px Graded Layer 30 A 40 A Ga. As. P Strained Ga. As Substrate

Positron Source • Large number of positrons required per second – – 60 times more than in SLC Pulsed damage to the target Average heating of the target Radiation damping to the target • Difficult complex system SLC e+ target Beam direction

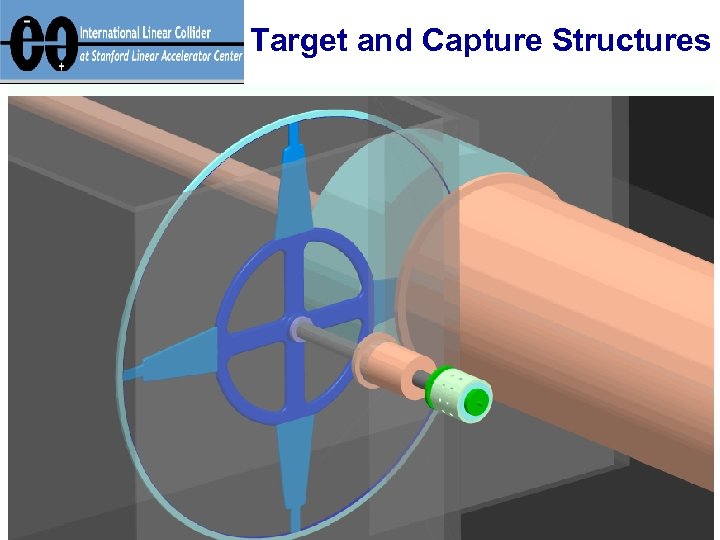Target and Capture Structures

ILC Positron Source • Three options considered for ILC – Thick 4 rl WRe target with ~6 Ge. V e- beam • Conventional technology but very high radiation loads – Thin Ti target with 10 Me. V photon beam • Photon beam generated by passing 150 Ge. V e- thru undulator • Allows for e+ polarization as well – Thin target using Compton scattered laser beam • Requires very powerful laser systems but would have benefits of independence from e- beam and possible polarization • Capture systems are the same in all cases – Chose undulator-based source as baseline – Many advantages – only problem is that it couples e+ source to the electron beam and constrains timing systems and beam operations

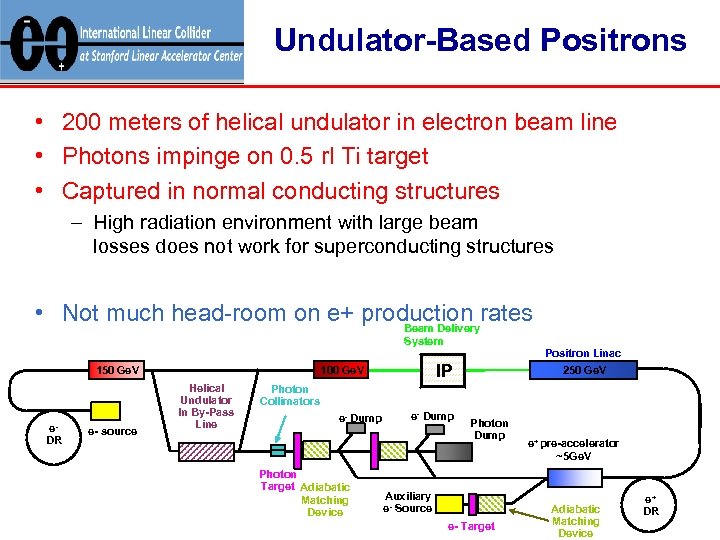Undulator-Based Positrons • 200 meters of helical undulator in electron beam line • Photons impinge on 0. 5 rl Ti target • Captured in normal conducting structures – High radiation environment with large beam losses does not work for superconducting structures • Not much head-room on e+ production rates Beam Delivery System 150 Ge. V e. DR e- source IP 100 Ge. V Helical Undulator In By-Pass Line Positron Linac 250 Ge. V Photon Collimators e- Dump Photon Target Adiabatic Matching Device e- Dump Photon Dump Auxiliary e- Source e- Target e+ pre-accelerator ~5 Ge. V Adiabatic Matching Device e+ DR

Damping Rings • Damping rings have more accelerator physics than the rest of the collider • Required to: 1. Damp beam emittances and incoming transients 2. Provide a stable platform for downstream systems 3. Have excellent availability ~99% (best of 3 rd generation SRS) • Mixed experience with SLC damping rings: – Referred to as the “The source of all Evil” – Collective instabilities; Dynamic aperture; Stability • Damping ring designs based on KEK ATF, 3 rd generation SRS, and high luminosity factories – Experimental results provide confidence in design

KEK ATF Damping Ring • Probably world’s largest linear collider test facility World’s lowest emittance beam: ey = 4 pm-rad below X-band LC requirements Used to verify X-band DR concepts Detailed measurements of emittance tuning, lattice properties, IBS, ions, collective effects, and instrumentation 1. 3 Ge. V Damping Ring and S-band linac Commissioning started in 1997

Damping Ring Emittances (1) • See M. Sand, “Physics of Electron Storage Rings, ” SLAC 121 (1972). • Two competing processes: radiation damping and quantum excitation • Radiation damping: – Longitudinal phase space • Higher energy particles radiate more energy than low energy particles in the bends – Transverse phase space • Radiation is emitted in a narrow cone centered on the instantaneous direction of motion – Transverse momentum is radiated away • Energy is restored by the RF cavities longitudinally • Combined effect of radiation and RF is a loss in transverse momentum

Damping Ring Emittances (2) • Quantum excitation – Radiation is emitted in discrete quanta – Number and energy distribution etc. of photons obey statistical laws – Radiation process can be modeled as a series of “kicks” that excite longitudinal and transverse oscillations Nominal Trajectory DE = 0 Low E Trajectory Start to oscillate about nominal trajectory

Damping Ring Emittances (3) • Quantum excitation occurs in the horizontal plane • Two effects determine the vertical emittance: – Opening angle of the SR – typically limits at about 10% of design emittance – Alignment errors which couple the horizontal to the vertical • Vertical bending due to orbit errors • Skew quadrupole fields due to quadrupole rotations or vertical sextupole misalignments • Tolerances are very tight – frequently a few microns • Combined effect of radiation damping and excitation: einj = injected emittance eequ = equilibrium emittance t = radiation damping time

Issues in the Damping Rings • Emittance tuning and error correction – Orbit correction and component stabilization • Injection/extraction of individual bunches – Kicker rise/fall time – very large rings to store 3000 bunches • Dynamic aperture – Long wigglers needed if the ring is too big • Single-bunch intensity – Tune shift by self-Coulomb force (space charge) • Instabilities (mainly average current) – Electron cloud instability – Fast ion instability – Classical collective instabilities • Rings operate in a new regime with fast damping and very small beam emittances

Bunch Compressors • Bunch lengths in damping rings are ~1 cm – Seen that for high luminosity, would like short bunches at the IP • Compress bunches in magnetic bunch compressors after the damping rings – Three problems: • Magnetic bunch compressors operate by bending the beam synchrotron radiation can dilute the beam emittances – Normalized emittance growth scales as g 6 in transport line • Longitudinal phase space is conserved shortening the bunch length will increase the energy spread – Large energy spread in the linacs makes preserving the beam emittance more difficult De ~ (DE/E)2 • Longitudinal nonlinearities make compressing by more than 10~20 x difficult in any single stage

Bunch Compressors Magnetic bunch compression DE/E Overcompressi on 2 sz 0 z z Undercompressio n z 2 sz V = V 0 sin(wt) RF Accelerating Voltage Dz = R 56 DE/E Path Length-Energy Dependent Beamline

ILC BC Solution • Want capability of compressing from 6 mm 150 mm • Factor of 40 too large for a simple single-stage system – Dual stage system: • Compress just after damping ring at 5 Ge. V by ~6 x • Compress again at ~15 Ge. V point by another factor of ~8 x • Provides large operating range while limiting the energy spread in the linacs less emittance dilution than in a single-stage • Bunch compressor system also includes: – Transverse and longitudinal collimation – Spin rotation – Skew correction to correct errors from damping ring or in the spin rotation system – Extensive diagnostics before launching the beam into the linac

Linac Beam Dynamics • Main issues in the linac are: – Short-range wakefields – Dispersive emittance dilutions • Superconducting linac has relatively loose tolerances for wakefield dilutions – Cavity alignment at the 300 mm level • Need to be careful on alignment at the low energy ends of the linac due to the dispersive dilutions – Must align the quadrupoles at the 25 mm level to avoid dispersive dilutions: De ~ (DE/E)2 – Requires beam-based alignment techniques

Linac Parameter Trades Linac (relaxed within limits) Damping Ring (sources) IR (IP) Beam extraction From Nick Walker, Snowmass 2005

Beam Delivery System • Requirements: – – Focus beams down to very small spot sizes Collect out-going disrupted beam and transport to the dump Collimate the incoming beams to limit beam halo Provide diagnostics and optimize the system and determine the luminosity spectrum for the detector – Switch between IPs

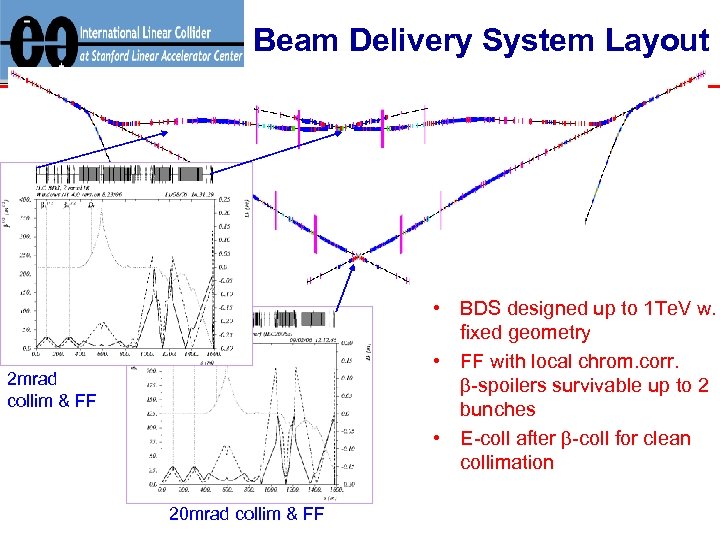Beam Delivery System Layout • BDS designed up to 1 Te. V w. fixed geometry • FF with local chrom. corr. b-spoilers survivable up to 2 bunches • E-coll after b-coll for clean collimation 2 mrad collim & FF 20 mrad collim & FF

Collimation System and MPS • Collimation system must remove beam tails • Extremely dense beams are very difficult to collimate and stop – Machine Protection System is a challenge • Collimation system becomes long and difficult with tight tolerances if the beam size is increased sufficiently to prevent damage

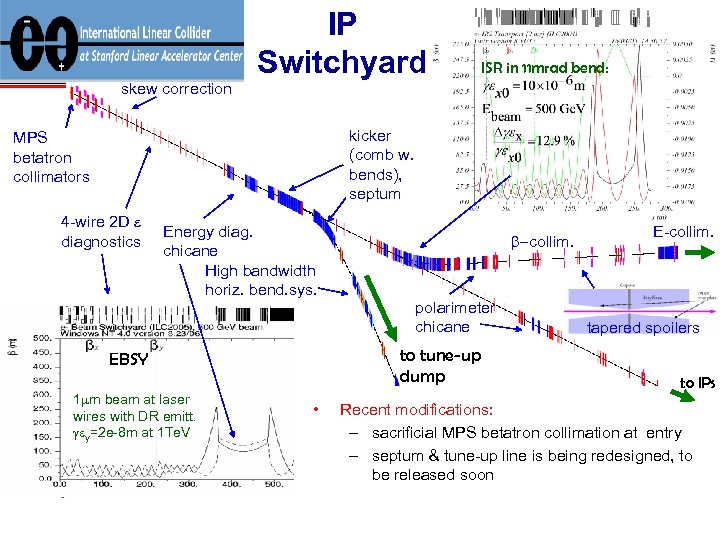IP Switchyard ISR in 11 mrad bend: skew correction kicker (comb w. bends), septum MPS betatron collimators 4 -wire 2 D e diagnostics Energy diag. chicane High bandwidth horiz. bend. sys. b-collim. polarimeter chicane to tune-up dump EBSY 1 mm beam at laser wires with DR emitt. gey=2 e-8 m at 1 Te. V • E-collim. tapered spoilers to IPs Recent modifications: – sacrificial MPS betatron collimation at entry – septum & tune-up line is being redesigned, to be released soon

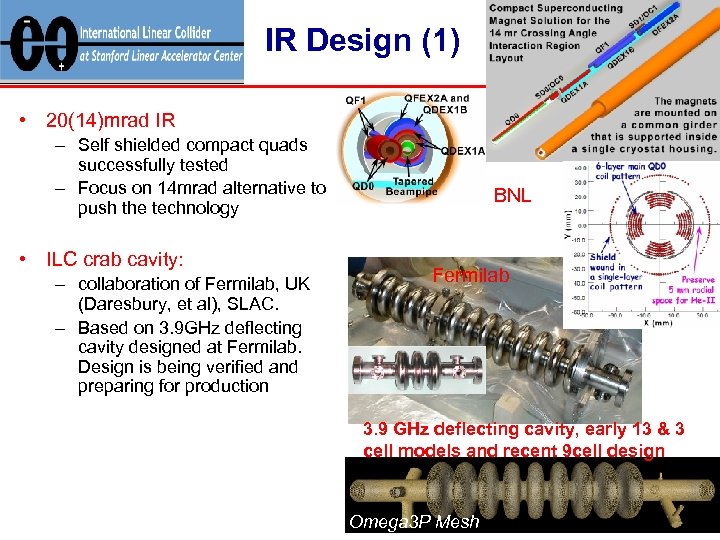IR Design (1) • 20(14)mrad IR – Self shielded compact quads successfully tested – Focus on 14 mrad alternative to push the technology • ILC crab cavity: – collaboration of Fermilab, UK (Daresbury, et al), SLAC. – Based on 3. 9 GHz deflecting cavity designed at Fermilab. Design is being verified and preparing for production BNL Fermilab 3. 9 GHz deflecting cavity, early 13 & 3 cell models and recent 9 cell design Omega 3 P Mesh

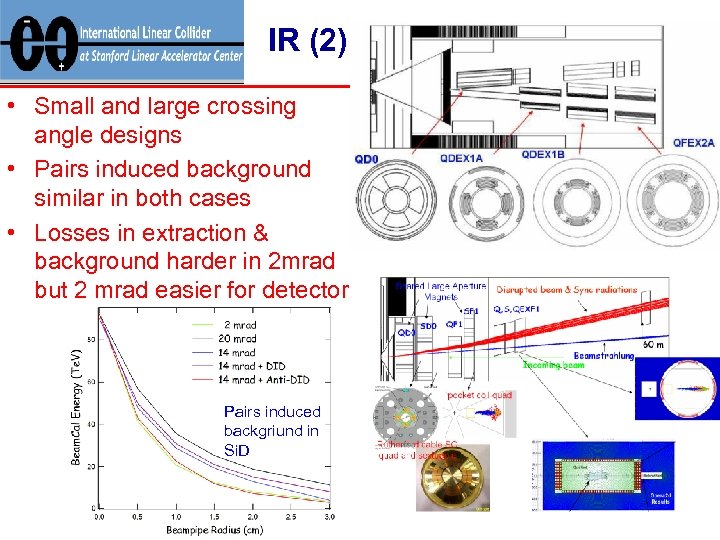IR (2) • Small and large crossing angle designs • Pairs induced background similar in both cases • Losses in extraction & background harder in 2 mrad but 2 mrad easier for detector Pairs induced backgriund in Si. D

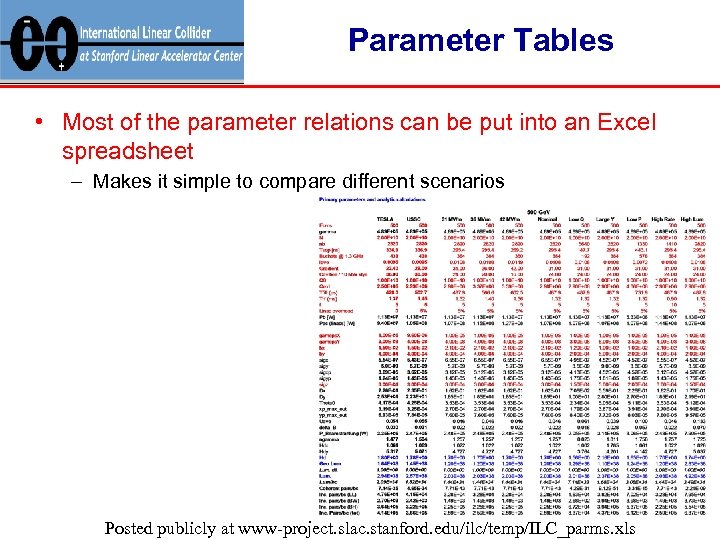Parameter Tables • Most of the parameter relations can be put into an Excel spreadsheet – Makes it simple to compare different scenarios Posted publicly at www-project. slac. stanford. edu/ilc/temp/ILC_parms. xls

Summary • Basic beam parameters are determined from the luminosity requirements – ILC design then follows trying to meet those requirements • Constrains arise from: – IP physics (luminosity, beamstrahlung, disruption, depth of focus) – Damping rings, bunch compressor and positron source – Rf acceleration – topic of Chris Adolphsen’s talk • Details will be discussed in all the subsequent talks – Looks like a great program! – Thanks to the organizers! • Join the ILC accelerator effort – an accelerator for the future