Linear Characteristics of Uniform and Accelerated Motion

Linear Characteristics of Uniform and Accelerated Motion

Linear Characteristics of Uniform and Accelerated Motion

Linear Characteristics of Uniform and Accelerated Motion

Methods of Description of Motion We can state the position of a material point in the space by position vector r starting at the reference point and ending at the point where the object is found at a given moment of time. We can specify the position of a material point at any moment of time by its position vector We are able to describe the change of the position of a moving object as time progresses by means of the displacement vector. This is the vector method of description of motion.

Methods of Description of Motion Often it is more convenient to deal not with r, but with Descartes (or orthogonal) coordinates designated as x, y, z. In this case one vector equation resolves into three scalar equations: This method of description of motion is known as coordinate method.

Motion of a Ball Projected Horizontally The movement of the ball may be represented as a superposition of two component motions: 1) uniform motion along the OX-axis, its equation is , and 2) uniformly accelerated motion along the OYaxis, its equation is. These two equations together form the kinematical equations of the motion of the ball. The trajectory of the object thrown forward with a horizontal velocity is a parabola.

Linear Characteristics of Uniform and Accelerated Motion: Speed and velocity Speed is a physical magnitude which shows what distance is covered by a steadily moving material point in a unit of time, Speed is a quantity which has no direction but only magnitude, it means that speed is a scalar. But the complete information is provided for this physical magnitude by stating its direction in addition to its magnitude. In this case we say ‘velocity’ instead of ‘speed’. The distinction between speed and velocity can be made clear by reference to a point moving uniformly round a circular track.

Velocity, average velocity, instantaneous velocity We shall define the velocity of an object moving steadily as the displacement per unit time: Many motions do not occur at constant velocity. If an object is moving non-uniformly, we shall deal with its average speed and average velocity : The velocity at a given instant is called the instantaneous velocity. We use the word ‘instantaneous’ to distinguish the velocity at one moment from the average velocity over an interval of time.

Speed is the first derivative of distance with respect to time The velocity at a particular instant is given by the limit of as ‘approaches zero’, that is, as gets smaller and smaller. Symbolically this statement is written (We read “lim” as “the limit as approaches 0 of…”). We make the interval shorter and shorter until ‘in the limit’, we get a definite result. This procedure lies at the heart of the branch of mathematics called the calculus. Using calculus notation, The speed is the first derivative of distance with respect to time.

Example Suppose an object moves and a relationship between the distance travelled by this object and the duration of time interval is given by equation where A, B, C are constants. We can find the velocity of this object at any moment of time by differentiating S with respect to t: Another example: we know how velocity of the moving object depends on time, let it be. We want to know the distance this object travels during the time interval :

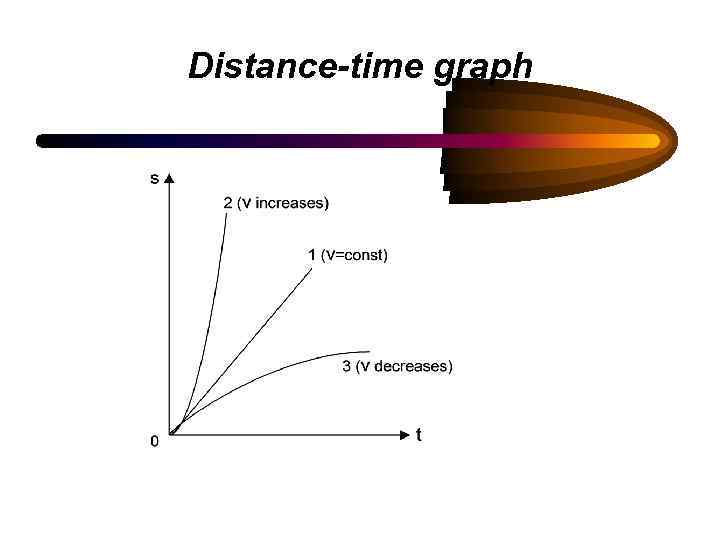Distance-time graph

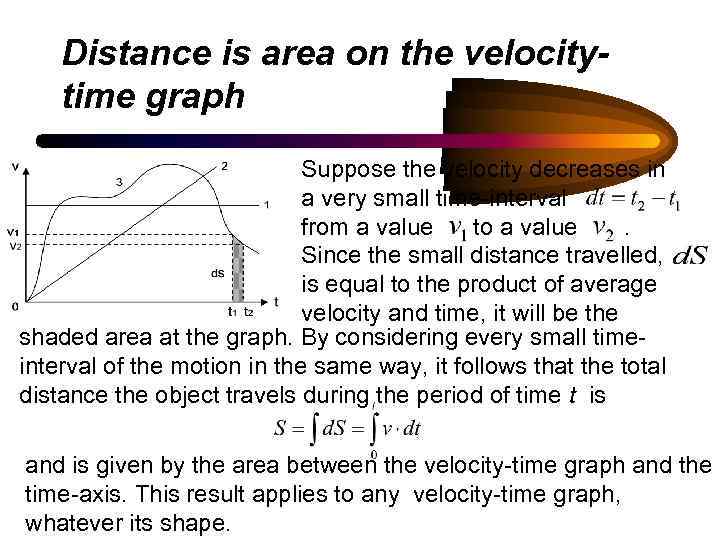Distance is area on the velocitytime graph Suppose the velocity decreases in a very small time-interval from a value to a value. Since the small distance travelled, is equal to the product of average velocity and time, it will be the shaded area at the graph. By considering every small timeinterval of the motion in the same way, it follows that the total distance the object travels during the period of time t is and is given by the area between the velocity-time graph and the time-axis. This result applies to any velocity-time graph, whatever its shape.

Acceleleration In case of non-uniform motion the velocity of the moving object changes. The acceleration of a moving object at an instant is the rate of change of its velocity at that instant. If the velocity changes by equal amounts in equal times, no matter how small the time-intervals may be, the acceleration is said to be uniform, and the motion to be uniformly accelerated motion. this is the average acceleration for a time interval.

Acceleration is the first derivative of velocity with respect to time To find the instantaneous acceleration at any particular time The acceleration is the first derivative of velocity with respect to time.

Uniform circular motion The velocity is different from the velocity , although their magnitudes are both equal to. The acceleration exists and is called centripetal (center-seeking) acceleration, . This acceleration is given by here n is a unit vector directed along the radius towards the center and is an angular speed of an object.

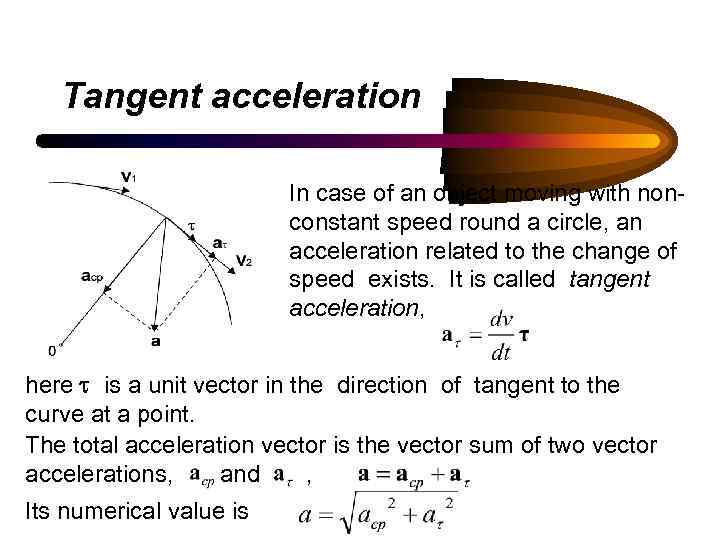Tangent acceleration In case of an object moving with nonconstant speed round a circle, an acceleration related to the change of speed exists. It is called tangent acceleration, here is a unit vector in the direction of tangent to the curve at a point. The total acceleration vector is the vector sum of two vector accelerations, and , Its numerical value is